Topics in Statistic Mechanics
Topics in Statistic Mechanics
Topics in Statistic Mechanics
You also want an ePaper? Increase the reach of your titles
YUMPU automatically turns print PDFs into web optimized ePapers that Google loves.
Adv. Sta. Phy. Homework 2 Blume-Capel Model Li,Zimeng PB06203182<br />
vanished at<br />
or<br />
[2] Blume-Capel Model<br />
The Blume-Capel model is different from [1] <strong>in</strong> its additional term<br />
, which allows<br />
the coefficient of <strong>in</strong> the free energy to change sign.Therefore the coefficient of<br />
may happen to be negative, and so the above diversity of free energy with respect to M<br />
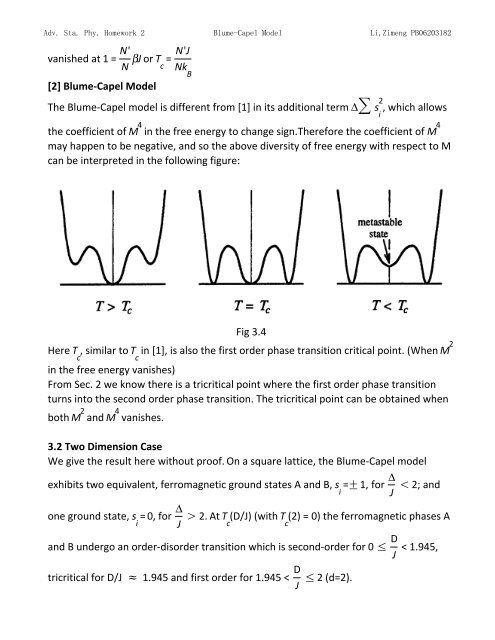
can be <strong>in</strong>terpreted <strong>in</strong> the follow<strong>in</strong>g figure:<br />
Here , similar to<br />
Fig 3.4<br />
<strong>in</strong> [1], is also the first order phase transition critical po<strong>in</strong>t. (When<br />
<strong>in</strong> the free energy vanishes)<br />
From Sec. 2 we know there is a tricritical po<strong>in</strong>t where the first order phase transition<br />
turns <strong>in</strong>to the second order phase transition. The tricritical po<strong>in</strong>t can be obta<strong>in</strong>ed when<br />
both and vanishes.<br />
3.2 Two Dimension Case<br />
We give the result here without proof. On a square lattice, the Blume-Capel model<br />
exhibits two equivalent, ferromagnetic ground states A and B, for ; and<br />
one ground state, , for . At (D/J) (with (2) = 0) the ferromagnetic phases A<br />
and B undergo an order-disorder transition which is second-order for < 1.945,<br />
tricritical for D/J 1.945 and first order for 1.945 < (d=2).