Pg 225
Pg 225
Pg 225
Create successful ePaper yourself
Turn your PDF publications into a flip-book with our unique Google optimized e-Paper software.
3.6 Finding Some Shortcuts —<br />
The Sum and Difference Rules<br />
SETTING THE STAGE<br />
A cliff diver in Acapulco, Mexico, dives from about 17 m above the water.<br />
The function f (t) 4.9t 2 1.5t 17 models the diver’s height above the<br />
water, in metres, at t seconds. Determine the diver’s instantaneous rate of<br />
descent with respect to time at intervals of 0.1 s during the first second the diver<br />
is in the air.<br />
The instantaneous rate of change of height is given by the derivative of the<br />
height function. Can the differentiation rules from the previous section be<br />
applied to the polynomial function that models the diver’s height?<br />
In this section we will develop the rules to differentiate any polynomial<br />
function.<br />
EXAMINING THE CONCEPT<br />
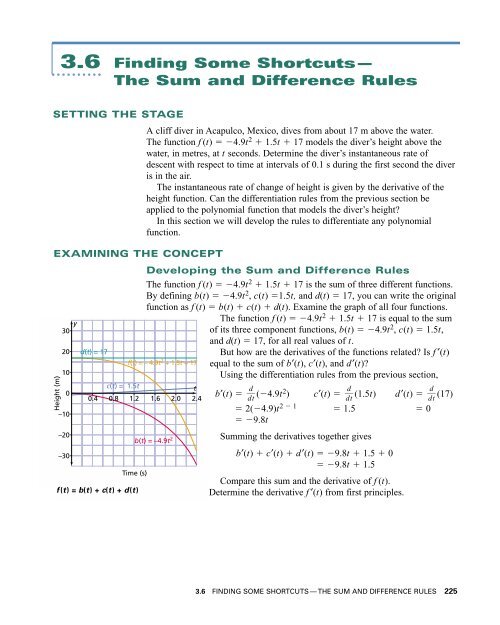
Height (m)<br />
y<br />
30<br />
20<br />
10<br />
0<br />
–10<br />
–20<br />
–30<br />
d(t) = 17<br />
c(t) = 1.5t<br />
Developing the Sum and Difference Rules<br />
The function f (t) 4.9t 2 1.5t 17 is the sum of three different functions.<br />
By defining b(t) 4.9t 2 , c(t) 1.5t, and d(t) 17, you can write the original<br />
function as f (t) b(t) c(t) d(t). Examine the graph of all four functions.<br />
The function f (t) 4.9t 2 1.5t 17 is equal to the sum<br />
of its three component functions, b(t) 4.9t 2 , c(t) 1.5t,<br />
and d(t) 17, for all real values of t.<br />
But how are the derivatives of the functions related? Is f ′(t)<br />
equal to the sum of b′(t), c′(t), and d′(t)?<br />
Using the differentiation rules from the previous section,<br />
f(t) = – 4.9t 2 + 1.5t + 17<br />
0.4 0.8 1.2 1.6 2.0 2.4<br />
Time (s)<br />
f (t) =b(t) +c(t) +d(t)<br />
b(t) = –4.9t 2<br />
t<br />
d<br />
b′(t) (4.9t 2 dt<br />
) c′(t) dt<br />
(1.5t) d′(t) dt<br />
(17)<br />
2(4.9)t 2 1 1.5 0<br />
9.8t<br />
Summing the derivatives together gives<br />
b′(t) c′(t) d′(t) 9.8t 1.5 0<br />
9.8t 1.5<br />
Compare this sum and the derivative of f (t).<br />
Determine the derivative f ′(t) from first principles.<br />
d<br />
d<br />
3.6 FINDING SOME SHORTCUTS — THE SUM AND DIFFERENCE RULES <strong>225</strong>
h(t) 4.9t 2 1.5t 17<br />
h′(t) lim<br />
h → 0<br />
lim<br />
h → 0<br />
lim<br />
h → 0<br />
lim<br />
h → 0<br />
lim<br />
h → 0<br />
lim<br />
h → 0<br />
lim<br />
f (t h) f (t)<br />
<br />
h<br />
[4.9(t h) 2 1.5(t h) 17] [4.9t 2 1.5t 17]<br />
<br />
h<br />
4.9(t 2 2th h 2 ) 1.5(t h) 17 [4.9t 2 1.5t 17]<br />
<br />
h<br />
4.9t 2 9.8th 4.9h 2 1.5t 1.5h 17 4.9t 2 1.5t 17<br />
<br />
h<br />
9.8th 4.9h 2 1.5h<br />
<br />
h<br />
h 1 (9.8t 4.9h 1.5)<br />
<br />
h<br />
1<br />
20.0<br />
(9.8t 4.9h 1.5) 10.0<br />
h → 0<br />
c′(t) = 1.5t<br />
0.0<br />
d′(t) = 0<br />
9.8t 4.9(0) 1.5<br />
9.8t 1.5<br />
The derivative of the original<br />
function, f (t), is the sum of the<br />
derivatives of the component<br />
functions, b(t), c(t), and d(t).<br />
f (t) b(t) c(t) d(t)<br />
4.9t 2 1.5t 17<br />
f ′(t) b′(t) c′(t) d′(t)<br />
9.8t 1.5<br />
Value of Derivative<br />
–10.0<br />
–20.0<br />
–30.0<br />
0.4 0.8 1.2 1.6 2.0 2.4<br />
Time (s)<br />
f ′(t) = b′(t) + c′(t) + d′(t)<br />
f′(t) = b′(t) + c′(t) + d′(t)<br />
= –9.8t + 1.5<br />
b′(t) = – 9.8t<br />
The derivative of a sum is<br />
the sum of the derivatives.<br />
The Sum Rule<br />
If h(x) f (x) g(x) and f and g are both differentiable, then<br />
h′(x) f ′(x) g′(x). In Leibniz notation,<br />
d<br />
d<br />
[ f (x) g(x)] d<br />
[ f (x)] d<br />
[g(x)].<br />
d<br />
d<br />
x<br />
x<br />
x<br />
Proof<br />
Let F(x) f(x) g(x).<br />
h ′(x) lim<br />
h → 0<br />
lim<br />
h → 0<br />
lim<br />
h → 0<br />
F(x h) F(x)<br />
h<br />
f (x h) f (x)<br />
h<br />
lim<br />
h → 0<br />
f ′(x) g′(x)<br />
[ f (x h) g(x h)] [ f (x) g(x)]<br />
<br />
h<br />
[f (x h) f (x)] [g(x h) g(x)]<br />
<br />
h<br />
lim<br />
h → 0<br />
g(x h) g(x)<br />
h<br />
Rearrange the numerator.<br />
Rewrite using the<br />
sum rule for limits.<br />
226 CHAPTER 3 RATES OF CHANGE IN POLYNOMIAL FUNCTION MODELS
The sum rule can be extended to any number of functions. A corresponding rule<br />
also exists for differences.<br />
The derivative of a<br />
difference is the difference<br />
of the derivatives.<br />
The Difference Rule<br />
If h(x) f (x) g(x) and f and g are both differentiable, then<br />
h′(x) f ′(x) g′(x). In Leibniz notation,<br />
d<br />
d<br />
[ f (x) g(x)] d<br />
[ f (x)] d<br />
[g(x)].<br />
d<br />
d<br />
x<br />
x<br />
x<br />
The proof for the difference rule is similar to the proof for the sum rule.<br />
Example 1<br />
Using the Sum and Difference Rules<br />
Determine the derivative of each function.<br />
(a) g(x) 8x 4 6x 2 12<br />
(b) h(x) 4x 2 5x 2 4x<br />
Solution<br />
Use the sum and difference rules. Differentiate term by term.<br />
d<br />
(a) g′(x) d<br />
(8x<br />
x<br />
4 6x 2 12)<br />
d<br />
d<br />
(8x<br />
x<br />
4 d<br />
) d<br />
(6x<br />
x<br />
2 d<br />
) d<br />
(12)<br />
x<br />
32x 3 12x 0<br />
32x 3 12x<br />
d<br />
(b) h′(x) d<br />
(4x<br />
x<br />
2 5x 2 4x)<br />
d<br />
d<br />
(4x<br />
x<br />
2 d<br />
) d<br />
(5x<br />
x<br />
2 d<br />
) d<br />
(4x)<br />
x<br />
8x 3 10x 4<br />
A polynomial function is a<br />
sum of functions in the<br />
form ax k , where k ∈ N. To<br />
find the derivative of any<br />
polynomial function, add<br />
the derivatives of the<br />
individual terms.<br />
Example 2<br />
The Derivative of Any Polynomial Function<br />
For any polynomial function,<br />
P(x) a n<br />
x n a n 1<br />
x n 1 … a 2<br />
x 2 a 1<br />
x 1 a 0<br />
, where n ∈ N,<br />
P′(x) na n<br />
x n 1 (n 1)a n 1<br />
x n 2 … 2a 2<br />
x 1 a 1<br />
.<br />
Determining the Derivative of a Polynomial Function<br />
Differentiate y 5x 4 2x 3 6x 2 9x 18.<br />
Solution<br />
d y d<br />
<br />
dx<br />
d x<br />
d<br />
d x<br />
(5x 4 2x 3 6x 2 9x 18)<br />
(5x 4 d<br />
) d<br />
(2x 3 d<br />
) d<br />
(6x 2 d d<br />
) d<br />
(9x) d<br />
(18)<br />
20x 3 6x 2 12x 9 0<br />
20x 3 6x 2 12x 9<br />
x<br />
x<br />
3.6 FINDING SOME SHORTCUTS — THE SUM AND DIFFERENCE RULES 227<br />
x<br />
x
Example 3<br />
Using the Sum and Difference Rules to Determine an<br />
Instantaneous Rate of Change<br />
Recall the problem in Setting the Stage.<br />
A cliff diver in Acapulco, Mexico, dives from about 17 m above the water.<br />
The function f (t) 4.9t 2 1.5t 17 models the diver’s height above the<br />
water, in metres, at t seconds. Determine the diver’s instantaneous rate of<br />
descent with respect to time at intervals of 0.1 s during the first second the diver<br />
is in the air.<br />
Solution<br />
Given f (t), which is the height at time t, the instantaneous rate of change of<br />
height with respect to time — the rate of descent — is f ′(t). In this case,<br />
d<br />
f ′(t) d<br />
(4.9t<br />
t<br />
2 1.5t 17)<br />
9.8t 1.5<br />
The table shows the rate of descent every 0.1 s during the first second.<br />
Time, t (s) 0.0 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9 1.0<br />
Instantaneous<br />
Rate of Descent, 1.5 0.5 –0.5 –1.4 –2.4 –3.4 –4.4 –5.4 –6.3 –7.3 –8.3<br />
f ′(t) = –9.8t + 1.5 (m/s)<br />
A positive rate means the diver is moving up. A negative rate means the diver is<br />
moving down. The rate is initially positive because the diver jumps up off the<br />
cliff. Between 0.1 s and 0.2 s, the diver starts to fall, and the pull of gravity<br />
steadily increases the rate of descent until the diver enters the water.<br />
Height (m)<br />
f(t)<br />
18<br />
16<br />
f(t) = – 4.9t 2 + 1.5t + 17<br />
14<br />
12<br />
10<br />
8<br />
6<br />
4<br />
2<br />
t<br />
0 1 2 3 4<br />
Time (s)<br />
Rate of Descent (m/s)<br />
8.0<br />
4.0<br />
0.0<br />
–4.0<br />
–8.0<br />
–12.0<br />
–16.0<br />
–20.0<br />
f′(t)<br />
t<br />
0.5 1 1.5 2 2.5<br />
f′(t) = – 9.8t + 1.5<br />
Time (s)<br />
Diver’s rate of descent versus time<br />
Diver’s height versus time<br />
228 CHAPTER 3 RATES OF CHANGE IN POLYNOMIAL FUNCTION MODELS
CHECK, CONSOLIDATE, COMMUNICATE<br />
d<br />
1. Show graphically that d<br />
(x<br />
x<br />
2 d<br />
2x) d<br />
(x<br />
x<br />
2 d<br />
) d<br />
(2x).<br />
x<br />
2. If h(x) g(x) f (x), where g(x) 4x 3 and f (x) 5x 2 , does<br />
h′(2) g′(2) f ′(2)? Explain.<br />
3. Explain why any polynomial function can be differentiated term by term.<br />
KEY IDEAS<br />
The table summarizes the differentiation rules developed in this section.<br />
Rule Function Notation Leibniz Notation<br />
d<br />
d<br />
d<br />
Sum Rule If h(x) = f (x) + g(x) and d<br />
[f (x) + g(x)] = <br />
x<br />
d<br />
[f (x)] + <br />
x d<br />
[g(x)]<br />
x<br />
f and g are both<br />
differentiable, then<br />
h′(x) = f ′(x) + g′(x).<br />
d<br />
d<br />
d<br />
Difference If h(x) = f (x) – g(x) and d<br />
[f (x) – g(x)] = <br />
x<br />
d<br />
[f (x)] – <br />
x d<br />
[g(x)]<br />
x<br />
Rule f and g are both<br />
differentiable, then<br />
h′(x) = f ′(x) – g′(x).<br />
Derivative of If P(x) = a n<br />
x n + a n – 1<br />
x n – 1 + … + a 2<br />
x 2 + a 1<br />
x 1 + a 0<br />
, where n ∈ N,<br />
a Polynomial then P′(x) = na n<br />
x n – 1 + (n – 1)a n – 1<br />
x n – 2 + … + 2a 2<br />
x 1 + a 1<br />
.<br />
3.6 Exercises<br />
A<br />
1. For y 3x 2 2x 1,<br />
(a) find d y<br />
from first principles<br />
dx<br />
(b) confirm your results for (a) using the rules for differentiation<br />
2. Differentiate.<br />
(a) y 4x 2 5x 2 (b) y x 3 5x 2 2x 8<br />
(c) y 3x 2 (d) y 4x 2 5x 1<br />
(e) f (x) 8x 3 (f) f (x) 3x 2 2x 5<br />
3<br />
(g) f (x) x 4 2 x 5 (h) f (x) 6x4 3x 3 9x 2 5x 8<br />
3. Determine the slope of the tangent line at the given point for each function.<br />
(a) y 3x 5 at (2, 11) (b) y 4x 2 3x 7 at (1, 14)<br />
(c) y 2x 3 at (2, 16)<br />
(d) y 5x 4 4x 3 3x 2 6x 2 at (0, 2)<br />
(e) y 5x 2 6x 3 at (0, 3) (f) y 7x 4 x 2 6x at (1, 2)<br />
3.6 FINDING SOME SHORTCUTS — THE SUM AND DIFFERENCE RULES 229
B<br />
4. (a) Find the equation of the tangent to the curve of y 2x 2 5x 7<br />
where x 1.<br />
(b) Draw a sketch of the function and the tangent.<br />
5. Communication: Express in your own words the sum and difference rules<br />
for differentiation. Use an example to illustrate each rule.<br />
6. Knowledge and Understanding: Determine d for the function<br />
dx<br />
y 5x 4 8x 3 3x 2 6x 9.<br />
7. Determine the equation of the tangent to the curve of y x 2 3x 1 at<br />
each point.<br />
(a) (1, 5) (b) (2, 11) (c) (0, 1) (d) 1 2 , 1 4 <br />
8. For f (x) 3x 2 8x 5 and g(x) 5x 3 4x 2 5x 7, show that<br />
(a) the derivative of the sum equals the sum of the derivatives<br />
(b) the derivative of the difference equals the difference between the<br />
derivatives<br />
9. Find the equation of the tangent to each curve.<br />
(a) y x 2 5x 4 where x 3<br />
(b) y 4x 2 x 5 where x 1 2 <br />
(c) f (x) x 3 5x 2 6x 7 where x 1<br />
(d) f (x) 5x 4 x 3 6x where x 3<br />
10. Find the equations of all the tangents to the graph of f (x) x 2 4x 25<br />
that pass through the origin.<br />
11. Application: Liquid is flowing out of a tank. The volume, V, in litres<br />
remaining after t minutes is given by V(t) 1000(20 t 2 ).<br />
(a) What is the initial volume of liquid in the tank?<br />
(b) Over the first two minutes, what is the average rate at which the tank is<br />
being emptied?<br />
(c) At exactly what time is this rate in effect?<br />
(d) How fast is the liquid leaving the tank at 3 min?<br />
(e) How long, to the nearest half minute, will the liquid take to drain<br />
completely from the tank?<br />
(f) What is the average rate, to the nearest litre per minute, at which the<br />
liquid drains?<br />
12. A business report determines that a company’s profit, P, in dollars per<br />
month can be expressed as a function of the number of items<br />
manufactured, x:<br />
P(x) x 3 32x 2 560x 9600, 0 ≤ x ≤ 40<br />
(a) Explain why the y-intercept of the graph is negative.<br />
y<br />
230 CHAPTER 3 RATES OF CHANGE IN POLYNOMIAL FUNCTION MODELS
(b) At what rate is the profit changing when 15 items are manufactured?<br />
35? 26?<br />
(c) What is the profit when 15 items are manufactured? 35? 26?<br />
(d) For what levels of production is the company profitable?<br />
13. Kathy has diabetes. Her blood sugar level, B, one hour after an insulin<br />
injection, depends on the amount of insulin, x, in milligrams injected.<br />
B(x) 0.2x 2 500, 0 ≤ x ≤ 40<br />
(a) Find B(0) and B(30).<br />
(b) Find B′(0) and B′(30).<br />
(c) Interpret your results.<br />
(d) Consider the values of B′(50) and B(50). Comment on the significance<br />
of these values. Why are restrictions given for the original function?<br />
14. (a) Find coordinates of the points, if any, where each function has a<br />
horizontal tangent line.<br />
i. f (x) 2x 5x 2<br />
ii. f (x) 4x 2 2x 3<br />
iii. f (x) x 3 8x 2 5x 3<br />
(b) Suggest a graphical interpretation for each of these points.<br />
15. Thinking, Inquiry, Problem Solving: Find numbers a, b, and c so that the<br />
graph of f (x) ax 2 bx c has x-intercepts at (0, 0) and (8, 0), and a<br />
tangent with slope 16 where x 2.<br />
16. The population, P, of a bacteria colony at t hours can be modelled by<br />
P(t) 100 120t 10t 2 2t 3<br />
(a) What is the initial population of the bacteria colony?<br />
(b) What is the population of the colony at 5 h?<br />
(c) What is the growth rate of the colony at 5 h?<br />
17. Coffee consumption in the United States can be modelled by<br />
C(x) 2.767 75 0.084 794 3x 0.008 320 58x 2 0.000 144 017x 3 ,<br />
where C represents the number of cups consumed per day by the average<br />
adult and x represents the number of years since 1955.<br />
(a) How many cups of coffee did the average American adult consume each<br />
day in 2000?<br />
(b) What was the rate of change in the number of cups of coffee consumed<br />
per adult per day in 2000?<br />
18. Check Your Understanding<br />
(a) Determine f ′(3), where f (x) 6x 3 4x 5x 2 10.<br />
(b) Give two interpretations of the meaning of f ′(3).<br />
3.6 FINDING SOME SHORTCUTS — THE SUM AND DIFFERENCE RULES 231
C<br />
19. Prove that the tangent to the curve y x 2x 2 x 4 at point (1, 0) is<br />
also tangent to the curve at (1, 2).<br />
20. For any point (x, y) on the graph of y 3x 2 15x 3, determine the<br />
coordinates of the point on y 2x 2 5x 4 such that the tangents at the<br />
two points are parallel.<br />
21. Show that f (x) 8x 3 7x 5 has no tangent line with slope 5.<br />
22. Show that the x- and y-intercepts for any tangent to the curve<br />
y 16 8x x have a sum of 16.<br />
ADDITIONAL ACHIEVEMENT CHART QUESTIONS<br />
Knowledge and Understanding: Consider the function f (x) x 4 7x 12.<br />
(a) Write the equation of the tangent line at x 1.<br />
(b) Find the coordinates of the point on the function so that the tangent line is<br />
perpendicular to x 25y 175 0.<br />
Application: An ant colony was treated with an insecticide and the number of<br />
survivors, A, in hundreds at t hours is A(t) t 3 5t 750.<br />
(a) Find A′(t).<br />
(b) Find the rate of change of the number of living ants in the colony at 10 h.<br />
(c) How many ants were in the colony before it was treated with the insecticide?<br />
(d) How many hours after the insecticide was applied were no ants remaining in<br />
the colony?<br />
Thinking, Inquiry, Problem Solving: Suppose that f (x) is a quadratic polynomial<br />
function. Where would you find a horizontal tangent line? a vertical tangent<br />
line?<br />
Communication: You are writing a self-help manual in calculus. Write the steps<br />
for helping readers find the equation of the line that is tangent to the graph of<br />
g(x) x 4 2x 3 5x 2 where x 2. Explain each step.<br />
The Chapter Problem<br />
Average Salaries in Professional Sports<br />
Apply what you learned to answer this question about The Chapter<br />
Problem on page 168.<br />
CP9.<br />
Use the cubic regression equations you created for question CP7.<br />
Then apply the differentiation rules to verify the derivatives you<br />
found for question CP7.<br />
232 CHAPTER 3 RATES OF CHANGE IN POLYNOMIAL FUNCTION MODELS
3.7 Polynomial Function Models<br />
and the First Derivative<br />
SETTING THE STAGE<br />
EXAMINING THE CONCEPT<br />
Displacement<br />
f(t)<br />
secant<br />
s = f(t)<br />
tangent<br />
Time (s)<br />
Displacement versus time<br />
This chapter has discussed using the derivative to determine the instantaneous<br />
rate of change of a quantity. The derivative has wide application in fields such as<br />
economics, science, engineering, and the social sciences. Here is an example:<br />
Suppose a rock is thrown into the air from a bridge 15 m above the water.<br />
As it rises and then falls, its height above the water is a function of the time<br />
since it was thrown. The height of the rock, in metres, above the water at<br />
t seconds can be modelled by the function h(t) 4.9t 2 12t 15.<br />
What is the velocity of the rock when it enters the water?<br />
In this section we will examine applications of the first derivative of a<br />
polynomial model.<br />
Polynomial Models Involving Velocity and Speed<br />
In many situations, an object’s position, s, can be described by a<br />
function of time, s f (t). Average velocity is defined as the rate of<br />
change of displacement over an interval of time. Instantaneous velocity<br />
is the rate of change of displacement at a specific point in time.<br />
On a displacement-time graph, the slope of a secant represents<br />
average velocity, while the slope of a tangent represents instantaneous<br />
velocity.<br />
t<br />
average velocity ∆ <br />
∆t<br />
instantaneous velocity lim<br />
s<br />
∆ <br />
s<br />
∆t → 0 ∆t<br />
lim<br />
∆t → 0<br />
lim<br />
h → 0<br />
f ′(t)<br />
As a result, the derivative of the position function, s′ f ′(t), represents the<br />
instantaneous velocity of the object at time t. So<br />
s<br />
v(t) d <br />
dt<br />
s′<br />
f ′(t)<br />
f (t ∆t) f (t)<br />
∆t<br />
f (t h) f (t)<br />
h<br />
3.7 POLYNOMIAL FUNCTION MODELS AND THE FIRST DERIVATIVE 233