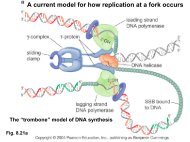
3. Basic probability concepts

More documents

Recommendations

Info

Mutually exclusive events In probability theory, a set of events { E E E } 1, 2, K , n are said to be mutually exclusive if the occurrence of any one of them automatically implies the non-occurrence of the remaining n − 1 events. In other words, two mutually exclusive events cannot both occur; at most one of the events can occur. The events comprising a sample space are mutually exclusive. A related concept is that of being collectively exhaustive, which means that at least one of the events must occur. Probability concepts Probabilities are always expressed as fractional or decimal values, but there are important distinctions in how those values are obtained. For simple events, probabilities may be derived classically based on the concept of fairness, may be observed empirically, or may be assigned subjectively. These distinctions have important implications for statistical analyses. Classical probabilities Some events are defined so narrowly that the probabilities of their outcomes can be deduced logically. The simplest such case involves a sample space having a finite set of discrete events, with each event having the same probability. Such probabilities can be called classical probabilities. Few scientific situations are of this sort, but the derivation of classical probabilities is worth examining because the predictability of simple processes may provide insight into the more complicated situations that are so common in science. Throwing dice is one of man’s oldest known probabilistic endeavors. Because it is a cube, a modern die has six labeled faces and so a single throw of the die results in a face value from 1 to 6. The sample space is thus S = { 1, 2, 3, 4, 5, 6} . What is the probability of obtaining, say, a 5 If all face values are equally likely to occur, then a 5 is one possible outcome out of six, and its probability is therefore 1/6, or approximately 0.17. Note that to assign this probability we need to assume that all face values are equally likely to occur. This is the strong assumption of fairness, and in the case of a die is unlikely to be strictly true because of inhomogeneities in the material of the die. However, it may be true enough for practical purposes, sufficiently true that we are willing to live with the assumption that the die is fair. If we define an event to be the throwing of two dice, then there are more possible outcomes. Considering only the sum of the face values, there are 11 possible outcomes: 2 through 12. A naïve dice player might assume that these 11 events are all equally likely; however, a craps player who believed this would probably loose a lot of money. The probability of obtaining a 5, for example, is not simply 1/11 (approximately 0.09) because there are a number of different ways that this outcome can be generated. The throwing of two dice is a compound event, and the possible outcomes (sums) are shown in the following table. 4
Value of first die Value of second die 1 2 3 4 5 6 1 2 3 4 5 6 7 2 3 4 5 6 7 8 3 4 5 6 7 8 9 4 5 6 7 8 9 10 5 6 7 8 9 10 11 6 7 8 9 10 11 12 The table shows that there are 36 possible outcomes, four of which result in a sum of 5 for the two dice. If the dice are fair then all 36 outcomes are equally likely to occur, and the probability of a 5 on one throw of two fair die is 4/36, or approximately 0.11. The most likely outcomes from throwing two dice simultaneously are sums of either 6 or 7; both outcomes have probabilities of 6/36 = 1/6, or approximately 0.17. Since there is only one way to throw a sum of 12 (=6+6), its probability is 1/36, or approximately 0.03. These examples suggest a general definition for classical probability: The classical probability of an outcome is the number of ways that outcome can occur, relative to the total number of ways that all outcomes of an event can be generated. Or, more concisely, Pr ( outcome) number of ways outcome can occur = number of ways all outcomes can occur where Pr( outcome ) is read as “the probability of the outcome”. If we call a particular outcome A, this can be written as nA ( ) Pr( A) = . n The most common use of classical probabilities in statistics is to serve as null hypotheses. For example, when we flip a fair coin, the probability of observing a head is the same as the probability of a tail; both are ½. If we have reason to believe that the coin is not fair, the assumption of fairness is translated into a null hypothesis of equal probability, which can then be tested using empirical probabilities (described in the following section). In an ecological study of predator behavior in which the predator has four potential prey species, an initial and simplistic null hypothesis might be that the prey species are equally likely to be selected by the predator, each with a probability of ¼. This can be tested using empirical probabilities. Empirical probabilities Empirical probabilities are values derived by sampling, and are based on the concept of long-run or asymptotic relative frequency. The relative frequency of a particular outcome is the 5
Page 1 and 2: From: R.E. Strauss, Statistical Hyp
Page 3: (observations or entities) from an
Page 7 and 8: frequency (and thus estimated proba
Page 9: subjective probabilities should be

3. Basic probability concepts

You also want an ePaper? Increase the reach of your titles

Delete template?

Save as template?