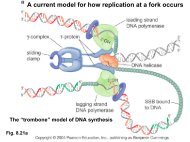
3. Basic probability concepts

frequency (and thus estimated probability) of the outcome will then be biased, but we will be
unaware of the nature and extent of the bias. Minimizing bias is one of the main objectives of
sampling theory.
The classical and empirical definitions of probability are basically identical, but because the
total number of potential observations can be large, the terminology is modified slightly:
The empirical probability of an outcome is observed frequency of that outcome, relative
to the total number of observations.
Pr ( outcome)
observed frequency
=
total frequency
nA ( )
Pr( A)
=
n
The variable n in the case represents the number of observations rather than the number of
distinct outcomes. For obvious reasons this is known as the frequency (or frequentist) definition
of probability. As a definition, it is equally valid no matter what the observed and total
frequencies. However, as an estimate of some “true” population frequency, it is more precise for
larger than for smaller total frequencies.
For example, say that we are trying to estimate the sex ratio of a (biological) population of
field mice living in a particular large field, which we define to be our statistical population. The
sex ratio (expressed in this case as the ratio of males to total number of individuals) can be
viewed as the probability of randomly drawing a male from the population, assuming that all
individuals are equally likely to be caught. (Is this a reasonable assumption) We might
estimate this probability by sampling 10 individuals from the population and discovering that 6
are males, giving Pr( male ) = 6 /10 = 0.6 . Or we might sample 1000 individuals and discover
that 513 are males, giving Pr( male ) = 513/1000 = 0.513 . It is reasonable to conclude that the
second estimate is somehow better than the first, because it is larger. We will show later (when
discussing confidence intervals) in what sense the second estimate is better than the first.
One potential use of empirical probabilities is to test null hypotheses that specify explicit
values for population parameters. For example, our null hypothesis might be that the population
of field mice consists of half females and half males – i.e., that the probabilities of randomly
drawing a female or drawing a male from the population are both ½. We might posit these
probabilities simply because there are two classes of individuals, which are assumed to be
equally likely (the classical frequencies). Or, if we are more informed, we might posit the
probabilities because Fisher’s (1930) sex-ratio model predicts for most populations a stable
equilibrium with equal numbers of females and males. In either case, the null-hypothesis values
of ½ and ½ can be tested by randomly sampling individuals from the population and determining
the relative frequencies, which are then used as estimates of probabilities to compare against the
null-hypothesis values. This raises the issue of just how different the observed frequencies have
to be from the postulated values to reject the null hypothesis. We will return to this example
when discussing statistical tests of hypotheses.
7