Statistical thermodynamics 1: the concepts - W.H. Freeman
Statistical thermodynamics 1: the concepts - W.H. Freeman
Statistical thermodynamics 1: the concepts - W.H. Freeman
Create successful ePaper yourself
Turn your PDF publications into a flip-book with our unique Google optimized e-Paper software.
PC8eC16 1/26/06 14:34 Page 576<br />
576 16 STATISTICAL THERMODYNAMICS 1: THE CONCEPTS<br />
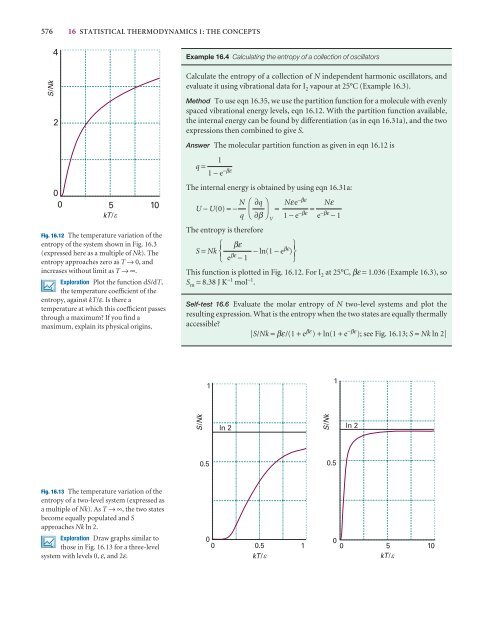
SNk /<br />
4<br />
2<br />
0<br />
0 5 10<br />
kT/<br />
Fig. 16.12 The temperature variation of <strong>the</strong><br />
entropy of <strong>the</strong> system shown in Fig. 16.3<br />
(expressed here as a multiple of Nk). The<br />
entropy approaches zero as T → 0, and<br />
increases without limit as T →∞.<br />
Exploration Plot <strong>the</strong> function dS/dT,<br />
<strong>the</strong> temperature coefficient of <strong>the</strong><br />
entropy, against kT/ε. Is <strong>the</strong>re a<br />
temperature at which this coefficient passes<br />
through a maximum If you find a<br />
maximum, explain its physical origins.<br />
Example 16.4 Calculating <strong>the</strong> entropy of a collection of oscillators<br />
Calculate <strong>the</strong> entropy of a collection of N independent harmonic oscillators, and<br />
evaluate it using vibrational data for I 2 vapour at 25°C (Example 16.3).<br />
Method To use eqn 16.35, we use <strong>the</strong> partition function for a molecule with evenly<br />
spaced vibrational energy levels, eqn 16.12. With <strong>the</strong> partition function available,<br />
<strong>the</strong> internal energy can be found by differentiation (as in eqn 16.31a), and <strong>the</strong> two<br />
expressions <strong>the</strong>n combined to give S.<br />
Answer The molecular partition function as given in eqn 16.12 is<br />
1<br />
q =<br />
1 − e −βε<br />
The internal energy is obtained by using eqn 16.31a:<br />
N A ∂q D Nεe −βε Nε<br />
U − U(0) =− = =<br />
q C ∂β F<br />
V<br />
1 − e −βε e −βε − 1<br />
The entropy is <strong>the</strong>refore<br />
1 βε<br />
5<br />
S = Nk 2 − ln(1 − e βε ) 6<br />
3 e βε − 1<br />
7<br />
This function is plotted in Fig. 16.12. For I 2 at 25°C, βε = 1.036 (Example 16.3), so<br />
S m = 8.38 J K −1 mol −1 .<br />
Self-test 16.6 Evaluate <strong>the</strong> molar entropy of N two-level systems and plot <strong>the</strong><br />
resulting expression. What is <strong>the</strong> entropy when <strong>the</strong> two states are equally <strong>the</strong>rmally<br />
accessible<br />
[S/Nk = βε/(1 + e βε ) + ln(1 + e −βε ); see Fig. 16.13; S = Nk ln 2]<br />
1<br />
1<br />
SNk /<br />
ln 2<br />
SNk /<br />
ln 2<br />
0.5<br />
0.5<br />
Fig. 16.13 The temperature variation of <strong>the</strong><br />
entropy of a two-level system (expressed as<br />
a multiple of Nk). As T →∞, <strong>the</strong> two states<br />
become equally populated and S<br />
approaches Nk ln 2.<br />
Exploration Draw graphs similar to<br />
those in Fig. 16.13 for a three-level<br />
system with levels 0, ε, and 2ε.<br />
0<br />
0<br />
0.5<br />
kT/ <br />
1<br />
0<br />
0 5 10<br />
kT/