Ab Initio Calculations of Hydroxyl Impurities in CaF2

More documents

Recommendations

Info

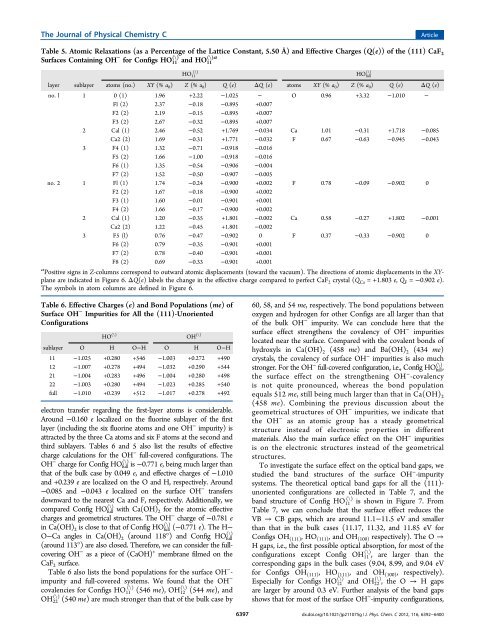
The Journal of Physical Chemistry CArticleTable 5. Atomic Relaxations (as a Percentage of the Lattice Constant, 5.50 Å) and Effective Charges (Q(e)) of the (111) CaF 2Surfaces Containing OH − for Configs HO (\) (\)a11 and HO 11HO 11(\)layer sublayer atoms (no.) XY (% a 0 ) Z (% a 0 ) Q (e) ΔQ (e) atoms XY (% a 0 ) Z (% a 0 ) Q (e) ΔQ (e)no. l 1 0 (1) 1.96 +2.22 −1.025 − O 0.96 +3.32 −1.010 −Fl (2) 2.37 −0.18 −0.895 +0.007F2 (2) 2.19 −0.15 −0.895 +0.007F3 (2) 2.67 −0.32 −0.895 +0.0072 Cal (1) 2.46 −0.52 +1.769 −0.034 Ca 1.01 −0.31 +1.718 −0.085Ca2 (2) 1.69 −0.31 +1.771 −0.032 F 0.67 −0.63 −0.945 −0.0433 F4 (1) 1.32 −0.71 −0.918 −0.016F5 (2) 1.66 −1.00 −0.918 −0.016F6 (1) 1.35 −0.54 −0.906 −0.004F7 (2) 1.52 −0.50 −0.907 −0.005no. 2 1 Fl (1) 1.74 −0.24 −0.900 +0.002 F 0.78 −0.09 −0.902 0F2 (2) 1.67 −0.18 −0.900 +0.002F3 (1) 1.60 −0.01 −0.901 +0.001F4 (2) 1.66 −0.17 −0.900 +0.0022 Cal (1) 1.20 −0.35 +1.801 −0.002 Ca 0.58 −0.27 +1.802 −0.001Ca2 (2) 1.22 −0.45 +1.801 −0.0023 F5 (l) 0.76 −0.47 −0.902 0 F 0.37 −0.33 −0.902 0F6 (2) 0.79 −0.35 −0.901 +0.001F7 (2) 0.78 −0.40 −0.901 +0.001F8 (2) 0.69 −0.33 −0.901 +0.001a Positive signs in Z-columns correspond to outward atomic displacements (toward the vacuum). The directions of atomic displacements in the XYplaneare indicated in Figure 6. ΔQ(e) labels the change in the effective charge compared to perfect CaF 2 crystal (Q Ca = +1.803 e, Q F = −0.902 e).The symbols in atom columns are defined in Figure 6.(\)HO fullTable 6. Effective Charges (e) and Bond Populations (me)ofSurface OH − Impurities for All the (111)-UnorientedConfigurationselectron transfer regarding the first-layer atoms is considerable.Around −0.160 e localized on the fluorine sublayer of the firstlayer (including the six fluorine atoms and one OH − impurity) isattracted by the three Ca atoms and six F atoms at the second andthird sublayers. Tables 6 and 5 also list the results of effectivecharge calculations for the OH − full-covered configurations. TheOH − charge for Config HO (\) full is −0.771 e, being much larger thanthat of the bulk case by 0.049 e, and effective charges of −1.010and +0.239 e are localized on the O and H, respectively. Around−0.085 and −0.043 e localized on the surface OH − transfersdownward to the nearest Ca and F, respectively. Additionally, wecompared Config HO (\) full with Ca(OH) 2 for the atomic effectivecharges and geometrical structures. The OH − charge of −0.781 ein Ca(OH) 2 is close to that of Config HO (\) full (−0.771 e). The H−(\)O−Ca angles in Ca(OH) 2 (around 118°) and Config HO full(around 113°) are also closed. Therefore, we can consider the fullcoveringOH − as a piece of (CaOH) + membrane filmed on theCaF 2 surface.Table 6 also lists the bond populations for the surface OH − -impurity and full-covered systems. We found that the OH −covalencies for Configs HO (\) 11 (546 me), OH (\) 12 (544 me), and(\) (540 me) are much stronger than that of the bulk case byOH 22HO (\) OH (\)sublayer O H O−H O H O−H11 −1.025 +0.280 +546 −1.003 +0.272 +49012 −1.007 +0.278 +494 −1.032 +0.290 +54421 −1.004 +0.283 +496 −1.004 +0.280 +49822 −1.003 +0.280 +494 −1.023 +0.285 +540full −1.010 +0.239 +512 −1.017 +0.278 +492639760, 58, and 54 me, respectively. The bond populations betweenoxygen and hydrogen for other Configs are all larger than thatof the bulk OH − impurity. We can conclude here that thesurface effect strengthens the covalency of OH − impuritieslocated near the surface. Compared with the covalent bonds ofhydroxyls in Ca(OH) 2 (458 me) and Ba(OH) 2 (434 me)crystals, the covalency of surface OH − impurities is also muchstronger. For the OH − full-covered configuration, i.e., Config HO (\) full ,the surface effect on the strengthening OH − -covalencyis not quite pronounced, whereas the bond populationequals 512 me, still being much larger than that in Ca(OH) 2(458 me). Combining the previous discussion about thegeometrical structures of OH − impurities,weindicatethatthe OH − as an atomic group has a steady geometricalstructure instead of electronic properties in differentmaterials. Also the main surface effect on the OH − impuritiesis on the electronic structures instead of the geometricalstructures.To investigate the surface effect on the optical band gaps, westudied the band structures of the surface OH − -impuritysystems. The theoretical optical band gaps for all the (111)-unoriented configurations are collected in Table 7, and theband structure of Config HO (\) 11 is shown in Figure 7. FromTable 7, we can conclude that the surface effect reduces theVB → CB gaps, which are around 11.1−11.5 eV and smallerthan that in the bulk cases (11.17, 11.32, and 11.85 eV forConfigs OH (111) ,HO (111) , and OH (100) respectively). The O →H gaps, i.e., the first possible optical absorption, for most of theconfigurations except Config OH (\) 11 , are larger than thecorresponding gaps in the bulk cases (9.04, 8.99, and 9.04 eVfor Configs OH (111) , HO (111) , and OH (100) , respectively).Especially for Configs HO (\) 12 and OH (\) 22 , the O → H gapsare larger by around 0.3 eV. Further analysis of the band gapsshows that for most of the surface OH − -impurity configurations,dx.doi.org/10.1021/jp211075g | J. Phys. Chem. C 2012, 116, 6392−6400
The Journal of Physical Chemistry CArticleTable 7. Direct Optical Band Gaps (eV) (Γ → Γ) of the Surface OH − for the 10 (111)-Unoriented Configurations(\) (\) (\) (\) (\) (\) (\) (\) (\) (\)gaps HO 11 HO 11 HO 12 HO 12 HO 21 HO 21 HO 22 HO 22 HO full HO fullO 1 → H 9.23 8.97 9.37 9.21 9.19 9.23 9.26 9.32 7.89 8.75O 2 → H 9.24 8.98 9.38 9.21 9.22 9.24 9.26 9.34 7.89 8.76O 1 → CB 9.79 9.46 9.77 9.86 9.76 9.96 9.88 10.06 9.36 9.83O 2 → CB 9.80 9.47 9.78 9.86 9.79 9.97 9.88 10.08 9.36 9.84VB → CB 11.31 11.09 11.0 11.36 11.08 11.16 11.08 11.46 11.10 11.32Figure 7. Calculated B3PW band structures for Configs HO (\) 11 (left)and HO (\) full (right).the occupied defect levels induced by O atoms move downwardaround 0.1−0.3 eV (toward VB) with respect to the bulk cases,leading to widening of the O → H gaps. From Figure 7, we alsofound that the empty defect band induced by H atoms is veryclose to the CB bottom and there is nearly no separated Hband, which almost superposes with the CB. Unlike the surfaceOH − -impurity systems, the O → H gaps for the OH − fullcoveredsystems are narrower than that of the bulk case byaround 1.1 and 0.3 eV for Configs HO (\) full and OH (\) full , respectively.Especially for Config HO (\) full ,theO→ H gap reduces to 7.89 eV,being much smaller than the relevant gap of 9.04 eV in the bulkcase. It is mainly due to the downward shift of the unoccupiedH band, which moves toward the O bands by around 1 eV, as wecanseeFigure7.To further study the electronic structure and electron transitionsin a surface OH − -impurity system, we calculated the DOSof Config HO (\) 11 , as we can see in Figure 8. Our previous bulkOH − -impurity study demonstrated that the O p orbitals formthe two superposed occupied O bands, i.e., so-called O bands,and the H s orbitals do the major contribution to the emptydefect band, named H band in the bulk case, below the CBbottom. In the 2D cases, the symmetry of p x ,p y , and p z states isbroken by the (111)-terminated surface; therefore, the p-stateelectrons are not equivalent in the three directions. Our DOScalculations show that the two superposed occupied O bandsmainly consist of O p x and p y orbitals.Because of the surface effect, the O p x and p y orbitals movedownward, toward the VB top, with respect to the O p orbitalsin the bulk cases, and this leads to narrowing of the VB → Ogaps and widening of the O → H gaps. As discussion above,there is no remarkably separated defect band induced by Hatoms located below the CB bottom, being in agreement withour DOS calculation on H atoms (see Figure 8).Figure 8. Total and projected DOS for Config HO 11 (\) .C. Formation of OH − Impurities. Finally, we studied theformation of OH − impurities in CaF 2 . We computed theformation energy of the OH − impurity in CaF 2 crystal. In thesupercell calculation for an isolated OH − , the formation energyof a neutral (the charge of total supercell is neutral) OH −impurity in CaF 2 could be expressed as follows(OH−) (iso)= +− (iso)EformationEF− E(OH ) − EOH− − E(perfect)(1)where E (iso) F− and E (iso) OH− are the energies for isolated fluorine andhydroxyl ions and E(OH − ) and E(perfect) are the totalenergies of the defective crystal containing a OH − impurity andthe perfect crystal, respectively. Our calculated OH − -impurityformation energy equals −1.00 eV, indicating that the totalenergy of a OH − -impurity system and an isolated F − is lowerthan the total energy of a perfect CaF 2 crystal and an isolatedOH − . It implicates that isolated hydroxyls are favorite to substitutefluorine ions in CaF 2 crystal. According to our previousdiscussion, the surface OH − impurities with Config HO (\) 11 havethe lowest energy, which means that the hydroxyl adsorptionon the CaF 2 surface is favorable energetically.On the other hand, the formation of OH − impurities in CaF 2crystal may also be due to the aggregation of separated oxygenand hydrogen impurities. To verify this aggregation, we calculatedthe association energy, defined as the energy differencebetween the remote oxygen and hydrogen impurities, and theOH − impurity. The corresponding value is +6.12 eV. With thisdefinition, the positive sign indicates stable aggregation. In thisformation mode, there should be isolated oxygen and hydrogenimpurities in CaF 2 crystal. Similar to the calculation on theformation energy of the OH − impurity in CaF 2 crystal, we alsocalculated the formation energies of the oxygen and hydrogen6398dx.doi.org/10.1021/jp211075g | J. Phys. Chem. C 2012, 116, 6392−6400
Page 1: Articlepubs.acs.org/JPCCAb Initio C
Page 4 and 5: The Journal of Physical Chemistry C
Page 8 and 9: The Journal of Physical Chemistry C

Ab Initio Calculations of Hydroxyl Impurities in CaF2

Create successful ePaper yourself

Delete template?

Save as template?