Vol. 10 No 5 - Pi Mu Epsilon

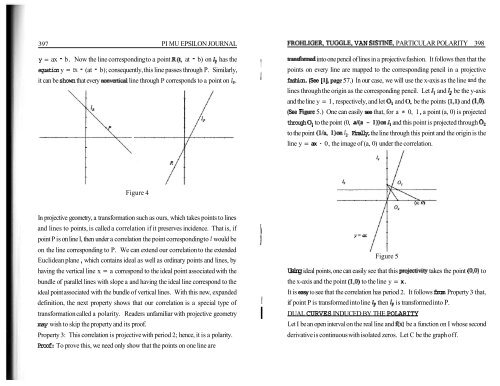
397 PI MU EPSILON JOURNALy = ax - b . Now the line corresponding to a point R(t, at - b) on lp has theequation y = tx - (at - b); consequently, this line passes through P. Similarly,it can be shown that every nonvertical line through P corresponds to a point on lp.FROHLIGER, TUGGLE, VAN SISTINE, PARTICULAR POLARITY 398donned into one pencil of lines in a projective fashion. It follows then that thepoints on every line are mapped to the corresponding pencil in a projectivefashion. (See [I], page 57.) In our case, we will use the x-axis as the line &d thelines through the origin as the corresponding pencil. Let li and li be the y-axisand the line y = 1, respectively, and let Ol and 0, be the points (1,l) and (1,O).(See Rgure 5.) One can easily see that, for a * 0, 1 , a point (a, 0) is projectedthrough Ol to the point (0, a/(a - 1))on li and this point is projected through 0,to the point (11% 1)on 1,. Finally, the line through this point and the origin is theline y = ax - 0, the image of (a, 0) under the correlation.Figure 4In projective geometry, a transformation such as ours, which takes points to linesand lines to points, is called a correlation if it preserves incidence. That is, ifpoint P is on line I, then under a correlation the point corresponding to i would beon the line corresponding to P. We can extend our correlation to the extendedEuclidean plane , which contains ideal as well as ordinary points and lines, byhaving the vertical line x = a correspond to the ideal point associated with thebundle of parallel lines with slope a and having the ideal line correspond to theideal point associated with the bundle of vertical lines. With this new, expandeddefinition, the next property shows that our correlation is a special type oftransformation called a polarity. Readers unfamiliar with projective geometrymay wish to skip the property and its proof.Property 3: This correlation is projective with period 2; hence, it is a polarity.Proof: To prove this, we need only show that the points on one line areFigure 5Using ideal points, one can easily see that this projectivity takes the point (0,O) tothe x-axis and the point (1,O) to the line y = x.It is easy to see that the correlation has period 2. It follows from Property 3 that,I if point P is transformed into line lp then lp is transformed into P.IDUAL CURVES INDUCED BY THE POLARITYLet I be an open interval on the real line and ex) be a function on I whose secondderivative is continuous with isolated zeros. Let C be the graph off.