Vol. 10 No 5 - Pi Mu Epsilon

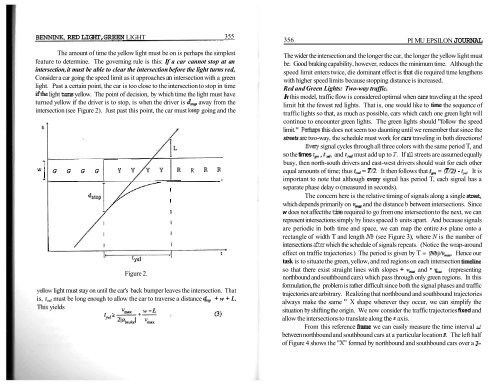
BENNINK, RED LIGHT, GREEN LIGHT 355The amount of time the yellow light must be on is perhaps the simplestfeature to determine. The governing rule is this: If a car cannot stop at anintersection, it must be able to clear the intersection before the light turns red,Consider a car going the speed limit as it approaches an intersection with a greenlight. Past a certain point, the car is too close to the intersection to stop in timeifthe light turns yellow. The point of decision, by which time the light must haveturned yellow if the driver is to stop, is when the driver is dsOp away from theintersection (see Figure 2). Just past this point, the car must keep going and the/ lLG G G G Y T / l R R R R^stopFigure 2.~-eIlovv light must stay on until the car's back bumper leaves the intersection. Thatis, td must be long enough to allow the car to traverse a distance dop + w + L.yieldsIII356 PI MU EPSILON JOURNALThe wider the intersection and the longer the car, the longer the yellow light mustbe. Good braking capability, however, reduces the minimum time. Although thespeed limit enters twice, die dominant effect is that die required time lengthenswith higher speed limits because stopping distance is increased.Red and Green Lights: Two-way traffic.In this model, traffic flow is considered optimal when cars traveling at the speedlimit hit the fewest red lights. That is, one would like to time the sequence oftraffic lights so that, as much as possible, cars which catch one green light willcontinue to encounter green lights. The green lights should "follow the speedlimit." Peihaps this does not seem too daunting until we remember that since thestreets are two-way, the schedule must work for cars traveling in both directions!Evay signal cycles through all three colors with the same period T, andso the times tà , tã., and fd must add up to T. If all streets are assumed equallybusy, then north-south drivers and east-west drivers should wait for each otherequal amounts of time; thus tras = 772. It then follows that t-, = (T.2) - tã, It isimportant to note that although eveq signal has period T, each signal has aseparate phase delay 0 (measured in seconds).The concern here is the relative timing of signals along a single street,which depends primarily on urn.-- and the distance b between intersections. Sincew does not affect the time required to go from one intersection to the next, we canrepresent intersections simply by lines spaced b units apart. And because signalsare periodic in both time and space, we can map the entire t-s plane onto arectangle of width T and length Nb (see Figure 3), where N is the number ofintersections after which the schedule of signals repeats. (Notice the wrap-aroundeffect on traffic trajectories.) The period is given by T = o/vrn=. Hence ourtask is to situate the green, yellow, and red regions on each intersection timelineso that there exist straight lines with slopes + vrnm and - (representingnorthbound and southbound cars) which pass through only green regions. In thisformulation, the problem is rather difficult since both the signal phases and traffictrajectories are arbitrary. Realizing that northbound and southbound trajectoriesalways make the same " X shape wherever they occur, we can simplify thesituation by shifting the origin. We now consider the traffic trajectories fixed andallow the intersections to translate along the s axis.From this reference frame we can easily measure the time interval &/between northbound and southbound cars at a particular location s. The left halfof Figure 4 shows the "X" formed by northbound and southbound cars over a 3-