An exact method for computing the area moments of ... - IEEE Xplore
An exact method for computing the area moments of ... - IEEE Xplore
An exact method for computing the area moments of ... - IEEE Xplore
- No tags were found...
Create successful ePaper yourself
Turn your PDF publications into a flip-book with our unique Google optimized e-Paper software.
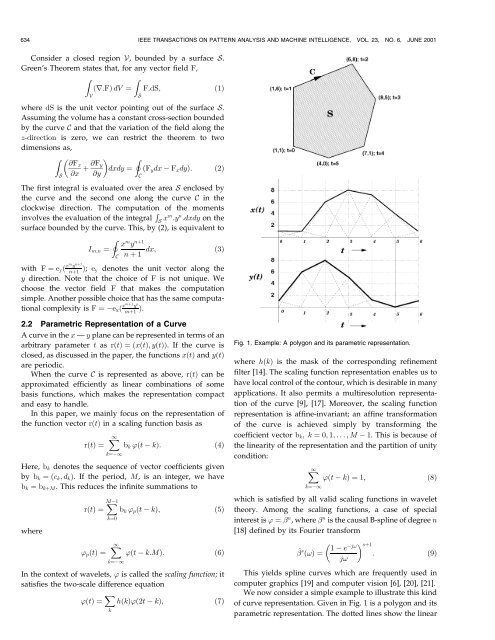
634 <strong>IEEE</strong> TRANSACTIONS ON PATTERN ANALYSIS AND MACHINE INTELLIGENCE, VOL. 23, NO. 6, JUNE 2001Consider a closed region V, bounded by a surface S.Green's Theorem states that, <strong>for</strong> any vector field F,ZZ…r:F† dV ˆ F:dS;…1†Vwhere dS is <strong>the</strong> unit vector pointing out <strong>of</strong> <strong>the</strong> surface S.Assuming <strong>the</strong> volume has a constant cross-section boundedby <strong>the</strong> curve C and that <strong>the</strong> variation <strong>of</strong> <strong>the</strong> field along <strong>the</strong>z-direction is zero, we can restrict <strong>the</strong> <strong>the</strong>orem to twodimensions as,Z @F xS @x ‡ @F Iydxdy ˆ …F y dx F x dy†: …2†@yCThe first integral is evaluated over <strong>the</strong> <strong>area</strong> S enclosed by<strong>the</strong> curve and <strong>the</strong> second one along <strong>the</strong> curve C in <strong>the</strong>clockwise direction. The computation <strong>of</strong> <strong>the</strong> <strong>moments</strong>involves <strong>the</strong> evaluation <strong>of</strong> <strong>the</strong> integral R S xm :y n :dxdy on <strong>the</strong>surface bounded by <strong>the</strong> curve. This, by (2), is equivalent toII m;n ˆCSx m y n‡1n ‡ 1 dx;with F ˆ e y … xm y n‡1n‡1 †; e y denotes <strong>the</strong> unit vector along <strong>the</strong>y direction. Note that <strong>the</strong> choice <strong>of</strong> F is not unique. Wechoose <strong>the</strong> vector field F that makes <strong>the</strong> computationsimple. <strong>An</strong>o<strong>the</strong>r possible choice that has <strong>the</strong> same computationalcomplexity is F ˆe x … xm‡1 y nm‡1 †.2.2 Parametric Representation <strong>of</strong> a CurveA curve in <strong>the</strong> x Ð y plane can be represented in terms <strong>of</strong> anarbitrary parameter t as r…t† ˆ…x…t†;y…t††. If <strong>the</strong> curve isclosed, as discussed in <strong>the</strong> paper, <strong>the</strong> functions x…t† and y…t†are periodic.When <strong>the</strong> curve C is represented as above, r…t† can beapproximated efficiently as linear combinations <strong>of</strong> somebasis functions, which makes <strong>the</strong> representation compactand easy to handle.In this paper, we mainly focus on <strong>the</strong> representation <strong>of</strong><strong>the</strong> function vector r…t† in a scaling function basis asr…t† ˆ X1kˆ1b k '…t k†:Here, b k denotes <strong>the</strong> sequence <strong>of</strong> vector coefficients givenby b k ˆ…c k ;d k †. If <strong>the</strong> period, M, is an integer, we haveb k ˆ b k‡M . This reduces <strong>the</strong> infinite summations towherer…t† ˆXM1kˆ0' p …t† ˆ X1kˆ1b k ' p …t k†;'…t k:M†:In <strong>the</strong> context <strong>of</strong> wavelets, ' is called <strong>the</strong> scaling function; itsatisfies <strong>the</strong> two-scale difference equation'…t† ˆXh…k†'…2t k†;…7†k…3†…4†…5†…6†Fig. 1. Example: A polygon and its parametric representation.where h…k† is <strong>the</strong> mask <strong>of</strong> <strong>the</strong> corresponding refinementfilter [14]. The scaling function representation enables us tohave local control <strong>of</strong> <strong>the</strong> contour, which is desirable in manyapplications. It also permits a multiresolution representation<strong>of</strong> <strong>the</strong> curve [9], [17]. Moreover, <strong>the</strong> scaling functionrepresentation is affine-invariant; an affine trans<strong>for</strong>mation<strong>of</strong> <strong>the</strong> curve is achieved simply by trans<strong>for</strong>ming <strong>the</strong>coefficient vector b k ;kˆ 0; 1; ...;M 1. This is because <strong>of</strong><strong>the</strong> linearity <strong>of</strong> <strong>the</strong> representation and <strong>the</strong> partition <strong>of</strong> unitycondition:X 1kˆ1'…t k† ˆ1;which is satisfied by all valid scaling functions in wavelet<strong>the</strong>ory. Among <strong>the</strong> scaling functions, a case <strong>of</strong> specialinterest is ' ˆ n , where n is <strong>the</strong> causal B-spline <strong>of</strong> degree n[18] defined by its Fourier trans<strong>for</strong>m^ s …!† ˆ 1 s‡1 ej!: …9†j!This yields spline curves which are frequently used incomputer graphics [19] and computer vision [6], [20], [21].We now consider a simple example to illustrate this kind<strong>of</strong> curve representation. Given in Fig. 1 is a polygon and itsparametric representation. The dotted lines show <strong>the</strong> linear…8†