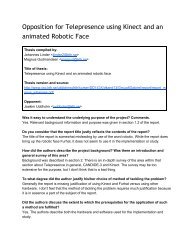
- Page 1: The spectrum of delay-differential
- Page 4 and 5: Acronyms DDE delay-differential equ
- Page 6 and 7: 3.3.2 Plotting critical curves . .
- Page 8 and 9: tion. The formula is not new. We cl
- Page 10 and 11: Matrix-Version der Lambert W-Funkti
- Page 12 and 13: Chapter 1 Introduction Many physica
- Page 14 and 15: An illustrative example The main co
- Page 16 and 17: Imag 50 0 −50 −4 −2 0 2 Real
- Page 18 and 19: Lambert W. This formula is valid fo
- Page 20 and 21: Chapter 2 Computing the spectrum 2.
- Page 22 and 23: 2.1. Introduction 11 For instance,
- Page 24 and 25: 2.1. Introduction 13 solved in each
- Page 26 and 27: 2.2. Methods for DDEs 15 of the typ
- Page 28 and 29: 2.2. Methods for DDEs 17 by definin
- Page 30 and 31: 2.2. Methods for DDEs 19 J = Wk(J)e
- Page 32 and 33: 2.2. Methods for DDEs 21 Proof: The
- Page 34 and 35: 2.2. Methods for DDEs 23 We note th
- Page 36 and 37: 2.2. Methods for DDEs 25 The soluti
- Page 40 and 41: 2.2. Methods for DDEs 29 −3τ 3τ
- Page 42 and 43: 2.2. Methods for DDEs 31 The idea o
- Page 44 and 45: 2.2. Methods for DDEs 33 where the
- Page 46 and 47: 2.2. Methods for DDEs 35 For instan
- Page 48 and 49: 2.2. Methods for DDEs 37 Chebyshev
- Page 50 and 51: 2.2. Methods for DDEs 39 (in time)
- Page 52 and 53: 2.2. Methods for DDEs 41 a delay-in
- Page 54 and 55: 2.2. Methods for DDEs 43 Example 2.
- Page 56 and 57: 2.2. Methods for DDEs 45 N = 3 N =
- Page 58 and 59: 2.3. Methods for nonlinear eigenval
- Page 60 and 61: 2.3. Methods for nonlinear eigenval
- Page 62 and 63: 2.3. Methods for nonlinear eigenval
- Page 64 and 65: 2.3. Methods for nonlinear eigenval
- Page 66 and 67: 2.3. Methods for nonlinear eigenval
- Page 68 and 69: 2.3. Methods for nonlinear eigenval
- Page 70 and 71: 2.3. Methods for nonlinear eigenval
- Page 72 and 73: 2.4. Numerical examples 61 π/(n +
- Page 74 and 75: 2.4. Numerical examples 63 We made
- Page 76 and 77: 2.4. Numerical examples 65 2.4.2 Ra
- Page 78: 2.4. Numerical examples 67 ance 10
- Page 81 and 82: 70 Chapter 3. Critical Delays where
- Page 83 and 84: 72 Chapter 3. Critical Delays 3.1 I
- Page 85 and 86: 74 Chapter 3. Critical Delays For r
- Page 87 and 88: 76 Chapter 3. Critical Delays the s
- Page 89 and 90:
78 Chapter 3. Critical Delays This
- Page 91 and 92:
80 Chapter 3. Critical Delays line
- Page 93 and 94:
82 Chapter 3. Critical Delays The m
- Page 95 and 96:
84 Chapter 3. Critical Delays after
- Page 97 and 98:
86 Chapter 3. Critical Delays for e
- Page 99 and 100:
88 Chapter 3. Critical Delays a Mö
- Page 101 and 102:
90 Chapter 3. Critical Delays form,
- Page 103 and 104:
92 Chapter 3. Critical Delays We no
- Page 105 and 106:
94 Chapter 3. Critical Delays two d
- Page 107 and 108:
96 Chapter 3. Critical Delays a par
- Page 109 and 110:
98 Chapter 3. Critical Delays The r
- Page 111 and 112:
100 Chapter 3. Critical Delays valu
- Page 113 and 114:
102 Chapter 3. Critical Delays h 2
- Page 115 and 116:
104 Chapter 3. Critical Delays The
- Page 117 and 118:
106 Chapter 3. Critical Delays Let
- Page 119 and 120:
108 Chapter 3. Critical Delays is w
- Page 121 and 122:
110 Chapter 3. Critical Delays Exam
- Page 123 and 124:
112 Chapter 3. Critical Delays case
- Page 125 and 126:
114 Chapter 3. Critical Delays asso
- Page 127 and 128:
116 Chapter 3. Critical Delays Lemm
- Page 129 and 130:
118 Chapter 3. Critical Delays Proo
- Page 131 and 132:
120 Chapter 3. Critical Delays and
- Page 133 and 134:
122 Chapter 3. Critical Delays and
- Page 135 and 136:
124 Chapter 3. Critical Delays Henc
- Page 137 and 138:
126 Chapter 3. Critical Delays wher
- Page 139 and 140:
128 Chapter 3. Critical Delays more
- Page 141 and 142:
130 Chapter 3. Critical Delays the
- Page 143 and 144:
132 Chapter 3. Critical Delays part
- Page 145 and 146:
134 Chapter 3. Critical Delays b)
- Page 147 and 148:
136 Chapter 3. Critical Delays whic
- Page 149 and 150:
138 Chapter 3. Critical Delays for
- Page 151 and 152:
140 Chapter 3. Critical Delays The
- Page 153 and 154:
142 Chapter 3. Critical Delays Clea
- Page 155 and 156:
144 Chapter 3. Critical Delays prob
- Page 157 and 158:
146 Chapter 4. Perturbation of nonl
- Page 159 and 160:
148 Chapter 4. Perturbation of nonl
- Page 161 and 162:
150 Chapter 4. Perturbation of nonl
- Page 163 and 164:
152 Chapter 4. Perturbation of nonl
- Page 165 and 166:
154 Chapter 4. Perturbation of nonl
- Page 167 and 168:
156 Chapter 4. Perturbation of nonl
- Page 169 and 170:
158 Chapter 4. Perturbation of nonl
- Page 171 and 172:
160 Chapter 4. Perturbation of nonl
- Page 173 and 174:
162 Chapter 4. Perturbation of nonl
- Page 175 and 176:
164 Chapter 4. Perturbation of nonl
- Page 177 and 178:
166 Chapter 4. Perturbation of nonl
- Page 179 and 180:
168 Chapter 4. Perturbation of nonl
- Page 181 and 182:
170 Chapter 4. Perturbation of nonl
- Page 183 and 184:
172 Appendix A. Appendix by ⎛ ⎜
- Page 185 and 186:
174 BIBLIOGRAPHY [Bau85] H. Baumgä
- Page 187 and 188:
176 BIBLIOGRAPHY [Bre06] , Solution
- Page 189 and 190:
178 BIBLIOGRAPHY [Dat78] R. Datko,
- Page 191 and 192:
180 BIBLIOGRAPHY [GMO + 06] M. Gu,
- Page 193 and 194:
182 BIBLIOGRAPHY [HS05] P. Hövel a
- Page 195 and 196:
184 BIBLIOGRAPHY [Lam91] J. Lambert
- Page 197 and 198:
186 BIBLIOGRAPHY [MGWN06] W. Michie
- Page 199 and 200:
188 BIBLIOGRAPHY [Nad69] S. B. Nadl
- Page 201 and 202:
190 BIBLIOGRAPHY [Pio07] M. Piotrow
- Page 203 and 204:
192 BIBLIOGRAPHY [SO06c] , A unique
- Page 205 and 206:
194 BIBLIOGRAPHY [Vos06a] , Iterati
- Page 207 and 208:
Index abstract Cauchy problem, 41,
- Page 209 and 210:
198 INDEX Nyquist criterion, 83 off
- Page 212 and 213:
Address: Institut Computational Mat