developing composite action in existing non-composite steel girder ...

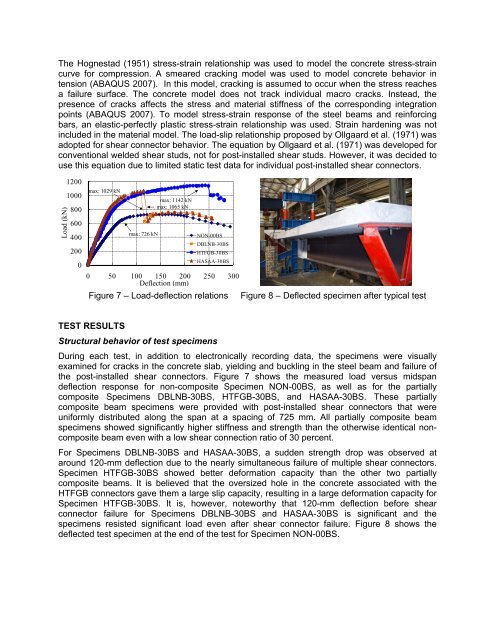
The Hognestad (1951) stress-strain relationship was used to model the concrete stress-straincurve for compression. A smeared cracking model was used to model concrete behavior intension (ABAQUS 2007). In this model, cracking is assumed to occur when the stress reachesa failure surface. The concrete model does not track individual macro cracks. Instead, thepresence of cracks affects the stress and material stiffness of the corresponding integrationpoints (ABAQUS 2007). To model stress-strain response of the steel beams and reinforcingbars, an elastic-perfectly plastic stress-strain relationship was used. Strain hardening was notincluded in the material model. The load-slip relationship proposed by Ollgaard et al. (1971) wasadopted for shear connector behavior. The equation by Ollgaard et al. (1971) was developed forconventional welded shear studs, not for post-installed shear studs. However, it was decided touse this equation due to limited static test data for individual post-installed shear connectors.Load (kN)120010008006004002000max: 1029 kNmax: 1142 kNmax: 1065 kNmax: 726 kNNON-00BSDBLNB-30BSHTFGB-30BSHASAA-30BS0 50 100 150 200 250 300Deflection (mm)Figure 7 – Load-deflection relations Figure 8 – Deflected specimen after typical testTEST RESULTSStructural behavior of test specimensDuring each test, in addition to electronically recording data, the specimens were visuallyexamined for cracks in the concrete slab, yielding and buckling in the steel beam and failure ofthe post-installed shear connectors. Figure 7 shows the measured load versus midspandeflection response for non-composite Specimen NON-00BS, as well as for the partiallycomposite Specimens DBLNB-30BS, HTFGB-30BS, and HASAA-30BS. These partiallycomposite beam specimens were provided with post-installed shear connectors that wereuniformly distributed along the span at a spacing of 725 mm. All partially composite beamspecimens showed significantly higher stiffness and strength than the otherwise identical noncompositebeam even with a low shear connection ratio of 30 percent.For Specimens DBLNB-30BS and HASAA-30BS, a sudden strength drop was observed ataround 120-mm deflection due to the nearly simultaneous failure of multiple shear connectors.Specimen HTFGB-30BS showed better deformation capacity than the other two partiallycomposite beams. It is believed that the oversized hole in the concrete associated with theHTFGB connectors gave them a large slip capacity, resulting in a large deformation capacity forSpecimen HTFGB-30BS. It is, however, noteworthy that 120-mm deflection before shearconnector failure for Specimens DBLNB-30BS and HASAA-30BS is significant and thespecimens resisted significant load even after shear connector failure. Figure 8 shows thedeflected test specimen at the end of the test for Specimen NON-00BS.