Hubbard Model for Asymmetric Ultracold Fermionic ... - KOMET 337

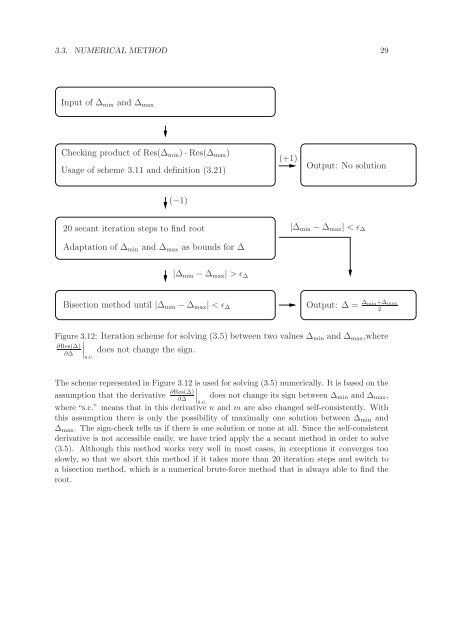
3.3. NUMERICAL METHOD 29Input of ∆ min and ∆ maxChecking product of Res(∆ min ) · Res(∆ max )Usage of scheme 3.11 and definition (3.21)(+1)Output: No solution(−1)20 secant iteration steps to find root|∆ min − ∆ max | < ǫ ∆Adaptation of ∆ min and ∆ max as bounds for ∆|∆ min − ∆ max | > ǫ ∆Bisection method until |∆ min − ∆ max | < ǫ ∆Output: ∆ = ∆ min+∆ max2Figure 3.12: Iteration scheme for solving (3.5) between two values ∆ min and ∆ max ,where∣ does not change the sign.s.c.∂Res(∆)∂∆The scheme represented in Figure 3.12 is used for solving (3.5) numerically. It is based on theassumption that the derivative ∂Res(∆)∂∆ ∣ does not change its sign between ∆ min and ∆ max ,s.c.where “s.c.” means that in this derivative n and m are also changed self-consistently. Withthis assumption there is only the possibility of maximally one solution between ∆ min and∆ max . The sign-check tells us if there is one solution or none at all. Since the self-consistentderivative is not accessible easily, we have tried apply the a secant method in order to solve(3.5). Although this method works very well in most cases, in exceptions it converges tooslowly, so that we abort this method if it takes more than 20 iteration steps and switch toa bisection method, which is a numerical brute-force method that is always able to find theroot.