Hubbard Model for Asymmetric Ultracold Fermionic ... - KOMET 337

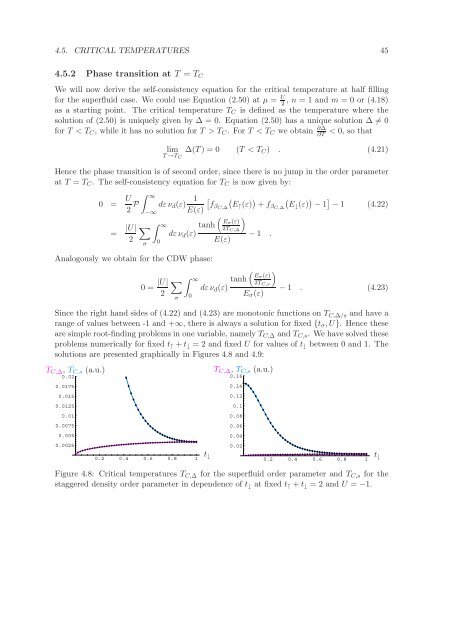
4.5. CRITICAL TEMPERATURES 454.5.2 Phase transition at T = T CWe will now derive the self-consistency equation for the critical temperature at half fillingfor the superfluid case. We could use Equation (2.50) at µ = U 2, n = 1 and m = 0 or (4.18)as a starting point. The critical temperature T C is defined as the temperature where thesolution of (2.50) is uniquely given by ∆ = 0. Equation (2.50) has a unique solution ∆ ≠ 0for T < T C , while it has no solution for T > T C . For T < T C we obtain ∂∆∂T< 0, so thatlim ∆(T) = 0 (T < T C ) . (4.21)T →T CHence the phase transition is of second order, since there is no jump in the order parameterat T = T C . The self-consistency equation for T C is now given by:0 = U ∫ ∞2 P 1 [ (dεν d (ε) fβC,∆ E↑ (ε) ) (+ f βC,∆ E↓ (ε) ) − 1 ] − 1 (4.22)−∞ E(ε)( )= |U| ∑∫ ∞ tanh Eσ(ε)2T C,∆dεν d (ε)− 1 .2E(ε)Analogously we obtain for the CDW phase:σ00 = |U|2∑σ∫ ∞0dεν d (ε)( )tanh Eσ(ε)2T C,sE σ (ε)− 1 . (4.23)Since the right hand sides of (4.22) and (4.23) are monotonic functions on T C,∆/s and have arange of values between -1 and +∞, there is always a solution for fixed {t σ ,U}. Hence theseare simple root-finding problems in one variable, namely T C,∆ and T C,s . We have solved theseproblems numerically for fixed t ↑ + t ↓ = 2 and fixed U for values of t ↓ between 0 and 1. Thesolutions are presented graphically in Figures 4.8 and 4.9:T C,∆ , T C,s (a.u.)0.020.01750.0150.01250.010.00750.0050.00250.2 0.4 0.6 0.8 1t ↓T C,∆ , T C,s (a.u.)0.160.140.120.10.080.060.040.020.2 0.4 0.6 0.8 1Figure 4.8: Critical temperatures T C,∆ for the superfluid order parameter and T C,s for thestaggered density order parameter in dependence of t ↓ at fixed t ↑ + t ↓ = 2 and U = −1.t ↓