High Availability Theoretical Basics - Schneider Electric

Mathematics Basics
High Availability Theoretical Basics
In many situations a detected disruption fortunately does not mean the end of a
device’s life. This is usually the case for the automation and control systems being
discussed, which are repairable entities. As a result, the ability to predict the number
of shutdowns, due to a detected disruption over a specified period of time, is useful to
estimate the budget required for the replacement of inoperative parts.
In addition, knowing this figure can help you maintain an adequate inventory of spare
parts. Put simply, the question "Will a device work for a particular period" can only be
answered as a probability; hence the concept of Reliability.
According to the MIL-STD-721C standard, the definition of reliability R(t) of a given
system is the probability of that system to perform its intended function under stated
conditions for a stated period of time. As an example, a system featured by 0.9999
reliability over a year has a 99.99% probability of functioning properly throughout an
entire year.
Note: The reliability is systematically indicated for a given period of time, for example
one year.
Referring to the system model we considered with the "bathtub curve,” one
characteristic is its constant Failure Rate, during the useful life. In that portion of its
lifetime, the Reliability of the considered system will follow an exponential law, given
by the following formula: R(t) = e -λt , where λ stands for the Failure Rate.
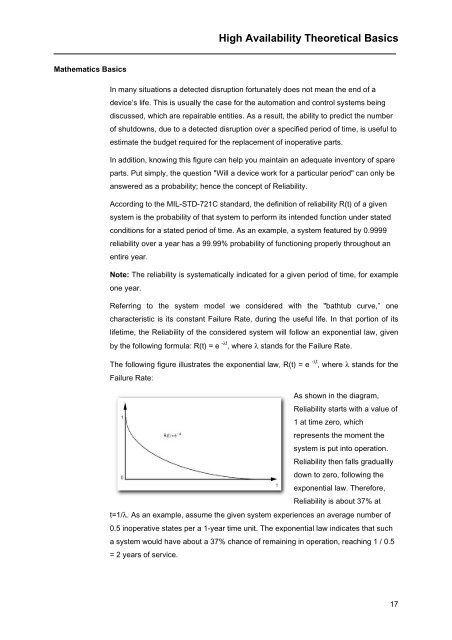
The following figure illustrates the exponential law, R(t) = e -λt , where λ stands for the
Failure Rate:
As shown in the diagram,
Reliability starts with a value of
1 at time zero, which
represents the moment the
system is put into operation.
Reliability then falls graduallly
down to zero, following the
exponential law. Therefore,
Reliability is about 37% at
t=1/λ. As an example, assume the given system experiences an average number of
0.5 inoperative states per a 1-year time unit. The exponential law indicates that such
a system would have about a 37% chance of remaining in operation, reaching 1 / 0.5
= 2 years of service.
17