libro de trigonometria preuniversitaria nivel uni click aqui para ver

Capítulo
1
RAZONES TRIGONOMÉTRICAS
DEUN ÁNGULOAGUDO- I
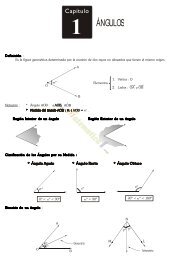
DEFINICIÓN: Son los resultados que se obtienen al dividir los lados de un triángulo rectángulo.
En el triángulo adjunto, tenemos:
b
C
A c B
a
a y c : catetos
b : hipotenusa
B : recto
A y C : s agudos
2
a
2
c
2
b
A + C = 90º
A los resultados así obtenidos se les asigna un nombre asociado a uno de los ángulos agudos del triángulo. Así en el gráfico;
para  tenemos:
a : cateto opuesto (CO) b : hipotenusa (H) c : cateto adyacente (CA)
Luego se definen :
Por ejemplo:
13
SenA
CosA
TanA
12
CO
H
CA
H
a
b
c
b
CO a
CA c
5
Sen
Cos
* TRIÁNGULOS RECTÁNGULOS DE ÁNGULOS NOTABLES: Son aquellos triángulos rectángulos en los cuales
conociendo las medidas de sus ángulos agudos se pude establecer la proporción en la que se encuentran los lados de
dicho triángulo. Dos de los más usados son :
2
45º
1
CscA
SecA
CotA
45º
30º
1
3
Mientras que uno aproximado, pero reconocido por sus diversas aplicaciones es el de 37º y 53º.
37º
5
4
5
13
12
13
H
CO
H
CA
CA
CO
2
53º
;
;
3
b
a
b
c
c
a
Tan
Cot
60º
5
12
12
5
1

A partir de estos se determinarán otros adicionales como:
No olvide además:
* PROPIEDADES:
4 + 2 2
22º30'
2 +1
5
26º30'
2
Sen
Cos
Tan
67º30'
63º30'
1
1
8º
15º
5 2
4
7
6 + 2
82º
75º
1
6 - 2
16º
10
18º30'
25
30º 37º 45º 53º 60º
1
2
3
2
3
3
Cot 3
Sec
2 3
3
Csc 2
3
5
4
5
3
4
4
3
5
4
5
3
2
2
2
2
1
1
2
2
4
5
3
5
4
3
3
4
5
3
5
4
3
2
1
2
3
3
3
2
2 3
3
24
3
74º
71º30'
I. Las razones trigonométricas de un ángulo; dependerán de la medida de dicho ángulo y no de los lados del
triángulo rectángulo en que se ubique. Por ejemplo:
C
A
Q
M
N
P B
Sen
Sen
Sen
PQ
AQ
MN
Iguales
AN
BC
AC
II. R. T. Recíprocas: Se nota claramente, de las definiciones de las razones trigonométricas de un ángulo agudo, que
existen tres parejas que son una la recíproca inversa de la otra, por lo que su producto es siempre igual a 1. Estas
parejas son las siguientes:
Sen
Csc
Note que los ángulos agudos, deben ser iguales. Por ejemplo si nos dicen que :
Tan(3x - 10º) . Cot(x + 30º) = 1; para calcular "x" diremos :
Tan(3x - 10º) . Cot(x + 30º) = 1 3x - 10º = x + 30º x = 20º
1
Cos
Sec
III. R. T. de Ángulos Complementarios: Cuando se calculan las razones trigonométricas de los 2 ángulos agudos
de un triángulo rectángulo, se puede notar que existen ciertas parejas de éstas que toman el mismo valor. Esta
característica la vamos a indicar de la siguiente manera:
1
Tan
Cot
1
7
1

Si: son agudos; tales
que: + = 90º
entonces:
Sen = Cos
Tan = Cot
Sec = Csc
Por ejemplo:
Sen10º = Cos80º
Tan20º = Cot70º
Sec40º = Cos 50º
Cos24º = Sen 66º
Tan = Cot (90º )
Sen( + 10º) = Cos (8 0º )
o
Si:
que:
son agudos; tales
Sen = Cos
Tan = Cot
Sec = Csc
entonces: = 90º
Por ejemplo: hallar "x", si:
Sen (2x + 10º) = Cos3x
2x + 10º + 3x = 90º
5x = 80º x = 16º
Otro ejemplo; hallar "x" si:
Tan (2x + y) = Cot (x - y)
2x + y + x y = 90º
3x = 90º x = 30º

01. Si " " es la medida de un ángulo agudo y se cumple
que:
Tg
2
; calcular: T 13Sen
12Cot
3
a) 12 b) 14 c) 16
d) 18 e) 20
02. En un triángulo rectángulo ABC recto en "C" se cumple
que: 4SenA=7SenB; calcular: 2
E 65Sen
A 42TgB
a) 10 b) 15 c) 20
d) 25 e) 30
03. El perímetro de un triángulo rectángulo es 150u y la
cosecante de uno de los ángulos agudos es 2,6.
Calcular la longitud del mayor cateto.
a) 20 u b) 30 u c) 40 u
d) 50 u e) 60 u
04. Del gráfico mostrado, calcular: " Cot . Cot
B
"
A
2a
a) 2 b) 4 c) 6
d) 8 e) 3/2
05. Del gráfico mostrado, calcular: " Tg
es un cuadrado.
Tgw"
, si: ABCD
B
w
C
2a
A
a) 0,1 b) 0,2 c) 0,3
d) 0,4 e) 0,5
E
a
E
3a
06. Del gráfico, calcular: " Cot " , si: Cot 2,
4
B C
A
a) 1 b) 2 c) 3
d) 4 e) 5
E
D
EJERCICIOS PROPUESTOS
F
D
C
07. Del gráfico, calcular: " Tg " , si:
a) 0,5 b) 1 c) 1,5
d) 2 e) 2,5
08. Calcular:
E
4Tg
4
w
6Sen
6
a) 5,5 b) 6,5 c) 7,5
d) 8,5 e) 9,5
09. Calcular:
E
Tgw
3Cos
2
Cot 30º.
Sec60º.
Cot45º
2Tg
2
30º
Sec
2
45º
a) 2 b) 2,25 c) 2,5
d) 2,75 e) 3
10. Del gráfico, calcular: Cot
A
O
37º
a) 1 b) 2 c) 3
d) 4 e) 5
11. Si ABC es un triángulo equilátero, calcular: " Tg "
3
a)
5
d)
2 3
7
A
b)
e)
M
2 3
5
3 3
7
F
B
E
2
N
B
3
c)
7
8
3
5
12
C

12. Del gráfico mostrado, calcular: 11Tan
B C
A
37º
a) 1 b) 2 c) 3
d) 4 e) 5
13. Del gráfico mostrado, calcular: " Cotw"
.
w
a) 1 b) 1,5 c) 2
d) 2,5 e) 3
a
E
F
4a
45º
45º
14. Del gráfico mostrado, calcular:
cuadrado.
" Tg " , si: ABCD es un
B C
37º
E
A
D
F
a) 3/4 b) 3/7 c) 4/7
d) 3/5 e) 3/8
15. Si se cumple que: Sen2x = Cos3x para "x" agudo,
calcular: E = 4Tg(2x+1º)+3Tg(3x-1º).
a) 5 b) 6 c) 7
d) 8 e) 9
16. Si se cumple que: Sen(3x-17º)Csc(x+13º) = 1
Calcular: E = Csc2x+Cot3x+Sec4x
a) 5 b) 6 c) 7
d) 8 e) 9
17. Calcular: E = (3Tg10º+8Cot80º)Cot10º
a) 10 b) 11 c) 12
d) 13 e) 14
18. Calcular: E = (5Sen20º+3Cos70º)(5Csc20º-2Sec70º)
a) 20 b) 22 c) 24
d) 26 e) 28
19. Sabiendo que: Tg(3x-10º)Tg40º = 1
Calcular: E = 3Sec3x+5Sen(2x-3º)
D
a) 5 b) 6 c) 7
d) 8 e) 9
20. Si: SenxSecy = 1, con x e y agudos.
x y x y
Calcular: E Tg(
). Cot(
). Tgx.
Tgy
2 3
a) 1 b) 2 c) 3
d) 5 e) 6
21. En un triángulo rectángulo, los lados menores miden
3 cm y 5 cm. Si el menor ángulo agudo de dicho
triángulo mide " ".
Halle el valor de: W
2
17Sen
1
a) 1,5 b) 2,5 c) 3,5
d) 4,5 e) 5,5
22. En un triángulo ABC, recto en C, se sabe :
Calcular :
E
13
SecA
SecB
CosA
a) 1 b) 2 c) 3
d) 4 e) 5
2
3
3
CtgB
23. En un triángulo rectángulo, el Coseno de uno de sus
ángulos agudos es 0,96.
Si su hipotenusa mide 50 m.
Hallar el perímetro de dicho triángulo.
a) 112 m b) 224 m c) 96 m
d) 52 m e) 412 m
24. Calcule el área de la región triangular ABC .
Donde: AC = 36m; si, además
CscA
17
CscC
a) 72 m 2 b) 144 m 2 c) 108 m 2
d) 18 m 2 e) 360 m 2
25. El perímetro de un triángulo rectángulo es de 338 m.
Si la tangente de uno de los ángulos agudos es 2,4.
¿Cuánto mide el cateto menor?
a) 13 m b) 33,8 m c) 50 m
d) 56,33 m e) 55 m
26

26. De la figura, hallar
( Tan
2 mn
2
2)
n
a) 1 b) 4 c) 2
d) 3 e) 0
27. Determinar la hipotenusa de un triángulo rectángulo,
sabiendo que la suma de sus catetos es 6 m y el
producto de los Senos de los ángulos agudos es 0,22.
a) 3 m b) 4 m c) 5 m
d) 6 m e) 7 m
28. Del gráfico, calcule : Tan .
Si: BN = 2AN
m
C
45º
A N B
a) 0,25 b) 0,5 c) 0,6
d) 0,8 e) 0,75
29. Si en el gráfico : AB = BC.
Calcule: Tan
B
2
a)
9
1
d)
3
A
4
b)
9
2
e)
5
30. Del gráfico, obtener Tan
A
O
37º
M
2
c)
3
M
53º
C
B
M
4
a)
3
31. Si:
2
d)
3
Calcular:
f
( x)
f
( 2)
a) 0
2 b)
3
b)
4
4
e)
5
Csc
3n
d) 3
2 e) 0
5
c)
4
Tan
2n
1
2 c) 2
2
2 Cos
n
32. Si en el triángulo ABC, equilátero, M, N y P son puntos
medios de AB, BC y AC, respectivamente.
Además: NQ = 2QP
Calcular:
K
7Tan
5Tan
Tan
B
M N
Q
A P
C
a) 3
b) 4 c) 6
d) 8 e) 14
Sen
3
33. Si: x y ( Tanx)
2 1
2
El valor de "q" es: q
2
a) 2 b)
3
1
d)
2
1
e)
3
34. Del gráfico, calcular: Cot
Si: ABCD: cuadrado.
B C
A
37º
1
1
D
2
Tan x
2
Ctg x
c) 3
a) 6 b) 12 c) 9
d) 18 e) 14
1

35. Si:
Sen 3x . Cscy = 1
Tan(2x + 20º) = Ctg(y + 10º)
Determinar "y - x"
a) 12º b) 18º c) 20º
d) 24º e) 32º
36. Si: Tgx . Tgy = 1
Determinar:
6
a)
3
5
d)
3
E
Sen
x y
2
6
b)
6
2
e)
6
Tan
x y
3
c) 1
Sec2
x y
3
37. Calcular:
E = 4Sen20º (Csc20º + 2Sec70º)
a) 12 b) 10 c) 8
d) 6 e) 16
38. Calcule el valor de la expresión:
W
Sec10º
Sec20º
Sec30º
... Sec80
º
Csc10º
Csc20º
Csc30º
... Csc80º
a) 1 b) 2 c) 2
d) 3 e) 3 2
39. Hallar los ángulos agudos y tales que:
Tan(
3
2
35º
)
15º
a) 11º y 10º b) 15º y 13º
c) 20º y 17º30' d) 35º y 25º
e) 17º y 16º
Ctg(
90º
40. Siendo:
Sen(2x+y) . Sen(x-y+10º) = Cos (x+2y) . Cos (80º -
x + y)
Calcule:
K = Cot(x+y) . Cot(5x-2y) . Cot(5y-2x)
a) 1 b) 2 c) 3
3
d) 3 e)
3
41. Se tiene dos circunferencias tangentes exteriormente
con radios R y r.
Calcular el cuadrado de la cotangente del ángulo
formado por la recta tangente a ambas circunferencias
y la recta que une los centros.
)
4Rr
a) 2
( R r)
2Rr
c) 2
( R r)
Rr
e)
( R r)
2
4Rr
b) 2
( R r)
2Rr
d) 2
( R r)
42. Se tiene un triángulo rectángulo con catetos a y b.
Hallar su área en términos de "m" si:
b
a
2
t
t
2
t
2
2mt
a) m
2
1 b)
c)
m
2
1
2
e) m 1
2
2
tSec
3
tCsc
6
d)
Tan
4
2Sen
6
2Cos
m
2
1
2
3
2
m
2
( m
2
1)
2
2
43. En la figura, calcular el valor de x, si se cumple la
siguiente condición:
x
Tan(
30º
)
Ctg(
30º
20m
3 )
a) 10 2 m b) 10 m c) 5 3 m
d) 5 m e) 10 3 m
44. Una semicircunferencia de radio ( 1 3)
cm. se divide
en treinta arcos iguales.
Calcular la proyección del arco comprendido entre la
quinta y décima división sobre el diámetro horizontal
en centímetros.
1
a)
4
5
d)
4
1
b)
2
e) 2
c) 1
45. Si para un observador en la Tierra, el Sol aparece bajo
un ángulo de 32' y si la distancia del observador a la
superficie de Sol es 150 millones de kilómetros.
Determinar el radio del Sol en millones de kilómetros
sabiendo que:
Sen16' = 0,00465
0

a) 0,70 b) 0,819 c) 1,395
d) 2,629 e) 1,402
46. En un triángulo isósceles, las medianas trazadas de sus
vértices de ángulos iguales se intersecan
perpendicularmente.
Entonces, el Coseno de uno de los ángulos iguales es:
1
a)
3
1
d)
10
1
b)
2
1
e)
2 3
3
c)
2
47. Dos autos parten simultáneamente desde un punto "P"
en direcciones que forman un ángulo " " uno a
5 km/h y el otro a 12 km/h.
Calcular el Cos sabiendo que al cabo de 1 hora la
distancia desde el punto "P" al punto medio del
segmento que separa ambos autos es de 7 km.
5
a)
8
9
d)
40
7
b)
16
13
e)
25
3
c)
80
48. En el trapecio ABCD : BC // AD.
Si: AB = BC = 8; CD = 15 y AD = 25 y la medida del
ángulo DA D ˆ
Si: AB = BC = 8; CD = 15 y AD = 25 y la medida del
C ; el valor de:
K = CscD + CtgD ; es:
a) 1 b) 2 c) 3
d) 4 e) 5
49. En un triángulo rectángulo ABC B 90º
) ˆ
equivalente de:
( señale el
K
a) Sen A
2
d) Cot A
2
TanA
Tan
A
2
1
TanA
b) Cos A
2 c) Tan A
2
e) Sec A
2
50. Si: 3 es un ángulo agudo, tal que:
Cot3
Calcule: K 5Csc
6Cos2
a) 1 b) 2 c) 3
d) 4 e) 5
2
5
Cot
A
2
51. Si los triángulos ABC, CDE y EFG son equiláteros.
Tanx
Calcule:
Tany
Si: AC
CE
3
EG
2
1
35
a)
66
13
d)
11
A
B
C
M
65
b)
77
5
e)
7
D
x y
N
55
c)
72
52. Del gráfico, hallar: Tan
B m E n F p C
a)
d)
n
n
m
m
p
m
n
p
A
b)
e)
n
n
p
p
m
p
n
n
53. Si:
Tan(x+10º)+Tan(y+10º)=Cot(x+10º)+Cot(y+10º)
Calcular:
c)
m
m
Cos(
x y)
Cos(
4y
Sen(
100º
4y)
K
E
p
n
10º
)
F
Sec
2
( x 10º
) Sec
2
3y
Cos(
x y 10º
)
a) 4 b) 8 c) 16
d) 24 e) 32
54. Del gráfico, calcular:
K
2
3Cot
5Tan
Si: CD se dibuja con centro en "E"
B Q
C
P
60º
A E
D
a) 3 b) 5 c) 7
d) 8 e) 10
D
2
G

55. En el cuadrado ABCD; calcular:
K
3Tan
E
9Tan
B C
8º
A D
a) 3 b) 4 c) 5
d) 6 e) 7
56. Sabiendo que:
Tan(40º+x) . Sen(50º-x) = Cos(10º+x) ..... (1)
Tan(2x-5º) . Tany = Tan1º . Tan2º . Tan3º ...... Tan 89º
Calcule:
W
( y
2
Sec ( 2x
x 5º
)
5º
)
2
Tan ( y
a) 3 b) 5 c) 7
d) 9 e) 11
57. En el cuadrado ABCD, calcular:
5º
)
W 2 2Cos
5Cos
Si: AE = AF; CM = CN y CF = 3FD
M
B E C
A
N
a) 11 b) 13 c) 4 6
d) 19 e) 17
2
Csc
D
F
58. Sabiendo que:
Calcule:
Sen(
2x
Tan
W
x
2
y
3y
20º
)
2
Csc ( x
Tan
y)
a) 4 b) 6 c) 8
d) 10 e) 5
59. Del gráfico calcular:
W
( Csc
1)(
Csc
Cos
x
4
1)(
Csc
3x
2
3y
2
Csc 3y
2y
1
1)(
Csc
O1 O2 O3
a) 4 b) 9 c) 16
d) 81 e) 100
60. Del gráfico calcule:
W ( Sec 1)(
Sec 1)
Siendo "A" centro del arco BD.
B
Cos
Cos
A D T C
a) 1 b) 0 c) 2
d) 3
3
e)
2
O
1)

Claves
Claves
01.
02.
03.
04.
05.
06.
07.
08.
09.
10.
11.
12.
13.
14.
15.
16.
17.
18.
19.
20.
21.
22.
23.
24.
25.
26.
27.
28.
29.
30.
e
d
e
c
b
e
c
d
b
b
d
c
b
c
c
a
b
c
e
c
c
e
a
a
d
d
c
e
b
e
31.
32.
33.
34.
35.
36.
37.
38.
39.
40.
41.
42.
43.
44.
45.
46.
47.
48.
49.
50.
51.
52.
53.
54.
55.
56.
57.
58.
59.
60.
c
d
e
b
d
a
a
a
e
d
a
d
b
c
a
d
d
d
e
c
b
a
c
e
d
d
e
c
c
c

Capítulo
2
RAZONES TRIGONOMÉTRICAS
DE UN ÁNGULO AGUDO - II
* CÁLCULO DE LADOS: Es el procedimiento mediante el cual se determinan los lados faltantes de un triángulo
rectángulo, en términos de un lado que sí se conoce; y de un ángulo agudo que también se conoce.
Criterio:
Casos:
1 .
2 .
3 .
C
A L B
C
L
A B
L
C
A B
I)
II)
I)
II)
Lado desconocid o
Lado conocido
I)
II)
BC
L
AC
L
AB
L
AC
L
BC
L
AB
L
Tan
Cot
Sen
AB
R.
T.(
BC
AC
AC
BC
conocido)

* SUPERFICIE DE UN TRIÁNGULO: La superficie de un triángulo se puede calcular como el semiproducto de las
medidas de dos de sus lados, multiplicados por el Seno del ángulo que forman dichos lados.
S ABC
ab
SenC
2
Análogamente
S ABC
ac
2
SenB
A
S ABC
c
bc
2
h
B
b
SenA
a
C
Sabemos:
S ABC
S ABC
pero: h = aSenC
luego:
b
b h
2
aSenC
2

01. Hallar el área del triángulo, de la figura mostrada:
a) K Sen . Cos
2
K
b) ( K / 2)
Sen
2
EJERCICIOS PROPUESTOS
. Cos
c) ( K / 3)
Sen . Cos
2 d) ( K / 4)
Sen . Cos
2
e) ( K / 5)
Sen . Cos
2
02. En un triángulo isósceles ABC (AB=BC) se sabe que
los ángulos congruentes miden " " mientras que el
lado desigual mide "L". Hallar uno de los lados
congruentes.
L
a) Sec
2
d)
L
2
Ctg
b)
03. Obtener "x", en:
L
2
Csc
L
e) Cos
2
L
c) Tg
2
m
a) mSen b) mCos c) mSec
d) mCsc e) mTg
04. Obtener "x"
O
R
H x
a) R( 1 Sen ) b) R(
Sec 1)
c) R( 1 Cos ) d) R(
Csc 1)
e) R(
1 Tg )
A
B
05. En la figura, halla "x".
A
m
B
a) mSen nCos b) mCos nCos
c) mCos nSen d) mSec nSec
e) mSen nSec
06. Halla "x" en:
x
A C
x
B
m
a) mSec Tg b) mCos Csc
c) mCos Ctg d) mSen Cos
e) mTg
07.
Halla "x":
m
a) mSen . Cot b) mSen . Tan
c) mSen . Sen d) mCos . Cot
e) mCos . Tan
08. Hallar "x":
a)
A
B
m
2
mSen b)
x
2
mCos
n
C
c) mSen Cos d) mSen Tg
e)
mSec
Csc
C
D
D
x
H

09. Hallar "x", de la figura:
x
m
a) mSen . Cos b) Sen . Cos
c) mSen
e) mTg
10. Del gráfico, hallar: AC .
C
m
d) mCos
B
n
x y
a) mSenx+nSeny b) mCosx+nSeny
c) nSenx+mCosy
e) mSeny+nCosx
d) mCosx+nCosy
11. Del gráfico, hallar "x", si: ABCD es cuadrado.
A B
D
m
a) m( 1 Sen ) b) m(
1 Cos )
c) m( 1 Tg ) d) m(
1 Ctg )
e) m(
Tg Ctg )
12. Obtener "AB":
A
O
a) R( Csc Ctg ) b) R(
1 Ctg )
c) R( 1 Csc ) d) R(
1 Sen )
e) 2R+1
R
C
x
A
C
B
13. Hallar "x", siendo "O" centro del sector AOB.
a) RSen
x
A
O
R
B
b) RCos
c) R( 1 Sen )
d) R(
1 Cos )
e) R(
1 2Cos
)
14. Hallar "x".
a) mSen Sen
b) mSen Cos
c) mCos Cos
d) mCos Sen
e) mTg Ctg
m
15. Hallar la distancia mínima del punto "P" a la
circunferencia:
P
2
a) RCsc b) R(
Csc 1)
c) R( Tg 1)
d) R(
Ctg 1)
e) R(
Csc 1)
16. Determine "x" en:
A
a) mSen . Cos
b) mSen . Sec
c) mSen . Ctg
d) mCos . Ctg
e) mCos . Tg
x
x
D
R
m
C
B

17. Hallar "x".
B
a
A
x
a) Sen aCos b) bSen Cos
c) bSen aCos d) aSen bCos
e) aSec bTg
18. Determine el perímetro del triángulo ABC.
A
a) m(
1 Sen Cos )
b) m(
1 Sec Tg )
c) m(
1 Csc Ctg )
d) m(
1 Sec Csc )
e) m(
1 Tg Ctg )
19. Hallar: "x" en:
m
a) mCtg Cos b) mTg . Cos
b
C
c) mTg Sen d) mTg
e) mSen
20. Del gráfico, hallar: "Ctgx".
a)
c)
e)
x
2Sec
Cos
Sen
Sec Cos
Sen
Sec Cos
Sen
b)
d)
B
D
x
m
Sen Cos
Sen
Csc Sen
Cos
C
21. Del gráfico, determine "x".
m
a) m Sen b) m Cos c) m Sec
d) m Csc e) m Tan
22. Determinar CD .
B
m
C D
a) mTan Sen b) mCtg Cos
c) mTan Cos d) mTan Csc
e) mCtg Sen
23.
Del gráfico, hallar "x".
a)
c)
m
Tan
1
m
Ctg
1
e) m(
1 Tan )
m
24. Determine "x" en :
b)
d)
m
Ctg
1
m
Tan
1
x
x
A
m x
a) m Sen Sen b) m Sen Cos
c) m Sen Sec d) m Cos Sec
e) m Cos Sen
45°

25. Determine "x" en:
a) 2
m Sec b) 2
m Cos
c) 2
m Sen d) 2
m Csc
e) m Sec Csc
26. Si ABCD es un cuadrado, determine "x".
a)
A
L
2
L Sen b)
B
D
L
x
2
Cos
m
C x
c) L ( Sen Cos )
2
d) L Sen Cos
e) L Sen
2
Cos
27. Del gráfico, hallar "x":
m
a) m ( Sec
2
1)
b) m ( Csc
2
1)
c) 2
m ( Tan 1)
d)
2
m ( Ctg 1)
e) 2
m ( Tan
2
Ctg )
28. Del gráfico, hallar "x", si ABCD es un cuadrado.
A B
D
n
a) nSen b) nCos c) nTan Csc
d) nCsc e) nCtg
x
C
x
29. Del gráfico, hallar: ED.
E
m
A D B
a) mCtg b) mSec c) mSec2
d) mCtg 2 e) mTan2
30. En el gráfico, hallar MP, en términos de " " y " "; " "
y " ".
M
b
R
a) ( a b Cos ) Sec b) ( a b Cos ) Csc
c) ( a b Tan ) Ctg d) ( a bSec ) Tan
e) ( a bSen ) Csc
31. En un triángulo BAC, recto en A; la mediana BM y el
cateto AC forman un ángulo agudo x. Luego Tanx es
igual a:
N
a) 2TanC b) TanB + TanC
c) 2TanB d) TanC + CtgC
e) 2(TanC + TanB)
32. En la figura el área del triángulo ACD es igual al área
del triángulo ABC.
El valor de será:
D
a)
c)
ArcTan
1
b)
2
ArcTan
1
d)
2
e) ArcTan 2
a
A B
ArcCtg
ArcCtg
1
2
C
1
2
C
P

33. En la región limitada por una circunferencia de radio R
y dos tangentes a ésta; se quiere inscribir otra
circunferencia (de radio menor que R). Si las tangentes
se intersectan en un ángulo de 2a radianes, ¿A qué
distancia de la intersección de éstas, debe encontrarse
el centro de la circunferencia inscrita?
a)
R 1 Sena b)
Sena 1 Sena
c)
Sena
1 Sena
R
e) R
1 Sena
Sena
R
Sena
d)
R
1 Sena
Sena
1
1
Sena
Sena
34. En la figura, expresar OB y BC, en términos de x, y,
C
O A
a) OB xCos ySen
BC
xSen
yCos
b) OB xCos ySen
BC
ySen
xCos
c) OB xCos ySen
BC
xSen
yCos
d) OB xCos ySen
BC
yCos
xSen
e) OB xCos ySen
BC
xSen
yCos
B
OA = x
AC = y
35. En la figura: ABCD es un rectángulo inscrito en la
circunferencia de centro O, ARD ; RS // AB , AB=a.
Hallar el radio de la circunferencia.
B C
A
O
R
a) a 2Cos
b)
a
2Cos
c)
a
2Sen
d) aSen
e) a
1
Cos
2
S
D
36. Dado el cuadrado ABCD, se tiene que las áreas de los
triángulos FAE, EDC y CBF son iguales, luego Sen
es:
F
A B
a)
c)
e)
3 5
6
3
6
5
3 5
6
E
D
b)
d)
3 5
6
3 5
6
37. En la figura mostrada, son conocidos: , y h.
Entonces los valores de x e y son dados por:
a)
x
b) x
c)
x
2
h
Tan Tan
Tan
h
Tan
2
h
2 2
Tan Tan
; y
; y
; y
x
C
h
y
2
h Tan
Tan Tan
hTan
Tan Tan
2 2
h Tan
2 2
Tan Tan
2
2 2
d) x
h
; y
h Tan
2
2
( Tan Tan ) ( Tan Tan )
e) 2
x hTan Tan ; y h Tan Tan
38. En la siguiente figura, hallar (x + y) si:
AB = 3 y
AC
27
16
y
a) 5,14 b) 5,19 c) 5,29
d) 4,19 e) 3,19
x
A
B
C

39. De la figura hallar:
F
y
z
6Tanz
3Tany
CtgxTanyTa nz
k
k
x
a) 3,15 b) 2,35 c) 4,30
d) 3,00 e) 3,20
40. En un triángulo rectángulo BAC, se cumple que
2
CosBCosC .
4
Hallar la altura relativa a la hipotenusa sabiendo que
esta mide 6 2m
.
a) 2 m b) 3 m c) 3 m
d) 5 m e) 7 m
41. La figura muestra un cuadrado cuya área es 2
64 m y
tal que PC = BP'.
Hallar: AM
Si: AP = 6 m
6m
A B
M
P
12
a) 12 5 m b) 3 m
5
d)
12
5
5 m
O
P'
C D
e) 12 3 m
c)
16
5
3 m
42. En la siguiente figura, G es el baricentro del triángulo
ABC, AD = BD y 3Sen
Cos 3
Hallar la tangente del ángulo DCG.
B
A
a) 3
2
b)
3
3
d)
2
1
e)
2
G
D
1
c)
3
C
43. En la figura mostrada, calcular: E = Tanx Ctgy
Si: AB = AD = 1 ; DC = 2
1
a)
2
1
d)
4
A
1
b)
3
e) 1
B
x
y
D
c) 2
44. En la figura mostrada, ¿a qué distancia se encuentra el
globo respecto del lago?
H
Globo
Imagen
a) HCos 2 b) HSen2
c) HSec
2 d) HCsc2
e) HCtg
2
Lago
45. En la figura: DC = 2AB = 2.
Calcular el área del triángulo EFG.
a)
c)
e)
1
18
2
45
A
Tan
Tan
1
( Tan
9
B
Ctg
G
)
b)
d)
E
C
D
F C
2
Ctg
45
1
( Tan
18
Ctg
46. En un sector circular, cuyo ángulo central es , está
inscrito un cuadrado de lado L.
El radio de la circunferencia correspondiente es:
a)
L
2
Ctg
2
2
Ctg
2
5
1
2
)

)
c)
d)
e)
L
2
L
2
L
2
L
2
Ctg
2
Ctg
2
Ctg
Ctg
2
2
2
2
2
2
2Ctg
4Ctg
1
2
47. Se tiene un triángulo ABC en el que se conocen el lado
AC (opuesto al vértice B, de longitud b), y la bisectriz
de longitud w relativa al vértice B.
Hallar el área del triángulo ABC.
a)
b)
c)
d)
e)
b w
3
b w
2
b w
3
b w
2
b w
2
Cos
Cos
Cos
Cos
Cos
A C
3
A C
2
A C
2
A C
3
A C
4
48. Se tiene una poligonal ABCD tal que los ángulos ABC
5
y BCD miden
6
3
y
4
2
2
5
5
1
2
1
2
, respectivamente.
Hallar la longitud del radio de la circunferencia tangente
a los tres segmentos de la poligonal si cumple que :
2n
a)
m
d)
n
n
m
m
Ctg
5
Ctg
3
m y BC = n
12 8
n
b)
m
e) nm
n
c)
2m
49. En la figura, el triángulo NST es isósceles de base 6, KH
es el radio de la circunferencia circunscrita a un triángulo
equilátero de lado 6.
Hallar el radio R.
L
R
S
2
K N H T
a) 2 3Ctg
b) 2
4
c) 2 3Tan
d) 4
3
e) 2
3Ctg
3
3Tan
3Tan
50. En la figura mostrada se tiene un cuadrado ABCD con
uno de sus vértices en el origen de coordenadas cuyo
lado tiene la longitud a unidades. Si el segmento DM
divide al cuadrado en un triángulo y en un trapecio
cuyas áreas están en la relación de 1 : 4.
Calcule la tangente del ángulo MDC.
1
a)
4
3
d)
4
A B
D
2
b)
5
3
e)
5
1
c)
3
51. Dado un polígono regular convexo de n lados, se trazan
dos circunferencias, la primera de radio r que es
tangente a todos los lados del polígono, y la segunda
de radio R que pasa por todos sus vértices.
r
El valor de la razón es :
R
a) Sen
n
b)
Sen
2n
d) 1
Sen e) Cos
2 n n
c)
C
4
M
4
Sen
2
n
52. Un cuadrado MNPQ cuyos lados miden 2 2
está inscrito en una circunferencia.
Calcular la distancia del punto Q al punto medio del
arco MN.
a) 0, 5 b) 1 c) 1,
5
2
d) 2 e)
2
,

53. En la siguiente figura:
A
4r
2
La relación 2
c
B
O
r
c
es equivalente a:
a) 2 1 Cos b) 2 1 Cos
2
c) 2 1 Sen d)
e) 2 ( 1 - Cos )(1 - Sen )
2
1
Cos
2
54. La siguiente figura es un cuadrado, donde Q es punto
medio del lado AB.
Determine Csc
A
Q
B
a) 2
5
b)
4
d) 4 e) 2 5
55. En la figura, hallar "x":
x
C D
c) 3
a) kSec Sen
5 b) kSec Tan
6
c) kCtg
7
Sec d) kTan
6
Cos
e) kSec Cos
5
56. En el cuadrado ABCD, las áreas de los triángulos OAP,
PDC y CBO son iguales.
Luego Csc es:
k
O
A B
P
C D
C
a)
c)
e)
6
3 5
6
3 5
6
3 5
b)
d)
6
5 3
6
3 5
57. En la figura hallar el valor de "h" en función de , y
a)
c)
e)
. Si : c , Â , B ˆ
Ctg
C
A D
B
Ctg
Sen
Sen Sen
Cos
Sen
b)
d)
Tan
Ctg
h
Tan
Ctg
58.En En un triángulo ABC, recto en B, la mediana CM y el
cateto BA forman un ángulo agudo . Entonces, Tg
es:
a) 2 TanA b) 2 CtgA
c) 2TanC d) TanA + TgC
e) 2(TanC + CtgA)
59. En la semicircunferencia mostrada, halle:
K
Sen2
Sen2
3
Q
C
1
A O P B
a) 2 b) 3 c) 4
1
d)
4
1
e)
3

60. Del gráfico, hallar Tan
Si:
AP
m
PB
n
A
M
P N
O B
a)
c)
e)
m
n(
2m
n
m(
2n
2n
m
2m
n
n)
m)
b)
d)
n
m(
2m
2m
n
2n
m
n)

Claves
Claves
b
a
c
c
b
d
a
a
a
d
c
c
d
b
b
c
c
c
c
a
b
e
b
c
d
c
d
c
d
e
a
a
c
b
d
b
e
b
b
d
c
d
c
a
c
b
b
b
b
b
e
b
e
b
b
d
a
a
c
c
01.
02.
03.
04.
05.
06.
07.
08.
09.
10.
11.
12.
13.
14.
15.
16.
17.
18.
19.
20.
21.
22.
23.
24.
25.
26.
27.
28.
29.
30.
31.
32.
33.
34.
35.
36.
37.
38.
39.
40.
41.
42.
43.
44.
45.
46.
47.
48.
49.
50.
51.
52.
53.
54.
55.
56.
57.
58.
59.
60.
4

ÁNGULOS VERTICALES
Son aquellos ángulos ubicados en un plano vertical que, en la práctica, son formados por una línea visual (o línea de mira)
y una línea horizontal, como resultado de haberse efectuado una observación. Estos resultados se clasifican en: ángulos de
elevación y ángulos de depresión.
(ver gráficos).
h
Línea Horizontal
: Ángulo de Elevación
Consideración: En el gráfico adjunto, " " es
el ángulo bajo el cual se divisa la torre. Note
que deben trazarse las dos visuales; una hacia
la parte alta y la otra hacia la parte baja.
Luego " " es el ángulo formado por las dos
visuales.
ÁNGULOS HORIZONTALES
H
Línea Horizontal
: Ángulo de Depresión
Son aquellos ángulos ubicados en un plano horizontal que, en la práctica, los vamos a ubicar en la Rosa Náutica.
Rosa Náutica: (compás marino), es un instrumento de orientación que permitirá localizar una ciudad, persona o punto;
respecto de una referencia, mediante el uso de las direcciones :
B
40º 30º
Oeste (O) P
Este (E)
42º Referencia
C
Norte (N)
Sur (S)
Capítulo
3
A
ÁNGULOS VERTICALES
ÁNGULOS HORIZONTALES
Note que dichas direcciones en este caso para A;
B y C; forman con los ejes principales ciertos
ángulos; con quienes se van a denotar dichas
direcciones.
Por ejemplo:
"A" se halla el E30ºN de "P"
"B" se halla al O40ºN de "P"
"C" se halla al S42ºO de "P"

Note que dichas direcciones en este caso para A; B y C; forman con los ejes principales ciertos ángulos; con quienes se van
a denotar dichas direcciones.
Por ejemplo:
"A" se halla el E30ºN de "P" .
"B" se halla al O40ºN de "P" .
"C" se halla al S42ºO de "P" .
O
Q
30º
R
S
N
24º
10º
66º
P
S
E
P
Q
S
Está al N24º E de " R"
Está al E66º N de " R"
Está al O30º N de " R"
Está al
Está al S10º E
Está al
de " R"
de " R"
de " R"
Ahora bien, algunas direcciones tienen la particularidad de obtenerse trazando bisectrices sucesivas, a partir de los ejes
principales; por lo que su notación será también particular. Indicaremos lo que ocurre entre el Norte y el Este, y usted
concluye los restantes por analogía.
O S E O
S
En cualquiera de los casos : 11º 15'
ó rad
16
O
N N
N1
NE
N N
E
O
S S
4
NNE
NE 1N
4
NE
E
4 1 NE
ENE
E 1 NE
4
E
E

SITUACIONES COMBINADAS
Cuando los enunciados de los problemas mencionan ángulos verticales (de elevación o de depresión) y ángulos horizontales
(uso de direcciones, generalmente), al mismo tiempo, la rosa náutica a emplear asume una posición más real; es decir,
ubicada en un plano horizontal. Por ejemplo, grafiquemos la siguiente situación:
"Desde un punto en tierra, se divisa al Norte lo alto de un poste con un ángulo de elevación " ". Si luego nos desplazamos
hacia el N60ºE, hasta ubicarnos al Este del poste, el ángulo de elevación para su parte más alta sería " ". Ahora, note la
representación gráfica:
60º

01. Desde un punto de tierra se observa lo alto de un edificio
con ángulo de elevación 37º, si la visual mide 30 m,
determinar la altura de edificio.
a) 3 m b) 12 c) 15
d) 18 e) 24
02. Una persona de 2 m de estatura divisa lo alto de un
poste con un ángulo de elevación de 45º. Si la altura
del poste es de 20 m. ¿A qué distancia de el se halla la
persona?
a) 18 b) 20 c) 22
d) 24 e) 32
03. Desde un punto ubicado a 24 m de una torre, se divisa
su parte más alta con un ángulo de elevación de 53º.
¿Cuál es la altura de la torre?
a) 24 b) 36 c) 32
d) 42 e) 48
04. Desde un punto en tierra se divisa lo alto de un poste
con un ángulo de elevación de 37º. Si la altura del
poste es de 30 m. ¿A qué distancia del poste se
encuentra el punto de observación?
a) 10 b) 20 c) 30
d) 40 e) 50
05. Desde dos puntos separados 42 m se observa la parte
alta de un farol que se encuentra entre ellos con ángulos
de elevación 37º y 45º. Determinar la altura del farol.
a) 9 b) 10 c) 11
d) 12 e) 13
06. Desde un muro de 6 m de altura se observa la parte
alta y baja un poste con ángulos de elevación y
depresión 60º y 30º respectivamente. Determine la
altura del poste.
a) 15 m b) 24 c) 30
d) 36 e) 48
07. Desde un punto en tierra se ve lo alto de una torre con
un ángulo de elevación " " (Tg =1/4). ¿A qué
distancia de la torre se halla el punto de observación, si
la altura de la torre es 7 m?
a) 14 b) 28 c) 56
d) 21 e) N.A.
08. Desde un punto en tierra se divisa lo alto de un poste
con un ángulo de elevación de 37º. Si nos acercamos
una distancia igual a la altura del poste, el ángulo de
elevación es " ". Calcular: "Tg ".
a) 1 b) 2 c) 3
d) 4 e) 6
EJERCICIOS PROPUESTOS
09. Desde un punto ubicado a 15 m de un poste se ve su
parte más alta con un ángulo de elevación de 53º.
Caminamos 3 m en dirección al poste y el ángulo de
elevación para su parte más alta es " ". Calcular:
"Ctg ".
a) 1 b) 2 c) 3
d) 4 e) 6
10. Una hormiga observa la copa de un árbol con un
ángulo de elevación de 37º, luego se acerca 7 m y
observa el mismo punto con un ángulo de elevación
de 53º. Calcular la altura del árbol.
a) 10 b) 12 c) 14
d) 16 e) 20
11. Desde dos puntos separados 52 m se observa lo alto
de un poste con ángulos de elevación 53º y
Tg
2
. Si el poste se encuentra entre los dos
5
puntos. Determine su altura.
a) 12 m b) 16 c) 18
d) 9 e) 11
12. Se observa un poste con ángulo de elevación " " nos
acercamos "L" y el ángulo de elevación es 45º. Si la
altura de poste es "2 L". Determinar: Tg .
a) 1/3
b) 2/3 c) 1
d) 1/2 e) 3/2
13. Desde un edificio de 12 m de altura se observa un
automóvil con ángulo con ángulo de depresión " "
Tg
1
. Luego se observa una señal más cerca del
3
edificio con ángulo de depresión 45º. Determine la
distancia entre la señal y el automóvil.
a) 12 m b) 18 c) 24
d) 36 e) 10
14. Desde un punto en tierra se divisa lo alto de un poste
con un ángulo de elevación de 45º, y desde otro punto
ubicado en la mitad de la distancia que hay entre el
primer punto y el poste, el ángulo de elevación es " ".
Calcular: "Tg ".
a) 2 b) 4 c) 6
d) 8 e) 16
15. Desde un punto ubicado a 30 m de una torre se divisa
su parte más alta con un ángulo de elevación " "
(Tg =1/3). Si nos alejamos una distancia igual a la
altura de la torre, el ángulo de elevación es " ".

Calcular: "Ctg ".
a) 1 b) 2 c) 3
d) 4 e) 6
16. Desde las partes superiores del primero, segundo y
tercer piso de un edificio se observa lo alto de otro
edificio con ángulos de elevación , , , respectiva-
mente. Si: Tg -Tg = 0,1 y Tg =2,7. ¿Cuántos pisos
tiene el segundo edificio?
a) 10 b) 15 c) 20
d) 30 e) 40
17. Desde lo alto de un edificio de 8 pisos, se ve un punto
en tierra con un ángulo de depresión de 45º. Cuánto
mide cada piso del edificio, si el punto observado se
halla a 24 m del mismo?
a) 2 b) 2,5 c) 3
d) 3,5 e) 4
18. Desde un punto ubicado a 36 m de un edificio de 28 m
de altura, se divisa su parte más alta con un ángulo de
elevación de 53º. Señale la distancia de un punto a la
base del edificio.
a) 20 b) 21 c) 35
d) 32 e) 49
19. Desde el puesto del vigía de un barco que tiene 48 m
de altura se observa que el ángulo de depresión de un
bote es de 30º. Calcular la distancia a la que esta el
barco.
a) 48 b) 48 3 c) 12
d) 24 e) 6 3
20. Desde el pie de un poste se observa la parte más alta
de una torre con un ángulo de elevación de 45º, el
mismo punto es observado desde la parte más alta del
poste con un ángulo de elevación de 37º. Calcular la
longitud del poste si la distancia entre el poste y la torre
es de 120 m.
a) 10 b) 15 c) 20
d) 30 e) 40
21. Desde un punto en Tierra se ve lo alto de un poste con
un ángulo de elevación " " ( Tan
1
) ; y si nos
6
acercamos 30 m el ángulo de elevación es de 45º.
¿Cuál es la altura del poste?
a) 5 m b) 6 m c) 4 m
d) 8 m e) 12 m
22. Un móvil se desplaza hacia una torre con una velocidad
de 4 m/min; y en un primer momento, observa su parte
más alta con un ángulo de elevación de 37º. Si la torre
mide 192 m, ¿después de qué tiempo el ángulo de
elevación tiene como tangente 8?
a) 29 min b) 48 min c) 1h 12 min
d) 1h 18 min e) 58 min
23. Un niño observa los ojos de su padre con un ángulo
de elevación , y su padre observa sus pies con un
ángulo de depresión ( 90º
) .
Obtener la relación entre sus alturas.
a) 1
2
Tan b) 1
2
Tan
c) 1
2
Cot d) 1
2
Cot
e) Tan 1
2
24. Se tiene una torre en el borde de un acantilado; cuyas
partes alta y baja son vistas desde un punto de la
superficie horizontal con ángulos de elevación " " y
" ", respectivamente ( 3Tan
4Tan
) . La altura del
acantilado es de 212,31 m.
¿Cuál es la altura de la torre?
a) 141,54 m b) 28,308 m
c) 159,2325 m d) 70,77 m
e) 35,385 m
25. Subiendo por un camino inclinado, de ángulo " "
respecto a la horizontal; se observa lo alto de una torre
con un ángulo de elevación " 2 "; verificándose que la
torre mide 3 m y la visual 7 m.
¿Cuál es el valor de " Tan "?
3
a)
7
4
d)
7
6
b
7
2
e)
7
3
c)
14
26. Desde dos puntos ubicados al Sur y al Oeste de una
torre de 24 m de altura, se ve su parte más alta con
ángulo de elevación de 45º y 37º respectivamente.
¿Cuál es la distancia entre los puntos de observación?
a) 32 m b) 36 m c) 56 m
d) 48 m e) 40 m
27. Desde dos puntos ubicados al Sur y Oeste de un poste,
se divisa su parte más alta con ángulos de elevación
" " y " 90 º ", respectivamente. Si la distancia entre
los puntos de observación es el doble de la altura del
poste, calcular: P Tan Cot
a) 3 b) 2 3 c) 6
d) 2 6 e) 3 2

28. El ángulo de elevación de la cúspide de una torre es de
60º a 72 metros de ella. Estando el ojo del observador
a 3 metros sobre el suelo, la altura de la torre es
aproximadamente.
a) 72 m b) 73 3 m c) 71 m
d) 73 m e) 72 3 m
29. Desde el pie de un poste el ángulo de elevación de la
parte más alta de un campanario es 45º. Desde la parte
superior del poste que tiene 9 m de altura, el ángulo de
elevación es de 30º.
¿Cuál es la altura del campanario?
a)
d)
9
3
2
9 3
3 1
b)
e)
7
1
2
2
9 3
3 1
c)
5 3
3 1
30. Un niño está volando su cometa soltándole cuerda, la
misma que se mantiene tensa y haciendo un ángulo
con la horizontal. A 120 m detrás del niño hay un
hombre. Cuando la cometa se encuentra a 20 m de
altura, el hombre la observa con un ángulo respecto
a la horizontal.
¿A cuántos metros de altura se encontrará la cometa
para que sea observada por el hombre con un ángulo
2 ?
Considere :
a)
637
23
d)
1561
19
Tg
1
3
b)
1285
17
e)
637
13
1080
c)
13
31. Una balsa se aproxima hacia un faro. En un
determinado instante, el faro es observado por el
tripulante de la balsa con un ángulo de elevación de
. Al recorrer 36m adicionales vuelve a observar,
12
encontrando esta vez un ángulo de 6 .
Encuentre la altura del faro (desprecie la altura del
tripulante que hizo la observación)
a) 10 m b) 15 m c) 12 m
d) 14 m e) 18 m
32. Desde lo alto de un edificio se observa a un automóvil
con un ángulo de depresión de 37º. Dicho automóvil
se desplaza con velocidad constante. Luego que avanza
28 m acercándose al edificio es observado con un
ángulo de depresión de 53º. Si desde esta posición
tarda en llegar al edificio 6 segundos, calcular la
velocidad del automovil.
a) 3 m/s b) 6 m/s c) 7 m/s
d) 12 m/s e) 4 m/s
33. Un avión se encuentra volando horizontalmente a 180
km/h. En cierto instante, el piloto ve una señal en tierra
con un ángulo de depresión de 30º. Dos minutos
después, estando sobre la señal, el piloto observa a
una distancia de 1000 metros un aerostato con un
ángulo de elevación de 60º.
¿A qué altura está volando el aerostato en ese instante?
a) 2 3 km b) 2, 5 3 km c) 3 3 km
d) 3, 5 3 km e) 4 3 km
34. Un barco y un avión viajan en la misma dirección y en
el mismo sentido. En la primera observación desde el
barco se ve al avión adelante con un ángulo de
elevación de 53º, marcando con una boya dicho lugar.
En la segunda observación se le ve con un ángulo de
37º, si la velocidad del avión es 8 veces la del barco.
Calcular la cotangente del ángulo con la que el avión
en la segunda posición observa la boya.
17
a)
12
3
d)
4
15
b)
11
5
e)
7
11
c)
17
35. Dos puntos están ubicados en un mismo nivel del suelo.
Desde uno de ellos se observa el extremo superior de
un poste con un ángulo de elevación y desde otro
punto se observa el punto medio del poste con un
ángulo de elevación . Si la suma de las distancias del
poste a cada uno de los puntos es d, calcular la altura
del poste.
a) dTan 2dTan
b)
c) 2dCtg dCtg d)
e) d(
Tan 2Tan
)
2Tan
2Ctg
2d
2d
Tan
Ctg
36. Dos autos parten simultáneamente desde un punto "P"
en direcciones que forman un ángulo " " uno a
5 km/h y el otro a 12 km/h.
Calcular el Cos sabiendo que al cabo de una hora la
distancia desde el punto "P" al punto medio del
segmento que separa ambos autos es de 7 km.
5
a)
8
9
d)
40
7
b)
16
13
e)
25
3
c)
80

37. Un niño de estatura "h" está parado sobre la banca y
observa los ojos de su padre; de estatura "H", con un
ángulo de elevación " " y sus pies con un ángulo de
depresión " ". Si el padre divisa los pies de su hijo
con un ángulo de depresión " ".
H
Hallar:
h
a)
c)
e)
Tan
Tan
Tan
Tan
Tan
Tan
Tan
Tan
Tan
Tan
Tan
Tan
b)
d)
Tan
Tan
Tan
Tan
Tan
Tan
Tan
Tan
38. Desde la parte superior del tercer piso de un edificio de
9, se ve un momento de menor altura, con un ángulo
de elevación "x", su parte más alta y un ángulo de
depresión "y" su base. Si desde lo alto del edificio, la
tangente del ángulo de depresión con la que se ve la
base del monumento, es sextuplo de la tangente del
ángulo con que se ve la parte más alta.
Calcular: E= 4Coty · Tanx
a) 2 b) 4 c) 5
d) 8 e) 6
39. Desde lo alto de un edificio se ven tres puntos en Tierra,
a un mismo lado, con ángulos de depresión , 45º y
90 º ( 45º
) . Si el punto intermedio dista del
más alejado, el doble del más cercano, calcular:
N
6Tan
a) 1 b) 3 c) 5
d) 7 e) 9
2
Cot
40. Un poste, una persona y una torre están ubicados del
modo que se mencionan y sus alturas están en la
proporción 3; 1; 5. Si de lo alto del poste se divisa lo
alto de la persona con un ángulo de depresión " ";
mientras que la persona divisa lo alto de la torre con un
ángulo de elevación , desde lo alto de la torre se ve
la base del poste con un ángulo de depresión " ". Si
se verifica que:
Cot
Calcular: K = m + 2n
mCot
a) 1 b) 2 c) 3
d) 4 e) 5
nCot
41. Se tiene un poste PQ ("P" en el suelo) y tres puntos en
la superficie horizontal A, B y C, perfectamente
alineados; desde los cuales se ve "Q" con ángulos de
elevación , y respectivamente. Si BP es bisectriz
del ángulo PC ˆ A que mide 60º, calcular:
J
Tan Tan
Tan
a) 2 b) 2 3 c) 3
3
d) 3 e)
3
42. Desde la parte más alta de un árbol de 5 metros de
altura se observa a otros dos de 1 metro y 4 metros de
altura con ángulos de depresión y ( 90º
) , si estos
están al Este y al Sur del árbol más alto, respectivamente.
Calcular: " Tan ", si además desde la parte más alta del
árbol más pequeño, se observa la parte más alta del
árbol de 4 metros con un ángulo de elevación de
( 90º
)
1
a) 4 2
b)
1
2
d) 2 e) 2 2
c) 4 2
43. Un barco se encuentra al Sur de un helicóptero, el barco
permanece inmóvil; pero el helicóptero avanza cierta
distancia hacia el Este. Desde el barco se observa al
helicóptero en la segunda posición con un ángulo de
elevación " ". Si el ángulo de elevación en la primera
posición es de 45º y el helicóptero avanzó 2km, calcular
" ", si además el helicóptero se encuentra a una altura
de 2 km .
1
a)
ArcTan
2
b) ArcTan
1
3
3
c) ArcTan
4
e) 45º
d) 30º
44. Se tienen tres puntos en tierra A, B y C (AB = BC); y un
poste PQ ("Q" en el suelo, al interior del triángulo ABC),
desde los cuales se ve lo alto del poste con ángulos de
elevación , y respectivamente.
Si : QC y ˆ
QB x B
ˆ A
Señale el equivalente de:
J
Cot Cosx
Cot
2
Cot Cosy
Cot
2
a) Tan b) 2Tan c) 2Cot
1
d) Cot
2
1
e) Tan
2
45. Luciano observa a Luciana en la dirección NE y a
18 2 m de distancia; a su vez Luciana observa a Lucio
en la dirección E37ºS.
Determine la distancia que separa a Luciano y a Lucio,
si Lucio se encuentra al Este de Luciano.

a) 41 m b) 40 m c) 24 m
d) 18 m e) 42 m
46. Desde una ciudad "A" se divisan a otras dos "B" y "C"
en las direcciones O80ºN y E40ºN, respectivamente.
Además desde "B" se divisa a "C" al E50ºS a una
distancia de 173 km.
¿Cuál es la distancia entre "A" y "B"?
a) 100 km b) 200 km c) 150 km
d) 273 km e) 300 km
47. ¿Cuál es la dirección de la bisectriz del menor ángulo
formado por las direcciones N20ºE y S80ºO?
a) N10ºO b) N20ºO c) N30ºO
d) N40ºO e) N50ºO
48. Calcular el menor ángulo que forman la bisectriz de SO
y SO
1
S con la bisectriz de SE y SE
1
S
4
4
a) 50º b) 78º45' c) 77º
d) 67º30' e) 90º
49. Se tiene una torre en el borde de un acantilado, cuyas
partes alta y baja son vistas desde un punto de la
superficie horizontal con ángulos de elevación " " y
" " respectivamente ( 3Tan
4Tan
) . La altura del
acantilado es de 212,31 m.
¿Cuál es la altura de la torre?
a) 141,54 m b) 28,308 m
c) 159,2325 m d) 70,77 m
e) 35,385 m
50. Una persona camina 5 2 (aprox.) al norte de su casa,
luego 13 m en la dirección S E , si ahora se encuentra
en la dirección NE de su casa.
Hallar: Csc
13
a)
5
d)
10 2
13
b)
13 2
17
13
e)
17
17
c)
13
51. Desde dos puntos A y B, situados al Oeste y al Norte de
una torre, se observa la parte más alta de ésta con
ángulos de elevación y , respectivamente; y desde
el punto medio de AB, el ángulo de elevación es " ".
Calcular: Tan Cot
3
a)
2
d) 2 e) 2 3
b) 1 c) 3
52. Un niño sostiene dos globos. El ángulo de elevación
que tiene en la mano derecha es de 21º y la cuerda
mide "a" metros. El ángulo de elevación del globo que
sostiene en la mano izquierda es de 24º y la cuerda
mide a 2 metros.
¿Cuál es la distancia que hay entre los globos?
a) ( 1 2)
a metros b) ( 2 2)
a metros
c) 2a 5 a metros d) a 5
e) ( 2 5)
a metros
a metros
53. "Moshé" divisa los ojos de su padre con un ángulo de
elevación " " y sus pies con un ángulo de depresión
" "; mientras que su padre divisa los pies de "Moshé"
con un ángulo de depresión " ". Sabiendo que las
estaturas de "Moshé" y su padre son "h" y "H"
respectivamente, señale el equivalente de:
Cot Cot
a)
Cot
2
c)
e)
Cot
Tan
Cot
Tan
Cot
Tan
J
b)
H
h
Cot
Cot Cot
2
h
H
Cot
d) Cot Cot
54. Desde un punto en tierra, se divisa lo alto de un poste,
con un ángulo de elevación de 10º. Nos acercamos
una distancia " d
1 " y el ángulo de elevación es de 40º;
y si nos desplazamos una distancia " d
2 " hasta
ubicarnos al otro lado del poste, el ángulo de elevación
es de 20º.
d
1
Calcular:
d
2
(Sug. Cos10º = 0,9848)
a) 1,137 b) 1,232 c) 1,321
d) 0,957 e) 0,352
55. Un observador divisa un poste vertical bajo un ángulo
" " notando que sus visuales son iguales. Se acerca
una distancia igual a las dos terceras partes de la
distancia que inicialmente lo separaba del poste y divisa
a éste. ahora bajo un ángulo " ".
Calcular "n" en la igualdad.
Sen
Sen
a) 1 b) 2 c) 3
d) 4 e) 5
2
nSen
2
2
Sen
2

56. Una persona camina, por un camino inclinado que
forma un ángulo "x" con la horizontal y observa la parte
superior de una torre con un ángulo de inclinación
"2x". Luego de caminar una distancia de 15 veces la
altura de la torre, observa nuevamente su parte superior
con un ángulo de elevación de "3x".
Calcular: E = Cscx - 15
a) 10 b) 20 c) 12
d) 15 e) 25
57. Se tiene una torre y dos puntos A y B ubicados en
lados opuestos de ella. Desde "A" se divisa un punto
de la torre con un ángulo de elevación " "; notándose
que la distancia de dicho punto observado a lo alto de
la torre es igual a la visual trazada para dicha
observación; mientras que, desde "B", se divisa un punto
ubicado 1 m, más abajo que al anterior con un ángulo
de elevación " " . Notándose que la visual trazada es
igual a la distancia del nuevo punto observado a lo alto
de la torre, hallar la altura de la torre.
a)
b)
c)
d)
e)
( Tan 1)(
Tan
Tan Tan
( Sen
( 1
Sen
1)(
Sen
Sen
1)
1)
Sen )( 1 Sen )
Sen Sen
( Cos 1)(
Cos
Cos Cos
( Tan 1)(
Tan
Tan Tan
1)
1)
58. Desde cuatro puntos colineales de la superficie A, B, C
y D se divisa lo alto de una torre PQ ("Q" en el piso)
con ángulos de elevación
mente.
, , y respectiva-
Si: QD 10º
ˆ QC C ˆ QB B ˆ A y
Sen 10º
0,
173648 .
Calcular:
J
Tan Tan
Tan Tan
Tan
Tan
a) 1,1983 b) 2,2343 c) 1,7124
d) 2,5783 e) 2,8794
Tan
Tan
59. Desde un punto del suelo, ubicado al O30ºS de una
torre, se divisa su parte más alta con un ángulo de
elevación 53º. De esta ubicación nos desplazamos al
S30ºE hasta ubicarnos al Sur de la torre. Observaríamos
su parte más alta con un ángulo de elevación " ".
Calcular: Tan
1
a)
3
3
d)
2
2
b)
3
1
e)
4
3
c)
4
60.Un reflector situado al ras del suelo ilumina un
monumento bajo un ángulo de 30º. Si trasladamos el
reflector 2 m más cerca del monumento, éste se ve bajo
un ángulo de 45º.
¿Cuál es la altura (y) del monumento y cuál es su
distancia (x) al segundo lugar de iluminación?
a)
b)
c)
d)
y
y
y
y
2 3
3 3
2 3
3 3
2 3
3 3
2 3
3 3
;
;
;
;
x
x
x
x
2 3
3 3
2 3
3 3
2 3
3 3
2 3
3 3
e) y 3 3 ; x 3 3

Claves
Claves
d
a
c
d
e
b
b
c
a
b
b
b
c
a
d
b
c
e
b
d
b
e
b
b
a
e
c
b
d
c
e
b
b
a
b
c
b
e
d
c
c
c
d
e
e
b
d
b
d
b
c
d
c
a
c
d
b
e
b
c
01.
02.
03.
04.
05.
06.
07.
08.
09.
10.
11.
12.
13.
14.
15.
16.
17.
18.
19.
20.
21.
22.
23.
24.
25.
26.
27.
28.
29.
30.
31.
32.
33.
34.
35.
36.
37.
38.
39.
40.
41.
42.
43.
44.
45.
46.
47.
48.
49.
50.
51.
52.
53.
54.
55.
56.
57.
58.
59.
60.

Capítulo
4
SISTEMA COORDENADO RECTANGULAR
SISTEMA COORDENADO RECTANGULAR
Denominado también cartesiano, en honor al matemático René Descartes (1596-1650).
Se determina trazando dos rectas numéricas perpendiculares entre sí que se intersectan en un punto "O" y divide al plano en
cuatro semiplanos denominados cuadrantes.
* La recta horizontal se llama eje "x" o eje de abscisas.
* La recta vertical se llama eje "y" o eje de ordenadas.
* El punto "O" se denomina origen de coordenadas.
Q( x ;y )
2 2
Distancia entre dos puntos del plano cartesiano
Sean P ( x ; y )
1 1 1
y P ( x ; y )
2 2 2
dos puntos del
plano cartesiano, entonces la distancia "d" entre
los puntos
d
* Radio Vector
P y
1
( x
y
Cuadrante II Cuadrante I
y
1
P( x ;y )
1 1
x 2
P está dada por:
2
2
2
x
1
)
( y
2
O (0;0)
y
2
Cuadrante III Cuadrante IV
2
y
1
)
Es la distancia del origen de coordenadas a un punto
cualquiera del plano cartesiano.
Si: P(
x ; y ) es un punto del plano cartesiano el radio
0 0
vector se calcula así:
r
x
2
0
y
2
0
y
y 2
y 1
x 1
P ( x ;y )
1 1 1
y
y 0
x 1
r
d
x
x 2
x 0
P ( x ;y )
2 2 2
x
P( x ;y )
0 0
x

División de un segmento en una razón dada:
Sea P ( x ; y ) un punto cualquiera sobre un segmento de
0 0 0
extremos P ( x ; y ) y P ( x ; y ) tal que:
1 1 1 2 2 2
Las coordenadas de
x
0
ax
2
a
P
1
P
0
P
0
P
2
P
0
son:
bx
1
b
Punto Medio de un Segmento
a
( razón)
b
y
0
ay
2
a
by
1
b
Las coordenadas del punto medio M del segmento de
extremos P ( x ; y )
1 1 1
y P ( x ; y ) se calcula así:
2 2 2
x
0
y
0
x
1
x
2
2
y y
1 2
2
Coordenadas del baricentro de un triángulo:
En el triángulo cuyos vértices son A(
x ; y ) ;
1 1
B(
x ; y )
2 2
y
C(
x ; y ) , las coordenadas del baricentro están dadas por:
3 3
G: baricentro
G
x
1
x
2
3
x y
3 ; 1
Área de una región triangular:
y
2
3
y
3
y
y
y
a
P ( x ;y )
1 1 1
P ( x ;y )
1 1 1
A( x ;y )
1 1
b
P ( x ;y )
0 0 0
M( x ;y )
0 0
C( x ;y )
3 3
G
P ( x ;y )
2 2 2
P ( x ;y )
2 2 2
x
x
B( x ;y )
2 2
Para calcular el área "S" de una región triangular, se colocan las coordenadas de uno de los vértices y seguimos el sentido
antihorario hasta cerrar la figura y volver a colocar el primer vértice escogido, finalmente, se procede como a continuación se
indica.
y
A( x ;y )
1 1
C( x ;y )
3 3
S
B( x ;y )
2 2
x
x
1
x y
2 1 x
2
x
3
y
2 x
3
x
1
y
3
x
1
B
Luego :
S
y
1
y
2
y
3
x y
1 2
x
2
y
3
y
1
x
3
y
1
A
A B
2
x

01. Determine el radio vector de (2,-3).
a) 5 b) 11 c) 13
d) 17 e) 19
02. Determinar el radio vector de ( 2,
7 )
a) 3 b) 10 c) 3
d) 4 e) 5
03. Determinar el radio vector del punto medio del
segmento formado al unir los puntos (3,1) y (7,9).
a) 5 b) 2 5 c) 5 2
d) 10 e) 15
04. Si: (-1,2) es el punto medio del segmento formado al
unir los puntos, (-3,-1) y (a,b). Determinar: "a+b".
a) 3 b) 4 c) 5
d) 6 e) 7
05. Del gráfico, calcular: "d".
(-11,1)
d
(3,5)
a) 37 b) 41 c) 53
d) 61 e) 82
EJERCICIOS PROPUESTOS
(5,2)
06. Dos vértices consecutivos de un cuadrado son (-7,3) y
(-1,-5), determine su perímetro.
a) 60 b) 40 c) 20
d) 12 3 e) 15 2
07. Se tiene una circunferencia de centro (-3,7) que pasa
por (2,-5), determinar su diámetro.
a) 13 b) 15 c) 26
d) 30 e) 35
08. Si: (4,2) es el punto medio del segmento formado al
unir los puntos (a,-3) y (5,b). Determinar: E b a
a) 2 b) 3 c) 2
d) 3 e) 5
09. Determine el producto de las coordenadas del punto
del segmento formado al unir los puntos (-7,3) y (1,5).
a) 6 b) -6 c) 12
d) -12 e) 15
10. Al unir los puntos A(-5,1), B(-1,7) y C(5,-1). Se forma
un triángulo ABC. Determine la longitud de la mediana
AM , (M en BC ).
a) 47 b) 51 c) 53
d) 57 e) 61
11. Determine las coordenadas del baricentro de un
triángulo que se forma al unir los puntos. A(-1,5); B(3,9)
y C(7,1).
a) (3,2) b) (-7,3) c) (3,5)
d) (5,3) e) (-3,5)
12. En el gráfico, hallar "x+y":
K
A(-2;3)
P
2K
a) (2,3) b) (2,4) c) (1,3)
d) (-1,2)
e) (-2,4)
13. Según el gráfico, halle "p":
A(1;9)
2S 3S
B(10;6)
B(-2;5) C(8;10)
a) (1,8) b) (2,7) c) (3,5)
d) (3,7) e) (4,6)
14. Los vértices de un triángulo son A(3,1); B(9,1) y C(3,7).
Determine su área.
a) 36
2
d) 16 2
b) 18 2
e) 9 2
c) 24 2
15. Los vértices de un triángulo son A(1;2), B(3;6) y
C(-1,0). Calcular la longitud de la mediana relativa al
lado AB .
a) 2 b) 3 c) 4
d) 5 e) 6

16. Determine en el eje "x" un punto que tenga una
distancia de 5 unidades del punto (2,4).
a) (-1,0) b) (1,0) c) (5,0)
d) (6,0) e) a y c
17. Si ABCD es un paralelogramo donde A(3,2), B(1,5),
C(-2,3). Halle el punto D.
a) (0,0) b) (1,7) c) (-1,3)
d) (-2,2) e) (-5,1)
18. Los puntos A(4,-2); B(1,2) y C(5,5) son los vértices de
un triángulo:
a) Isósceles. b) Equilátero.
c) Rectángulo. d) Rectángulo Isósceles.
e) Oblicuángulo.
19. Hallar en el eje de ordenadas un punto A cuya distancia
hasta el punto B(-8,13) sea igual a 17.
a) (0,-1) b) (0,-2) c) (1,2)
d) (2,8) e) (0,-28)
20. Si P(a;a+1) es un punto que equidista de A(2,1) y
B(-6,5). Hallar el valor de "a".
a) 6 b) -6 c) 0
d) 1 e) -1
21. Se tienen dos vértices opuestos de un cuadrado (-5,8)
y (1,2); determinar su centro de gravedad.
a) (-1,3) b) (-2,3) c) (-2,5)
d) (-1,5) e) (1,3)
22. El centro de una circunferencia es (-4, 5 ), determinar
su área si pasa por el origen de coordenadas (usar:
(
22
) .
7
a) 2
2
d) 66 2
b) 3 2
e) 81 2
c) 44 2
23. Si P es punto medio de MN ; M y N son puntos medios
de AC y BC respectivamente, determine el radio vector
del punto P; siendo A(-4,5); B(2,5) y C(6,-3).
a) 7 b) 10 c) 2 3
d) 3 2 e) 15
24. Si (-5,3) es punto medio entre (x,0) y (0,y); calcular:
E y x .
a) 2 b) 3 c) 4
d) 5 e) 6
25. Hallar las coordenadas de un punto "A" cuya distancia
al origen es igual a 13u; sabiendo además que su
ordenadas tiene 7u más que su abcisa.
(Dar la suma de coordenadas).
a) 17 b) 16 c) -17
d) a y b e) a y c
26. Si (2,3) es el punto medio del segmento AB siendo
A(-3,5) y B(a,b). Calcular: a+b.
a) 5 b) 6 c) 7
d) 8 e) 9
27. El segmento que une A=(-2,1) con B=(2,2) se
prolonga hasta C sabiendo que BC=3AB. Hallar las
coordenadas de C.
a) (14,11) b) (11,14) c) (1,7)
d) (14,-11) e) (-14,11)
28. Si un vértice de un triángulo ABC, es A=(1,3) y el
baricentro del triángulo es G=(3,1). ¿Cuál es la suma
de coordenadas del punto medio "M" opuesto al vértice
"A"?
a) 1 b) 2 c) 3
d) 4 e) 5
29. Dados dos vértices consecutivos de un cuadrado
A(3 ; 7) y B( 1 ; 4), calcule su área.
a) 127
2
b) 137
2
c) 147
2
d) 81
2
e) 100
2
30. Señale las coordenadas del punto "P" ubicado en el eje
de abscisas que equidista de A(1 ; 5) y B(7 ; 3)
a)
d)
7
; 0
3
11
; 0
2
b
e)
8
; 0
3
11
; 0
4
c)
4
; 0
3
31. En un triángulo ABC, los vértices son A(3 ; 1), B(1 ; 5)
y C( 1 ; 3).
Calcule la longitud de la mediana relativa al lado BC.
a) 5 b) 7 c) 2 3
d) 13 e) 15
32. Si tres vértices consecutivos de un paralelogramo son
A( 1 ; 1) , B(1 ; 5) y C(9 ; 7).
Halle la suma de coordenadas del cuarto vértice "D"
opuesto a B.
a) 5 b) 6 c) 9
d) 10 e) 12

33. Se traza un segmento desde A(1;1) hasta B(3;5). ¿Hasta
qué punto "C" será necesario prolongarlo para que
AC BC ?
6 5
(Señale la suma de coordenadas de "C")
a) 35 b) 38 c) 42
d) 23 e) 27
34. En un triángulo ABC se sabe que A(3 ; 5) y el baricentro
es G(1 ; 3). Hallar la suma de coordenadas del punto
medio de BC.
a) 3 b) 5 c) 7
d) 5 e) 7
35. Del esquema mostrado, determine las coordenadas del
punto M.
Si: ABCD es un paralelogramo.
a)
c)
B
11
; 8
2
9
;
2
5
e) ( 5 ; 7)
A( 8 ; 5)
M
y
N
b) ( 6 ; 5)
d) ( 6 ; 4)
C(4 ; 9)
D(6 ; 1)
36. Se tiene el triángulo formado por los vértices A(1;9),
B(6 ; 8) y C( 2 ; 4), calcule la superficie del triángulo.
a) 35
2 b) 28
2
c) 14
2
d) 24
2
e) 40
2
37. Si A(-1;3) , B(3;1) y C(2;4), calcule el Seno del ángulo
CAB.
3
a)
10
2
d)
5
10
b)
10
2
e)
2
5
c)
5
x
38. Del gráfico, halle :
a)
( 3 ; 1)
2
10 b)
2 2
d) 11, 5 e) 12
2 1
S S .
(5 ; 8)
S2
2
10, 5 c)
S1
6
(6 ; 2)
2
(10 ; 1)
39. Los puntos P(-4;0); Q ( 5 ; 3 3)
, R(x;0) son los vértices
de un triángulo rectángulo recto en Q, la suma de los
valores que indican el perímetro y el área del triángulo
es:
a) 18 3 24 b) 18 18 3
c) 18 24 3 d) 12 12 3
e) 12 6 6
40. La base mayor de un trapecio isósceles une los puntos
(-2;8) y (-2;-4). Uno de los términos de la base menor
tiene por coordenadas (3;-2).
La distancia o longitud de la base menor es:
a) 8 b) 6 c) 9
d) 12 e) 10
41. Un cuadrilátero tiene sus vértices en los puntos
coordenados :
A(0;0) , B(2;2) , C(7;2) y D(5;0)
PROPOSICIÓN 1:
Si sólo los valores de las abscisas se multiplican por 2
entonces este cuadrilátero es semejante al original.
PROPOSICIÓN 2:
Si los valores de las abscisas y ordenadas se multiplican
por un mismo número, entonces este cuadrilátero es
semejante al original.
PROPOSICIÓN 3:
Si los valores de las abscisas se multiplican por 2 y las
ordenadas por 3 entonces el área de este nuevo
cuadrilátero es 5 veces mayor que el original.
a) FVV b) FFV c) VFF
d) FFF e) VVF

42. Los vértices de un cuadrado son A(0 ; -3); B(
b ; b ) ,
1 2
C(3;4), D(
d ; d ) .
1 2
Calcular el área del rectángulo cuyos vértices son los
puntos B, P, D, Q donde P(
d ; b )
1 2
y Q(
b ; d ) .
1 2
a) 58 b) 29 c) 25
d) 21 e) 19,5
43. En la figura mostrada las coordenadas del punto R son
( 6
3 ; 8)
.
Hallar la distancia del baricentro de la región triangular
MON al punto R.
y
M
R
30º
O N
a) 2 21 b) 21 c) 4 21
d) 21 e) 2 42
44. Si A(-3;4), B(4;5), C(1;-4) son los vértices de un
triángulo. Calcular las coordenadas del circuncentro del
triángulo.
a) (1 ; 1) b) (1 ; -1) c) (2 ; -1)
d) (-3 ; -1) e) (-1 ; -1)
45. Sean los puntos del plano cartesiano:
A(3 ; 10), B(13 ; 2) , C(0 ; a) y D(b ; 0).
Hallar los valores de a y b de tal forma que la suma de
las longitudes de los segmentos AC, CD y DB sea lo
menor posible y dar como respuesta el valor de 12ab.
a) 961 b) 828 c) 780
d) 1020 e) 605
46. Sean los puntos del plano cartesiano A(1;2) B(10;0) y
C(8;4). Desde el punto C se baja la perpendicular CP
al segmento AB, entonces las coordenadas de P son :
a)
b)
c)
1
1
1
9
9
9
6
7
59
85
59
85
; 2 - 2
; 2
2
; 2 - 2
6
7
59
85
59
85
x
d)
e)
1
1
9
9
6
13
6
13
; 2
; 2
2
2
6
13
6
13
47. Las coordenadas de los vértices A y B de un rectángulo
ABCD son (12 ; 3) y (4 ; 9), respectivamente. Si el área
de la región rectangular es 2
80 u , determinar la suma
de las abscisas de los vértices C y D.
a) 25 b)
d)
127
5
e)
126
5
128
5
c) 26
48. Si los puntos (1 ; 6) y (5 ; 2) son los vértices opuestos
de un cuadrado, entonces el área del cuadrado es:
a) No se puede determinar.
b) 50 c) 4
d) 16 e) 8
49. Los puntos A(-2 ; 2), B(0 ; 4), C(
C ; C ) son los vértices
1 2
de un triángulo equilátero.
Si C está en el segundo cuadrante, entonces
3(
C
1
C ) vale:
2
a) - 9 b) - 8 c) - 6
d) - 5
e) 2 3
50. Dados los puntos A(-2;-3) , B(2;1), C(4;-9) y M punto
medio de BC , la distancia de M al segmento AC es:
a) 2 b) 2 2
d) 4 2
e) 6
c) 4
51. En la gráfica, si AC = 5, la suma de las coordenadas de
C es:
y
O
A(1;2)
a) 4 b) 10 c) 8
d) 6 e) 9
C(x;y)
B(4;2)
x

52. Los extremos de la base de un triángulo son los puntos
A(0 ; 0) y B(3 ; 0).
Determinar la ordenada del vértice opuesto C
1
2
; y
de tal manera que la medida del ángulo CAB es igual al
doble de la medida del ángulo CBA.
a) 15 b)
d)
15
6
e)
15
2
15
8
c)
15
4
53. A(a ; b), B(a ; -b), C(-a ; -b), D(-a ; b) son los vértices de
un rectángulo. Si: P(x;y) cumple que DP 6 ,
CP 7 y BP 5 , entonces el valor de AP es:
a) 5 b) 2 3
d) 4 e) 3 2
c) 3
54. En el gráfico: BD = 3AD y EC = 2BE.
Calcule:
y
W
h1 A(1;1)
h h
2 3
h
1
D
B(5;5)
h 3
a) 1 b) 2 c) 3
2
d) 4 e)
3
55. Del gráfico, calcule "x" si " " es máximo.
y
(3;3)
(1;1)
E
P(x;0)
a) 2 b) 2 2 c) 3
d) 2 3 e) 6
h 2
C(8;2)
x
x
56. A partir del gráfico, calcule:
W
A(1;3)
Sen
2
Sen
2
2
Sen
B(3;9)
a) 1 b) 2 c) 3
2
d)
3
3
e)
2
C(5;7)
57. Del gráfico, halle la suma de coordenadas del punto
"P". Si :
BD
3
DC
5
A(2;0)
B(3;9)
7S
D
a) 8
b) 10 c) 12
d) 16 e) 7
P
S
C(7;5)
58. De todos los puntos del plano cuya suma de distancia
a los puntos A(1;5) y B(7;5) es igual a 10. Señale la
suma de coordenadas de aquel punto de ordenada
máxima.
a) 10 b) 11 c) 12
d) 13 e) 14
59. Señale las coordenadas del vértice C, del triángulo ABC,
si las coordenadas de los vértices del triángulo formado
al unir los puntos medios de sus lados son:
(
A M
1 ; 0)
, B ( 2 ; 3)
M y C ( 6 ; 7)
M
y
A
C
B M
A M
C M
a) (-9 ; -4) b) (-7 ; - 2) c) (-10 ; -5)
d) (-8 ; -5) e) (-6 ; -7)
B
x

60. Si ABCD es un paralelogramo, halle: 1 2
S S
y
C(x;y)
D(-3;2)
S1
A(-5;-5)
S2
B(2;-1)
x
a) 41
4
2 b) 41
2
2 c) 21
2
2
d) 21
4
2 e) 41
2

Claves
Claves
c
c
c
d
e
b
c
c
d
c
c
b
b
b
d
e
a
d
a
b
c
d
b
c
e
d
a
d
b
b
d
d
b
c
a
c
e
c
c
a
a
d
a
a
a
c
e
d
e
b
b
b
b
c
e
a
b
d
a
b
01.
02.
03.
04.
05.
06.
07.
08.
09.
10.
11.
12.
13.
14.
15.
16.
17.
18.
19.
20.
21.
22.
23.
24.
25.
26.
27.
28.
29.
30.
31.
32.
33.
34.
35.
36.
37.
38.
39.
40.
41.
42.
43.
44.
45.
46.
47.
48.
49.
50.
51.
52.
53.
54.
55.
56.
57.
58.
59.
60.

Capítulo
5
Definiciones Previas:
I. ÁNGULO EN POSICIÓN NORMAL
RAZONES TRIGONOMÉTRICAS DE UN
ÁNGULO EN POSICIÓN NORMAL
Llamado también en posición canónica o stándar. Es aquél ángulo trigonométrico cuyo vértice coincide con el origen
del sistema cartesiano y su lado inicial coincide con el eje "x" positivo.
Cuando un ángulo, está en posición normal, el lado final puede estar en uno de los cuadrantes, en cuyo caso se dice
que éste pertenece a tal cuadrante.
Lado Final
Vértice
* : es un ángulo en posición normal
* IIC ; 0
y
(+)
x
Lado Inicial
Definición de las Razones Trigonométricas:
Vértice
Lado Final
y
Lado Inicial
x
(-)
*
: es un ángulo en posición normal
* IIIC
; 0
Para determinar el valor de las R.T. de un ángulo en posición normal, tomaremos un punto
lado final.
P(
x ; y )
0 0
perteneciente a su
*
P( x ;y )
o o
x o
r
'
y
y o
x
Se define:
Sen
Cos
Tan
y
o
r
x
o
r
y
o
x
o
Cot
Sec
Csc
x
o
y
o
r
x
o
r
y
o
r x
2
y
2
*
o o
' : se denomina ángulo de referencia

Signo de las R.T. en los cuadrantes
Dependiendo del cuadrante al que
pertenezca un ángulo en posición
normal, sus R.T. pueden ser positivas
o negativas. Es así como se obtiene
el cuadro adjunto.
Razones Trigonométricas de Ángulos Cuadrantales
(+)
(+)
Seno
y
Cosecante
Tangente
y
Cotangente
(+)
(+)
Todas
son
positivas
Coseno
y
Secante
radianes (grados) Sen Cos Tan Cot Sec Csc
0 2 0 0 1 0 N. D. 1 N. D.
2
3
2
Nota: N.D. no definido
90º 1 0 N. D. 0 N. D. 1
180º 0 - 1 0 N. D. - 1 N. D.
270º - 1 0 N. D. 0 N. D. - 1
Ángulos Coterminales:
Son aquellos ángulos trigonométricos que poseen el mismo vértice, el mismo lado inicial y final.
Ejemplo:
i)
Lado
inicial
ii)
Lado
final
Se tiene que :
* y : son coterminales
* y : son coterminales (están en P. N.)
Propiedades:
Si y son coterminales se cumple que:
Vértice
I. II.
P( x ; x )
o o
- = 360ºn ; n Z R.T. ( ) = R.T.( )
y
x

01. Del siguiente gráfico, calcular: E 10Sen
12Cot
a) 0 b) 1 c) 2
d) 3 e) 4
y
(1;-3)
02. Por el punto P(
2;
5)
pasa el lado final de un ángulo
en posición normal cuya medida es " ". Calcular:
Cos .
03. Si:
a) -1/2 b) -2/3 c) -3/4
d) -4/3 e) -3/2
Sen
2
y IIIC. Calcular:
3
E
5(
Tan
a) -1 b) -2 c) -3
d) 2 e) 3
Sec
04. Indicar el signo de cada expresión:
I. Sen200ºTan240º
II. Cos120ºTan100º
III. Sen150ºCos340º
a) +, +, + b) , , c) , +, +
d) +, , e) +, , +
05. ¿A qué cuadrante pertenece " ", si: Tan 0
Cos
0 .
a) IC b) II c) IIIC
d) IV e) IC y IIC
06. De la figura, calcular: " Tan "
(1-x;2x)
17
a) 1 b) -2 c) -3
d) -4 e) -5
y
x
)
EJERCICIOS PROPUESTOS
x
y
07. Calcular:
E
( a
b)
2
Sec360º
( a b)
2
Cos180
2abCsc
270
a) 1 b) 2 c) 3
d) -3 e) -2
08. Si: x IVC y | Cscx | 4Sen
0
6
Calcular: E = Senx + 3 Cosx
a) 1 b) 1/2 c) 1/3
d) 2/3 e) 3/2
09. Si: Cos 0,
3 y IIC
Calcular:
2
E Tan Sec
a) 1 b) 2 c) 3
d) 4 e) 5
10. Si: f(x)=2Sen2x+3Cos3x+4Tan4x.
Calcular:
f(
)
2
a) 0 b) 1 c) 2
d) -1 e) -2
11.Una raíz de la ecuación: x 2x
3 0
2
11.Una raíz de la ecuación:
es un valor de
"Tan ", si: IIIC . Calcular: E 10(
Sen Cos )
a) -1 b) -2 c) -3
d) -4 e) -5
12. Si: f(x)=Senx+Cos2x+Tan4x.
Calcular:
f(
)
2
a) 0 b) 1 c) 2
d) -1 e) -2
13. Si: y son medidas de ángulos coterminales y se
cumple que: Tan

14. Calcular: E
mostrada:
25Sen
Tan , a partir de la figura
y
(-4;-8)
a) 1 b) 3 c) 5
d) 7 e) 9
(24;7)
15. Por el punto P( 2;
7 ) pasa por el final de un ángulo
en posición normal cuya medida es " ". Calcular:
7 Csc
.
a) 1 b) 2 c) 3
d) -3 e) -2
16. Calcular: E Senx Cosx 1
a) 0 b) 1 c) 2
d) 2 e) 2 2
17. Si: IV , determine el signo de: E
a) + b) - c) + ó -
d) - y + e) Todas son correctas
x
Tan ( 1 Cos )
Sen Cos
18. Con ayuda del gráfico mostrado, calcular:
E
3Cos(
6
)
3Sen(
Sen(
a) 1/2 b) 2/3 c) 3/4
d) 4/3 e) 3/2
19. De la figura, calcule: "Tan "
2
)
)
37º
y
x
a) -3/7 b) -4/7 c) -5/7
d) -6/7 e) -7/4
20. Del gráfico, calcule: " Tan
y
" .
a) 1/2 b) 2/3 c) 3/4
d) 4/3 e) 3/2
21. De acuerdo al gráfico calcular:
K
(-24;7)
5Cos
(-4;-3)
y
x
(2;-3)
Cos
a) 2 b) 3 c) 4
d) 2 e) 4
22. Si el punto Q(8; 5) pertenece al lado final de un ángulo
canónino " ".
Calcular:
R
Csc
Cot
a) 0,4 b) 0,4 c) 0,6
d) 0,6 e) 0,3
23. Simplificar:
L
( a
2 3
b)
Sen
2
aSen
3
2
a) 2a b) 2a c) 4a
d) 4a e) 4b
24. Señale los signos de:
R
( a
x
bCos
2
2
2 5
b)
Cos
M
Sen140º
Cos140º
y
Tan300º
Tan260º
Tan160º
Cos217º
Tan116º
Cos248º
Sen348º
a) ( ) No se puede precisar.
b) (+) ; (+)
c) (+) ; ( )
d) ( ) ; ( )
e) ( ) ; (+)

25. Señale Verdadero (V) o Falso (F) según corresponda
en:
I. Si: Sen 0 Cos 0 , entonces IV .
II. Si: Tan 0 Sec 0 , entonces IIIC .
III. Si: Csc 0 Cot 0 , entonces IIC .
a) VVF b) VVV c) VFV
d) FFV e) FVV
26. Sabiendo que:
Sen
Tan
0
Sec
0
¿A qué cuadrante pertenece el ángulo canónico ?
a) IC b) IIC c) IIIC
d) IVC e) No se puede precisar.
27. Señale el cuadrante al que pertenece " " si:
Cos
Tan
a) IC b) IIC c) IIIC
d) IVC e) No se puede precisar
28. Señale Verdadero (V) o Falso, según corresponda en:
I. Si: 90 º ; 180º , entonces IIC .
II. Si: IIC , entonces 90 º ; 180º .
a)
d)
1
13
5 13
13
b)
e)
3
13
13
13
c)
5
13
30. Si el lado final de un ángulo canónico "
puntos P(m+n; n) y Q(n;m n),
" pasa por los
Calcular: K
2
Cot
2
Tan
a) 2 b) 4 c) 6
d) 8 e) 12
31. Sabiendo que " " es un ángulo positivo menor que
una vuelta perteneciente al IIIC señale el signo de:
Q
Sen
2
Cos
2
3
Tan
3
5
a) (+) b) ( ) c) (+) o ( )
d) (+) y ( ) e) No se puede precisar.
32. Del gráfico, calcular :
E
3Tan
53º
a) 0 b) 1 c) 1
d) 2 e) 2
1
y
33. Tomando 5 2,
236 y sabiendo que:
Ctgx = - 0,5 y que x IVC .
¿Cuál es el valor de Cscx?
a) 2,236 b) 2,236 c) 0,4472
d) 1,118 e) 1,118
34. Los cuadrantes en los que el Coseno y Tangente tienen
el mismo signo son:
a) 1º y 2º b) 1º y 3º c) 2º y 3º
d) 2º y 4º e) 1º y 4º
III. Si: IIIC , es positivo y menor que una vuelta, 35. Se tienen dos ángulos coterminales tales que el mayor
entonces 180 º ; 270º .
es al menor como 23 es a 2. Su suma está comprendida
entre 2820º y 3100º.
a) VVF b) VFV c) VFF
¿Cuál es la medida del mayor?
d) FVV e) VVV
a) 2540º b) 2760º c) 2820º
d) 2420º e) 3000º
29. Sabiendo que: Tan
2
3
36. Siendo:
IIC
Calcular: Q Sen Cos
4
Sen
5
1
4
1
28
1
70
1
130
Cos
Calcular:
Cos
K
2Sen
a) 1 b) 1 c) 2
d) 2 e) 3
3Cos
37. El valor numérico de la expresión:
Sen180º+2Cos180º+3Sen270º+4Cos270º- 5Sec180º-6Csc270º
es:
a) 4 b) 12 c) 6
d) 16 e) 8
x

38. Indicar los signos de las siguientes expresiones en el
orden F. G. H.
F
G
H
39. Si:
Tan
2
Sec285º
138º
Sen210º
3
Csc 215º
Ctg338º
3
Sen
3
260º
Ctg
2
115º
Cos116º
2
Csc195º
Tan 336º
Sen195º
Ctg340º
Csc128º
Tg135º
Sec298º
a) , + , b) , , + c) , ,
d) + , , e) + , + , +
f(
Calcular:
a) 2 b)
d) 3 2 3 e)
)
Cos(
3
f
)
3
1
3
f
3
3
2
Sen ( 2 )
3
3
2 c) 5
2
2
3
3
2
1
Cos2
40. Determinar el signo de S en cada uno de los cuadrantes
(I, II, III, IV).
S = Ctgx + Senx - Cscx
I II III I V
a) + + + +
b) + + +
c) + +
d) + +
e) + +
41. Determinar el signo de:
3 5 4
Sen QSec QCtg Q
a) ; si Q pertenece al IC.
b) + ; si Q pertenece al IIC.
c) + ; si Q pertenece al IIIC.
d) + ; si Q pertenece al IVC.
e) ; si Q pertenece al IIC.
2 2
42. Dado:
p q
Cosx ; p > q > 0
p
2
q
2
Calcular Tgx, con x en el segundo cuadrante.
2pq
a) 2
q
2
p
2 pq
c) 2
q
2
p
2pq
b) 2
q
2
p
2 pq
d) 2
q
2
p
q
2
p
2
e) 2 2
q p
43. Sabiendo que: CosQ
270º < Q < 360º
1
4
Calcular el valor de la expresión:
SecQ CscQ
1 CtgQ
a) 0,25 b) 0,50 c) 2,50
d) 4,00 e) 4,50
44. Si es un ángulo del tercer cuadrante, tal que:
1
2
Ctg
Calcular:
a) 8 63
3
d)
8
3 63
3
8
( 8Sec
b)
e)
3
)
8
63
3
8
63 63
6
45. Si el ángulo x es positivo, pertenece al cuarto cuadrante
y es tal que: 0 x 2 . Entonces, hallar el signo de
las siguientes expresiones trigonométricas.
I.
II.
III.
Sen
x
2
Tan
x
4
Co sec
Cot
x
3
Sec
Cos
x
5
Sen
x
3
Sec
Tan
3x
4
3x
4
x
4
2x
3
c)
8 3
a) (+) (+) (+) b) ( ) ( ) ( )
c) (+) (+) ( ) d) ( ) ( ) ( )
e) ( ) ( ) (+)
46. Hallar el signo de las expresiones trigonométricas, en
el orden dado:
63
Sen
52
Cos
25
; Sen
32
Cot
22
;
3 3 5 3
Sen
205
3
Cot
73
10
a) (+) (+) ( ) b) ( ) (+) ( )
c) ( ) (+) (+) d) ( ) ( ) (+)
e) (+) ( ) (+)

47. Si es un ángulo en el primero cuadrante y
Sen 0,
25 .
¿Cuál es el valor de Csc Ctg
2
?
21
a) 15 b)
19
19
d)
21
e) 19
19
c)
15
48. Si Tg 1,
5 , siendo un ángulo en el III cuadrante,
el valor de la expresión:
a)
d)
1
6
5
6
1
M ( Sec Csc ) es :
13
b)
e)
1
6
1
6
1
c)
6
49. Calcular el Coseno del ángulo del segundo
cuadrante, tal que
4
a)
5
d)
50. Si
4
5
3
b)
5
e)
Sen
3
.
5
1
3
Tan
1
y está en el segundo cuadrante.
3
Hallar : K
a) 10 b)
d)
2
10
5
c)
3(
Cos 5Sen
)
2Ctg
e)
2
3
10
10
c)
10
10
2 10
5
51. En la figura adjunta, hallar:
141
a)
35
39
d)
7
V
5Sen
29
b)
7
1
e)
4
15Cos
y
24
Tan
- 7 0 x
99
c)
35
52. Indicar la alternativa correcta para el signo de las
siguientes expresiones:
I. Sen(361º) Cos(455º)
II.
III.
Sen
Tan
3
4
5
4
Cos
3
4
Sec(
315º
)
a) + ; ; + b) + ; + ; c) ; ; +
d) + ; ; e) + ; + ; +
53. Sea un ángulo del tercer cuadrante.
Indicar la alternativa correcta al simplificar:
E
1
1
2
Sen
a) 2
2
Sen b) 2
Sen
c) 1
2
Cos d)
2
Sen
e) 2
Cos
Cos
54. Si: Senx = 0,6, ¿cuál es el valor de Cosx, sabiendo que
x es un ángulo del segundo cuadrante?
a) Cosx = 0,8 b) Cosx = 0,6
c) Cosx = 0,7 d) Cosx = 0,9
e) Cosx = 0,8
55. Si " " y " " son ángulos cuadrantales, positivos y
menores que una vuelta, tales
que:
Calcule:
Cot Cos
K
Cos
Sen
2
Sen
2
Cos
a) 2 2 b) 2 1 c) 2 1
d) 2 2 e) 1
56. Si y son ángulos positivos, que no son agudos;
Sean:
Cos 0 ; Tan 0 ; ( 360º
)
a = Sen(
)
b = Sen2
c = Sen2
Entonces, son positivas.
a) a y b. b) a y c. c) a , b y c.
d) a. e) b y c.

57. Si: Tanx
a
b
2
3
Calcular el valor de:
E
a
bSenx
a)
c)
e)
1
a 3
1
b 3
2
a
b
2
3
a
b
3
1
b 3
1
a 3
2
b
a
2
3
b
a
3
3
1
2
1
3
b)
d)
a
b
b
aCosx
b
a
2
a 3
2
b 3
2
b 3
2
a 3
; x
58. Hallar todos los valores que puede tomar el ángulo
del primer cuadrante, cuyo ángulo doble está en el
segundo cuadrante, su ángulo triple está en el tercer
cuadrante y su cuádruple en el cuarto cuadrante; pero
inferior a 2
a)
4
2
c)
5
12 2
e) Faltan datos
b)
d)
3
3
8
2
2
3
2
IC
59. Si: IIC y
3 4 2
Sen
Calcular: Tg Sen
a)
c)
e)
11
12
13
12
11
12
143
143
143
b)
d)
13
12
9
12
( Sen
143
143
Cos
)
60. Se tiene dos ángulos que se diferencian en un múltiplo
de 360º. Se sabe que el cuádruple del menor es a la
suma del ángulo menor más el triple del mayor de los
ángulos, como 4 es a 5. Hallar el menor de los ángulos,
si se sabe que está comprendido entre 1080º y 3240º.
a) 1280º b) 2160º c) 3200º
d) 3210º e) 3230º

Claves
Claves
b
b
a
c
d
d
e
a
e
a
d
b
b
e
d
a
a
e
b
b
c
c
e
d
a
b
d
b
b
c
b
c
e
a
b
d
c
a
c
c
c
b
d
e
c
b
e
a
d
b
d
e
d
e
a
e
d
d
c
b
01.
02.
03.
04.
05.
06.
07.
08.
09.
10.
11.
12.
13.
14.
15.
16.
17.
18.
19.
20.
21.
22.
23.
24.
25.
26.
27.
28.
29.
30.
31.
32.
33.
34.
35.
36.
37.
38.
39.
40.
41.
42.
43.
44.
45.
46.
47.
48.
49.
50.
51.
52.
53.
54.
55.
56.
57.
58.
59.
60.

Capítulo
6
REDUCCIÓN AL PRIMER CUADRANTE
OBJETIVO: El objetivo del presente capítulo es:
* Calcular las razones trigonométricas de un ángulo que no es agudo, en función de otro que sí lo sea; reconociendo
previamente el caso en que nos ubicamos y el criterio a utilizar.
* Simplificar correctamente expresiones del tipo: R.
T.
n
; n Z
2
* Reconocer y aplicar correctamente las propiedades de ángulos cuya suma de medidas es 180º ó 360º
CASOS
I. Ángulos cuyas medidas están en : En este caso, el ángulo original " " se descompone como la
suma o resta de un ángulo cuadrantal (90º ; 180º ; 270º ó 360º) con un ángulo que sea agudo; para luego aplicar :
RT
( )
R
R
180
360
90
220
Donde el signo ( ) que deberá anteponerse al resultado dependerá del cuadrante al que pertenezca el ángulo original "
"
Por ejemplo; calculemos:
*
*
*
*
*
*
*
*
Sen120º
( )
Cos120º
( )
Tan 240º
( )
Csc330º
( )
Sen170º
Cos200º
Tan260º
Sen320º
Sen(
90º
Cos(
180º
Tan(
270º
Csc(
360º
Sen(
Cos(
Tan(
Sen(
30)
60º
)
30º
)
30º
)
)
Cos30º
)
)
)
Cos60º
Cot 30º
Csc 30º
3
2
2
3
1
2
R.
T.(
Co
)
R.
T.(
II. Ángulo cuya medida es mayor que 360º: En este caso, se procede de la siguiente manera:
R.T. ( ) = R.T. ( ) ; donde 360º
q
)
Residuo

Por ejemplo, calculemos:
*
Sen 2580º
Sen60º
3
2
* Tan 3285º = Tan45º = 1
2580º 360º
3285º 360º
2520º 7
3240º 9
60º
45º
* Sec1200º = Sec120º = Sec(90º + 30º) = Csc30º = 2
1200º 360º
1080º 3
120º
* Sen 3180º =
( )
Si el ángulo estuviese expresado en radianes, se procede de la siguiente manera:
*
Sen133
2
133 4
132 33
1
Sen
1
2
1
*
Cos127
3
127 6
126 21
1
Es decir, si fuese: R.
T.
a
b
; a 2b
Se divide: a 2b
q
r este residuo reemplaza al numerador "a"
*
Tan1315
4
1315 8
51 164
35
3
Tan
3
4
*
Sen 1345
3
1345
Cos
1
3
III. Ángulos de medida negativa: Se procede de la siguiente manera:
Por ejemplo, calculemos:
*
2
Sen ( 45º
) Sen45º
*
2
* Tan ( 120º
) Tan 120º
* Cos (- 200º) =
( )
IV. Ángulos relacionados:
1.
2.
Si : x
y
180º
Senx
Cosx
Tanx
Sen(-x) = -Senx Csc(-x) = -Cscx
Cos(-x) = Cosx Sec(-x) = Secx
Tan(-x) = - Tanx Cot(-x) = - Cotx
Tan ( 90º
Seny
Cosy
Tany
30º
)
(
Cos(
Cot30º
)
60º
)
3
1
2
Cos60º
1
2

Si : x
y
360º
Por ejemplo, calculemos:
Senx
Cosx
Tanx
En esta expresión note que:
7
2
7
3
7
6
7
5
7
4
7
Luego:
Cos
7
Cos
2
7
Cos
3
7
C
Cos
6
7
Seny
Cosy
Tany
Cos
5
7
Cos
4
7
C
Reduciendo, quedaría C = 0
Cos
7
Cos
6
7
Cos
2
7
Cos
5
7
Cos
3
7
Cos
4
7
Cos
4
7
Cos
4
7
Cos
5
7
Cos
5
7
Cos
6
7
Cos
6
7

01. Señale el valor de: Sen120º
3
a) 1/2 b) -1/2 c)
2
d)
3
2
02. Hallar: Cos330º
2
e)
2
3
a) 1/2 b) -1/2 c)
2
d)
3
2
2
e)
2
03. Calcule: E = Tg150º.Sen315º
6
a)
4
d)
6
6
b)
e)
6
4
2
4
04. Hallar el valor de: Sen1680º
6
c)
6
a) 1 b) -1 c) 1/2
d) -1/2 e)
3
2
05. Determinar el valor de: Cos1200º
a) 1 b) 0 c) 1/2
3
d) -1/2 e)
2
06. Hallar: E Cos(
60º
) Tg(
45º
)
a) 1/2 b) -1/2 c) 0
d) 1 e) 2
07. Hallar: E = Sen(-30º)+Tg(-53º)
a) 11/6 b) 6/11 c) -11/6
d) 0 e) 1
08. Señale el equivalente de: Cos(180º+x)
a) Cosx b) -Cosx c) Senx
d) -Senx e) -Secx
09. Determinar el equivalente de: Sen(360º-x)
a) -Senx b) Senx c) Cosx
d) -Cosx e) Cscx
EJERCICIOS PROPUESTOS
10. Determina el equivalente de:
a) 1 b) -1 c) 0
d) 1/2 e) -1/2
11. Hallar el valor de: Cos1741
a) 1 b) -1 c) 0
d) 1/2 e) -1/2
12. Hallar:
Tg17.
3
a) 1 b) -1 c) 3
d) 3 e)
3
3
13. Del gráfico, calcule: Tg
A
45º
M
a) 1 b) 2 c) -1
d) -2 e) 3/4
14. Del gráfico, hallar: Tg
A
D
37º
a) 3/4 b) -3/4 c) 3/7
d) -3/7 e) -4/7
15. Hallar el equivalente de:
M
Sen(
x 180º
)
Cos(
x 90º
)
a) 1 b) -1 c) Tgx
d) Ctgx e) -Tgx
Sen ] 32 ].
C
B
C
B
2

16. Si: Sen(-x) + 2Cos(-x) = 2Senx ;
x es agudo
Calcular: M = Sec(-x) + Csc(-x)
5
a)
2
d)
13
6
17. Reducir:
A
b)
e)
5
2
5
5
c)
13
6
Sen(
90º
x)
Tan(
180º
x)
Csc(
270º
x)
Cos(
180º
x)
Sec(
360º
x)
Cot(
180º
x)
a) 1 b) 1 c) Tan x
2
d) Cot x
2
18. Simplificar:
a)
d)
C
2
Tan b)
2
Ctg e) 1
19. Simplificar:
e) Tan x
2
C
Sen(
) Cot(
2
Tan(
2
2
Tan c) Ctg
Sen(
Tan(
x)
Tan
x)
Cos
3
2
3
2
a) Cotx b) Cot x
2 c) Cot x
2
d) - Cotx e) Cot x
3
20. Si : 0
Evaluar:
F
Sec
Sen
A
2
2
A
2
A
Cos(
Ctg(
2
A)
A)
Tan
Csc(
a) 2 SenA b) 2SenA c) 2CscA
d) 2CscA e) 2SecA
21. Calcular:
M
2Sec120º
1
4Tan315º
1
a) 1 b) 2 c) 3
d) 4 e) 2
3
2
) Sec
x
x
)
A)
A
3Tan240º
3
2
22. Calcular:
6
a)
3
d)
2 6
3
23. Calcular:
1
a)
2
1
d)
4
U
C
b)
e)
Sen135º
Sen240º
Tan150º
Cos 210º
Cos300º
6
3
2
3
c)
2 6
3
( 2Sec3000º
1)(
2Sen3383º
2Cos4920º
1
b)
e)
1
2
3
4
1
c)
4
24. Marque Ud. la afirmación correcta:
a) Sen ( 750º) = 0,5
b) Cos(
1110º
) 0,
5 3
c)
Tan(
1830º
)
3
3
d) Ctg(
3270º
) 3
e) + Sen2534º = Cos14º
25.
Hallar el valor numérico de:
31
a)
12
d)
33
20
F
1)
2
Sen 225º
2
Tan 330º
2
Sen 780º
2
Tan 780º
2
Tan 330º
2
Ctg 225º
33
b)
20
e)
31
12
26. Simplificar las expresiones:
a
b
Cos(
)
Cos(
180º
Sen(
90º
)
Cos(
)
)
1
c)
44
Sen(
360º
Sen(
)
Cos(
90º
Sen
a) a = 0 y b = 2
b) a = 1 y b = 2
c) a = 2 y b = 2
d) a = 0 y b = 0
e) a = 1 y b = 2
27. Si: x + y = 180º
Calcule el valor de:
y + z = 270º
J
Senx
Seny
Tany
Ctgz
)
)

a) 1 b) 0 c) - 3
d) 2 e) - 5
28. Si: Tanx + Ctgy = 2 ;
Hallar: Ctgx
x y
a) 2 1 b) 1 2 c)
d)
1 2 e) 2 1
2
29. Simplificar la expresión:
E
Sen(
180º
Cos(
540º
Sabiendo que : Sec 2
2
Entonces E es igual a :
2 1
2
) Cos(
90º
) Tan(
2160º
) Sen(
450º
) Tan(
360º
a) 2 b) 1 c) 1
d) 2 e) 0
30. El valor de la expresión:
E
Cuando :
Sen
Ctg(
2
3
2
6 es:
)
Cos(
Sec(
a) 1 b) 1 c) 0
d) 2 e) 2
)
)
Csc
Tan
31. Calcular el valor de:
Cos10º+Cos30º+Cos50º+.... +Cos170º
1
a)
2
3
d) 1 e)
4
T
32. Calcular:
3
b) 0 c)
2
Cos
30
Cos
2
Cos
3
30 30
20 términos
a) 0 b) 1 c) - 1
d) 2 e) - 2
33. El valor de la siguiente expresión:
Es igual a:
Sen
Cos
7
12
12
a) 0 b) 1 c) - 1
d) 2 e) - 2
Sen
12
Cos
7
12
2
...
6
)
)
Cos
29
30
34. Simplificar:
K
Tan
5
2
Cos(
5
Sen
7
2
) Csc(
7
a) 0 b) 1 c) 1
d) 2 e) 2
Sec
9
2
) Ctg(
9
35. En un triángulo ABC se cumple:
Sen (B + C) = CosC
Dicho triángulo es :
a) Escaleno b) Rectángulo
c) Isósceles d) Acutángulo
e) Equilátero
36. En un triángulo ABC, se cumple que:
Cos (A + B) = CosC
Entonces el valor de A + B es :
a) 4
d) 6
37. Calcular:
b) 3
e) 2
2
Cos A
2
c)
3
2
Sen B
Si se sabe que A y B son ángulos suplementarios.
a) 1
b)
1
d)
2
e) 1
1
2
c) 0
38. Si A y B son ángulos complementarios, al simplificar:
E
Se obtiene:
Sen(
A
Cos(
2A
2B)
Tan(
2A
B)
Tan(
4A
3B)
3B)
a) 3 b) 2 c) 2
d) 1 e) 1
39. En un triángulo ABC, cuales de las siguientes
proposiciones se cumplen:
I. SenA = Sen(B+C)
II. CosA = Cos(B+C)
III. SenB = -Sen(A+2B+C)
a) VVV b) VFV c) VFF
d) FVF e) FFF
40. Si : a b c
2
y Sen(a + b) = - Senc
¿Cuál de los siguientes resultados es verdadero?
a) Cos
2 4c
0
4
)

) Cos
4c
0
4
c) Cos
4c
0
2
d) Cos
4c
4
0
e) Cos(
4c
) 0
41. Calcule el valor de:
R Tan
37
4
Sec
175
4
a) 1 2 b) 2 2 c) 2
d) 2 e) 1 2
42. El valor que asume la expresión:
Cuando :
3 3 1
a)
13
c)
e)
3 3
3
Sen
2
Ctg
3
2
1
1 3
3
3
43. Sabiendo que:
Calcular:
mSen
3 es:
55
2
E
en términos de m.
b)
d)
Cos(
2
Sec(
)
1 3
13
3
3 3
3
Tan
Cos
1
)
77
2
Ctg
a) m
2 b)
2
m c) 2m
d) m e) m
44. Si : ( 1 k)
360º
1035º
, k Z
El valor de : Sen( 22,
5º
) será:
a)
c)
e)
3
2 b)
2
2
2
2
2 2
2
d)
2 3
2
2
2
2
Tan(
Csc
6
1
)
45. Qué relación existe entre a y b sabiendo que:
1
a)
2
1
d)
5
Tan
2a
3b
8
1
b)
3
1
e)
6
Ctg
6
1
c)
4
3a
4
2b
46. Si : SenA 2CosA = 0
Entonces el valor de:
E
Tan(
90º
Sen(
360º
A)
Sec(
180º
A)
Ctg(
270º
A)
A)
Csc(
180º
A)
Cos(
180º
A)
es:
5
a) 5 b) 5 c)
4
d)
5
4
e) 4
47. Hallar sabiendo que está en el tercer cuadrante, es
positivo, mayor que una vuelta y menor que dos vueltas
y:
75
a)
22
69
d)
22
73
b)
22
67
e)
22
Cos
Sen
11
71
c)
22
48. Si
es la medida de un ángulo agudo tal que:
Cos1996º
Calcular el valor de:
E
Csc15
a) 1 b) 1,5 c) 2
d) 2,5 e) 3
49. Sabiendo que:
M
N
Tan k
Csc
Calcular:
n
E
2
(-1)
n
2 2
M N
MN
;
;
k
n
Sen
Sen15
a) Tan Sen b) Tan Sen
c) Ctg Cos d) Ctg Cos
e) 1
Z
Z
0

50. Del gráfico.
Determinar:
1
a)
2
1
d)
2
K
51. Sabiendo que:
3Sen
6Cos
1
b)
3
1
e)
3
b
56
Tan(
n!
n 2
y
a b
3
a b
6
Donde: x IC
Calcule: W = Secx . Tanx
a
c)
Sena
Cosa
1
4
( 1)
n
x)
a) 2 3 b) 6 c) 3 2
d)
6
2 6 e)
6
52. Si : ABCD: cuadrado
Calcule: W Tan Tan
B
P
Senb
Cosb
2 Cotx
N
26º30'
A D
a) 2 b) 1 c) - 2
d) 1 e)
53. Del gráfico calcule:
Si: OA = OB
3
2
W
3Cot
55
C
M
x
A
O
a) 3 b) 4 c) 5
d) 6 e) 7
2
54. Del gráfico, hallar " Cot " en función de "
Si: AB = BC
".
C
y
a) Tan 1 b) Tan 1 c) Tan 1
d) Cot 1
e) Cot 1
A
55. Del gráfico, calcule:
Cos
r
a)
2R
d)
R
2r
b)
e)
r
2R
R
4r
R
4
c)
3
R
2r
56. En un triángulo ABC, se sabe que:
Calcular:
Sen(
A
W
1
1
B)
Cos2B
Sen4
A
2Cos(
B
a) 1 b) 2 c) 4
1
d) 1 e)
2
B
C)
Cos2C
Sen4B
r
B
SenC
x
Cos2A
Sen4C

57. ¿Cuál es la medida del mayor ángulo " " que cumple:
Sen
2
Cos
7
Si es mayor que 3 vueltas, pero menor que 4 vueltas.
97
a)
14
95
d)
14
101
b)
14
99
e)
14
58. De acuerdo al gráfico, calcule:
6
a)
12
d)
K
3
12
Sen
3
b)
12
e)
6
6
2
3
Tan
103
c)
14
y
c)
Cos
6
6
12
3
4
x
59. Reduzca:
5
a) Sec
9
G
2Tan(
57
4Sen(
82
b)
1
9
Sec
2
d) Csc e) Csc
9
)
)
3Cot
5Cos
c) 5Sec
57
2
79
2
60. Señale el signo de cada una de las expresiones:
R
H
G
Sen
20
7
1
Sen
25
8
Csc
44
9
Cos
36
7
Tan
12
11
Csc
27
7
Sec
9
5
Cot
21
8
a) (+) ; ( ) ; ( ) b) (+) ; ( ) ; (+)
c) (+) ; (+) ; (+) d) ( ) ; ( ) ; (+)
e) ( ) ; (+) ; (+)

Claves
Claves
c
c
c
e
d
b
e
b
a
a
b
d
d
d
b
d
e
d
b
d
d
b
a
c
c
c
d
e
b
d
b
a
a
c
b
e
e
e
b
b
e
a
e
d
c
a
a
b
a
a
b
d
b
e
b
b
d
c
c
b
01.
02.
03.
04.
05.
06.
07.
08.
09.
10.
11.
12.
13.
14.
15.
16.
17.
18.
19.
20.
21.
22.
23.
24.
25.
26.
27.
28.
29.
30.
31.
32.
33.
34.
35.
36.
37.
38.
39.
40.
41.
42.
43.
44.
45.
46.
47.
48.
49.
50.
51.
52.
53.
54.
55.
56.
57.
58.
59.
60.

DEFINICIÓN
Capítulo
7
CIRCUNFERENCIA TRIGONOMÉTRICA
CIRCUNFERENCIA TRIGONOMÉTRICA
Es aquella circunferencia canónica; es decir, con centro en el origen del sistema cartesiano; y con radio igual a la unidad del
sistema. En el gráfico adjunto, destacaremos los siguientes elementos:
A (1; 0) : origen de arcos
B (0; 1) : origen de complementos de arcos
A' (-1; 0) : origen de suplementos de arcos
B' (0; -1) : anónimo
El punto A(1;0) se denomina origen de arcos, ya que a partir de él se van a dibujar arcos orientados, con un signo
asociado, tan igual que en el caso de los ángulos trigonométricos; por ejemplo, en el gráfico:
: es un arco positivo
(sentido antihorario)
: es un arco negativo
(sentido horario)
Ahora bien, los puntos "M" y "N" se denominan extremos de arco; y dichos
arcos se denominarán arcos en posición nomal.
Si observamos en la siguiente C.T., notaremos que entre el arco y el ángulo central correspondiente, se cumple que
numéricamente son iguales; lo cual permitirá establecer una relación entre los números reales y el ángulo central
correspondiente, en radianes.
A'
C.T.
B
y
M
A' A
O
N
1
B
y
1
B'
M
O
rad
rad 1
B'
N
A
x
x
En el sector circular AOM; por longitud de un arco:
AOM = rad, esto es:
AOM (en rad) = AM (numéricamente)
Debido a esta relación, a cada arco le corresponde un ángulo central del mismo valor,
pero expresado en radianes.
x 2+ y 2=1
A'
B
R=1
O
y
B'
1
A
C.T.
x

Así mismo, podemos establecer: R.T. ( rad) = R.T. ( ) ; r
Con lo cual queda claro que las Razones Trigonométricas (R.T.) de un número real, son calculables al asociarles un ángulo
cuya medida está expresada en radianes, numéricamente igual considerado.
Es decir; por ejemplo:
Sen 2 = Sen 2 rad
Tan 3 = Tan 3 rad
Cos (-1) = Cos (-1 rad)
LÍNEAS TRIGONOMÉTRICAS
Son segmentos dirigidos (de medida positiva o negativa) que van a representar el valor numérico de una Razón Trigonométrica
de un cierto número (expresado graficamente como un arco); así como también permitirán analizar las variaciones de estas
R.T., así como su comportamiento.
Para comenzar con el análisis, se recomienda tener en cuenta las siguientes observaciones para la ubicación de arcos.
a) Para arcos representados por números enteros:
y
1,57=
2
3,14=
1
4,71= 3
2
O
O x
2 =6,28
C.T.
b) Para arcos con extremos en A, B, A' ó B' ( n z )
..., 3
A'
I. Línea Seno.-
y
B: ; ; ; ....
2 2 2
B':
A:
2n
A':
( 2n
B:
( 4n
B':
( 4n
3
1)
1)
2
3)
2
2
y
4 5
n
( 2n
: :
y
A; 0; 2 ; 4 ; ...
x
3
; ; ; ....
2 2 2
M
(+) 1 Sen
(+)
A' A
(-)
C.T.
N
Sen
(-)
B
B'
-1
x
1)
2
1
n
2
0
2 2
3
2
3
2
2
Sen 0 1 1 0 0 -1 -1 0
Esto es:
Sen
máximo :
mínimo :
1 Sen 1 ; r
1
1
6
x

II. Línea Coseno-
C.T.
A'
N
Cos
(-)
Observación:
: :
B
0
2
3
2 2
3
2
Cos 1 0 0 -1 -1 0 0 1
Esto es:
Cos
máximo:
mínimo :
1 Cos 1 ; r
Si consideramos el extremo de un arco cualquiera, notaremos que por ser un punto del plano cartesiano, tiene sus
y
propias componentes:
Por ejemplo, para "M" se nota que:
C.T. B
M
abscisa = Cos
N
Sen
Cos
ordenada = Sen
Luego:
A'
Sen
Cos
Sen
Cos
A
x
M = (Cos ; Sen )
De manera similar, las componentes de N son (Cos ; Sen )
III. Línea Tangente.-
A'
C.T.
-1
y
Cos
(+)
B'
(-) (+)
B
O
B'
1
y
M
N
M
A
x
T
P
Tan
A
Tan
(+)
(-)
x
:
1
1
0
2 2
3
2
3
2
2
Tan 0 0 0 0
Esto es:
B'
< Tan <
No hay máximo, ni mínimo
Consideración:
La L.T. tangente no está definida para arcos cuyo extremo esté en B ó B'; lo cual significa que la R.T. tangente no se define para
todo arco de la forma:
(
2n
1)
2
; n
Z
2

01. Poner el signo en:
I. Cos80º ( ) Cos 100º
II. Cos200º ( ) Cos 300º
III. Cosx ( ) Cos(x+20º)
x ; agudo
a) < ; < ; > b) > ; > ; <
c) > ; < ; > d) > ; < ; =
e) < ; > ; <
02. Poner el signo > ; < o = en:
I. Sen20º ( ) Sen80º
II. Cos10º ( ) Cos40º
III. Sen200º ( ) Sen300º
a) > ; > ; < b) < ; < ; <
c) > ; > ; > d) < ; > ; >
e) > ; < ; <
03. Indicar con "V" lo verdadero y con "F" lo falso:
I. Tg50º > Tg200º
II. Tg100º > Tg300º
III. Tg135º = Tg315º
a) VVV b) VFV c) FFV
d) FVF e) FFF
04. Determine el área de la región sombreada en la C.T.
y
B
A’ O A
B’
a) Sen b) -Cos c) Sen /2
d) -Cos e) -Cos /2
05. Determine el área de la región sombreada en la C.T.
y
a)
d)
Sen
2
Sen
2
B
A’ O A
b)
e)
Cos
2
B’
c)
Sen . Cos
2
Cos
2
EJERCICIOS PROPUESTOS
x
x
06. Determine el área de la región sombreada en la C.T.
a) Tg b)
d)
Tg
2
B
A’ O A
Tg
2
e) -Tg 2
y
B’
L
c) -Tg
07. Determine la variación de: E 4Sen
1
a) [ 3;
3]
b) [ 4;
4]
c) [ 3;
5]
d) [ 5;
3]
e) [ 2;
5]
08. Determine la variación de:
2
A 2Cos
3
a) [3,5] b) [1,5] c) [-3,5]
d) [-1,3] e) [-3,3]
09. Sabiendo que
IIC .
¿Cuál es la variación de :
L
3Sen
1?
a) 0 ; 2 b) 1; 2 c) 0 ; 3
d) 1; 1 e) 4 ; 2
10. Sabiendo que IIIC ; sabiendo la variación de:
L
2Cos
a) 1 ; 3 b) 1; 3 c) 1;
1
d) 0 ; 3 e) 2 ; 2
11. Calcular el producto del máximo y mínimo valor de:
f(
, , )
2
2Sen
3|
Cos | Sen
Siendo , y independientes entre sí.
a) 0 b) 4 c) 8
d) 8 e) 12
1
x

12. Hallar el área de la región sombreada en la C.T.
y
a)
c)
e)
6
3
4
3
1
4
1
2
1
2
2
2
2
13. Sabiendo que:
x
150º
b)
d)
L
4
1
4
2
;
4
3
1
2
2
3Tan
x
a) 0 ; 1 b) 0; 1 c) 1;
4
d) 1; 4 e) 2;
4
14. Sabiendo que: x 2
¿Cuál es la variación de :
L 3Cos
x
2
2
2
x
C.T.
; señale la variación de:
1
1?
a) 4 ; 2 b) 4 ; 2 c) 4 ; 1
d) 4 ; 1 e) 4 ; 1
15. Siendo
x
8
;
5
24
Señale la variación de:
L
2Sen
4
2x
a) 1; 2 b) 1; 4 c) 2 ; 4
d) 3 ; 6 e) 4 ; 8
16. Sabiendo que
x
17
24
Señale la variación de:
L
4Cos
;
7
8
2x
4
12
1
3
a) 1 ; 3 b) 1 ; 3 c) 1 ; 5
d) 3 ; 3 e) 3 ; 6
17. Señale Verdadero (V) o falso (F), según corresponda
en:
I. Si: 0
II. Si:
2
x
1
x
1
x
2
x
2
2
III. Si:
3
x x 2
2 1 2
1 2
Tanx
Tanx
1 2
Tanx
Tanx
Tanx
1
a) VVV b) VVF c) FFV
d) VFV e) VFF
Tanx
2
18. Hallar todos los valores que debe tomar "K" para que la
igualdad no se verifique:
Sec
2K
5
3
a) K 1 K 4 b) 1 K 4
c) 1 K 4 d) K 1 K 4
e) K 1 K 4
19. En la C.T. calcular un valor de:
3
a)
5
1
d)
5
K
x 2+y 2=1
4
b)
5
e) 1
20. Sabiendo que:
11
12
x
Señale la variación de;
C
Sen
y
4Cos
35
12
Cos
L : y-2x+1=0
1
7
c)
5
x
2
a) [ 3 ; 2] b) [ 3 ; 3] c) [ 2 ; 3]
d) [ 5 ; 6] e) [ 3 ; 5]
21. Si:
2 ; 2
; 2
Calcular la suma del máximo y mínimo valor de :
E
2Sen
3Cos
8
1
x
4Sen

a) 1 b) 2 c) 0
d) 1 e) 2
22. De las cuatro proposiciones, indicar dos que son
imposibles:
I.
2
3Sen
x 2
II.
2 2
( m n ) Cosx 2mn
III.
, m n R
( m
2
n
2
) Cscx m
2
n
2
; m n 0
IV. Secx 3
a) I y II b) I y III c) II y IV
d) II , III e) III , IV
23. Decir si son falsos (F) o verdaderos (V) los siguientes
enunciados:
I. La función Seno y Coseno son negativos en el tercer
cuadrante y crecientes en el cuarto cuadrante.
II. No existe función trigonométrica alguna de un ángulo
del segundo cuadrante que sea positivo y aumente
a medida que el ángulo crece.
III. Sólo existe una función que puede tomar el valor
de 3,8 y ser positiva en el tercer cuadrante.
a) FFF b) VFF c) VFV
d) VVV e) VVF
24. Cuando el ángulo "x" aumenta de 90º a 180º.
¿Cuál de las siguientes afirmaciones es cierta?
a) El Seno aumenta.
b) El Coseno aumenta.
c) El Cosecante aumenta.
d) La Secante disminuye.
e) La Cotangente aumenta.
25. En un círculo trigonométrico se tiene:
2
x
1
x
2
De las siguientes proposiciones:
I.
II.
1 2
Senx
Senx
Cosx
2
Cosx
1
III.
2 1
Cosx
Cosx
Es o son verdaderas:
a) Sólo I b) Sólo II
c) Sólo III d) Sólo I y II
e) Las 3 son correctas
26. En la circunferencia trigonométrica, se pide indicar el
valor de OC DB , en función del ángulo "
C
"
D
O
a) Sec Tan b) Sec Tan
c)
1 Cos
Sen
e) Sec Csc
d)
1 Cos
Sen
27. En el círculo trigonométrico, calcular el área de la región
sombreada.
a)
1
( Sen Cos 1)
2
b)
1
( Sen
Cos 1)
2
c) 1
( 1 Sen
Cos )
2
d) 1
( 1 2Cos
)
2
e) 1
( 1 2Sen
)
2
28. Calcular BQ en el círculo trigonométrico adjunto en
función de " "
B
O
O
a) 1 Sen b) 1 Sen
c) 2( 1 Sen ) d) 2(
1 Sen )
e) 2(
1 Cos )
A
Q
B

29. Evaluar:
Sen(
k ) Cos(
k )
k: número entero no negativo.
a) 1 b) 2 c) 1
d) (
k
1)
e) 1
Tan(
k
30. Si es un arco del segundo cuadrante, positivo menor
que una vuelta.
Hallar la extensión de:
Cos(
)
Si :
a)
b)
c)
d)
e)
6
1
2
1
1
2
2
3
2
4
Cos(
Cos(
Cos(
Cos(
Cos(
)
)
)
)
)
1
2
1
2
1
2
3
2
2
2
31. De las siguientes proposiciones:
I. Si : x x 0
2 1 2 entonces:
Sen x
1
Sen x
II. Si : x x 0
2 1 2 entonces:
III.
Senx
2
Senx
Cosx
2
Senx
1
Tanx
Ctgx
Es positivo en el primer y tercer cuadrante y negativo
en el segundo y cuarto cuadrante.
Son verdaderas:
a) Sólo I b) Sólo I y II c) Sólo II y III
d) Sólo III e) I , II y III
32. El mínimo valor de la función:
33. Si:
f
( x)
Tg
2
x
a) 0
1
b)
3
c) 3
d) No existe mínimo f e) 1
que:
6
;
3
( x
;
x
3
;
5
6
)
es :
para que valores de "x" se cumple
1)
Sen
2
3x
2
a)
c)
e)
14
9
16
9
10
9
;
;
;
9
14
9
16
9
10
b)
d)
13
;
9
11
;
9
34. En la figura mostrada, halle el área de la región
triangular OQP.
y
a)
c)
Sen Cos
4
Sen Cos
16
e) Sen Cos
P
Q O
b)
d)
(0;1)
9
13
9
11
Sen Cos
8
Sen
Cos
2
(1;0)
35.
En la figura siguiente, calcular el área de la región
sombreada.
y
a)
Cos(
x 2+y 2=1
)
2
c)
1
Cos(
)
3
2
e)
1
Cos(
)
2
2
b)
1
Cos(
)
2
2
d)
1
Cos(
)
2
2
36. En el círculo trigonométrico mostrado, halle el área de
la región sombreada.
y
B
C
O D A
y
x
x
x
3
x
1
3

Sen
a)
2
2
c)
e)
Tan Sen
2
2
Tan Sen
2
b)
d)
Tan 2
2
Tan Sen
2
2
37. Según la figura, sólo una de las siguientes afirmaciones
es Verdadera para:
a)
Sen2x
x
2
0
Tanx
x
2
y
B
x
O A
b) SenxCosx 2x
Tanx
c) Senx x Cosx
d) Cosx x Senx
e) SenxCosx x Tanx
38. Señale la variación de:
M
4Tan
C
D
C.T.
3
Sen
4
a) [ 5 ; 4] b) [ 4 ; 5] c) [ 3 ; 3]
d) [ 6 ; 4] e) [ 3 ; 5]
39. Señale la variación de:
Sen
2
M
x
2
Sen x
a)
d)
3
;
7
3
2
3
; 1
7
b)
e)
3
;
7
3
4
1
;
3
7 4
c)
Senx
Senx
2
;
7
40. Señale Verdadero (V) o Falso (F), según corresponda
en:
I.
II.
x ; x
1 2
0 ;
2
/ x
1
x
2
y
Sen(
Tanx )
1
Sen(
Tanx )
2
x ; x
1 2
0 ;
2
/ x
1
x
2
y
Tan(
Senx )
1
Tan(
Senx )
2
4
7
1
2
1
x
III.
x ; x
1 2
0 ;
2
/ x
1
x
2
y
Cos(
Tanx )
1
Cos(
Tanx )
2
a) VFV b) VVF c) FFV
d) FFF e) FVF
41. En la C.T. mostrada:
a)
b)
c)
d)
e)
A'
1
Tan ( Sec
2
1
Cos
2
( Sec
1
Tan ( Sec
2
1
Tan ( Sec
2
1
Cos
2
( Sec
42. En la C.T. mostrada:
Calcular: "S"
a)
d)
15
7
16
17
2
2
A'
b)
e)
S
S1
12
17
20
17
S
1
S
2
Tan
Tan
Tan
Tan
Tan
S
1
S
2
S
2
2
y
B
B'
2
1)
2
1)
2
1)
2
1)
2
1)
15
17
y
B
O
B'
c)
S2
S1
N
14
17
A x
T
S2
Q A x
2

43. Señale Verdadero (V) o Falso (F) en:
I. Cos(Sen1) < Cos(Sen2)
II. Sen(Cos2) > Sen(Cos3)
III. |Tan(Sen4)| > |Tan(Sen5)|
a) VVF b) VFV c) FFV
d) FVF e) FVV
44. Indicar Verdadero (V) o Falso (F) según corresponda
en:
I. Sec (Sen1) > Sec(Sen2)
II. Sec(Cos1) > Sec(Cos2)
III Si : Sec Tan
2
a) FFF b) FFV c) VFV
d) FVF e) VVF
45. Del gráfico mostrado, hallar las coordenadas de P.
a)
b)
c)
d)
e)
Tan
1 Tan
1
1
1
1
1
Tan
1
Tan
1
Tan
1
Tan
46. Sabiendo que:
;
Tan
1 Tan
;
Tan
1 Tan
;
Tan
1 Tan
;
Tan
1 Tan
;
Tan
1 Tan
Cot 2Cot
Señale la variación de:
L
y
3|
Sen
P
|
x 2+y 2=1
Tan
a) [0 ; 2] b) [1 ; 2] c) 1;
2
d) 1; 2 e) 1;
3
1
x
47. Sabiendo que: 3
2
2
Señale Verdadero (V) o Falso (F), según corresponda
en:
I. Tan Tan
II. Tan Sen Tan Sen
III. Tan(
2 Cos ) Tan(
2 Cos )
a) FVF b) VVF c) FFV
d) FFF e) FVV
48. En la circunferencia trigonométrica mostrada, hallar el
área de la región sombreada, si MN // AB
y
A'
N
C.T
B
B'
M
1
a) Vers Cov b) Vers Cos
2
c)
1
Vers
2
Cov
1
e)
Vers
Cos
4
d)
1
Cov
2
49. En la C.T. mostrada, calcular:
Sen
M ( 2S
) Ctg
S: área de la región sombreada.
y
x 2+y 2=1
1
a)
4
B
O
1
b)
2
2
d) 1 e)
3
A
c) 2
S
A
x
x

50. Siendo x un arco perteneciente al intervalo ( ; 0)
Además:
1
Senx
Hallar la variación de:
K
3Tan
3
2
x
2
1
a) 1; 2 b) 2 ; 2 c) ; 2
2
d)
51. Dado:
1
; 1
2
e)
;
11
6 6
2
;
3
2 2
Calcular la variación de:
2
T Cos
a)
d)
e)
3 2 3
0 ;
4
b)
1
;
2
0 ;
1
2
3
52. Si: 2
Además:
4
7
4
3
d)
Cos
Hallar la extensión de:
a)
d)
9
7
;
b)
1
15
7 ; e) 7 ;
;
6
Cos
1
1 3 2 3
;
4 4
3 3
;
1
4 2
15
4
2
Tan
c) 15
;
53. Calcular el valor de Tan , para el cual:
3 x
Csc Tan , toma su valor máximo, siendo x e y
2y
las coordenadas del punto P.
Además : 2AP = 3TP
x 2+y 2=1
T
P
y
A
x
a) 6 b)
d)
6
2
e)
54. Sabiendo que:
6
3
2 6
3
x
Señale la variación de :
L
2Csc
c)
24
3
4
;
5
24
2x
6
4
a) 2 ; 4 b) 1; 4 c) 1;
4
d) 1; 3 e) 1;
3
55. En la C.T. mostrada, las áreas de las regiones sombreadas
son iguales.
Calcular:
L
S
Tan
A'
3
Tan
M
P
y
B'
a) 2
b) 4 c) 3
d) 6 e) 8
56. En la C.T. mostrada, hallar: Tan
1
N
A
Q
Si : MP es una vertical de longitud igual al diámetro de
la C.T. y además OQ = 0,5
a)
d)
2
3
3
5
10
10
A'
C.T.
b)
e)
3
2
2
5
10
10
O
Q
B'
B
c)
y
3
4
P
M
A
x
10
x

57. Si en la C.T. mostrada, el área de la región sombreada
es igual a
Calcular:
2
2 .
L
S
2
Sec
2
Cos
M
a) 16 b) 8 c) 6
d) 18 e) 24
58. Del gráfico, hallar MN :
a)
c)
Sen
Cos
C.T.
Sen
Cos
Cos Cos
Cos Cos
y
B
A' O A
b)
d)
e) Sen ( Cos Cos )
Sen Sen
O
y
B'
M N
Sen Sen
Sen Cos
Cos
Sen
Cos
Sen
x
x
59. De la figura, "G" es el baricentro del triángulo OPQ.
Calcular la ecuación de la recta que pasa por G y por el
origen del sistema de coordenadas, en términos de
y .
P
Q
a) y Tan x
2
b) y Tan x
2
c) y Tan ( ) x
d) y Cot x
2
e) y Ctg(
) x
y
O
x 2+y 2=1
60. Si "S" representa el área de la región sombreada,
reduzca:
E
Sen
2
( S
y
Cos
3
)
O
a) 2 b) 1 c) 3
1
d) 4 e)
2
x
Sen
2
y=x2
C.T.
x

Claves
Claves
361.
362.
363.
364.
365.
366.
367.
368.
369.
370.
371.
372.
373.
374.
375.
376.
377.
378.
379.
380.
381.
382.
383.
384.
385.
386.
387.
388.
389.
390.
c
d
b
a
b
b
d
a
b
c
e
a
d
d
c
c
d
c
c
b
a
b
b
c
e
c
b
c
d
b
391.
392.
393.
394.
395.
396.
397.
398.
399.
400.
401.
402.
403.
404.
405.
406.
407.
408.
409.
410.
411.
412.
413.
414.
415.
416.
417.
418.
419.
420.
a
b
d
e
c
e
e
e
b
d
a
b
d
d
e
d
e
a
d
a
b
b
d
e
a
c
d
e
b
b

Capítulo
8
IDENTIDADES TRIGONOMÉTRICAS
DEUNA VARIABLE
* DEFINICIÓN: Son aquellas igualdades entre las razones trigonométricas de una variable; las cuales se verifican para
todo valor de la variable en que la razón trigonométrica que interviene se encuentra definida.
* CLASIFICACIÓN:
I. I. T. RECÍPROCAS:
II. I. T. POR DIVISIÓN:
III. I. T. PITÁGORAS:
SenxCscx
CosxSecx
TanxCotx
1
1
1
Cscx
Secx
Cotx
1
Senx
1
Cosx
1
Tanx
;
;
;
x
x
x
R
R
R
{n ; n
(2n
n
2
1) ;
2
Senx
Cosx
Tanx ; x R ( 2n
1 1) 1 ) ;
n Z Cotx ; x R { n ; n Z}
Cosx
2
Senx
2
Sen x
Sec
2
x
2
Csc x
2
Cos x
Tan
2
x
2
Cot x
1 ;
1 ;
1 ;
x
x
x
R
R
R
2
Sen x
Cos
2
x
n
(2n
; n
1
1
1)
2
Z
2
Cos x
Sen
2
x
; n
Z
2
Csc
x
2
Cot x
; n
Z}
2
Sec x
Z
2
Tan x
2
Cot x
2
Csc x
n
1
1
Z
2
Tan x
2
Sec x
1
1

IV. I. T. AUXILIARES:
Z
n
;
n
R
x
;
m
1
Cotx
Cscx
m
Cotx
Cscx
:
Si
Z
n
;
2
)
1
n
2
(
R
x
;
n
1
Tanx
Secx
n
Tanx
Secx
:
Si
c
b
osx
C
c
a
nx
Se
:
Entonces
b
a
c
c
bCosx
nx
aSe
:
Si
R
x
;
Senx)(1 Cosx)
2(1
)
Cosx
Senx
1
(
R
x
;
x
xCos
Sen
3
1
x
Cos
x
Sen
R
x
;
x
xCos
Sen
2
1
x
Cos
x
Sen
Z
n
;
2
n
R
x
;
x
xCsc
Sec
x
Csc
x
Sec
Z
n
;
2
n
R
x
;
SecxCscx
Cotx
Tanx
2
2
2
2
2
6
6
2
2
4
4
2
2
2
2
1.
2.
3.
4.
5.
6.
7.
8.
Cotx
Cotx
Cotx m
Cotx
Cotx
Cotx m

01. Reducir:
E = (1+Cosx)(Cscx-Ctgx)
a) 1 b) Senx c) Cosx
d) Secx e) Cscx
02. Simplificar:
E
Senx
Cscx
Cosx
Secx
Tgx
Ctgx
a) 1 b) Sec x
2 c) Csc x
2
d) Secx e) Cscx
03. Simplificar:
E
2
( Senx Cosx)
Senx.
Cosx
a) 1 b) -1 c) 2
d) -2 e) 0
04. Determinar "k" en:
a) Cos x
2
d) Cosx e) 2x
Sen
Cosx
1 Senx
1
Cosx
1 Senx
b) SenxCosx c) Senx
05. Reducir: E [ Tgx(
Ctgx 1)
Ctgx(
1 Tgx)]
Senx
a) 1 b) Ctgx c) Cosx
d) Tgx e) Secx
06. Simplificar:
E
1
1
Cosx
1
1
Cosx
a) 2 b) 2Secx c) 2Cscx
d) 2
2Sec
x e) 2
2Csc
x
07. Simplificar: E
1
Tgx
Secx Tgx
a) Secx b) Cosx c) Cscx
d) Ctgx e) 2Tgx
1 2SenxCosx
Senx
08. Simplificar: E
( x IC)
Senx
a) Senx b) Cosx c) 1
d) Tgx e) Ctgx
09. Reducir:
E
Secx.
Cscx Ctgx
Senx
a) 1 b) Senx c) Cosx
d) Secx e) Cscx
EJERCICIOS PROPUESTOS
2
k
10. Simplificar:
E
Sen
4
x
6
Sen x
Cos
4
x
6
Cos
a) 5/3 b) -1 c) 2/3
d) 3/4 e) 1/3
4 4 6 6
11. Reducir: E 3(
Sen x Cos x)
2(
Sen x Cos x)
a) 0 b) 1 c) -1
d) 2 e) -2
12. Eliminar "x" a partir de: Senx = m, Cosx = n
a) m
2
n
2
1
2
c) m
e) N.A.
2
n 3
b)
d)
2
m
2
m
1
1
2
n
2
n
13. Si: Senx+Cosx = m
Calcular: E = (1+Senx)(1+Cosx)
a)
d)
1 m
2
2
( 1
m)
2
2
b)
1 m
2
2
e) 1+m
14. Si: Tgx+Ctgx = 3
Calcular: E = Secx+Cscx
c)
( 1
a) 3 b) 9 c) 11
d) 15 e) 17
15. Reducir: E = (Tgx+Ctgx)Cosx
a) 1 b) Senx c) Cosx
d) Secx e) Cscx
5
7
2
m)
2
16. Determinar "x" para que la igualdad:
1 1
Cos
2
Tan
2
Sea una identidad
1
Cot
2
a)
2
Sen b) 2
Cos c) 2
Tan
d) Secx e) Cscx
17. Reducir: E
Cosx
Tgx
1 Senx
a) Senx b) Cscx c) Secx
d) Tgx e) Ctgx
1
x

18. Si la igualdad es una identidad
Calcular: M+N
Cscx Ctgx Cscx Ctgx
N
M 4Ctg
x
Cscx Ctgx Cscx Ctgx
a) 1 b) 2 c) 3
d) 4 e) 5
19. Hallar A en la siguiente identidad:
a) Sen x
2
d) Ctg x
2
1
1
Senx
Senx
b) Cos x
2
e) Sec x
2
20. Eliminar "x" a partir de:
Tgx + Ctgx = a
Tgx - Ctgx = b
21. Si:
2 2
a) a b 3
2 2
c) a b 4
e) 2 2
a b 8
Senx
Calcular :
1
a)
7
1
d)
12
Cosx
1
b)
6
1
e)
9
b)
a
2
A
Cscx
1
c) Tg x
2
b
2
3
d) a
2
b
2
4
7
6
C = Senx Cosx
22. Si: Tanx Cotx 3 2
Calcular:
C Sec
2
x
1
c)
14
a) 9 b) 12 c) 16
d) 18 e) 36
23. Simplificar:
C
SenxTanx
CosxCotx
Csc
2
x
Cosx
Senx
a) 1 b) Tanx c) Cotx
d) Tan x
2
24. Reducir:
e) Cot x
2
C
Sen
4
x
Senx
Cos
4
x
Cosx
a) 1 b) Senx c) Cosx
d) Senx + Cosx e) Senx - Cosx
25. Simplificar:
C
( 1
Tan
2
x)
Cos
4
x
( 1
a) 1 b)
2 2
Sen xCos x
c) Sen x
2 d) Cos x
2
e) 2
Cot
2
x)
Sen
4
x
26. Simplificar:
C = (Secx Cscx - Cotx) (Secx Cscx - Tanx)
a) 1 b) Tan x
2
c) Cot x
2
d) SenxCosx e) Secx Cscx
27. Si: Sen
4
x Cos
4
x
7
9
Calcular: 6 6
C Sen x Cos x
1
a)
3
2
d)
9
2
b)
3
4
e)
9
1
c)
9
28. Eliminar "x" de:
Senx + Cosx = m ; Tanx + Cotx = n
2
a) n(
m 1)
2
c) n(
m
2
1)
1
e) n
2
( m
2
1)
2
b) m( n 1)
2
2
d) n
2
( m
2
1)
4
29. Demostrar las siguientes igualdades:
1.1 Senx Cotx + Cosx Tanx = Senx + Cosx
1.2
2
2
Sen xCotx Cos xTanx 2SenxCosx
1.3
2
2 2
( Sec x 1)(
1 Sen x)
( Csc x 1)
( 1
2
Cos x)
1
2
2
1.4 Senx Cosx Senx Cosx
1
Tanx 1 Cotx 1
3
1.5 Senx Sen x
Cotx
3
Cosx Cos x
30. Reducir: W 3 Secx
Cscx
Cosx
Senx
a)
Cotx
2
b) Secx c) Cscx
d) Tanx e) Senx
31. Si: Sen
2
a Cos
2
a
1
2
Entonces : Tana + Cota es:
10
a)
3
b)
4 3
3
c)
13
2 10

d)
32. Si:
3 3
4
e)
( 1 Senx
Calcular: "A"
2 10
13
2
Cosx)
A(
1
a) 1 b) 2 c) 1
d) 2 e) 4
Senx)(
1
Cosx)
33. Hallar el valor numérico de la expresión:
T = (Tan35º + Tan55º) (Sen35º + Sen55º + 1)
(Cos35º + Cos55º - 1)
a) 1 b) 2 c) 2
d) 2 e) 2
34. Si: Sena Csca
5
2
Calcular : E = Cota + Cosa
a) 3 3 b) 2 3
d)
2 3
3
3
e)
3
35. Si: Sen
4
Cos
Entonces el valor de:
c)
3 3
2
Tan 1
2
, es :
Tan Cot
a) 1 b) 1 c) 3
d) 3 e) 3
3
36. Calcular:
2
Cos A
2
Sen B
Si se sabe que A y B son ángulos suplementarios
a) 1 b)
1
d)
2
e) 1
1
2
c) 0
37. Si: f ( Tan
2
x Cot
2
x)
Sec
4
x Csc
4
x
Calcular: f (2) + f (3)
a) 20 b) 21 c) 22
d) 23 e) 24
38. Si:
2
Sec x
Calcular:
2
Csc x 7
C ( Sec
2
x Tan
2
x)(
Csc
2
x
Cot
2
x)
a) 13 b) 14 c) 22
d) 16 e) 15
39. Si:
2
1 2Cos
Sen Cos
1
2
Entonces el valor de:
1
a)
4
3
d)
4
40. Reducir:
C
E
1
b)
8
1
e)
2
( Sen
6
x
Sen
Cos
6
x
Cos
3
c)
8
, es:
1)(
Tanx
a) SenxCosx b) 3SenxCosx
c) - 3SenxCosx d) - 3
e) 3
41. Si: Tanx + Cotx = 2 y
E
n n
Tan x Cot x
Tan
n
x Cot
n
x
Cotx)
Tanx
Tan
n
x Cot
n
x
Siendo "n" potencia de 2; entonces el valor de
a) 2 b) 4 c) 8
d) 16 e) 32
42.
Si: Senx Cosy = 0,5
Hallar : P
2
Cos x
2
Cos y Cosy
5
a)
4
3
d)
2
43. Calcular: Tan
3
b)
4
1
e)
4
1
c)
2
Si: aCos
4
bSen
4 ab
; a b
a b
a
a)
b
d)
a
b
44. Dado:
b
b)
a
e) ab
1
2Tanx
1 2Tany
Calcular: E = Secx + Secy
2
a)
2
2
d)
3
c)
b) 2 1 c)
e) 2 1
a
b
2Secy
2Secx
3 2
2
Cotx
2
E es :

45. El valor de "E" en la identidad:
3
Sen
2
ECos
a)
2
;
2
, es :
Sen
2
Sen b) 2
Cos c) Sen Cos
d) Cos e) Sen
46. Hallar el valor de "B" sabiendo que:
TanA
Sen
Sen
Cos
Cos
BSenA
Sen
- Cos
a) 1 b) 2 c) 3
d) 2 e) 5
47. Si: Tana
Entonces:
Es igual a:
n
m
n (2Cosa + Seca) - 2mSena
a) mCosa b) mSeca c) mn
d) nSeca e) nCosa
2 2 2
48. Si : a Cos x Sec x 2
Encontrar el valor de:
C = Senx Tanx + 2Cosx
a) a 2
2 b) a 2
2 c) a
d) a e) a
49. Si: Sec x nTanx
2
Hallar: C
a)
d)
n
n
n
n
1
2
2
1
3
Sen x
3
Cos x
( Senx Cosx)
3
b)
e)
n
n
n
n
2
1
2
1
50. Simplificar la expresión:
c)
n
n
1
2
K
1 Cosx 1 Cosx
;
1 Senx 1 Senx
a) 2 b) 2Secx
c) 2Secx d) 2Cosx
e) 2Cosx
51. Si: P, Q y R son constantes que satisfacen la relación:
P QTan
R
x
1
1
Senx
1
Cscx 1
Calcular: P . Q . R
x
3
2
52. Si:
a) 6 b) 2 c) 4
d) 8 e) 12
4
2
Calcular: C Sen Cos
y
Sen
4
a) 3 b) 5 c)
2
d)
3
3
e)
3
53. Calcular el mínimo valor de:
4
E Sec x
a) 6 b) 4 c) 8
d) 10 e) 12
54. Hallar: y = Senx Cosx
Si:Tanx - Senx = 1
a)
Cos
4
3
3
4
Csc x
1 2 b) 1 2 c) 1 2
d) 2 1 e) 2
55. Sabiendo que es un ángulo agudo el cual satisface
la ecuación:
Ctg Csc 5
Determine el valor de la expresión :
24Tg
26Sen
a) 10 b) 20 c) 15
5
d)
12
5
e)
13
56. Siendo:
Calcular:
Tanx Cotx 2
C
5
a)
3
7
b)
3
d) 3
4
e)
3
Sen
4
x Tan
2
x
57. Siendo: Senx + Cosx = n
Hallar:
C
Secx
Secx
Tanx
Tanx
1
1
a)
d)
2
n 1
2
2
n 1
b)
e)
2
n 1
1
n 1
c) 2
c)
7
9
Cos
4
xCot
2
x
Cscx
Cscx
2
2
n 1
Cotx
Cotx
1
1

58. Siendo: Tanx + Cotx = 3
Calcular:
13
a)
27
25
d)
27
59. Siendo:
Calcular:
S
19
b)
27
31
e)
27
7
Sen x
Senx
Tanx
C
7
Cos x
Cosx
29
c)
27
Cotx
Sec
5
x
Secx
a) 3( 5 6)
b) 6(
5 6)
c) 6( 3 6)
d) 3(
3 6)
e) 5(
3 6)
2
Csc
5
x
Cscx
60. Sabiendo que:
Reducir:
a)
d)
1
n 1
2
n 1
Senx
C
b)
e)
1
1
1
n 1
Cosx
2
2
n 1
Senx
Senx
n
c)
;
1
1
x
2
n 1
IVC
Cosx
Cosx

Claves
Claves
b
b
c
d
e
e
a
e
d
c
ba
c
d
e
a
c
d
d
c
d
d
b
d
a
a
b
a
-
d
b
b
b
b
c
e
d
e
c
c
b
b
e
c
e
b
d
e
c
b
c
e
c
d
b
b
b
c
b
d
31.
32.
33.
34.
35.
36.
37.
38.
39.
40.
41.
42.
43.
44.
45.
46.
47.
48.
49.
50.
51.
52.
53.
54.
55.
56.
57.
58.
59.
60.
01.
02.
03.
04.
05.
06.
07.
08.
09.
10.
11.
12.
13.
14.
15.
16.
17.
18.
19.
20.
21.
22.
23.
24.
25.
26.
27.
28.
29.
30.

Capítulo
9
I. Para la Suma:
II. Para la Diferencia:
PROPIEDADES:
I.
II.
III.
IV.
Sen(
x
Cos(
x
Tanx
Si : K
K
Si :
y)
Sen(
x
y)
Cos(
x
Tany
aSenx
2
a
y)
y)
Sen(
x y)
Cosx Cosy
2
b
bCosx
Sen(
x
IDENTIDADES TRIGONOMÉTRICAS DE
LA SUMA Y DIFERENCIA DEVARIABLES
2
Sen x
Cos
2
x
Sen(
x
Cos(
x
Tan(
x
Sen(
x
Cos(
x
Tan ( x
2
Sen y
Sen
2
y
a , b
R
) ; donde :
y)
y)
y)
y)
y)
y)
L aSenx bCosx ; a , b,
x R
L
máx
L
mín
a
2
2
a
b
2
2
b
Donde :
a b : constantes
x : variables
Senx
Cosx
Cosy
Cosy
Tanx Tany
1 Tanx Tany
Senx
Cosx
Cosy
Cosy
Tanx Tany
1 Tanx Tany
a 2 + b2
a
Seny
Senx
Seny
Senx
b
Cosx
Seny
Cosx
Seny

V.
ó
Tanx
Tanx
* Propiedades:
I.
II.
Si:
x
Si :
x
Tany
Tany
y
z
Tanx
Tanx Tany
i) Tanx Tany
ii) Ctgx · Ctgy
y
z
Tany Tan(
x
Tan(
x
y)
y)
Tan(
x
Tan(
x
y)
y)
IDENTIDADES TRIGONOMÉTRICAS PARA TRES ÁNGULOS
2
ó n
ó
;
(2n
n
Z
Tanz Tanx · Tany · Tanz
Ctgy · Ctgz Ctgz · Ctgx 1
1)
2
i) Ctgx + Ctgy + Ctgz = Ctgx · Ctgy · Ctgz
;
ii) Tan x · Tany + Tany · Tanz + Tanz · Tanx = 1
n
Z

01. Reducir:
J = Sen(30º+x)+Sen(30º-x)
a) 2Senx b) Cosx c) 2Cosx
d) Senx e) 3Senx
02. Reducir: J = Cos(45º+x)+Cos(45º-x)
a) Cosx b) Senx c) 2Cosx
2
d) 3Cosx e)
2
03. Halle un valor agudo de "x" que verifique:
Cos4x.
Cosx
Sen4x.
Senx
a) 6º b) 12º c) 18º
d) 21º e) 24º
04. Halle un valor agudo de "x" para que cumpla:
Sen4x.Cosx-Senx.Cos4x = 0,5
a) 5º b) 10º c) 15º
d) 20º e) 30º
05. Si: Tgx = 2 Tgy = 3
Calcular: Tg(x+y)
a) 1 b) -1 c) 2
d) -1/2 e) -2
06. Si: Tan
1
;
3
Tan
Calcular: Tan(
)
2
5
a) 1/7 b) -1/7 c) 1/17
d) -1/17 e) -1/19
07. Hallar el valor de: Sen7º
a)
d)
3 3
10
4
3 3
5
4
08. Calcular: Tg8º
b)
e)
3 3
10
4
3 3
2
a) 1/3 b) 1/5 c) 1/7
d) 1/9 e) 1/11
09. Si: Senx
3
5
y
Senz
4
24
25
c)
EJERCICIOS PROPUESTOS
1
2
4 3
10
3
Calcular: E =Sen(x+z); x z son agudos.
127
a)
225
117
d)
125
10. Simplificar:
M
125
b)
117
39
e)
25
117
c)
222
Cos(
30º
x)
Cos(
30º
x)
Sen(
30º
x)
Sen(
30º
x)
a) 1 b) 2 c) 3
3
d)
3
e) 3 3
11. Sabiendo que:
Sen(2x+y)Cos(x-y)+Sen(x-y)
4
Cos(2x+y) =
5
Calcular: Ctg3x
a) 3/4 b) 4/3 c) 4/5
d) 5/4 e) 3/5
12. Obtener: Sen23º
3
a)
10
4
3
3
d)
10
b)
e)
3 3
10
4
4 3
10
3
13. Del gráfico mostrado, calcular: "x".
14. Si:
x
1
4
37º
a) 17/13 b) 13/17 c) 51/13
d) 13/51 e) 3
2
Senx
3
Cosx
Calcular: Tg(45º-x)
a) 1/4 b) 1/5 c) 5/3
d) 5 e) 3/7
c)
3 3
10
4

15. Hallar: M 2Sen(
45º
x)
a) Cosx-Senx b) Senx-Cosx
c) Cosx+Senx d) 2(Cosx-Senx)
2
e)
2
16. Simplificar:
L=(Sen3x+Cos3x)(Sen2x+Cos2x)-Sen5x
a) Cosx b) Cos2x c) Cos3x
d) Cos4x e) Cos5x
17. Reducir:
18. Si:
C
Sen50º
2Sen10º
Cos40º
a) Tan40º b) Tan10º c) Cot10º
d) Cot45º e) Sen30º
5Sen(
x
Hallar : Cotx
37º
)
2Cos(
x
a) Sen37º b) Cos37º c) Sec37º
d) Csc37º e) 1
19. Simplificar:
C
Sen(
Cos(
)
)
a) Tan b) Tan c) Cot
d) Cot e) 1
20. Simplificar:
J
Sen Cos
Sen Sen
45º
)
Sen40º
Sen10º
Cos30º
Cos40º
Sen30º
Sen10º
3
a) 3 b) 1 c)
3
e) 2 e)
2 3
3
21. Siendo:
x + y = 30º ; x y = 37º
Calcular:
J = (Senx + Cosx) (Seny + Cosy)
a) 1,1 b) 1,2 c) 1,3
d) 1,4 e) 1,5
22. Del gráfico, calcular: Tan
3
a)
16
12
d)
17
A
37º
6
b)
17
14
e)
19
23. Del gráfico, calcular: Tan
A
37º
M
7
c)
19
B P C
a) 4 b) 8 c) 16
d) 9
e) 32
24. Siendo:
Calcular:
60º
C
( Cos
Cos )
2
( Sen
a) 2 3 b) 2( 2 3)
c) 3(
2 3)
d) 2 3 e) 3
25. Siendo:
x + y = 60º ;
Calcular :
3
a)
28
3 3
d)
14
M
Tany
( 1
5 3
b)
28
5 3
e)
14
3
4
TanxTany)
Tan(
x
3 3
c)
28
D
C
B
Sen )
2
y)

26. Señale el valor máximo que toma la expresión:
C = (Sen3x + Cos3x) (Sen2x Cos2x) + Senx
a) 1 b) 1
2 c) 1
d)
1
4 e)
2
3
27. Sabiendo que:
Senx - 5Cosx = 0 ; 2Seny + 3Cosy = 0
Donde: x IIIC ; y IIC
Calcular:
L = Sen(x + y) + Cos(x y)
a)
d)
3
13
3
13
2
2
b)
e)
6
13
5
13
1
2
2
c)
6
13
28. Si: Tan( a
Calcular:
b c)
3
5
y Tanb = 3
Tan (a b + c)
a)
d)
6
7
29
17
21
b)
7
e)
11
27
27
c)
11
29. Si: A + B + C = 180º
El valor de:
E = TanA+ TanB+TanC TanA TanB TanC
a) 1 b) 1 c) 2
d) 0 e) 2
30. Si x e y son ángulos complementarios (x > 0º),
encontrar el valor de "m" de modo que se verifique la
identidad.
1
m
Tg
y
2
a) 1 b) 2 c)
d)
y
Tan e)
2
1
y
Tan
x
Tan
2 2
Tan
Tan
x
2
31. Hallar TanA en un ABC, cuyos ángulos cumplen:
SenA = nSenB SenC
CosA = nCosB CosC
a) n b)
d) n 1
2
2
n c) n 1
e) n + 1
2
x
2
32. Simplificar:
P
Tan
1
1
Ctg(
Tan
Ctg(
a) Tan Tan b) Tan Tan
c) Ctg d) Tan
e) Ctg
33. Calcular el valor de:
Tan13º + Tan32º + Tan13º Tan32º
a) 2 2 b) 1 2
1 2
c)
2
e) 1
2
d)
2
34. Simplificar la siguiente expresión:
a)
Cos7a
Sen3a
Tan5a
b)
d) Ctg3a e)
1
Tan2a
Cos3a
Sen7a
Sen3a
Sen7a
35.
A partir de la figura, hallar "x".
30º
2 3
a) 3 b) 3 c) 4
d) 6 e) 7
36. Calcular: Sen75º + Cos75º
6
a)
2
6
d)
3
b)
e)
2 3
3
6
2
2
Ctg5a
)
c) Ctg7a
c)
6
2
37. Si: Tan ( x y)
a
a
b
b
; Tan(y z) = 1
Entonces: Tan(x z) es igual a:
a
a)
b
b
b)
a
c)
a
a
b
b
1
)
Ctg 2a
2
7
x

a
d)
a
b
b
e)
a b
a
38. Los ángulos , y satisfacen la relación:
Tan
Tan
Hallar la suma de:
(K : Número entero)
Tan
a) 0 b) 2k c) k
2
d)
4
k
e) k
Tan Tan Tan
39. En la siguiente figura, la medida del lado x es:
a) 4 6 b) 4 23 c) 4 13
d) 3 17 e) 3 6
40. Hallar el valor de:
Sabiendo que:
a)
( 2
2
6)
( Cosx
x
7
Rad
12
b)
c) 0 d)
e)
3 2
2
x
Seny)
Cos
,
( 3
y
4
3 3
4
3)
y x
2
5
Rad
12
41. El valor de la expresión:
(Tan80º Tan10º) Ctg70º es :
a) 1 b) 1 c) 2
d) 2 e) 0
42. Nos situamos a una distancia de 500 metros de un
edificio de 100m de altura, que tiene 25 pisos idénticos.
Hallar el valor de la Tangente del ángulo mostrado.
4
6
2
43. Si:
5
a)
3143
25
d)
3143
Sen(
y
2t)
500
3143
b)
500
36
e)
3143
4
5
;
Seny
1
c)
274
x
5
;
10mo. piso
9no. piso
2
y 2t
Expresar x en términos de Sen 2t y Cos2t solamente:
a) x = 4Cos2t + 3Sen2t
b) x = 3Cos2t 4Sen2t
c) x = Cos2t Sen2t
d) x = 2Sen2t 3Cos2t
e) x = 2Cos2t + 3Sen2t
44. En la figura mostrada, se tiene un trapecio isósceles en
el que la longitud de la base menor es igual a la de su
altura y la longitud de su base mayor es igual a la de su
diagonal.
Hallar: Tan
B C
A
4
a) 2 b)
3
3
d)
4
1
e)
3
1
c)
7
45. Hallar el valor aproximado de:
7 2
a)
10
2
d)
10
D
9 2
b)
10
3 2
e)
10
Cos
2
4º
Cos
2
86º
5 2
c)
10
D

46. En un triángulo ABC, se cumple:
SenC
2Sen(
A
B)
TanB 3 3 2 6
Hallar el valor del ángulo BAC.
a) 3
47. Si:
3
d)
10
Hallar:
5
b)
12
2
e)
3
Tan
Ctg
14
5
28
c) 6
a) 3 b) 2 c) 1
1
d)
2
1
e)
3
48. Determinar el mayor valor de A y el menor valor de B
tal que:
A
Senx
x
x
2Cosx
a) 3 y 3 b) 5 y 5
1
2
c) 3 y 3 d) 2 5 y 2 5
e) 2 2 y 2 2
49. En un triángulo rectángulo ABC recto en C, calcular el
valor de M.
M
1
Tan
A
2
1
Tan
B
2
a) 0 b) 1 c) 2
d) 3 e) 4
B
1
Tan
C
2
50. En la figura adjunta, la longitud del segmento AB es:
C
A B
a) 2 3 b) 3 3 c) 4 3
d) 5 3 e) 6 3
3
4
2
51. En la identidad trigonométrica:
2Senx
Determinar: Tan
a)
3
d)
2
2
13
2
b)
3
e)
13
3
52. En la siguiente figura:
MC
3
CB
4
Calcular: Tgx
13
a)
4
24
d)
5
AB
8
3Cosx
y
D
c)
MC
kCos(
x
3
13
MD
M
A B
b)
22
7
e)
17
9
x
8
c)
3
53. Si: Sen 2Sen
y Cos 3Cos
Hallar el valor de: Cos(
)
5
a)
7
5
d)
7
b)
6
e)
7
3
7
3
c)
7
54. En la figura mostrada, calcular: Tan
1
a)
2
5
d)
2
3
b) 2 c)
2
1
e)
6
55. Si : 60 º , el valor de la expresión:
A ( Cos Cos
2
) ( Sen Sen
2
) es
a) 2
3
b)
4
d) 0
1
e)
2
c) 1
)
3
2
1
C

56. Si:
57. Si:
Tan(x + 3y) = 5 y Tan(2y + x) = 4
Entonces el valor de Ctgy es :
a) 20 b) 21 c) 18
d) 14 e) 15
Tan(2a + b) = 8 y Tan(a + 2b) = 2
Entonces: Tan(a b) es:
12
a)
17
6
d)
17
4
b)
17
e) 10
c) 6
58. Del gráfico calcular el valor mínimo de: Cot
Si:
a)
d)
AE
2
10
6
2
10
9
ED
3
DC
E
D
A B
b)
e)
3
10
5
3 10
10
c)
2
10
3
C
59. Del gráfico, calcular: Tanx
17
a)
241
17
d)
195
60. Siendo:
x
45º
C
A D 2 B
21
b)
241
21
e)
195
Cos
Cos
23
c)
241
2
m
Sen Sen m
¿Cuál es la variación de "m" para que se cumplan las 2
relaciones anteriores?
a)
b)
c)
d)
e)
5
2
5
2
5
2
5
2
5
2
1
;
1
;
1
;
1
;
;
5 1
2
5 1
2
5 1
2
5 1
2
5 2
2
1
F
4

Claves
Claves
b
c
b
b
b
d
a
c
d
c
a
e
c
b
a
a
e
c
a
c
c
b
e
e
b
a
d
c
d
b
e
d
e
d
b
a
a
e
a
b
c
d
a
c
a
a
a
b
e
e
b
b
d
a
c
b
d
d
b
d
01.
02.
03.
04.
05.
06.
07.
08.
09.
10.
11.
12.
13.
14.
15.
16.
17.
18.
19.
20.
21.
22.
23.
24.
25.
26.
27.
28.
29.
30.
31.
32.
33.
34.
35.
36.
37.
38.
39.
40.
41.
42.
43.
44.
45.
46.
47.
48.
49.
50.
51.
52.
53.
54.
55.
56.
57.
58.
59.
60.

Capítulo
IDENTIDADES TRIGONOMÉTRICAS
DELA VARIABLEDOBLE
10
x
Tan
1
Tanx
2
x
2
Tan
x
Sen
x
Cos
Cos2x
2SenxCosx
Sen2x
2x
de
Tangente
2x
de
Coseno
2x
de
Seno
2
2
2
También :
x
Sen
2
1
x
2
Cos
2
1
x
Cos
2
x
2
Cos
2
* Fórmulas de Degradación :
x
4
Cos
x
2
Cos
4
3
x
Cos
8
x
2
Cos
1
x
Cos
2
x
4
Cos
x
2
Cos
4
3
x
Sen
8
x
2
Cos
1
x
Sen
2
4
2
4
2
* Propiedades :
I.
x
2
Cot
2
Tanx
Cotx x
2
Csc
4
x
Csc
x
Sec
2
2
2
x
2
Csc
2
Tanx
Cotx
II.
x
2
Sen
1
)
Cosx
Senx
(
x
2
Sen
1
)
Cosx
Senx
(
2
2
III.
Cosx
Senx
x
2
Sen
1
Cosx
Senx
x
2
Sen
1
IV.
1
x
2
Sec
Tanx
x
2
Tan
1
x
2
Sec
xTanx
2
Tan
2
Cos
1
Sec
Sec
Sec
Sec
Sec
Sec
x
Cos2
Cos2
Cos2
1 2
Cos
Cos
Cos
Sec
Sec
Sec
Sec
Sec
Sec
Sec
Sec
Sec
Sec
Sec
Sec
Sec

* Triángulo del Ángulo Doble :
1
2
Tan
2
1
2
Tan
2Tan
Sen2
Cos2
2Tan
2
1 Tan
1
1
2
Tan
2
Tan
IDENTIDADES TRIGONOMÉTRICAS DE LA VARIABLE MITAD
Sen
x
2
Seno de
x
2
1
Cosx
2
Cos
x
2
Coseno de
x
2
1
Cosx
2
x
Donde el signo ( ) dependerá del cuadrante en el que se ubique
2
Tangente de
x
2
x
Tan
2
Cscx
Cotx
x
Cot
2
Cscx
Tangente de
x
2
Tan
x
2
Cotangente de
x
2
Cotx
1
1
Cosx
Cosx

01. Si " " es un ángulo agudo y
Calcular: " Sen 2 ".
a)
d)
4
.
9
9
4
5
5
02. Simplificar:
03. Si:
04. Si:
05. Si:
06. Si:
07. Si:
E
b)
2
9
5
e)
4
8Sen
5
. Cos
c)
Sen
2
.
3
1
9
. Cos2
5
. Cos4
a) Sen2 b) Sen8 c) Sen16
d) Sen4 e) Sen32
Sen
2
, calcular: Cos2
5
a) 2/5 b) 3/5 c) 4/5
d) -3/5 e) -4/5
Cos
1
, calcular: Cos2
3
a) -1/3 b) 1/3 c) 2/3
3
d) -2/3 e)
3
Tg
1
, calcular: Tg 2 .
2
a) 1/3 b) 2/3 c) 4/3
d) 5/3 e) 7/3
Tg
3
, hallar: Sen2
2
a) 11/13 b) 12/13 c) 14/15
d) 13/15 e) 11/15
Tg
1
, determinar: Cos2
5
a) 1/3 b) -1/3 c) 2/3
d) -2/3 e) 3/4
08. Si: Sen
7
90º
180º
25
Calcular: Sen2
EJERCICIOS PROPUESTOS
336
a)
625
d)
336
625
236
b)
625
e)
436
625
c)
236
625
09. Si: Cos
5
180º
270º
13
Calcule: Sen2
a)
120
169
60
d)
169
120
b)
169
e)
140
169
10. Si: Tgx+Ctgx = n
¿A qué es igual Sen2x?
c)
a) 2/n b) n/2 c) 2n
d) 1/2n e) 1/n
11. Si: Cosx
2
90º
x 180º
3
x
Calcule el valor de: Sen
2
6
a)
6
d)
6
12
b)
e)
6
6
2 6
3
6
c)
12
60
169
12. Si: Sen
7
180º
270º
25
Calcule el valor de:
2
a)
10
7 2
d)
10
3 2
b)
10
e)
Sen
2
5 2
10
5 2
c)
10
13. Si: Cos
3
90º
180º
4
Calcule el valor de:
2
a)
2
d)
2
3
2
b)
3
e)
Cos
2
2
4
2
c)
4

1
14. Si: Cos , calcule: Cos
2 3
a) 1/3 b) 2/3 c) 3/4
d) -1/3 e) -2/3
15. Si: Cosx
1
90º
x 180º
3
x
Calcular el valor de: Tg
2
a) 3 2 b) 2 c) -3 2
d) - 2 e) 5 2
16. Si: Tg
20
180º
270º
21
Calcule:
Tg
2
a) -5/4 b) -5/2 c) 3/4
d) -3/4 e) 1
17. A qué es igual:
a)
d)
Tg
x
b)
2
Ctg
x
e)
8
E
Csc
x
4
Ctg
x
c)
2
Ctg
x
8
18. ¿A qué es igual: Ctg8º?
Ctg
x
4
Tg
x
8
a) 3 b) 5 c) 7
d) 9 e) 11
19. Reducir: E = Sec40º-Tg40º
a) Tg25º b) Ctg25º c) -Tg25º
d) -Ctg25º e) 1
20. Si:
2
Calcule:
E
Cos
7.
Sen
3
4
a) 0 b) 1 c) 2
d) 2 e) 2 2
21. Reducir :
2
Cos
2
H = (Tanx + Cotx) Sen2x
a) 1 b) 2 c) 3
22. Si :
3
d) 4 e)
2
Sen2x
Calcule :
7
a)
9
d)
23. Si :
2
9
2
3
b)
e)
el valor de Sen2
3
a)
2
E
7
9
2
7
Sen
6
Sec
2
b)
d) 1 e) 1
es :
3 1
2
4
Sen x
Cos
6
Csc
2
4
Cos x
2
c)
9
1
c) 1
24. Simplificar la función f definida por :
f
( x)
2
Sec x
2
Csc x
a) 2Sec2x b) 2Sec2x
c) 2Csc2x d) Secx + Cscx
e) 2Csc2x
25. Indique la expresión simplificada de :
a)
c)
e)
26. Si :
M
1
1
Cos2
Cos4
2
4Cos b)
1
Sen
2
2
2
4Sen
Cos
5
;
13
Halle : Cos
2
a)
d)
2
13
3
13
b)
e)
d)
3
13
5
26
;
1
Cos
2
2
1
Csc
2
4
3
2
c)
;
K
2
2
2
13
3
16
;
x
,
K
Z

27. Señale el valor de
a)
c)
e)
2
2
2
2
4
2
28. Reducir :
29. Si :
2
1
2
H
Cos
8
b)
d)
1
2
2
2
2
2
1
1 Cos24º
2
2
a) Cos6º b) Sen6º c) Sen3º
d) Cos3º e) Sen12º
hallar :
Cos
4
y 180º 270º ,
5
Tan
2
4
a) 3 b)
5
d)
5
4
e) 1
c) 3
30. Si : Tan
x
n , donde x ,
2
entonces cuál de las siguientes alternativas es la correcta.
a)
b)
c)
d)
e)
Senx
Senx
Senx
Senx
Senx
31. Sabiendo que :
1 n
2
; Cosx
2
1 n
1 x
2
; Cosx
2
1 x
2n
; Cosx
2
1 n
2x
; Cosx
2
1 x
2
3Sen
x
Halle el valor de :
2
1 n
; Cosx
2
1 n
2n
2
1 n
2x
2
1 x
1
1
1
1
2
7Cos
x
n
2
2
n
x
2
2
x
2n
2
1 n
a
M = 3a 2b
a) 9 b) 15 c) 13
d) 11 e) 7
bCos2x
32. Reducir :
M = Csc2x + Csc4x + Csc8x + Cot8x
a) Tanx b) Cotx c)
d)
33. Reducir :
a)
d)
Cot
x
e)
2
Tan
x
2
2
b)
Tan
x
e)
2
Cot
x
4
R
Tan
x
2
CscxCot
x
2
CscxTan
x
2
Tan
x
2
2
Cot
x
2
2
c)
1
1
Cot
x
2
2
34. Si se tiene un triángulo rectángulo ABC, recto en B con
5
A ángulo menor, la relación de catetos es .
7
Se tiene la relación :
E = 7Cos2A + 5Sen2A
Determinar el valor de E.
a) 4 b) 5 c) 6
d) 7 e) 8
35.
Encontrar aproximadamente el valor de :
a)
1
2 3
3
1
c)
1
2
3
3
e) 2 3 2 6
Tan
25
24
b)
1
6 2
5
d)
2
36. Sea : a b c
Simplificar la siguiente expresión :
Sen(3a + 2b + 2c) Sen(a + 2b + 2c) + Cos(b + c)
Cos(b + 2a + c)
a) 1 b) 0 c) 1
d) Cos2a e) Cos2b
37. Si A, B y C son los ángulos internos de un triángulo y
1
Sen(A + B) Cos(A + B) =
2
¿Cuánto vale 1 + TanC?
a) 0 b) 1 c) 2
d) 1
1
e)
2
2
2
3
3

38.
U
N
I
SecA
SenA
CosA
Cos
A
2
Cos
A
4
Cos
A
2K
Sen
A
2
Sen
A
4
Sen
A
2K
K 1
Simplificar la expresión :
a) SenA CosA
b)
Sen
A
K
U
Cos
A
K
c) 1 Sen
A
K
d) CosA SenA
e)
Sen
A
K
Cos
A
K
N
I
2
2
2
SenA
Sen
A
2
1
CosA
Sen
A
K
39. Hallar la suma de los valores máximos y mínimos de la
siguiente expresión :
E
ACos
2
A, B son constantes reales.
x
2
B
a) B b) A c)
2
A
d)
2
40. Si :
e) 0
Sen 2x
3
;
5
calcular : 4 4
Cos x Sen x
4
a) 1 b)
5
3
d) 1 e)
5
x 0 ; ,
4
41. Halle el valor de la expresión :
W
c)
BCosx
3
5
Sen20º
3Cos20º
Sen40º
Cos40º
a) 2 b) 4 c) 1
1
d)
2
1
e)
4
42. Halle "m" en la identidad :
Sen2xSen
4
x
Sen
a) 2 b) 4 c) 8
d) 6 e) 3
43. El valor de :
( Cosa
En función de
4
2
Cosb)
a) 2Sen a b
b)
2
x
( Sena
Sen
a b
es:
2
2
4Sen
c) Sen
a b
d) Sen
2
2
e)
2Sen
2
a b
2
Sen(
mx)
m
a b
2
a b
2
44. Si : Tanx + Cotx 2 = Sen2y A
A
( Seny
( Seny
Cosy)
2
2
Cosy)
( Seny
( Seny
hallar :
4 4
S Tan x Cot x
a) 4 b) Sen 2y
4
a) 4
d) 1
e) 2
45. Sabiendo que :
c) Sen2y
2
Senb)
SenxSeny
3
4
; x y ,
hallar : Cos2(x y)
1
a)
4
d)
7
8
46. Si : KSen
2
b)
7
e)
8
1
4
Cos
2
Siendo : Sen 0
Será :
a) ( K
2
K
2
)
P
2
c)
1 Sen
2
Sen
b) K
K
1
2
Csc
c) 1
K K
d) 1
K K
e)
K
K
1
1
Cosy)
2
2
Cosy)
,

47. Expresar en función de Tanx, la expresión:
E
a)
2(
Tan2x
Sec2x)
Cot2x
1
1
Tanx
Tanx
2
b)
2
Sec 2x
1
1
Tanx
Tanx
c) 1 2Tanx d) Tanx + 1
e) 1 Tanx
48. Si : Tan
m
; n 0 ,
n
2
Tan 2x
entonces el valor de nCos2 mSen2
es :
a) m + n b) 2m + n c) 2m n
d) m e) n
49. Si :
Y Tan
2
xSec
2
x
2 2
Cot xCsc x ,
entonces :
a) y 16Csc
4
x
3Sec
2
x
4
c) y Csc16x
d) y
4
e) y Csc 2x
3Csc
2
x
b) y 16Csc
4
2 x
16Cscx
4
50. Sea la ecuación :
mSen
x
2
nCos
x
2
p 0
¿Bajo cuál de las siguientes relaciones entre m, n y p, el
valor de
Tan
x
es único?
4
2 2 2
a) m n p b)
2
m
2
p
2
n
2 2 2
c) n p m d) m
2
n
2
2p
e) 2 2
m n p
51. Si x es un ángulo en el primer cuadrante y
a
b
expresión :
1
2
Tanx ; encontrar el valor de la siguiente
a)
d)
2a
a b
2a
2a
b
E
b)
e)
Sen2x
Cscx Senx
b
a b
ab
a b
c)
1
2b
a 2b
a
b
52. El valor de X al simplificar la expresión :
X
1
1
Tan
Tan
a) 1 Sen2
b) 1 Sen2
c) 1 d) 1
e) Sen2
53. Si : Tan ( A 45º
)
a
a
1
,
1
hallar : Sen2A
2a
a) 2
1 a
2a
d) 2
1 a
b)
e)
2
1 Sen2
1 Sen2
2a
a
2 c) 2
a 1 1 a
a
2
a
54. Si : Tan(x + 45º) = n ; n 0 ,
calcular : E = Sec2x Tan2x
a)
d)
1
n b) 2n c)
1
2n e) 2
n
55. La expresión :
1
Cos
1 Sen
a)
Tan
b) Tan
4
c) 2Tan d) Tan
4
2
e) Tan
2
4
56. Hallar el valor de :
Tan2A
Sabiendo que :
TanA TanB = 1
Sen2A
2
4Sen
2
A
n
2
es equivalente a:
Tan2B
a) 2 b) 1 c) 0
d) 1 e) 2
57. Reducir la expresión :
S
1
2
2
Sen
2
Sen (
150º
)
4
4
Tan
5
4
2
Sen (
a) Cos( 30º
2 ) b) Sen(
30º
2 )
c) Sen2 d) Cos2
e) Sen(
60º
2 )
150º
)

58. Calcular :
E
2
a)
2
d)
Sen
4
16
1
Cos
2
1
2
3
8
b)
3
e)
2
59. La siguiente suma :
F
1
2
Tan
x
2
Sen
4
2
2
....
1
Tan
n
2
x
n
2
Es igual a :
3
16
a)
1
Cot
x
Cotx
n n
2 2
b)
1
Cot
x
Cotx
2 n
2
c) Cotx
d)
1
Cot
x
Cotx
2 n
2
e)
n n
2 Cot(
2 x)
Cotx
1
Cos
2
3
c)
4
1
Tan
x
2 2
2 2
8
......
60. Si :
Cos
Cos
Cos
Halle : R
a)
c)
e)
Tan1º
Tan2º
Tan1º
Tan4º
Tan1º
Tan6º
Sen7º
Sen1º
Tan7º
Tan1º
Cos7º
Cos3º
Tan Tan Tan
2 2
b)
d)
2
Cos7º
Cos1º
Sen9º
Sen2º

Claves
Claves
a
a
a
d
a
b
b
a
a
a
a
a
d
b
b
c
b
b
d
a
d
d
a
c
d
c
e
d
c
b
e
c
a
b
c
c
a
b
d
d
a
b
d
c
c
b
e
c
b
e
c
a
a
c
b
a
b
e
b
e
01.
02.
03.
04.
05.
06.
07.
08.
09.
10.
11.
12.
13.
14.
15.
16.
17.
18.
19.
20.
21.
22.
23.
24.
25.
26.
27.
28.
29.
30.
31.
32.
33.
34.
35.
36.
37.
38.
39.
40.
41.
42.
43.
44.
45.
46.
47.
48.
49.
50.
51.
52.
53.
54.
55.
56.
57.
58.
59.
60.

Capítulo
11
Sen3x
FÓRMULAS ESPECIALES:
Sen3x
DEGRADACIONES:
PROPIEDADES :
3Senx
IDENTIDADES TRIGONOMÉTRICAS
DELA VARIABLETRIPLE
Seno de 3x Coseno de 3x Tangente de 3x
Senx(
2Cos2x
3
4Sen
x
3
4Sen
x
Senx
Cosx
Tanx
Cos3x
11) 1 )
Cos
3x
3Senx
Sen(
60º
Cos(
60º
Tan ( 60º
Sen3x
3
4Cos
x
Cosx(
2Cos2x
x)
Sen(
60º
x)
Cos(
60º
x)
Tan ( 60º
3Cosx
3
4Cos 4 4Cos 4 Cos
x
x)
x)
x)
1)
Tan 3x
Tan 3x
3Cosx
1
Sen3x
4
1
Cos3x
4
Tan 3x
3
3Tanx
Tan x
2
1 3Tan
x
Tanx
Cos3x
Tanx + Tan(60º+x) + Tan(120º+x) = 3Tan3x
2Cos2x
2Cos2x
1
1

01.Señala el equivalente de la expresión:
Sen3x
3
Cos x
Sen
3
x
3
Cos x
a) Tgx b) Secx c) Cscx
d) Ctgx e) N.A.
02. Simplificar:
E = (Tg2A+TgA)(Cos3A+CosA)Csc3A
a) 1 b) 2 c) 3
d) 4 e) N.A.
03. La expresión que da Cos3x en términos de Cosx es:
a) 3Cosx+4Cos 3 x b) 4Cosx3Cos 3 x
c) 3Cosx-4cos 3 x d) 4Cos3x-3Cosx
e) 3Cos3x-4Cosx
04. El valor de la expresión:
05. Si:
Sen3a
Sena
Cos3a
Cosa
a) 5 b) 4 c) 3
d) 2 e) 1
Tgx
1
. Calcular: Tg3x.
11
a) 3,07 b) 0,27 c) 3,27
d) 32 e) 0,21
06. Sen2a = Cos3a, 0

16. Calcular:
Tan9º+Cot9º-Tan27º-Cot27º
a) 2 b) 4 c) 6
d) 0 e) 8
17. Calcular:
3
a)
2
d)
6
4
18. Simplificar:
2
Cos85º(1+2Sen80º)
1
b)
2
e)
5 1
4
c)
6
4
Tan3 (2Cos2 -1)-(2Cos2 +1)Tan an
a) Tan b) Cot c) 0
d) Tan3 e) Cot3
19. Calcular:
3Cos 2 10º.Sec 2 50º.Sec 2 70º
a) 64 b) 9/64 c) 1/64
d) 192 e) 64/9
20. Calcular:
Sec
2
9
8Cos
a) 1 b) 2 c) 3
d) 5 e) 6
2
2
9
21. Siendo : Cot 2 2 ; " " agudo.
Calcular : Sen3
7
a)
9
d)
23
27
b)
7
9
17
e)
27
22. Si : Cos 2x
1
,
3
hallar : Cos6x
22
a)
27
17
d)
27
23
b)
27
e)
23. Hallar : Sen 111º
8
a)
125
23
27
108
b)
125
23
c)
27
c)
22
27
117
c)
125
2
107
d)
125
24. Sabiendo que :
calcular :
a)
d)
17 2
36
23 2
36
25. Siendo :
Sen
Calcular : C
1
a)
3
d)
1
3
9
e)
125
b)
e)
Cot
C
17 2
36
7 2
36
2
3
Cos3
Cos
2
b)
9
e)
26. Sabiendo que :
2
9
2
2
Sen3
c)
c)
Cos
1
,
3 2
calcular : P Sen3
Csc
2
a)
9
d)
2
9
4
b)
9
e)
4
9
c)
;
Sec
23 2
36
7
9
7
9
27. Señale el valor de "Senx", si :
Sen2x = Cos3x
a)
5 1
4
b)
c) 1
d) a y c son respuestas.
e) a, b y c son respuestas.
28. Reducir :
A
5
4
Sen3x
Senx
1
Cos3x
Cosx
a) Cosx b) Sen2x c) Sen4x
d) 4Cos2x e) 2
IIC ,

29. Siendo : Sen
1
,
3
calcular : L
Cos3
Cos
11
a)
3
7
b)
2
5
d) 2 e)
9
30. Reducir :
c)
11
3
C = (Cos3x + 2Cosx) Tanx
a) Sen3x Cosx b) Tan3x
c) Sen3x d) Cos3x Senx
e) Cot3x
31. Si : Sen3x = 0,25 Senx,
2
calcule : K 5Tan
x 1
a) 2 b) 4 c) 6
d) 8 e) 12
32. Si : Tan3x = 5Tanx,
calcule : |Tan2x|
2
a) 7 b) 14 c)
5
7
d)
3
e) 5
33. Al calcular el valor de :
obtenemos :
1 3
F ,
Sen10º
Cos10º
a) 1 b) 2 c) 3
d) 5 e) 4
34. El valor de :
E = Cos80º Cos20º Cos40º es:
3
a) 2 b)
4
1
d)
2
35. Simplificar :
1
e)
8
E
1
c) 4
Sen20º
3Sen20º
a) 2Tan20º b) Tan40º c) 2Tan40º
d) Tan20º e) Sec20º
36. Simplificar :
C
Sen3x
2Senx
Cos3x
a) Tanx b) Tanx c) Cotx
d) Cotx e) Tan x
2
37. Siendo :
Sen3x
3
Sen x
Cos3x
calcular : L = Tan3x Cotx
3
Cos x
6
a)
13
3
d)
13
b)
e)
3
13
6
13
c)
38. Calcular el máximo valor de :
M
3
Tan3x
. Cot x
;
12
13
a) 17 12 2 b) 17 12 2
c) 12 17 2 d) 12 17 2
e) 5 2
39. Si : Sen
18º
5 1
,
4
x
1
3
,
0 ;
hallar el valor de M,
si :
MSec15º Sec9º = Sen15º Sen9º
a)
c)
1
8 5
1
4 5
8
4
e) 4 5 1
b)
d)
8
5
1
5 1
8
40. Al simplificar la expresión :
E = Sen6º Sen54º Sen66º
Obtenemos :
a) Sen12º b) 2Sen6º
c) Sen18º d) 2Sen12º
e)
Sen18º
4
41. Calcular el valor aproximado de la expresión :
S = Csc27º Sec27º
a) 3 5 b) 3 5
2

c) 2( 3 5)
d) 5 5
e)
3 5
2
42. El valor de :
Es igual a :
x
1
4Cos20º
3
a) Cot10º b) Tan10º c) Cot20º
d) Tan20º e) 2Tan10º
43. Calcular el valor de ,.
Sen3
2
Cos Sen Cos3
2
Sen Cos
( Sen Cos
2
)
a) 1 b) 1 c) 2
1
d) 2 e)
2
44. En el triángulo de la figura, hallar el ángulo
que a sea doble de b.
, para
a)
c)
e)
a
ArcCos
3
b)
2
ArcCos
1
d)
4
ArcCos
3
4
45. Calcule:
1
a)
2
3
d)
2
b b
x y z
M
3
b)
4
1
e)
4
ArcCos
2
3
ArcCos
1
2
a
3
Sen 17º
3
Cos 13º
Sen17º
Cos13º
3
c)
8
46. Si :
Sen3x Cscx + Cos3x Secx = K Cosp . x,
calcular : K + p
a) 2 b) 3 c) 4
d) 6 e) 8
47. Si : Cos39º = nCos13º,
halle : Tan 13º
2
a)
d)
48. Si :
3
1
2
1
halle :
n
n
n
n
b)
e)
en términos de "n"
2
1
1
3
n
n
n
n
Tan 3x
n 1 ,
Tanx n 1
c)
3
1
Senx en términos de "n"
Sen3x
1 2
a) n + 1 b) ( n 1)
c)
n
d) n 1 e)
( n
1)
Sen3x
Sen3y
Sen3z
49. Sabiendo que : n
Senx Seny Senz
,
hallar :
L
Cos3x
Cosx
1
Cos3y
Cosy
n
n
Cos3z
Cosz
a) n + 3 b) n 3 c) n + 6
d) n 6 e) 2n 6
50.
Del gráfico, hallar la medida del ángulo " "
a
17º
43º
13º
4a
a) 39º b) 17º c) 36º
d) 51º e) 48º
51. El valor de :
a)
128
3
2Sec
2 2 2
10º
Sec 50º
Sec 70º
es :
9
b)
64
64
d) 192 e)
9
1
c)
64
52 El valor de :
G = Cot24º Cot57º Cot24º Cot33º
a) 2 b) 3 c) 2
d) 1 e) 1

53. Hallar el valor de la expresión :
M
2 2 2
Tan 20º
Tan 40º
Tan 80º
a) 12 b) 9 c) 21
d) 24 e) 33
54. En el gráfico :
calcular " "
a)
c)
e)
A
ArcCos
6
b)
7
ArcCos
9
d)
10
ArcCos
5
6
S
1
S
2
S1
55. Del gráfico, calcular : Sen3
3
a)
4
2
d)
3
A
3
b)
8
1
e)
6
4
2
2
3
B
95
84
2
,
D
ArcCos
8
9
ArcCos
10
11
E
F
1
c)
3
56. Desde un punto en tierra, se divisa lo alto de una torre;
con un ángulo de elevación " ". Si nos acercamos
una distancia igual a la altura de la torre, el ángulo de
elevación es " 90 º 2 ".
Calcular el valor de :
L
Sec2
a) 1 b) 2 c) 3
d) 4 e) 6
2
S2
Tan
57. Calcular :
L = Tan130º Tan10º + Tan70º Tan130º
Tan10º Tan70º
3
C
D
C
a) 3 b) 3 c) 2
d) 2 e) 6
x
58. Del gráfico, hallar :
y
A
B
5º 45º 80º 20º
D E
x y
a) 2Csc5º b) 2Csc10º
c)
2
Csc5º
2
e)
2
Csc5º
4
59. Del gráfico, hallar : x
a)
c)
e)
m
2
n
2
m
2
m n
m
m n
m
m n
n
d)
2
Csc10º
2
2
m
n
A B
b)
d)
n
2
n
2
m n
m
m n
n
60. Del gráfico, hallar la longitud de CD
A
6º
16
a) 1,23 b) 2,23 c) 1,36
d) 3,23 e) 2,32
B
C
D
x
C
C
24º 36º
D
E

Claves
Claves
a
b
d
d
b
b
e
c
d
d
d
c
c
c
b
b
d
c
a
e
c
e
c
d
c
c
a
e
e
c
c
d
e
e
b
b
d
a
a
e
c
c
c
e
b
d
e
b
d
a
a
c
e
a
a
a
a
e
c
a
01.
02.
03.
04.
05.
06.
07.
08.
09.
10.
11.
12.
13.
14.
15.
16.
17.
18.
19.
20.
21.
22.
23.
24.
25.
26.
27.
28.
29.
30.
31.
32.
33.
34.
35.
36.
37.
38.
39.
40.
41.
42.
43.
44.
45.
46.
47.
48.
49.
50.
51.
52.
53.
54.
55.
56.
57.
58.
59.
60.

Capítulo
12
TRANSFORMACIONES TRIGONOMÉTRICAS
IDENTIDADES PARA LA SUMA Y PRODUCTO DE SENOS Y/O COSENOS
CASO I : Para la suma o diferencia de dos Senos o Cosenos a producto.
Demostración :
Conocemos :
Si sumamos (1) + (2) obtenemos :
Hacemos un cambio de variable :
Luego en (*) :
Sea:
Sen(
x
Sen(
x
Cos(
x
Cos(
x
SenA
SenA
CosA
CosB
y)
y)
y)
y)
SenB
SenB
CosB
CosA
2Sen
2Sen
2Cos
2Sen
SenxCosy
SenxCosy
CosxCosy
CosxCosy
A B
2
A B
2
A B
2
A B
2
Cos
Cos
Cos
Sen
CosxSeny
CosxSeny
SenxSeny
SenxSeny
A B
2
A B
2
A B
2
A B
2
.......... ........ (1)
.......... ........ (2)
.......... ........ (3)
.......... ........ (4)
Sen(x + y) + Sen(x - y) = 2Senx Cosy ........... (*)
x
x
y
y
SenA
A
B
obtenemos :
SenB
2Sen
x
A B
2
A B
2
Cos
Las restantes identidades pueden verificarse en forma análoga.
CASO II
Para el producto de dos términos, Senos y/o Cosenos a suma o diferencia.
Siendo : x y
2 Senx Cosy = Sen(x + y) + Sen(x y)
2 Seny Cosx = Sen(x + y) Sen(x y)
2 Cosx Cosy = Cos(x + y) + Cos(x y)
2 Senx Seny = Cos(x y) Cos(x + y)
y
A B
2
A B
2

SERIES TRIGONOMÉTRICAS :
Para la suma de Senos o Cosenos cuyos ángulos están en progresión aritmética.
n
Sen(
K 1
n
Cos(
K 1
( K
( K
Propiedad n Z
1)
r)
1)
r)
Productorias n Z
Sen
nr
2
Sen
r
2
Sen
nr
2
Sen
r
2
Sen
Cos
Cos
2n
2
Cos
2n
Sen
2n
Cos
2n
Tan
2n
P
1
1
P
U
2
U
2
3
Cos
2n
4
Cos
2n
Sen
2
1 2n
Cos
2
1 2n
Tan
2
1 2n
1
1
Donde :
5
Cos
2n
6
Cos
2n
Sen
3
1 22n
2
n
Cos
1
3
2n
Tan
3
1 2n
n : # de términos
r : razón de la P.A.
P : primer ángulo
U : último ángulo
1
1
....
....
.... Sen
n
1 2n
....
Cos
1 ....
1 ....
1 ....Cos Cos ....
.... Tan
n
1 2
n
( 2n
1)
Cos
2n
1
n
2n
2n
Cos
2n
1
1
1
1
2n
1
n
2
1
n
2
2n
1
1
2
1
2

01. Reducir:
E
Sen5x
Senx
Cos2x
a) 2Sen3xCos2x b) 2Sen3x+1
c) 2Sen3x d) 2
e) 2Cos3x
02. Reducir:
E
Sen4x
Sen2x
Sen3xCosx
a) 1 b) 2 c) 3
d) 4 e) 5
03. Reducir:
E
Sen40º
Sen20º
Cos10º
a) 1 b) 1/2 c) 1/4
d) 2Sen10º e) Cos10º
04. Reducir:
E
Cos3x
Cosx
Cos2x.
Cosx
a) 1 b) 2 c) Sen3x
d) Sen2x e) Cosx
05. Reducir:
E
Sen7x
Sen5x
Sen6xCosx
a) 1 b) 2 c) 3
d) Senx e) Cosx
06. Reducir:
E
Sen5x
Sen3x
2Cos4
xCosx
a) 1 b) 2 c) Senx
d) Tanx e) Cotx
07. Reducir:
E
Sen17º
Sen3º
2Sen7º
Sen10º
a) 1 b) 2 c) Tan10º
d) Cot10º e) Tan3º
08. Reducir:
E
Sen20º
Cos50º
Sen80º
a) 1 b) -1 c) 2
d) -2 e) 3
EJERCICIOS PROPUESTOS
09. Reducir:
E
Sen80º
Sen20º
Cos20º
Cos80º
a) 1 b) 2 c) Tan50º
3
d) 3 e)
3
10. Reducir:
E = (Sen70º+Cos70º).Sec25º
2
a) 1 b) 2 c)
2
d) 1/2 e) 2
11. Simplificar:
E
Sen3x
Cos3x
Senx
Cosx
a) Tanx b) Cotx c) Tan2x
d) Cot2x e) 2
12. Simplificar:
E
Sen7x
Cos3x
Sen3x
Cos7x
a) Tan2x b) Cot2x c) Tan4x
d) Cot4x e) 1
13. Simplificar:
E
Cosx Cos3x
Sen2x
a) Senx b) -Senx c) 2Senx
d) -2Senx e) Cos2x
14. Simplificar:
E
Senx
Cosx
Sen3x
Cos3x
Sen5x
Cos5x
a) Tanx b) Tan2x c) Tan3x
d) Tan4x e) Tan5x
15. Transformar a producto:
E = Sen2x + Sen4x + Sen6x + Sen8x
a) Sen5xCos2xCosx b) 4Sen5xCos2xCosx
c) 4Cos5xCos2xCosx d) Cos5xCos2xCosx
e) 4Sen2xCos3xCosx
16. Reduzca:
G
Sen70º
Sen10º
Cos70º
Cos10º
a) Tan40º b) Cot40º c) 3
3
d)
3
e) Tan20º

17. Reduzca :
H
Sen7x
Senx
Cosx Cos7x
a) Tan3x b) Cot3x c) Tan4x
d) Cot4x e) Cot4x
18. Simplifique :
G
Sen20º
Sen40º
Sen60º
Cos10º
Cos30º
Cos50º
a) 3Sen40º b)
3
Sen40º
2
c)
2
Sen40º
3
e)
3
Sen40º
4
d) 2Sen40º
19. Transforme a producto :
R = Sen3x + Sen5x + Sen9x + Sen11x
a) 4 Cosx . Cos3x . Sen7x
b) 2 Cosx . Cos3x . Sen7x
c) 4 Cos2x . Cos3x . Sen7x
d) 2 Cos2x . Cosx . Sen7x
e) 2 Cos2x . Cos3x . Sen7x
20. En un triángulo ABC; reducir :
L
Sen2A
Sen2B
Sen(
A B)
a) 2CosC b) 2CosC c) 2SenC
d) 2SenC e) CosC
21. La expresión :
Es igual a :
Senx
Cosx
Seny
Cosy
x y
a) Tan b) Sen
2
c) Cos
x y
2
d) Cot
e)
Sen(
x
Cos(
x
y)
y)
22. La expresión :
es igual a :
a)
Sen4x
Sen6x
Senx
Sen2x
b) 1
x y
2
x y
2
Sen3x
Sen4x
Cos2x
c)
Sen3x
e) Sen2x
d)
Sen2x
Sen3x
23. La expresión :
Senx + Sen3x + Sen5x + Sen7x
es igual a :
a) Sen4x + Sen12x
b) Sen16x
c) 4Senx Sen2x Cos4x
d) Sen4x
e) 4Cosx Cos2x Sen4x
24. Transformar en producto la siguiente expresión :
Cos4x
Cos8x
2
2
4Sen
x
2
a) Cos2x Cos3x b) 4Cos2xSen
3x
2
2
c) 2Cos2xSen
2x
d) 4Cos2xCos
3x
2
e) 4Cos4
xCos 2x
25. Transformar en producto la expresión :
E = SenA + Sen2A + Sen3A
a) 4Sen
3A
Cos
A
CosA
2 2
b)
c)
d)
SenACos
3A
2
2
Cos
3A
SenASen
A
2 2
4Cos
3A
SenASen
A
2 2
e) 3Cos
3A
Cos2ACosA
2
26. La expresión :
Sen4x
es igual a :
2
Sen 2x
CosxSenx
Cosx
Senx
TanxSenx
a) Tanx b) Cos2x Cos3x
c) 2Senx Cos3x d) Sen2x Sen3x
e) 2Sen3x Cosx
27. Reducir:
E = 2Sen3xCos2x - Senx
a) Senx b) Sen3x c) Sen4x
d) Sen5x e) Sen6x

28. Simplificar:
E = 2Sen5xCos3x-Sen8x
a) Senx b) Sen2x c) Sen3x
d) Sen4x e) Sen5x
29. Reducir:
E = 2SenxCos3x+Sen2x
a) 1 b) -1 c) Sen2x
d) Sen4x e) Cos2x
30. Reducir:
E = 2Sen5xCosx-Sen6x
a) Sen2x b) Sen4x c) 0
d) 1 e) Senx
31. Reducir: E = 2Cos40ºCos20º-Sen70º
3
a) 1 b) 1/2 c)
2
d) 3 e) 0
32. Reducir: E = 2sen4xCos2x-Sen6x
a) Senx b) Sen2x c) Sen3x
d) Sen5x e) Sen4x
33. Reducir: A = 2Cos5xCosx-Cos6x
a) Cos2x b) Cos3x c) Cos4x
d) Cos5x e) Cos8x
34. Reducir: E = 2Sen5xSen3x+Cos8x
a) Sen2x b) Cos2x c) Cos3x
d) Cos4x e) Cos6x
35. Reducir:
E = 2Cos50ºCos10º-Cos40º
3
a) 1/2 b)
2
d) 3 e) 2 3
36. Reducir:
c) 1
E = 2Sen3xSenx+Cos4x
a) Cosx b) Cos2x c) Cos3x
d) Cos4x e) Cos6x
37. Calcular:
E
2Sen3xCosx
Sen4x
2Sen2x
cos 4x
Sen6x
a) 1 b) -1 c) 0
d) Sen6x e) Sen4x
38. Calcular:
E
1
4Cos80º
Sen70º
2Cos80º
a) -1 b) 1/2 c) 1
d) -1/2 e) 0
39. Simplificar:
E
Cos4
Cos3
Cos5
Sen2
a) Sen2 b) Sen c) Cos
d) Cos2 e) Sen4
40. Reducir:
E
Cos2
2Sen2x.
Cos3x
Senx
2Sen4x.
Cosx Sen3x
a) 1 b) -1 c) Sen5x
Sen5x
d)
Senx
41. Reduzca :
e) Cosx
H
2Sen3xCosx
Sen4x
2Cos5xCos4
x Cos9x
a) 2Senx b) 2Cosx c) Senx
d) Cosx e)
1
Cosx
2
42. Si :
P(x) = Sen3x Cos2x + Sen3x Cos4x Senx Cos6x
Calcule : P
30
1
a) 1 b)
2
3
d) 3 e)
2
c) 2
43. Halle el valor de la expresión :
2
a)
4
6
d)
3
R
2Sen40º
Cos20º
Sen20º
2Cos35º
Cos10º
Cos25º
3
b)
4
2
e)
6
6
c)
2

44. Si se define la función :
f
( x)
halle : f ( x)
máx
1
a) 1 b)
2
3
d)
4
1
e)
4
Cos
45. Del gráfico, calcule "x"
(Cos40º = 0,766)
2
9
4
x
3
c)
2
D
Cos
A
50º
10º
x B
a) 2,532 b) 3,156 c) 2,216
d) 3,108 e) 2,748
46. Si el ángulo A mide rad
13
hallar el valor de :
a) 1 b)
1
d)
2
e)
F
1
2
3
2
,
9
CosACos10A
Cos2A
Cos4
A
2
c)
3
47. Dada la expresión 2 Sen
x
Cos2x
,
2
indicar si es igual a :
a)
b)
c)
d)
e)
Sen
Sen
Sen
Sen
Cos
5x
2
5x
4
5x
2
5x
4
5x
4
Sen
Sen
Sen
Sen
Cos
3x
2
3x
4
3x
2
3x
4
3x
4
x
C
,
48. Cuál de las siguientes expresiones equivale a : 2Cos6x
Senx
a) Cos7x + Sen5x
b) Cos7x + Senx
c) Sen7x + Sen5x
d) Sen7x + Cosx
e) Sen7x Sen5x
49. La suma de los senos de tres arcos en progresión
aritmética de razón
2
3
es :
50. Si :
a) 1 b) 0 c) 1
2
d)
3
e) No se puede determinar.
Sen
Cos
( a
2
2
b
Sen
Cos
0)
a
b
Calcular : Cos(
)
2ab
a) 2 2
a b
2 2
a 3b
c) 2 2
a b
2 2
b a
e)
2ab
51. Si :
Senx + Seny = a
Cosx Cosy = b
calcular :
1
M
a
a)
b
a
1
d)
b
a
2ab
b) 2 2
a b
2 2
b a
d) 2 2
b a
aSen(
x y)
Cos(
x
Sen(
x y)
aCos(
x
b) ab c) a b
a
e)
b
52. Si : Sen2x + Sen2z = 0 y z x ,
4
los valores de
2
Cos z
2
Cos x serán :
a)
b)
c)
2 2
2
,
1
2
,
2
1
2 1
2
2
2
2
1 , 1 2
2
y)
y)

d)
e)
1
2
, 1 2
2
2
1 ,
2
2 2
2
53. Transforme a producto :
W
Cos2
Cos2(
Cos2
)
Cos2
a) 2Cos(
) Cos(
) Cos(
)
b) 4Cos(
) Cos(
) Cos(
)
c) 2Sen(
) Cos(
) Cos(
)
d) 4Cos(
) Sen(
) Cos(
)
e) 4Cos(
) Cos(
) Cos(
)
54. Si : Cos2x Cos4x Cos8x = 0,5,
calcule :
A
Tan7x
Tan9x
a) 0,6 b) 0,8 c) 1,6
d) 1,8 e) 2,4
55. Calcular el valor de la siguiente expresión:
1
Sec80º
2
2Sen70º
a) Tan10º b) Cot10º c) 1
d) 1 e)
1
Cot10º
2
56. La función trigonométrica :
es equivalente a :
a)
b)
c)
( Cosx
Sen
3
2
x
( CosxCos 2x)
Sen
f(
x)
CosxCos 2xCos
Tanx
Cosx
SenxSen2x
Cos2x)(
CosxCos2x)
3
2
x
x
2
Tan2x
Cos2x
d)
e)
Cos2xCosxCos
Sen
3
2
x
Sen 2xCos
2x
Cosx Cos 2x
x
2
57. Si : Seny = 2Sen(2x + y),
entonces : Tan (x + y) es igual a :
a) 2Tanx b) 4Tanx c) 5Tanx
d) 3Tanx e) Tanx
58. Si : 2Sen5x = 3Sen3x,
hallar :
M
2
25Cot
4x
a) 2 b) 1 c) 2
d) 1 e) 0
59. Simplificar :
a) 2Tan20º b) Tan40º
c) 2Tan40º d) Tan20º
e) Sec20º
E
1
2
Cot x
Sen20º
3Sen20º
60.
Calcular el valor aproximado de la expresión :
S = Csc27º Sec27º
a) 3 5 b) 2 3 5
c)
3 5 d) 3 5
2
e) 5 5

Claves
Claves
c
b
a
b
b
d
d
a
d
b
a
b
c
c
b
a
d
c
a
b
a
d
e
d
a
e
d
b
d
b
b
b
c
b
a
b
b
c
b
a
a
b
c
d
a
b
c
e
b
d
d
e
b
a
d
c
d
e
b
b
01.
02.
03.
04.
05.
06.
07.
08.
09.
10.
11.
12.
13.
14.
15.
16.
17.
18.
19.
20.
21.
22.
23.
24.
25.
26.
27.
28.
29.
30.
31.
32.
33.
34.
35.
36.
37.
38.
39.
40.
41.
42.
43.
44.
45.
46.
47.
48.
49.
50.
51.
52.
53.
54.
55.
56.
57.
58.
59.
60.
4

Capítulo
13
FUNCIONES TRIGONOMÉTRICAS REALES
DEVARIABLEREAL
INTRODUCCIÓN
Dentro del análisis matemático, el concepto de función es materia de un largo estudio debido a su flexibilidad para
representar vía modelos matemáticos una cierta realidad que se desea investigar, ya sea para prevenir u optimizar.
En ese contexto las funciones trigonométricas, debido a sus características de periodicidad, juegan un rol importante en la
representación de fenómenos periódicos, como las transmisiones radiales por ejemplo; por ello su estudio es imprescindible.
DEFINICIÓN DE FUNCIÓN TRIGONOMÉTRICA
Por ejemplo :
Si queremos algunos pares ordenados :
F.T. = {(x ;y) / y = R.T. (x) ; x D(F.T.)}
F.
T.(
Tangente)
F.
T.(
Tangente)
(0
; 0)
,
{( x;
y)
/
; 1
4
y
,
Tanx ; x
;
3
3
,
2
3
D(Tan) }
CONSIDERACIÓN I :
Para el análisis de cada una de las funciones trigonométricas, tendremos que recordar las representaciones, en la circunferencia
trigonométrica, de las Razones Trigonométricas, así como algunas propiedades adicionales.
A’
Sen
Sen
Cuadro de Variaciones I
B
B’
y
Sen
Sen
Sen
Cos
Tan
A
x
0
0
0
1
A’
2
1
0
Cos
Cos
2
1
0
B
B’
0
y
1
0
Cos
Cos
0
0
1
A
3
2
1
0
x
;
A’
3
2
0
1
3
2
1
0
0
, ...
B
B’
y
Tan
A
x
Tan

Además, no olvide que en la C.T. mostrada, los arcos con extremo en :
y
B
A es de la forma :
A’ A
Pero si debido a alguna condición; puede estar ubicado en :
B’
A o A' ; es de la forma : n ; n Z
B o B' ; es de la forma : ( 2n
1)
; n Z
2
A,A' ; B o B' ; es de la forma :
n
2
; n Z
Por ejemplo : si nos pidiesen hallar " " que cumple :
x
B es de la forma :
2n
A' es de la forma : (2n
B' es de la forma : (4n
(4n 1)
2
1)
Sen 0 " " tiene su extremo en A o A' n ; n Z
Sen 1 " " tiene su extremo en B
Cos 0 " " tiene su extremo en B o B'
3)
2
; n
; n
;
;
n
n
( 4n
1)
; n Z
2
( 2n
1)
; n Z
2
Cos 1 " " tiene su extremo en A' ( 2n
1)
; n Z
Sen 2 0 " 2 " tiene su extremo en A o A' 2 n
ANÁLISIS DE LAS FUNCIONES TRIGONOMÉTRICAS
I. FUNCIÓN TRIGONOMÉTRICA SENO
;
n
2
F.T.(Sen) = {(x ;y) / y = Senx ; x D(Sen)}
Por lo visto en la representación y de acuerdo al cuadro de variaciones, tenemos :
2
Senx
1
Senx
2
1
y
0
1
Gráfica que recibe el nombre de sinusoide; desde el cual podemos afirmar :
2
x
1
x
2
3
2
; n Z
2 5
2
3 x
Z
Z
Z
Z

* D(Sen) = R
mín
* R(Sen) [ 1 ; 1]
1 Senx 1
máx
* Es una función continua en R.
* Es una función creciente y decreciente.
* Es una función periódica : T 2 (periodo principal)
* Es una función impar : Sen( x) = Senx
* No es inyectiva.
II. FUNCIÓN TRIGONOMÉTRICA COSENO
F.T.(Cos) = {(x ;y) / y = Cosx ; x D(Cos)}
Por lo visto en la representación y de acuerdo al cuadro de variaciones, tenemos :
y
2
1
Cosx
1
0
Cosx
2
1
Gráfica que recibe el nombre de cosinusoide; ; desde el cual podemos afirmar :
* D (Cos) = R
mín
* R(Cos) [ 1 ; 1]
1 Cosx 1
máx
* Es una función continua en R.
* Es una función creciente y decreciente.
* Es una función par : Cos( x) = Cosx
* Es una función periódica : T 2 (periodo principal)
* No es inyectiva.
x
1
III. FUNCIÓN TRIGONOMÉTRICA TANGENTE
2
x
2
3
2
2
5
2
F.T.(Tan) = {(x ; y) / y = Tanx ; x D(Tan)}
De acuerdo a la representación en la C.T. y el cuadro de variaciones; y con el detalle adicional que la tangente no se
define para todo arco cuyo extremo coincide con B o B', (en la C.T.), es decir, los arcos de la forma ( 2n
pertenecen al dominio de la función.
y
1)
2
, n Z no
2
Tan
0
Tan
2
Asíntotas
3
2
2 5
2
3
x
3
x

A la curva se le va a denominar tangentoide; y de allí podremos afirmar :
*
D(
Tan)
R
( 2n
1)
2
; n
* R(
Tan)
R Tanx
*
*
No se define en ( 2n
1)
; n Z
2
Es una función creciente en cada cuadrante.
* Es una función impar : Tan( x) = Tanx
* Es una función periódica : T (período principal)
* No es inyectiva.
CONSIDERACIÓN II :
A’
Z
y
Cot B Cot
B’
A
A’
x
Csc
B’
Nótese de los gráficos, aparte de las representaciones de las R.T.; que la cotangente, secante y cosecante no se definen
respectivamente, para arcos cuyo extremo coincide con :
A y A' n ; n Z
B y B' ( 2n
1)
2
; n Z
A y A' n ; n Z
Cuadro de variaciones II :
Cot
Sec
Csc
0
1
2
0
2
0
1 1
IV. FUNCIÓN TRIGONOMÉTRICA COTANGENTE
F.
T.(
Cot)
{( x ; y) /
y
B
1
y
Csc
A’
1
Sec
A
3
2
x
B
3
2
0 0
1
Cotx ; x
1
y
B’
D(Cot) }
2
1
Sec
A
x

De acuerdo a lo visto en la representación y en el cuadro de variaciones, tendremos :
2
Cot
0
y
Cot
2
Asíntotas
Curva que recibe el nombre de cotangentoide; de donde podemos afirmar :
* D(
Cot)
R { n ; n Z}
* R(
Cot)
R Cotx
* No se define en n ; n Z
* Es una función decreciente en cada cuadrante.
* Es una función impar : Cot( x) = Cotx
* Es una función periódica : T (periodo principal)
* No es inyectiva.
V. FUNCIÓN TRIGONOMÉTRICA SECANTE NT TE
F.
T.(
Sec)
Según la representación y variación, tendremos :
y
2
1
0
1
2
{( {(x {( x ; y)
/ y
Curva denominada secantoide, de donde afirmamos :
*
D(
Sec)
R
( 2n
1)
2
1
; n
* R(
Sec)
; 1 ; Secx 1 o Secx 1
*
*
No se define en ( 2n
1)
; n Z
2
Es una función creciente y decreciente
* Es una función par : Sec( x) = Secx
* Es una función periódica : T 2 (período principal)
* No es inyectiva.
Z
3
2
Secx
2
3
2
;
x
5 3
2
2
D(Sec) }
Asíntota
x
x

VI. FUNCIÓN TRIGONOMÉTRICA COSECANTE
F.
T(
Csc)
2
y
0
(x ; y) /
1
2
1
y Cscx ; x
Curva a la que se denomina cosecantoide, de la cual afirmaremos :
* D(
Csc)
R { n ; n Z}
* R(
Csc)
; 1 1 ; Cscx 1 o Cscx 1
* No se define en n ; n Z
* Es una función creciente y decreciente
* Esunafunción par : Csc( x) = Cscx
* Es una función periódica : T 2 (periodo principal)
* No es inyectiva.
3
2
2
D(Csc)
5
2
Asíntota
x

01. Halle la suma del máximo y mínimo valor de la función:
f(x) = 3+Senx
a) 5 b) 6 c) 7
d) 8 e) 9
02. Indique el mínimo valor que asume la función:
g(x) = 4-Cos 2 x
a) 1 b) 3 c) 5
d) 6 e) 7
03. Determine el dominio de la función: f(
x)
4
2
Senx
a) R {
n
/ n Z}
b) R
2
c) R - {0} d) R { n / n Z}
e) R
{( 2n
1)
/ n
3
Z}
04. Determine el dominio de la función: HH(
H ( x
)
4
Cos(
1
)
x
a) R b) R - {0} c) R - {1}
d) R { n / n Z}
e) R - {2}
05. Graficar la función:
y = F(x) = 2Senx; x [ 0;
2 ]
a) b)
y
1
-1
/2
3 /2 2
c) d)
y
2
-2
y
e)
1
0
2
2
x
x
x
y
1
-1
y
2
-2
EJERCICIOS PROPUESTOS
2
2
x
x
06. Graficar: y=f(x) = |Senx|; x [ 0;
2 ]
y
1
-1
y
1
-1
a) b)
2
c) d)
e) N.A.
2
x
x
07. Dadas las funciones f y g definidas por: f(x)=2Cosx y
g(x) = 1+Cosx.
Hallar un intervalo donde f(x) < g(x)
a) b) c) < ;2 >
2
3
d) < ; > e)
2 2
08. Determine el rango de la función: H(x)=3+3Cos 2 x
a) [2,5] b) [2,4] c) [3,6]
d) R e) [0,3]
09. Determine el rango de la función: F(x)=4-2Sen 2 x
a) [1,2] b) [2,4] c) [3,7]
d) [-1,1] e) R
10. Determine el rango de: g(x)=8Sen 2 x-1
a) [-2,5] b) [-1,7] c) [2,4]
d) [-3,3] e) R
11. Determine el periodo de: y=f(x)=4Cos3x+7
2
a) 2 b)
3
3
d)
2
e)
y
1
0
y
0
c) 3
2
2
x
x

12. ¿Cuál es el dominio de la función: f definida por:
f ( x)
2Sen(
x ) 1 ?
a) R b) R-{1} c) [-1;1]
d) R-{0} e) [0;+ >
13. ¿Cuál es el dominio de la función g definida por:
g ( x)
3Cos(
1
) 2 ?
x
a) R b) R + {0} c) [-1;1]
d) R-{1} e)
14. Determine el rango de la función f definida por:
f(
x)
2
2Cos
x Cosx 1 .
a) [ 2;
9
] b) [ 2;
7
] c) [ 4;
7
]
8 16
8
d) [ 4;
7
] e) [
3
;
7
]
4 2 8
15. Si f es una función definida por:
f(
x)
Sen
2
x
2Senx
5
2
Determine el valor de: E 2f
4f
máx mín
a) 14 b) 15 c) 16
d) 17 e) 18
16. Graficar: y = |Sen4x|
Indicar su periodo.
a)
8
b)
4
d) e) 2
c) 2
17. Determine la extensión de la función:
18. Si:
H(
x)
CosxTanx Senx
Tanx
a) [-2;2] b) [-1;1] c) [1;2]
d) [-1;5] e) R
F(
x)
| Senx|
1
. Determine el rango de F.
2
Sen x 1
a)
d) e) R-{0}
19. Si: g ( x)
2 | Cosx | . Determine el rango de g.
a) [ 0;
2]
b) [ 2;
2]
c) [ 2;
3]
d) [-1;1] e) [ 1;
3]
20. Hallar el rango de la función f definida por:
f(
x)
Senx
Senx
2
;
3
x
[ 0;
2
a) [ 0,
1 / 2]
b) [ 1/
2,
3 / 4]
c) R
d) [ 0,
2]
e) [ 1,
1]
21. Señale Verdadero (V) o Falso (F) según corresponda
en :
I. La función : y = f(x) = Senx, posee un máximo en
0 ;
]
II. La función y = f(x) = Senx, es inyectiva en
2
;
2
III. La función : y = f(x) = Senx, es impar.
a) VVV b) VVF c) FVV
d) VFV e) VFF
22. Señale Verdadero (V) o Falso (F) según corresponda
en :
I. La función : y = f(x) = Cosx, es inyectiva en
; 2
II. La función : y = f(x) = Cosx, es creciente en 0 ;
III. La función : y = f(x) = Cosx, es par.
a) VVV b) VFV c) VVF
d) VFF
e) FVV
23. Señale Verdadero (V) o Falso (F) según corresponda
en :
I. La función : y = f(x) = Tanx, tiene dominio :
R
( 2n
1)
2
; n
Z
II. La función : y = f(x) = Tanx, es creciente en
2
;
3
2
III. La función : y = f(x) = Tanx, es impar.
a) VVV b) VVF c) FVV
d) VFV e) VFF
24. Se define la función :
y = f(x) = Tan2x + 1
¿Cuál será su dominio?
a) R
n
; n Z
2
b) R ( 2n
1)
; n Z
c) R ( 2n
1)
; n Z
4
d) R n ; n Z

e) R 2n
; n Z
25. Señale el dominio de la función :
y
g(
x)
a) R b) R
Senx
Cosx
1
1
( 2n
;
(n
1)
2
c) R n d) R ( 2n
1)
e) R
n
2
26. Señale el rango de la función :
y
h(
x)
2
2Sen
x
a) [0 ; 2] b) 3 ; 13
c) 0 ; 13 d) [2 ; 3]
e) 2 ; 13
Z)
2
3Cos
x
27. Determine el rango de "F".
F(x) = 3 + SenxCosx
a) [2 ; 4] b) [3 ; 4]
c)
5
2
;
e) [5 ; 7]
7
2
28. Dada la función :
d)
h(x)
Determine su rango
a)
c)
e)
3
2
;
2 ;
7
2
7
2
1 ;
5
4
3
2
;
5
2
2
Cos x
b) 1 ; 2
d)
5
4
;
7
2
Senx
29. Se define la función :
y=f(x) = 2Csc3x 1
¿Cuál es su dominio?
a) R 3n
; n Z
b) R
n
; n Z
3
c) R
n
; n Z
6
d) R ( 2n
1)
; n Z
3
e) R ( 2n
1)
; n Z
6
30. ¿Cuál es el máximo valor que puede tomar la función :
f(x) = Sen(x 90º) en el intervalo [0 ; 72º]?
a) Sen ( 20º) b) 1
c)
1
2
e) Sen 18º
d) 0,55
31. Si consideramos M el valor máximo que asume la
función :
f(x) = (3 Senx) (3 + Senx)
y N el valor mínimo que asume la función:
g(
x)
Luego : M . N resulta :
Cosx
1
3
a) 8 b) 8 c) 1
d) 1 e) 0
Cosx
32. Para qué valores de x,
Cosx
0 x 2 se cumple Senx >
a) 0 x
b) 0
4
c) 0 x
5
d) 0
4
e)
4
x
5
4
33. Si f es la función definida por :
f(
x)
x
x
3
4
7
4
2SenxCosx
1
1 SenxCosx
1
3
x ; 0 entonces el rango de f es :
2
a)
;
4 b)
5
; 1
3
3
c) 4
; d)
3
e)
4
; 1
3
1 ;
34. ¿Cuál o cuáles de las funciones dadas son inyectivas?
I. f(x) = Senx 0 x
II. g(x) = Cosx 0 x
III. h(x) = Cotx 0 x
a) Sólo I b) Sólo II
c) Sólo III d) II y III
e) I y II
4
3

35. Si f(x) = aSen(kx) ; g(x) = aCos(kx) son funciones
cuyas gráficas se muestran en la siguiente figura.
Calcular las coordenadas del punto P.
2
2
g(x)
a) ; 2
3
c)
3
;
2
2
e)
5
; 2
3
f(x)
P
2
3
b)
5
; 2
12
d)
5
12
36. Determinar el dominio máximo de la función :
f(
x)
2
a) n ; n Z
4
b) n ; n Z
2
c) n ; n Z
4
d) ( 2n
1)
; n Z
4
e) ( 2n
1)
; n Z
2
37. Dadas las proposiciones :
;
2
Sen x
2
2
4
Sen x
I. La función Senx es creciente en 0 ;
1
4
II. La función Cosx es decreciente en 0 ;
III. La función Tanx es creciente en
¿Cuáles de ellas son verdaderas?
a) Sólo I b) Sólo II
c) Sólo III d) I y II
e) II y III
38. El valor máximo que toma la función :
f(
x)
2
3Sen
x
2
4Cos
x
0 ;
2
, x R , es :
a) 3 b) 4 c) 5
d) 6 e) 7
39. El mayor valor que toma la función :
f(x) = Cos2x + 3Sen2x + 2 es :
a) 2 10 b) 6
c) 3
e) 5
10 d) 1 10
40. Hallar el mínimo valor de :
17
a)
18
45
d)
46
M
35
b)
36
23
e)
24
10
2
9Cos
x
27
c)
28
Senx
41. Hallar el rango de f(x) = | Cotx| Senx
a) 1 ; 1 b) 1 ; 1
c) 1 ; 1 d) 1 ; 1
e) R 1 ; 1
42. Si m y M son los valores mínimo y máximo
respectivamente, de la función :
f(
x)
Entonces m + M es :
6
Sen x
6
Cos x
1
a)
2
b) 1
3
c)
2
d) 2
5
e)
4
43. Si P = (x ; 1 a) es un punto que pertenece a la gráfica
de la función Seno,
hallar :
A = Senx (1 Senx) (Cscx)
a) 1 a
a
b)
2
d) a e) a 1
1
c)
a
44. El mínimo valor de la función :
f(
x)
2
Tan x ;
1
a) 0 b) c) 3
3
d) No existe el mínimo valor de f
e) 1
x
3
;
5
6

45. Dadas las funciones :
y = f(x) = Sen2x |Senx| + Cos2x |Cosx|
y = g(x) = Senx
Se afirma :
I. En
II. En
0 ;
2
III. En
3
; 2
2
tos.
, sus gráficas se intersectan en 1 punto.
;
3
, sus gráficas se intersecan en 1 punto.
2
IV. El periodo principal de "f" es .
¿Cuántas son verdaderas?
a) 1 b) 2 c) 3
d) Todas e) Ninguna
46. Dada la función :
h(
x)
Señale el dominio.
a) 2n
; (2n 1)
, sus gráficas se intersectan en 2 pun-
Senx
b) ( 4n
1)
; (2n 1)
2
c) ( 4n
3)
; 2n 2
2
d)
e)
2n
(4n
; (4n
1)
2
1)
2
; (4n
3)
2
Cosx ; n
47. Señalar cuál es la proposición falsa:
FUNCIÓN
)
a
b) Tanx
c)
d)
e)
Senx
Cotx
Cosx
Secx
R
DOMINIO
R
R
( 2n
R
R
n
1)
2
( n Z
R
R
R
Z
RANGO
[ 1 ; 1]
[ 1 ; 1]
)
48. En el intervalo [ 0 ; 2 ] el siguiente gráfico corresponde
a :
y
3
2
3
a) Senx + 2Cosx
b) 4Cosx + 3Senx
c) 2(Senx + Cosx)
d) 3Senx + 2Cosx
e) 3(Senx + Cosx)
2
49. La diferencia entre el valor máximo y el valor mínimo
de la función :
f(x) = |Senx| + |Cosx|
Es aproximadamente igual a :
3
2
a) 0,41 b) 0,42 c) 0,44
d) 0,46 e) 0,91
50. Hallar el máximo valor de :
E
Senx
Senx
Para :
x
4
a)
2 b) 1 c) 0
d) 1 e) 2
;
4
Cosx
Cosx
51. Si : f(x) = 1 Sen|x|
Indicar Verdadero (V) o Falso (F) para las siguientes
proposiciones:
I. f(x) es creciente en
2
;
3
2
II. f(x) es decreciente en
3
2
III. f(x) tiene como rango [0 ; 2]
a) VFF b) VFV c) VVF
d) VVV e) FVV
52. Si R es el rango de la función f y
f(
x)
Cos6x
Cos4x
Entonces, podemos afirmar :
;
2
Cos2x
a) R 0 ; 1 b) R 1 ; 0
c) R 0 ;
1
d) 1 ; 1 R
2
e) 0 ; 1 R
2
x
Sen7x
2Senx

53. Hallar el valor de :
E f
máx
f
mín
Si : f(x) = 2Cosx (Cosx - Senx) - 1
x
2
;
5
8
a) 2 2 b) 1 c) 2
d) 2 2 e) 1
54. Hallar los valores x en el intervalo
cuales existe f, si :
0 ; para los
a)
c)
e)
3
3
3
;
;
;
2
3
2
3
5
6
f(
x)
1
b)
d)
55. Señale : Rf Rg , si :
f(
x)
g(
x)
Sen Senx
Cos Senx
Senx
6
6
3Cosx
3Cosx
;
;
1
5
6
5
6
a) [Sen2 ; 1] b) [ 1 ; Sen2]
c) [Cos2 ; 1] d) [ 1 ; Cos2]
e) [Cos2 ; Sen2]
2
2Cos
x
56. Determine el rango de la función f definida por:
f(x)=|Senx|+|Cosx|.
a) [ 0;
2]
b) [
1
; 2]
c)
2
[ 1;
2]
d) [ 0;
1]
e) [
1
; 1]
2
57. Dada la función f definida por:
f(x)=Sen2x+|Senx+Cosx|
Hallar: f máx + f mín
a) 2 b) 2 2 c)
d) 3 e) 2(
1 2)
58. Determinar el periodo de:
f(
x)
Sen
x
2
3 2
2
Sen
x
3
a) 12 b) 18 c) 24
d) 48 e) 52
Sen
x
4
59. Si f es una función definida por:
f ( x)
Senx Cosx Tanx Cotx ; halle el dominio de
dicha función, k Z .
a) R b) [ 1;
1]
c) R { k / k Z}
2
d) R { 2k
/ k Z}
e) [ 0;
1]
60. Dada la función :
g(x) = Senx (Cosx + |Cosx|)
Señale su gráfico.
a)
b)
y
y
y
c)
x
d)
e)
y
y
x
x
x
x

Claves
Claves
b
c
d
b
c
b
d
c
b
b
b
e
e
a
d
b
a
a
c
b
a
b
a
c
d
d
c
e
b
e
d
e
e
d
b
d
e
b
a
b
a
e
d
b
c
d
e
d
a
c
d
b
e
d
c
c
b
c
c
b
01.
02.
03.
04.
05.
06.
07.
08.
09.
10.
11.
12.
13.
14.
15.
16.
17.
18.
19.
20.
21.
22.
23.
24.
25.
26.
27.
28.
29.
30.
31.
32.
33.
34.
35.
36.
37.
38.
39.
40.
41.
42.
43.
44.
45.
46.
47.
48.
49.
50.
51.
52.
53.
54.
55.
56.
57.
58.
59.
60.

Capítulo
14
FUNCIONES TRIGONOMÉTRICAS
INVERSAS
OBJETIVO
El objetivo del presente capítulo es analizar las funciones inversas de las funciones trigonométricas básicas; así como
familiarizarnos con las notaciones ArcSenx, ArcCosx, ArcTanx, etc; de modo que las interpretemos y operacionalicemos
correctamente según las propiedades que se darán convenientemente.
INTRODUCCIÓN
Según el análisis de funciones; la condición suficiente para que una función posea inversa, es que debe ser inyectiva :
f
y
x
y
g
f no es inyectiva g no es inyectiva
h si es inyectiva
Las funciones trigonométricas; debido a su carácter periódico no son inyectivas :
1
y
2
0
2
1
y=Senx
3 2
x
x
y
0
2 2
y
h
y=Tanx
Según este comentario, las funciones trigonométricas no poseen inversa. Sin embargo; es posible redefinir la función
trigonométrica, restringiendo su dominio (sin alterar su rango), a un intervalo donde sea inyectiva y en consecuencia se
pueda obtener su inversa.
OBTENCIÓN Y ANÁLISIS DE LAS FUNCIONES TRIGONOMÉTRICAS INVERSAS
I. F.T. SENO INVERSO O ARCO SENO
De la función : y = Senx
Tomamos el dominio :
El rango no cambia : 1 ; 1
Luego para hallar la inversa; hacemos en :
y Senx
2
;
2
x Seny
Esto es : "y es un ángulo arco o número cuyo Seno vale x".
Lo cual se denotará : y = ArcSenx
Finalmente, como el dominio y rango se intercambian con el de la función original; tendremos :
3 2
x
x

y
f(
x)
Dom :
Rang :
f
Senx
2
;
1 ; 1
2
y
f * ( x)
Dom *
Rang *
:
:
f *
ArcSenx
1 ; 1
;
2 2
Cumpliéndose : ArcSen( x) = ArcSenx
II. F.T. COSENO INVERSO O ARCO COSENO
De la función : y = Cosx
Tomamos el dominio : 0 ;
Sin cambiar el rango : 1 ; 1
Luego para hallar la inversa procedemos igual que en el caso del "ArcSenx"; obteniéndose :
y
f(
x)
Dom :
Rang :
f
Cosx
0
;
1 ;
1
y
f * ( x)
Dom *
Rang *
:
:
f *
ArcCosx
1 ; 1
Cumpliéndose : ArcCos( x) = ArcCosx
III. F.T. TANGENTE INVERSO O ARCO TANGENTE
De la función : y = Tanx,
tomamos el dominio :
sin cambiar el rango : ;
2
;
2
0
;
Luego, para hallar la inversa de la función Tangente, procedemos igual que en los casos anteriores, obteniéndose :
y
f(
x)
Dom :
Rang :
f
Tanx
2
;
;
2
y
f * ( x)
Dom *
Rang *
:
:
f *
ArcTanx
Cumpliéndose : ArcTan( x) = ArcTanx
IV. F.T. COTANGENTE INVERSA O ARCO COTANGENTE
y
f(
x)
Dom :
Rang :
f
Cotx
0
;
;
y
f * ( x)
Dom *
Rang *
:
:
f *
0
2
;
;
2
ArcCotx
;
;

Cumpliéndose : ArcCot( x) = ArcCotx
V. F.T. SECANTE INVERSA O ARCO SECANTE
y
f(
x)
Dom : 0 ;
Rang :
f
Secx
;
1
2
1 ;
y
f * ( x)
Dom *
Rang *
:
: 0 ;
Cumpliéndose : ArcSec( x) = ArcSecx
f *
ArcSecx
;
1
2
1 ;
VI. F.T. COSECANTE INVERSA O ARCO COSECANTE
y
f(
x)
Dom :
Rang :
f
Cscx
PROPIEDADES
2
;
2
; 1
{ 0}
1 ;
y
f * ( x)
Dom *
Rang *
1 . F.
T.
Arc F.T. (n) n ; n Dom(Arc F.T.)
Esto es :
Por ejemplo :
Sen
Sen(
ArcSen(
n))
Cos(
ArcCos(
n))
Tan(
ArcTan(
n))
Cot(
ArcCot(
n))
Sec(
ArcSec(
n))
Csc(
ArcCsc(
n))
ArcSen
1
3
Tan(ArcTan4) = 4
1
3
n ,
n ,
n ,
n ,
n ,
n ,
n
n
:
:
n 1 ; 1
n 1 ; 1
n R
n R
2 . Arc F.
T.
F.T. ( ) ; Rang(Arc F.T.)
Esto es :
ArcSen(
Sen
ArcCos(
Cos
ArcTan(
Tan
ArcCot(
Cot
ArcSec(
Sec
Csc(
ArcCsc
)
)
)
)
)
)
,
,
,
,
,
,
;
2
0 ;
;
2
0 ;
0 ;
2
;
2
2
2
2
;
;
{ 0}
f *
ArcCscx
2
1
1
;
;
1
2
1 ;
1 ;
1 ;
{ 0}

3 .
4 .
5 .
Por ejemplo :
ArcSen Sen ; pues :
5 5
ArcCos(Cos1) = 1 ; pues : 0 1
ArcTan ( Tan2)
2 ; pues 2
2
2
5
;
2
2
En este caso, se le busca un equivalente a "Tan2" en el intervalo correspondiente al rango del ArcTan, asi :
MA' = NA = 2; entonces : AN = 2
Note que : Tan2 = Tan(2 ) luego :
ArcTan(Tan2) = ArcTan[Tan(2 )]
ArcTan(Tan2) = 2
ya que :
ArcTanx
ArcSecx
2
2
ArcSenx ArcCosx ; x
2
ArcTanx
ArcCotx
ArcCscx
ArcTany
2
2
2
;
;
x
x
R
x y
ArcTan
1 xy
1 ; 1
;
n
1
1 ;
Si : xy 1
; n
Si : xy 1 ,
x
0 ; n
Si : xy 1 , x 0 ;
n
Si : xy 1 ; n
0
x y
ArcTanx ArcTany ArcTan n Si : xy 1,
x 0 ; n 1
1 xy
Si : xy 1,
x 0 ; n 1
0
1
1

01. Calcule : E
5
a)
12
d) 8
02. Calcule:
1
a)
2
d)
2 5
5
E
ArcSen
7
b)
12
e)
Sen
2
b)
3
5
e)
10
03. Halle el valor de:
2
a)
5
12
d)
13
3
b)
5
15
e)
8
3
2
ArcSec
Cos2
ArcCos
c) 9
5
2
5
c)
5
ArcTan
2
3
5
c)
13
04. Halle "x", si : 4ArcSenx = ArcCosx
1
a)
2
d)
5 1
4
05. Resolver :
1
b)
4
e)
ArcTan
5 1
4
x
x
2
1
3
c)
2
a) 1 b) 2 c) 0
d) 1 e) 2
ArcSec
06. Si : ArcCosy ArcSenx
2
,
3
calcule: M = ArcSeny + ArcCosx
a) 2
d) 5
07. La suma de :
b) 3
e) 6
ArcSen
3
,
2
ArcSec
2
es :
3
c) 4
2
2
x
2
ArcSen
2
, ArcTan0 y
2
EJERCICIOS PROPUESTOS
3
a) 0 b)
4
d)
3
2
2
2
2
3
3
c)
2
4
e)
3
2
2
08. Reducir: M Sec ( ArcTan3)
Csc ( ArcCot4)
a) 7 b) 13 c) 15
d) 27 e) 12
09. El resultado de :
ArcCos
3 1
ArcSen
3
2 2
2
es :
a) 120º b) 150º c) 60º
d) 30º e) 240º
10. Calcular : Sec(Arc Tanb)
a) b
1
b) 2b
c) No se puede determinar
d)
b e) 2
1 b
2
11.
Determinar el valor de la expresión :
a)
c)
e)
P
4 5 1
5 10
5 5 1
6 10
6 6 1
5 10
Cos
ArcSen
b)
d)
1
5
5 5 1
6 10
6 6 1
5 10
ArcTan
12. La expresión trigonométrica ArcCosu=z significa
Cosz = u.
Suponiendo : z [ 0 ; ] .
Hallar :
1
a)
2
d)
2 3
3
2Sen
ArcCos
1
2
3
b)
4
3
e)
3
c) 3
1
3

13. Dada la ecuación: ArcTan(x+1) ArcTan(x 1)=ArcTan1
Indicar la suma de las soluciones
a) 2 b) 1 c) 0
d) 1 e) 2
14. Si: ArcTan 3
3
ArcTan
2
ArcTan3
,
entonces :
a) 9 3 2
2
b)
1
3
c) 9 3 2
2
d)
e)
2
3
2
3
ó
ó
1
3
1
3
15. Si : Tan(ArcTan2x) + Cot(ArcCotx) = 6,
calcule :
K
Tan
2
a) 2 b)
2
d)
2 3
3
3
e)
2
16. Dada la función :
halle :
Dom
g
ArcCos
x
x 1
2
c)
4
a) 2 ; 3 b) 1
2
; 2
c) 1 ;
1
2
d) 1 ; 2
e) 2 ; 1
17. Dada la función :
halle :
a)
c)
e)
Dom
h
g ( x)
2
ArcSen
2x
1
,
3 3
h ( x)
5
ArcCos
6x
5
,
6 7
1 ;
4
1
b) ; 2
3
3
2 ;
1
5
d) ; 2
3
6
1
3
;
5
6
18. Dada la función :
halle :
Rango
g
g ( x)
2ArcSen
x
,
2
a) ; 3 b) ;
c) 2 ; 0 d)
e) 0 ; 2
19. Dada la función :
halle :
a)
c)
e)
Rango
h
2
0 ;
3
b) ;
4
4
5
8
5
4
;
;
7
8
3
2
;
3
2
h ( x)
1
ArcCos4x
3
,
4
4
d)
20. Graficar : y 4ArcSen(
x 1)
a)
c)
e)
y
y
21. Grafique la función :
a)
c)
y
y
y
x
x
x
x
x
y
b)
d)
b)
d)
y
y
2
;
2ArcCosx
y
y
4
x
x
x
x

22. Calcule :
ArcSen Sen
6
7
ArcSen Sen
6
a) 0 b)
d) 3
e) 2
6
ArcSen Sen
5
6
c) 6
23. Calcule: ArcCos(
Cos2)
ArcCos(
Cos4)
a) 2 1 b) 2 1
c) 2( 1)
d) 2(
1)
e) 2(
2)
24. Calcular el valor de:
x
ArcTan
2
2
a) 22º30' b) 45º c) 67º30'
d) 30º e) 60º
1
1
ArcTan
25. Hallar x, sabiendo que: ArcCos
8
ArcSenx
3
8
a) 30º b)
9
1
d)
3
e) 15º
1
c)
2
26. El valor o valores que verifican :
Son :
a)
c)
e)
5
4
7
4
5
4
y
y
27. Hallar : x
y
Cos(
ArcSenx)
7
4
7
4
5
4
2ArcCot2
4
a) 0 b)
5
7
d)
25
25
e)
24
Sen(
ArcCosx)
7
b) Sólo
4
d)
ArcCos
7
4
3
5
24
c)
5
3
2
ArcCscx
1
2
28. Señale el rango de la función :
y = f(x) = ArcSenx+ArcCosx+ArcTanx
a)
c)
2
2
e) 0 ;
29. Calcule :
a) 4
5
d)
6
;
;
3
2
3
2
b)
d)
ArcSen
15
17
b) 2
e)
30. Al resolver la ecuación :
Tan
ArcSen
tenemos :
a)
c)
e)
x
31. Si :
1
2
x
4
4
;
;
3
4
3
4
ArcSen
3
5
3
c)
4
Sen(
ArcTan2)
x
5
b) x no existe.
3
5
x d) x = 1
5
33
65
ArcSen
0 ,
2
ArcSen ArcSen
1
1
1 2
,
el valor de " " es :
a) 1 ; 0 b)
2
3
c) 0 1 d) 1 ; 2
e) 1
32. Evaluar la expresión :
Sen 3ArcTan
1
11
2ArcTan
27
4
a) 0 b) 1 c) 3
d) 11 e) 27
11
33. Calcular el valor de la siguiente expresión:
Sen
2ArcCot(
4)
ArcTan
5
12
13
85

9
a)
100
19
b)
200
1
d) 0 e)
10
21
c)
221
34. Si 0 x 1 , entonces, podemos afirmar que
2
ArcCos(
2x
1)
es igual a :
a) Arc Cosx b) Arc Senx
c) 2Arc Senx d) 2 Arc Cosx
e) Arc Cos2x
35. Resolver la ecuación:
a) x
1 3
b) x
2 7
c) 1 d)
e)
x
1
3
3
7
ArcSen2x
x
1
2
1
3
3
7
3
7
ArcSenx
36. Si : x ArcCot Sec ArcTan Sec y Cosx > 0, el
valor de Senx es :
a) Tan
2
2
c)
Tan
2
2
e) Cot
2
2
b)
d)
Cot 2
2
Tan
37. Calcular el valor de "m", para que se cumpla la siguiente
igualdad: Sen(ArcTanm) = Tan(ArcSenm)
a) 1 b) 0 c) 1
d) 2 e) 2
38. Resolver:
ArcCos x
1
2
ArcCosx
a) 0 b) 1 ; 0 ; 1
c) 0 ; 1
e)
1
4
; 0 ;
1
4
39. Si :
halle :
a b c ,
ArcTan
a
bc
d)
ArcTan
0 ;
b
ac
1
4
2
ArcTan
ArcCos x
c
ab
1
2
3
3
2
a) 0 b) 4
2
d)
3
40. Reduzca:
e)
2ArcTanx
Para : x ; 1
c) 6
a) b) 2ArcTanx
c) 4ArcTanx d)
e) 0
ArcSen
2x
2
1 x
41. Señale el número de raíces de la ecuación:
2
x
a) 1 b) 2 c) 3
d) 4 e) Ninguna
2
42. Acerca de la función:
Podemos afirmar que :
I. Dom : 0 ; 2 2
f
II.
Ran : 0 ;
f 2
6
f(
x)
x
2ArcCos
ArcSen 1
III. "f" es decreciente x 0 ; 1
Luego, es correcto :
a) Sólo I
b) Sólo II
c) Sólo III
e) II y III
d) I y II
x
2
3 2
x
43. Si : x
3
;
1
, determine el rango de la
2 2
función:
g(
x)
3
6ArcCosx
1
a) 1 ; 2 b) ; 1
2
c)
e)
3
7
3
5
; 3
;
3
2
44. Calcular el valor de :
a)
5
4
3
Cos
d)
b)
2
1
2
;
3
2
1
ArcSen
1
2 4
5
4
3
2

c)
e)
5
4
3
5
4
2
d)
5
4
45. Señale el dominio de la función :
h(
x)
1
4
ArcCos
a) 2 ; 2 b) 1 ; 1
c) 1 ; 2 d) 2 ; 1
e) 0 ; 3
2
3x
46. Obtenga el valor de la expresión :
A
ArcSen(
x
ArcCot
a) 0 b)
d)
1
3
47. Reduzca :
a)
c)
e)
J
e)
2)
2x
ArcCosx
2
3
3
5
1
ArcSen
2
3
ArcSen
1
b)
6
ArcSen
1
d)
4
ArcSen
1
3
ArcTan
2
ArcCsc x
5
c)
3
| x |
4
x
1
2
ArcSen
2 15
12
ArcSen
2
5
ArcSen
2
7
48. Halle el valor de la expresión :
N
3
Sen
7 6
a)
18
d)
5 2
9
4
ArcCos
1
3
3
Cos
5 6
b)
18
e)
7 2
4
4
ArcSen
49. Si: ArcSenx + ArcSeny + ArcSenz = ,
calcule:
H
2
1 x
yz
2
1 y
zx
a) 1 b) 2 c) 2
d) 4 e) 4
2
3
c)
2
1 z
xy
5
7 3
9
50. Calcule :
a) 10
d) 40
1
ArcTan
2
3
2
1
3
b) 18
e) 72
51. Resolver :
ArcTan
x
1 x
a) 3
d) 4
3
5
4
5
b) 4
3
4
e) 3 2
1
ArcTan
3
c) 36
ArcTan
c) 4 6
2
3
2 1
3
1 x
x
52. Al resolver la ecuación : x 3x
1 0
3
,
se obtiene como raíces :
x ,
1
Calcule el valor de :
3
ArcSen
k 1
a)
9
13
d)
9
b) 10
e)
26
9
x ,
2
1
x
2 k
c) 18
x
3
53. Del gráfico mostrado, halle :
a + 3b c
y
y=a+b.ArcCos(cx)
a) 12
d) 3
y=ArcSenx
b)
6
7
e)
12
54. Se define la función :
f(
x)
2
ArcTan x
2
2
c) 4
4ArcTanx
Halle el dominio de dicha función :
x
5
6
3

a) ; Tan1 b) Tan1
;
c) R d) Tan1
; Tan1
e) 0 ; Tan1
55. Qué valor de "x" maximiza :
a)
c)
3 1
2
6
4
6
e)
3
2
y
f(
x)
56. Del gráfico, calcular :
1
a)
2
1
b)
4
3
d) 4 e)
4
K
5
( ArcSenx)
( ArcCosx)
b)
d)
3 1
2
6
4
Tan
y
2
Tan
y=ArcCosx
x
y=2ArcSenx
c) 2
57. Dada la función "f" definida por :
halle :
a)
d) 4
4
58. Calcule :
a) 10
d) 18
f ( x)
ArcSenx ArcCotx ,
b)
e) 2
M
b) 9
e) 20
2
fmáx fmín
2
ArcTan
c) 0
3
Csc10º
c) 5
1
59. Graficar :
a)
b)
c)
60. Si :
1
1
Tan(
2ArcTan
y
2
2
y
2
y
2
f(
x)
1
y
1
Cos2
mCsc p
n
Calcule : W = m + n p
ArcSen
x
x
x
) Sen(
ArcCsc
a) 1 b) 2 c) 3
d) 4 e) 5
2x
2
1 x
Sec2
)

Claves
Claves
b
c
c
d
b
b
b
d
a
e
e
c
c
b
b
d
b
c
b
c
b
c
d
b
d
c
e
b
b
a
a
a
c
d
a
a
b
a
e
d
a
c
b
c
c
d
c
a
b
c
b
c
b
a
d
a
b
b
a
c
01.
02.
03.
04.
05.
06.
07.
08.
09.
10.
11.
12.
13.
14.
15.
16.
17.
18.
19.
20.
21.
22.
23.
24.
25.
26.
27.
28.
29.
30.
31.
32.
33.
34.
35.
36.
37.
38.
39.
40.
41.
42.
43.
44.
45.
46.
47.
48.
49.
50.
51.
52.
53.
54.
55.
56.
57.
58.
59.
60.

Capítulo
15
ECUACIONES EINECUACIONES
TRIGONOMÉTRICAS
ECUACIONES TRIGONOMÉTRICAS
Son igualdades condicionales donde la variable (x) o arcos de la forma (ax + b) se encuentran afectados de algún operador
trigonométrico como el seno, coseno, etc.
Es de la forma : F.T. (ax + b) = N ............... (*)
Donde el valor principal (Vp) es el valor del ángulo o arco (ax + b) definido en el "rango" de la función trigonométrica
inversa.
De (*) : Vp = Arc F.T. (N)
Además N debe pertenecer al dominio de la función trigonométrica; a y b son constantes reales con
Ejemplo : De las ecuaciones trigonométricas elementales, con sus respectivos valores principales :
a 0 .
*
*
*
Sen3x
Cos
Tan
2x
3x
5
3
2
4
8
Vp
1
2
1
ArcSen
Vp
Vp
3
2
ArcCos
ArcTan(
3
1)
1
2
2
3
4
EXPRESIONES GENERALES DE TODOS LOS ARCOS QUE TIENEN LA MISMA FUNCIÓN
TRIGONOMÉTRICA
ECUACIÓN SOLUCIÓN
Si : Senx
N
x
K
K
( 1) Vp
Obs : Vp = ArcSen(N)
ECUACIÓN SOLUCIÓN
Si : Cosx
N
x
2K
Vp
Obs : Vp = ArcCos(N)
;
;
k
K
Z
Z

ECUACIÓN SOLUCIÓN
Si : Tanx
N
x
K
Vp
Obs : Vp = ArcTan(N)
INECUACIONES TRIGONOMÉTRICAS
Inecuación Trigonométrica : Es una desigualdad condicional que involucra funciones trigonométricas por lo menos
una.
Ejemplos :
* Sen2x > Cosx
* Tan2x + Cot2x > Cscx
*
*
3
Sen xCosx
Sen2x
1
3
3
SenxCos x
1
4
Inecuación Trigonométrica Elemental : Una inecuación trigonométrica se llamará elemental, cuando es de la forma :
Ejemplos :
*
*
Senx
Cos2x
1
2
* Tan3x
1
3
2
F.
T .(Kx .( Kx
Resolución de una Inecuación Trigonométrica Elemental :
Se estila seguir dos métodos :
Resolver :
Senx
1
2
)
a , x : incógnita
;
K
Z

Método I :
1
En la circunferencia trigonométrica, ubicamos todos los arcos "x" cuyos senos sean mayores que , así :
2
2 1
5
6 6
y
x 2+y 2=1
Método II :
Graficamos en un mismo sistema coordenado las funciones :
f(
x)
Senx
Senx
1
2 6
x
5
6
El conjunto solución general será :
Los puntos de intersección en un periodo del Senx : osea en 0 ; 2 , se obtienen con :
1
2 1
1
y
6
f ff(
f
(
x xx)
x)
)
x
5 6
g(
x)
6
Senx
x
6
x
g(x)
1
2
5
6
2n
1
2
6
x
2n
2
5
6
;
g(
x)
5
6
x
2n
1
2
2n
f(x)=Senx
;
n
; n
Z
Z

01. Sume las dos primeras soluciones positivas de:
Sen2x
1
2
a) 180º b) 360º c) 90º
d) 270º e) 135º
02. Sume las dos primeras soluciones positivas de :
Cos3x
1
2
a) 120º b) 240º c) 300º
d) 260º e) 270º
03. Sume las dos primeras soluciones positivas de :
Tan(
2x
30º
)
a) 170º b) 180º c) 200º
d) 210º e) 150º
04. Si : x y
1
x
2
son los dos primeros valores positivos de
"x" que verifican :
calcule : Sen(
x x ) ,
2 1
si : x
1
3
a)
2
d)
1
2
x
2
1
b)
2
e)
3
2
2Sen
x Cosx 1,
3
2
c) 1
05. Resolver :
(Sen4x+Cos4x)(Senx+Cosx)=1+Sen5x
Indique la suma de los tres primeros valores positivos
de "x"
a) 2 b) 3 c)
7
d)
3
e) 4
06. Sume las tres primeras soluciones positivas de la
ecuación :
Sen5x
Sen3x
3(
Cos5x
a) 135º b) 180º c) 165º
d) 160º e) 210º
EJERCICIOS PROPUESTOS
Cos3x)
07. Señale la suma de las dos menores soluciones positivas
de la ecuación :
2
Sen x
4
Sen x
4
Cos x
1
a) 90º b) 180º c) 270º
d) 225º e) 135º
08. Resolver :
1
2
Cos x
1
2
Sen x
2
2
Tan x
1
2
Cot x
Luego, señale la suma de las dos primeras soluciones
positivas.
a) 90º b) 135º c) 180º
d) 225º e) 270º
09. Al resolver la ecuación :
Cos4x
Cos2x
Sen4x
Sen2x
2Cos
Luego, señale la menor solución positiva.
a) 4
d) 8
10. Resolver :
b) 6
e) 12
c) 3
SenxCosy
4
........... (1)
5
SenyCosx
1
........... (2)
5
Para :
x
,
y
0 ; 90º
a) x = 63º30' ; y = 26º30'
b) x = 53º ; y = 37º
c) x = 71º30' ; y = 18º30'
d) x = 67º30º ; y = 22º30'
e) x = 60º ; y = 30º
11. Resolver :
a)
c)
e)
1
2
1
2
;
2
2
12. Resolver :
3
2
Cos(
2ArcCosx)
b)
d)
3
2
1 ;
3
2
1
2
Sen 2x
Cos ; n Z
9
1

a)
c)
e)
5
n ( 1)
b)
18
n
n
( 1)
7
18
n n
( 1)
2
13. Resolver :
5
18
d)
n n
( 1)
2
2n
7
36
n
( 1)
9
2Cos5x . Cosx - Cos6x = 1 ; n Z
a) 2n b) 4n
c) n d)
e)
n
4
n
2
14. Resolver : Secx = 6Senx ; n Z
a)
b)
c)
d)
e)
n
n
2
n
n
2
n
2
n
( 1)
ArcSen
1
2 6
n
( 1)
ArcSen
1
2 6
n
( 1)
ArcSen
1
2 3
n
( 1)
ArcSen
1
2 3
n
( 1)
ArcSen
2
2 3
15. Resolver en el intervalo de 0 ; 2 la inecuación :
a)
c)
e)
6
6
3
;
;
;
5
6
5
6
2
3
b)
d)
Senx
16. Resolver en el intervalo de 0 ; 2 la inecuación :
1
2
6
3
;
;
1
2
5
6
2
3
Cosx
1
2
a)
b)
c)
d)
e)
3
6
3
6
6
;
;
;
;
;
2
3
5
6
2
3
5
6
2
3
4
3
7
6
4
3
7
6
7
6
;
;
;
5
3
11
6
5
3
;
11
6
;
17. Resolver en el intervalo de 0 ; la inecuación :
a)
c)
e)
4
4
4
;
;
;
2
3
4
18. Resolver :
Para :
x 0 ;
a)
2
;
c)
3
;
4
e)
4
3
4
3
4
19. Resolver :
;
2
3
Sen
2
Tan x
2
b)
5
3
0 ;
d) ;
2
Tanx
4
2Cosx
1
2Senx
Cosx
b) ;
4
d)
x
Cos
x
2 2
en el intervalo de 0 ; 2
a)
c)
6
6
;
;
5
6
5
6
e) 0 ;
5
;
6 6
0 ;
b)
d)
4
7
0
0
x 3
Sen Cos
x
2 2
3
3
;
;
2
3
2
3
1
4

20. Resolver en 0 ; 2
a)
6
;
2
7
c) ; 2
6
e) a c
Sen2x > Cosx
b)
5
6
d) a b
21. Dada la ecuación :
Cosx + Cos2x + Cos3x = 0,
hallar la suma de todas las soluciones de dicha
ecuación, si estas soluciones están comprendidas entre
0 y 2 (radianes).
a) b) 2 c) 4
d) 3 e) 6
22. Al resolver el sistema :
2Senx
6Senx
3Tany
Tany
2
4
3
3
,
se obtiene que la solución en el primer cuadrante es :
a) x = 45º , y = 45º
b) x = 60º , y = 30º
c) x = 30º , y = 60º
d) x = 60º , y = 45º
e) x = 60º , y = 60º
23. Al resolver la ecuación :
Sen2x
2
Cos x TanxCscx ,
calcular la diferencia entre dos de dichas soluciones :
2
a)
3
2
d)
15
b) 6
3
e)
4
;
3
2
c) 12
24. Resolver la siguiente ecuación :
a)
c)
e)
2
2
2
,
,
,
2SenxCos2x
12
6
12
,
,
,
8
12
5
12
b)
d)
2Cos2x
2
2
,
,
6
6
,
,
4
5
6
Senx
25. Hallar "x" en :
Sen40º Senx = Cos40º Cosx - 2Cos20º Cosx
a) 130º b) 150º c) 60º
d) 135º e) 120º
1
0
2
26. Al resolver la ecuación 3Tan
1
0 2 , la suma de todas sus soluciones es :
a) 2 b) 3 c) 4
d) 5
e) 6
donde
27. La suma de las soluciones, en el intervalo [0º ; 360º]
de la ecuación :
2Sen2x Senx Cosx es :
a) 450º b) 495º c) 600º
d) 945º e) 1170º
28. La afirmación que cumple con la siguiente inecuación:
a)
x
Arc Sen
b) Cosx
2
6
5
c)
Senx
2
3
3Senx
1
5
d) x Arc Sen
1
2
5
e)
29. Si
x y
1
x
9
4
2Cosx
x son dos soluciones de la ecuación : 5Cosx
2
4Senx = 4,
entonces el valor de :
Senx
Senx Senx Senx es :
1 2 1 2
a) 0 b) 1 c) 1
d) 1 2 e)
1
2
2
30. Dada la función f cuya regla de correspondencia es :
f(x) = Cosx Sen2x
En la que x varía : x 2
El número de intersecciones de la función y = f(x) con
el eje de abscisas es :
a) 3 b) 4 c)5
d) 6 e) 7
31. Resolver la desigualdad :
Sen2x > Senx , 0 x
a)
c)
0 ;
0 ;
3
3
b)
d)
0 ;
0 ;
3
3
3

e) 0 ;
32. Calcular la suma de las soluciones de la ecuación
trigonométrica, si
a) 2
d) 3
3Cosx
b)
e)
33. Resolver la ecuación :
x
2Sen
2
2
4
;
c)
2
x
2
3
Cos
Tan2x
Cotx
2
8Cos
x
NOTA : K es un número entero.
a)
b)
c)
d)
e)
K k
( 1)
4 3
K k
( 1)
4 6
K k
( 1)
4 12
K k
( 1)
4 24
K k
( 1)
4 48
34. Hallar el menor ángulo en el intervalo
que satisface la ecuación :
a)
10
3
2
2Tan
x
2
b)
3
8
d) 0 e)
3
3Secx
4
c)
3
0
4
x
2
7
3
;
11
3
35. Determinar la suma de todas las soluciones de la
ecuación :
Sen
1
x
2
1
Senx
Que se encuentran en el intervalo [ 0 ; ]
a)
2
b)
4
d) 0 e)
c) 3
1
36. Resolver la ecuación :
Sen2x + 5Senx + 5Cosx + 1 = 0
a) k ; k Z
4
b) 2k
; k Z
4
c)
3
2k
; k Z
4
d) k ; k Z
4
e)
3
k ; k Z
4
37. Resolver la ecuación :
Sen4x + 3Sen2x = Tanx
a)
k
; k Z
3
b) 2k
; k Z
c) k ; k Z
3
d)
k
; k Z
6
e)
k
; k Z
4
38. Resolver e indicar el número de soluciones
en 0 ; 2
de la ecuación :
Cosx = (2 Tanx) (1 + Senx)
a) 2 b) 3
c) 4 d) 1
e) No existen soluciones.
39. Si k es un número entero, las soluciones de la ecuación:
a)
c) k
e)
2Sen
x
k b)
4
2k
k
( 1)
3
6
d)
4
k
k
2
SenxSec x son :
4
k
( 1)
6
40. El ángulo en grados, que satisface la ecuación :
3
2Cos
2
Pertenece al intervalo :
a) 180º
; 240º
1
Cos
6

) 120º
; 135º
c) 300º
; 300º
d) 90º
; 120º
e) 240º
; 270º
41. El número de elementos del conjunto :
F
es :
x
[ 0 ; 2
] / Cos2xSecx
a) 1 b) 2 c) 3
d) 4 e) 5
Secx
42. Resolver la siguiente ecuación trigonométrica :
a)
1
( 2k
1)
2
c)
1
( 2k
1)
4
e)
1
( 4k
3)
2
Cot
x
2
Senx
b)
1
( 2k
1)
3
d)
1
( 4k
1)
2
1
Cotx
43. Indique una solución general para la ecuación :
4Cosx Cos2x Cos3x = 1
a)
b)
c)
d)
e)
k ; k Z
4
k ; k Z
2
k ; k Z
3
k ; k Z
6
k ; k Z
8
44. Sea : 0 x ; 0 y
2 4
Entonces el intervalo en el que x satisface la igualdad :
Tany = 2Senx es :
a) 0 x
b) 0
6
c) 0 x
d) 0
6
x
x
6
6
0
e) 0
x
4
45. En el intervalo 0 ; 2 , para qué valores de , se
cumple la siguiente desigualdad:
a)
0 ;
2
3
2
;
Sec
7
4
b) 0 ;
3
; 2
2 2
3
c) ; 2
2
d)
2
;
3
2
e) ;
3
; 2
2 2
Tan
46. Para qué valores de x 0 ; , se cumple:
Cos 2
x
2
a) 0 ;
b)
c)
0 ;
d)
2
2
e) ;
3
0 ;
0 ;
Cos
3
2
3
2x
3
47. Calcule la mayor solución negativa de la ecuación :
Tanx
a)
d)
9
5
9
48. Resuelva :
( Tan2x
k
a)
c)
e)
Z
k
4
k
k
8
Tan x
b)
e)
2
Cot2x)
8
4
8
Tan x
18
2
9
17
36
| Tan2x
b)
d)
k
2
k
Tan x
9
c)
4
9
Cot2x
|
8
16
0
6
6

49. Resolver :
4
Cos
9x
2
4
Cos
3x
2
k Z
a)
c)
e)
( 4k
1)
b)
2
4
Sen
k
6
( 2k
1)
d)
k
2 12
( 4k
1)
12
9x
2
4
Sen
3x
2
50. Halle el menor valor positivo que resuelve la ecuación
trigonométrica :
a) 15
d) 4
Cos6x
b) 12
e) 6
51. Resuelva la ecuación :
3
2
4Cos
2x
c) 5
1
3
2
Cos x
28
| Cosx |
9
e indique la suma de soluciones en el intervalo de
0 ; 2
a) 5 b) 4 c) 6
9
d)
2
52. Si :
x 1
calcule "n"
7
e)
2
Sen
14
f(
x)
es una raíz de :
8x
3
4x
a) 1 b) 2 c) 7
d) 1 e) 7
53. Resolver la ecuación :
n
a)
c)
Z
e) 2n
2Tan3x
n b)
3
3Tan2x
n
2n d) n
6
2
4x
n ,
2
Tan 2xTan3x
6
54. Resolver :
k
a)
c)
e)
Z
k
6
2k
3
k
2
24
12
24
Tan5x Tanx = Tan2x Tan3x
b)
d)
k
3
2k
3
55. Si : x
1
x son las dos menores soluciones positivas
2
de la ecuación :
3
2
5Tan
x
Tal que : x
1
x ,
2
halle :
x
2
x
1
a) 3 b) 6 c) 4
d) 8 e) 5
56. Resolver :
k
a)
b)
c)
d)
e)
Z
2
k
2
k
k
k
2k
57. Resolver :
a)
b)
c)
n
n
n
2
2
Sen x
ArcCos
1
3
ArcCos
2
3
k
( 1)
ArcSen
2
3
k
( 1)
ArcSen
1
3
ArcTan
1
3
18
9
2
2
Tan 5x(
5 3Tan
x)
3
Cos x
23
27
4
8Sen
x Cos4x
; n Z
ArcCos
3
4
1
ArcCos
3
2 4
ArcCos
3
4

d)
e)
n
2
n
4
1
ArcCos
3
2 4
1
ArcCos
3
2 4
58. Si el determinante de la matriz :
C
Es : 0,5Sen2x
Hallar "x" ( n Z )
a)
c)
n
2
n
e) a y c
n
( 1)
6
Senx
Sen2x
1
b)
n
d) a y b
Sen3x
Sen4x
1
n
( 1)
6
Sen5x
Sen6x
59. Resolver :
13(1 + Senx + Cosx) + Sen2x = 0
n
a)
Z
n
n
( 1)
4
1
b)
c)
d)
e)
n
n
n
n
60. Resuelva :
n
( 1)
4
n
( 1)
2
n
( 1)
4
n
( 1)
4
4
4
Sen
x
2
2
Sen
x
4
e indique como respuesta la suma de soluciones en
0 ; 8
a) 12 b) 16 c) 20
d) 15
e) 28
0

Claves
Claves
c
a
b
d
e
c
b
c
b
a
b
b
d
d
b
c
c
e
c
d
e
e
a
d
e
c
b
d
b
c
c
c
d
e
d
d
a
a
b
c
b
a
c
d
b
c
c
a
b
b
b
a
d
b
c
b
b
c
d
c
01.
02.
03.
04.
05.
06.
07.
08.
09.
10.
11.
12.
13.
14.
15.
16.
17.
18.
19.
20.
21.
22.
23.
24.
25.
26.
27.
28.
29.
30.
31.
32.
33.
34.
35.
36.
37.
38.
39.
40.
41.
42.
43.
44.
45.
46.
47.
48.
49.
50.
51.
52.
53.
54.
55.
56.
57.
58.
59.
60.

Capítulo
16
¿Qué es resolver un triángulo?
RESOLUCIÓN DE TRIÁNGULOS
OBLICUÁNGULOS
Dado el triángulo ABC, oblicuángulo; resolverlo significa determinar las medidas de sus elementos básicos; es decir, sus tres
lados (a, b y c) y sus tres ángulos (A, B y C); a partir de ciertos datos que definan el triángulo.
¿Cómo resolver un triángulo?
Una vez que reconocemos los datos del triángulo y verificamos que se encuentra definido; para resolverlo, se utilizarán
algunas propiedades geométricas, relaciones trigonométricas ya conocidas y otras propias del capítulo como las siguientes:
I. TEOREMA DE LOS SENOS :
"En todo triángulo, las medidas de sus lados son proporcionales a los senos de sus ángulos opuestos"
A
c
B
b
a
C
a
SenA
b
SenB
De donde :
aSenB = bSenA
bSenC = cSenB
cSenA = aSenC
Corolario :
"En todo triángulo, las medidas de sus lados son proporcionales a los senos de sus ángulos opuestos; siendo la
constante de proporcionalidad, el diámetro de la circunferencia circunscrita al triángulo".
II. TEOREMA DE LOS COSENOS :
A
c
B
b
a
R
C
a
SenA
b
SenB
R : Circunradio
De donde :
a = 2RSenA
b = 2RSenB
c = 2RSenC
c
SenC
c
SenC
2R

"En todo triángulo, el cuadrado de la longitud de uno de sus lados es igual a la suma de los cuadrados de las longitudes
de los otros dos lados, menos el doble del producto de los mismos multiplicados por el Coseno del ángulo formado por
ellos".
A
De donde podemos deducir fácilmente :
c
CosA
B
b
2
b
2
c
2bc
a
2
a
C
CosB
2
a
2
c
2ac
2
b
a 2 = b 2 + c2 2bc CosA
b 2 = a 2 + c2 2ac CosB
c 2 = a 2 + b2 2ab CosC
III. TEOREMA DE LAS PROYECCIONES :
"En todo triángulo, la longitud de un lado es igual a la suma de los productos de cada una de las otras dos longitudes con
el Coseno del ángulo que forman con el primer lado":
A
c
B
b
a
C
CosC
2
a
2
b
2ab
2
c
a = bCosC + cCosB
b = aCosC + cCosA
c = aCosB + bCosA
IV. TEOREMA DE LAS TANGENTES :
"En todo triángulo se cumple que la suma de longitudes de dos de sus lados, es a su diferencia; como la Tangente de la
semisuma de los ángulos opuestos a dichos lados, es a la Tangente de la semidiferencia de los mismos ángulos".
B
a
a
b
b
ALGUNAS LÍNEAS NOTABLES
Tan
A B
2
Tan
A B
2
A
c
b
b
c
c
Tan
Tan
b
a
B C
2
B C
2
C
c
c
a
a
Tan
C A
2
Tan
C A
2

RADIOS NOTABLES
r : inradio
r
A
m : Mediana relativa a “a”
a
A
m a
B C
M a
V : Bisectriz interior del “A”
A
A
2
4m
a
4m
2
b
2
4m
c
V A
2
b
2
a
2
a
2bc
b c
2
c
2
c
2
b
2bcCosA
2acCosB
V
B
2ac
a c
B
Cos
2
B D
VA C
V
C
2ab
a b
C
Cos
2
V’ : Bisectriz exterior del “A”
A
B C
r
B C
4Rsen
A
Sen
2
B
Sen
2
C
2
A
r b
r c
V’ A
4RSen
V' A
V' B
V' C
2abCosC
Cos
A
2
2bc
Sen
A
| b c | 2
2ac
B
Sen
| a c | 2
2ab
Sen
C
| a b|
2
r a : Exradio relativo al lado “a”
r 4RSen
A
Cos
B
Cos
C
a 2 2 2
4RSen
B
Cos
A
Cos
C
2 2 2
C
Cos
A
Cos
2 2
A
B
2
B
C
r a

01. En un triángulo ABC: Â 30º
; B 135º
ˆ Calcular : "c"
y a = 2.
a) 6 2
b)
c)
d)
6
2
6
2
6
4
e) 3 1
2
2
2
02. En un triángulo ABC : a = 3 ; b = 2
Ĉ 60º
.
Calcular : "c"
a) 3 2
b) 2 6
c) 6
d) 13
e) 7
03. En un triángulo ABC, se tiene que :
SenA
2
Halle el valor de :
25
a)
12
25
b)
7
13
c)
7
d) 5
12
e)
5
04. En un triángulo ABC:
J
a
3
¿Cuál es la medida de Ĉ ?
a) 60º
b) 30º
SenB
3
2
b
2
b
b
5
2
c
2
a
c
7
SenC
4
EJERCICIOS PROPUESTOS
c) 120º
d) 150º
e) 127º
05. En un triángulo ABC; simplificar :
a) TanA
b) CotA
c) TanB . TanC
d) TanC CotB
e) Tan A
2
J
2
a
2
a
2
c
2
b
2
b
2
c
06. En un triángulo ABC, se sabe que :
Calcular :
a) 0,
125
b) 0,
625
c) 0,25
d) 0,125
e) 0,625
Cos
B
2
2
a
2
c
2
b
1
ac
2
07. En un triángulo ABC, se cumple :
aCotA = bCotB = cCotC
¿Qué tipo de triángulo es?
a) Isósceles.
b) Equilátero.
c) Acutángulo.
d) Obtusángulo.
e) Rectángulo.
08. En el prisma rectangular mostrado, calcular: Sec
a)
5 2
3
2
3
4

)
c)
d)
e)
26 2
15
26 2
29
15 2
13
13 2
11
09. En un triángulo ABC, reducir :
a) R
b) 2R
c)
R
2
d) 4R
R
e)
4
Q
aCosB bCosA
SenC
10. En un triángulo ABC, reducir :
a) 1
b) 2
c)
1
2
d) 4
e)
1
4
Q
abCosC bcCosA caCosB
2
a
2
b
2
c
11. En un triángulo ABC, se cumple :
(a c) CosB = b (CosC CosA)
¿Qué tipo de triángulo es?
a) Acutángulo.
b) Rectángulo.
c) Equilátero.
d) Obtusángulo.
e) Isósceles.
12. En un triángulo ABC, simplificar :
(p : Semiperímetro)
Q
a) p
b) 2p
c) 3p
d) 4p
e) 8p
aSenB bSenA
SenA
cSenA aSenC
SenC
bSenC cSenB
SenB
13. En un triángulo ABC, reduzca :
G = (aCosC + cCosA) CosC + (aCosB +
bCosA) CosB
a) a
b) b
c) c
d) 0
e) a + b + c
14. En un triángulo ABC, reduzca la expresión
1
a)
2
b) 1
c) a
d) b + c
e) a
1
c
G
SenA
SenB
SenB
SenC
c
b
15. En un triángulo ABC, se tiene que :
2a = 7b
Halle el valor de :
m C 60º
a)
b)
c)
d)
e)
5 3
3
5 3
9
9 3
5
7 3
2
2 3
7
Tan
A B
2
a
c

16. En un triángulo ABC, se cumple :
Halle :
a) 7
7
b)
7
5
c)
2
5
d)
5
e)
5
7
Tan
A
2
2
a
3
bc
2
2
b
2
c
a bCosC
17. Si en un triángulo ABC; 3
b aCosC
Calcular : G
a) 1
b) 2
c) 4
1
d)
2
1
e)
4
Tan
C
2
Tan
A B
2
18. En un triángulo ABC :
Calcular :
a) 0,
2
b) 0,
3
c) 0,
4
d) 0,
5
e) 0,
6
Tan
C
2
2
a
2
b
2
c
1
ab
2
19. En el triángulo equilátero ABC; BP = 5AP AN = 2NC.
Calcular : Sec
A
P
a) 9 b) 2 91 c) 91
d) 2 91 e) 2 71
20. Dado el triángulo ABC, hallar el ángulo "B".
A
a) ArcSen
3 3
b) ArcTan
3
c) ArcTan3
d) ArcSec3
3
e) ArcTan3
3
30°
30°
B
21. En la figura, G es el centro del cuadrado ABCD. Hallar
la suma de los cuadrados de las distancias de los vértices
del cuadrado de la recta XY, si el lado del cuadrado es
L.
a) 2
L
b)
c)
d)
e)
2
2L
2
3L
2
4L
2
5L
x
B
2
N
M
A B
D
20°
G
3
C
C
y
C

22. El producto Sen2B . Sen2C del triángulo ABC es igual
a :
a)
15
b)
18
86
c)
125
105
256
105
d)
256
e)
86
125
A
B
10 15
23. Sea el triángulo ABC y sean a, b y c las longitudes de
los lados opuestos a los vértices A, B y C,
respectivamente.
Si se cumple la relación :
a
CosA
20
b
CosB
Entonces el triángulo ABC es :
a) Acutángulo.
b) Obtusángulo.
c) Isósceles.
d) Equilátero.
e) Rectángulo.
c
CosC
24. Las diagonales de un paralelogramo miden "a" y "b",
forman un ángulo agudo C. El área del paralelogramo
es :
a) abSenC
b) abCosC
c)
1
abCscC
2
d)
1
abSenC
2
e) 1
abCosC
2
25. Hallar el área del triángulo OB'C', si AB=4=BC,
O
M 1
AB
4
, AC=6.
M y M puntos medios en AC
1 2
y BC respectivamente AC // OC'
y BC // B'
C'
AO=OC'.
C
a)
29
7
3
29
b) 7
6
c)
29
7
7
d)
29
7
2
e)
29
7
24
A
M 1
C
O
M 2
26. Si en un triángulo, donde a, b, c son los lados opuestos
a los ángulos A, B, C se cumple que :
C’
B C
2
y b c a 2
Entonces : B A
2
es igual a :
a) 8
b) 4
c) 2
d) 0
e) 3
27. En un triángulo ABC, el ángulo C mide 60º y los lados
a 2 3 2 y b 2 3 2 .
Entonces, la medida del ángulo A es :
a)
b)
2
3
3
ArcTan
ArcTan
2
2
2
2
B
B’

c)
d)
e)
3
2
3
4
2ArcTan
ArcTan
ArcTan
2
2
2
2
2
2
28. En un triángulo ABC, se cumple :
SenC
2Sen(
A
B)
TanB 3 3 2 6
Hallar el valor del ángulo BAC.
a) 3
b) 6
2
c)
3
5
d)
12
3
e)
10
29. En un triángulo ABC, se cumple que :
m B m C 90º
; b c a 2
Hallar la medida del ángulo B.
a) 110º
b) 105º
c) 127º
d) 120º
e) 125º
30. Sea el triángulo ABC de lados AB = AC y BC 2 . Si
la bisectriz del ángulo B corta al lado opuesto en D y
BD = 1.
Entonces, los ángulos A y B son:
a) 60º ; 60º
b) 90º ; 45º
c) 100º ; 40º
d) 120º ; 30º
e) 150º ; 15º
31. En un triángulo ABC, C = 60º y a = 3b.
Determinar el valor deE= Tan(A B)
a) 4 3
b) 2 3
c) 3
2
d) 3
e) 1
32. En un triángulo rectángulo, la hipotenusa mide "c"
unidades y la longitud de la bisectriz de uno de los
c 3
ángulos agudos es unidades.
3
Hallar el área de la región delimitada por el triángulo
rectángulo dado.
a)
b)
c)
d)
e)
c 3
4
2
c 3
8
2
c 3
6
2
3c 6
2
3c 2
2
33. En un triángulo ABC con lados a, b y c, respectiva-
mente; se tiene :
Tan
A
2
1 y Tan
B
2
3
.
4
Determinar :
a
a
b
b
a) 50
b) 16
c) 49
d) 9
e) 25
34. Una diagonal de un paralelepípedo rectángulo forma
con las tres aristas concurrentes a un mismo vértice los
ángulos , y . El valor de :
3
a)
2
b) 2
5
c)
2
d) 3
e) 4
2 2 2
Sen Sen Sen es :

35. En la figura, se muestra un triángulo en el que se cumple:
CosA CosB
Luego el valor de a + b es :
2
4Sen
C
2
A
3c
a) 3c b)
2
5
d) c
3
5
e) c
2
c
b
c) 2c
36. En la figura mostrada, el triángulo ABC está inscrito en
una circunferencia de radio R. Si se cumple que :
2
c
2
a
2
2R
y la medida del ángulo B es 30º, los
valores de los ángulos A y C son respectivamente:
a) 45º y 105º
b) 35º y 115º
c) 60º y 90º
d) 30º y 120º
e) 25º y 125º
A
c
R
37. Dos circunferencias de radios 2u y 3u, tienen sus
centros separados una distancia igual a 4u. El Coseno
del ángulo agudo que forman las tangentes a ambas
circunferencias en un punto de corte, es igual a :
1
a)
2
1
d)
3
b)
1
e)
4
3
2
c)
B
B
1
2
38. En un triángulo ABC, se cumple :
3 2
a ( b
2
c )
3 2
b ( a
2
c )
5
( a
5
b )
Donde :
R : Circunradio del triángulo ABC
a
a
C
2
2abcR
C
Calcule :
P = SenA Sen2A + SenB Sen2B
3
a) 1 b) 2 c)
4
1
d)
2
3
e)
2
39. Del gráfico, ABC es un triángulo isósceles recto en "B" y
DBE es un triángulo equilátero.
Si : AC = 6
Calcular :
2
AP
2
BP
2
CP
B
P
A D E C
a) 18 b) 19 c) 9
d) 81 e) 27
40. En un triángulo ABC :
Calcular :
3
a)
4
6
d)
7
a
a
c
c
4
b)
3
2
e)
5
4Tan
B
2
Cot
A C
2
TanA TanB TanC
TanA TanC
7
c)
6
41. En el triángulo equilátero mostrado, calcular :
A
J
Cos(
15º
B
45º
3 ) Sec
2
C

a)
6 1
2
b) 3 1
c)
d)
e)
3 1
2
3 1
2
2 1
3
42. Si en un triángulo ABC :
Calcular :
2
a)
5
3
b)
7
4
c)
7
3
d)
5
1
e)
4
c
b
L
bCosA
cCosA
3
5
Tan
B C
2
Tan
A
2
43. En un triángulo ABC :
Cos2A + Cos2B + Cos2C = n
Las distancias del ortocentro a los lados del triángulo
son x ; y ; z.
Hallar : J xyz , si el circunradio mide 2
a) 2n 1
b) 2(n 1)
c) 2(1 n)
d) n 1
e)
4
2(
n 1)
44. Los lados de un cuadrilátero son a = 7; b = 8; c = 9;
d = 11.
Si su superficie es S = 33, calcular la tangente del
ángulo agudo formado por las diagonales.
a) 2 b) 2,3 c) 2,4
d) 1,8 e) 1,6
45. Dado un cuadrilátero ABCD, determine el valor de la
expresión.
E
1
a)
4
1
b)
12
d) 0
1
e)
6
2
bcCos
C
2
( b
2
c)
1
c)
3
2
adCos
( a
2
d)
46. Siendo A, B y C los ángulos internos de un triángulo,
para el cual se cumple :
2SenB SenA = Sen(A+B+C)+SenC
Calcule el valor de :
a) 1 b)
A
d) 1 e) 2
Cot
A
2
Cot
C
2
Cot
A
2
Cot
C
2
1
2
1
c)
2
47. En un triángulo acutángulo ABC, la circunferencia
descrita tomando como diámetro la altura relativa al
lado a, intercepta a los lados b y c, en los puntos P y Q
respectivamente.
Exprese el segmento PQ en función de los ángulos del
triángulo y del radio R de la circunferencia circunscrita
al triángulo.
a) 2RSenA SenB SenC
b) R SenA SenB SenC
c) R CosA CosB CosC
d) 3R CosA CosB CosC
e) R TanA TanB TanC
48. En un triángulo ABC, reducir :
P
2
a Sen(
B C)
SenB SenC
a) SenA SenB SenC
b) CosA CosB CosC
c) Sen (A + B + C)
d) Cos (A + B + C)
e) 2Cos (A + B + C)
2
b Sen(
C A)
SenC SenA
1
1
A
2
2
c Sen(
A B)
SenA SenB

49. En el triángulo ABC, se tiene : AB = 2, AC 6
'
V
b
Calcular : '
V
b
Donde : (V'b y Vb son bisectrices exterior e interior
respectivamente, relativo al lado b)
A
B
D
a) 2 3 b) 1 3
c) 2 3 d) 3 1
e) 2
45º
a
50. Dado un triángulo ABC, si : m C 30 30º º y
b
a
y a
Calcular : B Â ˆ 1
2
a) 30º
b)
ArcTan
c) ArcTan
3
3 2
7
d)
ArcTan
3
3
7
2
e) ArcTan
3
2 3
7
3
51. En el cuadrilátero ABCD de la siguiente figura, calcular:
Sen
Si : 2AD = AB = 3AC
1
a)
7
3
b)
4
A
2Cos
B C
3
c)
2
D
C
5
2
2
d)
3
1
e)
3
52. Los ángulos de un cuadrilátero ABCD están en
progresión geométrica de razón 3.
Calcular :
P = CosA CosB + CosB CosC +
CosC CosD + CosD CosA
1
a) 1 b)
2
5
d)
4
5
e)
2
1
c)
4
53. En un triángulo ABC, se cumple que :
CosA
a c
; CosB
a b
2b
2c
Calcular :
TanA + TanB + TanC
a) 7 b) 2 3 c) 13
d) 11 e) 2 5
54. En la figura R,
R ,
1
R y
2
R son los radios de las
3
circunferencias circunscritas a los triángulos ABC, ABP,
BCQ y ACS respectivamente.
Hallar "R".
R
1
1
; 2
R 2
P
; 4
R 3
a) 2 b) 1 c) 3
d) 2 e) 4
A
B
55. Los lados de un triángulo oblicuángulo ABC, miden :
b = (SenA + CosA)u
c= (SenA CosA)u
Además : a
6
u
2
Hallar la medida del mayor valor de A.
a) 60º b) 72º c) 54º
d) 65º e) 45º
Q
C
S

56. En un triángulo ABC, reducir :
M
( c
a) R b)
3
d) R e) 2
6R
bCosA)(
a cCosB)(
b aCosC)
Sen2ASen
2BSen2C
3
8R c)
3
4R
57. En un triángulo ABC, se cumple que :
Sen2A
Tan
Sen2B
A B
2
3Tan
Hallar la medida del ángulo "B"
a) 30º
b)
ArcTan
c) ArcTan
d) a o b
e) a o c
3
5
3
2
3Cos(
A
A B
2
58. En un triángulo ABC, se cumple que :
CotA + CotC = 2CotB
Luego se cumple que :
a) a + c = 2b
b) 2b ac
2
c)
2
a
2
c
d) b a c
2
e)
2
4b
2
a
2
2b
2
c
B)
59.Siendo ABC un triángulo de lados a, b y c, entonces
respecto a"K" podemos afirmar que :
K
2
a
2
a
2
b
2
b
2
c
2
c
a
a
a) K = 1 b) K = 2 c) K = 4
d) K 2 e) K 4
cCosB
bCosC
60. En un cuadrilátero inscriptible ABCD, de lados AB = a,
BC = b, CD = c y AD = d.
Calcular : R
a)
b)
c)
d)
ab
ad
ab
ac
ab
ad
ac
ab
a
e)
cd
bd
cd
bd
cd
bc
bd
cd
b c
abcd
d
SenA
SenB

Claves
Claves
a
e
d
c
d
b
b
e
b
c
e
d
a
b
b
a
b
e
b
e
a
a
d
d
e
a
b
a
b
d
a
b
c
b
c
d
e
d
e
b
d
e
e
c
a
c
a
c
a
c
d
b
a
d
b
d
d
c
d
c
01.
02.
03.
04.
05.
06.
07.
08.
09.
10.
11.
12.
13.
14.
15.
16.
17.
18.
19.
20.
21.
22.
23.
24.
25.
26.
27.
28.
29.
30.
31.
32.
33.
34.
35.
36.
37.
38.
39.
40.
41.
42.
43.
44.
45.
46.
47.
48.
49.
50.
51.
52.
53.
54.
55.
56.
57.
58.
59.
60.

TRIGONOMETRÍA
Í N D I C E