Propiedades de las transformaciones
Propiedades de las transformaciones
Propiedades de las transformaciones
You also want an ePaper? Increase the reach of your titles
YUMPU automatically turns print PDFs into web optimized ePapers that Google loves.
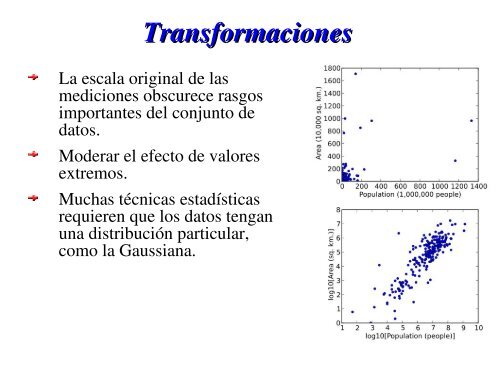
Transformaciones<br />
La escala original <strong>de</strong> <strong>las</strong><br />
mediciones obscurece rasgos<br />
importantes <strong>de</strong>l conjunto <strong>de</strong><br />
datos.<br />
Mo<strong>de</strong>rar el efecto <strong>de</strong> valores<br />
extremos.<br />
Muchas técnicas estadísticas<br />
requieren que los datos tengan<br />
una distribución particular,<br />
como la Gaussiana.
<strong>Propieda<strong>de</strong>s</strong> <strong>de</strong> <strong>las</strong> <strong>transformaciones</strong><br />
Cada dato puntual xi es reemplazado por su valor<br />
transformado y i<br />
= f(x i<br />
), don<strong>de</strong> f es una función.<br />
<br />
Se aplica una transformación a los datos para: a)<br />
hacer su distribución más simétrica; b) para que<br />
cumpla con <strong>las</strong> suposiciones <strong>de</strong> algún proceso <strong>de</strong><br />
inferencia estadística, o c) para po<strong>de</strong>r interpretar<br />
mejor los datos.<br />
<br />
Generalmente, la función f es invertible y continua.
Transformaciones <strong>de</strong> potencias<br />
Se aplican para hacer la distribución <strong>de</strong> valores mas simétrica.<br />
Son útiles cuando se aplican a distribuciones unimodales <strong>de</strong><br />
datos con valores positivos.
<strong>Propieda<strong>de</strong>s</strong> <strong>de</strong> <strong>las</strong> <strong>transformaciones</strong> <strong>de</strong> potencias<br />
<br />
<br />
<br />
<br />
Se usan para distribuciones unimodales <strong>de</strong> variables<br />
positivas. Estas funciones son estrictamente<br />
crecientes → preservan el or<strong>de</strong>n<br />
Para λ = 1 los datos permanecen esencialmente sin<br />
cambios.<br />
Para λ > 1, los valores más gran<strong>de</strong>s se incrementan<br />
más que los pequeños → ayudan a producir simetría<br />
cuando se aplica a datos con sesgo negativo.<br />
Para λ < 1, los valores más gran<strong>de</strong>s <strong>de</strong>crecen más<br />
que los pequeños → ayudan a producir simetría<br />
cuando se aplica a datos con sesgo positivo.
Para escoger un valor apropiado para λ se<br />
utiliza el estadístico d λ<br />
:<br />
d λ<br />
= |media(λ) – mediana(λ)|<br />
<br />
<br />
dispersión(λ)<br />
La medida <strong>de</strong> dispersión pue<strong>de</strong> ser el IQR o el<br />
MAD.<br />
Se elige la λ que produce el dλ más pequeño,<br />
esencialmente mediante prueba y error.<br />
Generalmente los valores <strong>de</strong> prueba se eligen a<br />
intervalos <strong>de</strong> 0.5 o 0.25.
Anomalías estandarizadas<br />
• Las <strong>transformaciones</strong> también pue<strong>de</strong>n ser útiles cuando nos interesa<br />
trabajar simultáneamente con conjuntos <strong>de</strong> datos que están<br />
relacionados pero que no son estrictamente comparables. Un<br />
ejemplo serían datos que están sujetos a variaciones estacionales.<br />
• Transformación <strong>de</strong> los datos en términos <strong>de</strong> anomalías<br />
estandarizadas:<br />
• El hecho <strong>de</strong> transformar datos no-gaussianos <strong>de</strong> acuerdo a z no los<br />
hace más gaussianos.<br />
• Se trata <strong>de</strong> remover la influencia <strong>de</strong> la posición y <strong>de</strong> la dispersión<br />
<strong>de</strong>l conjunto <strong>de</strong> datos.<br />
• z es adimensional.<br />
• Un conjunto <strong>de</strong> datos que ha sido transformado en anomalías<br />
estandarizadas tendrá media = 0 y s = 1.
SOI = Z Tahiti<br />
- Z Darwin<br />
Darwin<br />
Tahiti
Promedios corridos<br />
(moving average, running mean)<br />
Se utilizan generalmente con series <strong>de</strong> tiempo para suavizar <strong>las</strong><br />
fluctuaciones <strong>de</strong> corto plazo o alta frecuencia y para enfatizar <strong>las</strong><br />
ten<strong>de</strong>ncias <strong>de</strong> largo plazo o ciclos.<br />
Es similar al filtro paso-bajo utilizado en el procesamiento <strong>de</strong><br />
señales.<br />
Dado un conjunto <strong>de</strong> datos y un tamaño fijo para los subconjuntos, el<br />
promedio corrido se obtiene calculando primero el promedio <strong>de</strong>l<br />
primer subconjunto; <strong>de</strong>spués se toma el siguiente subconjunto hacia<br />
a<strong>de</strong>lante, consi<strong>de</strong>rando el tamaño elegido, y se calcula su promedio.<br />
Este proceso se repite en toda la serie <strong>de</strong> datos original. La línea<br />
que une todos los promedios es el promedio corrido.
Técnicas <strong>de</strong> análisis para datos en pares<br />
<br />
Para cada observación en un conjunto <strong>de</strong> datos existe una<br />
observación correspondiente en la misma fecha en otro<br />
conjunto <strong>de</strong> datos.<br />
<br />
Diagrama <strong>de</strong> dispersión o gráfico x-y<br />
Diagrama <strong>de</strong> dispersión o gráfico x-y : Es una colección<br />
<strong>de</strong> puntos en el plano cuyas coor<strong>de</strong>nadas cartesianas son<br />
los valores <strong>de</strong> cada elemento <strong>de</strong> la pareja <strong>de</strong> datos.<br />
Permiten examinar con facilidad características tales como<br />
ten<strong>de</strong>ncias, tipo <strong>de</strong> relación entre <strong>las</strong> variables,<br />
aglomeración <strong>de</strong> una o <strong>de</strong> ambas variables, cambios en la<br />
dispersión <strong>de</strong> una variable como función <strong>de</strong> la otra y<br />
valores extremos o atípicos.
T Max
Coeficiente <strong>de</strong> correlación lineal <strong>de</strong> Pearson<br />
<br />
La covarianza es una medida <strong>de</strong> cuánto varían dos variables en<br />
forma conjunta. La varianza es un caso especial <strong>de</strong> la<br />
covarianza con X = Y.<br />
<strong>Propieda<strong>de</strong>s</strong> <strong>de</strong> la covarianza:<br />
a) cov(X,X) = var(X) = s 2<br />
b) cov(X,Y) = cov(Y,X)<br />
c) cov(cX,Y) = c cov(X,Y), don<strong>de</strong> c = constante<br />
d) Si X y Y son in<strong>de</strong>pendientes, cov(X,Y) = 0 (el inverso no es<br />
necesariamente cierto)<br />
El coeficiente <strong>de</strong> correlación normaliza la covarianza, creando<br />
una cantidad adimensional que facilita la comparación entre <strong>las</strong><br />
variables.
<strong>Propieda<strong>de</strong>s</strong> <strong>de</strong> r xy :<br />
a) -1
Coeficiente <strong>de</strong> correlación <strong>de</strong> rangos <strong>de</strong><br />
Spearman<br />
<br />
<br />
<br />
Es un estadístico robusto y resistente.<br />
Es el coeficiente <strong>de</strong> correlación <strong>de</strong> Pearson pero calculado<br />
usando los rangos <strong>de</strong> los datos, es <strong>de</strong>cir, la posición que<br />
ocupa cada dato al ser or<strong>de</strong>nados en forma ascen<strong>de</strong>nte.<br />
El promedio <strong>de</strong> los enteros <strong>de</strong> 1 a n es (n+1)/2 y su<br />
varianza es n(n 2 – 1)/[12(n-1)].<br />
don<strong>de</strong> D i<br />
es la diferencia <strong>de</strong> los rangos para la i-ésima<br />
pareja <strong>de</strong> datos.
En caso <strong>de</strong> empates, e.d., cuando un valor particular<br />
aparece más <strong>de</strong> una vez, a todos esos valores se les<br />
asigna el rango promedio.<br />
Este coeficiente establece que tan bien <strong>de</strong>scribe una<br />
función monótona arbitraria la relación entre dos<br />
variables.<br />
A diferencia <strong>de</strong>l coeficiente <strong>de</strong> Pearson, no requiere<br />
suponer que la relación entre <strong>las</strong> variables es lineal.<br />
(ejercicio)
Matriz <strong>de</strong> Correlación<br />
Es una herramienta útil para mostrar simultáneamente <strong>las</strong><br />
correlaciones entre más <strong>de</strong> dos variables o conjuntos <strong>de</strong><br />
datos.<br />
Las correlaciones entre <strong>las</strong> variables se pue<strong>de</strong>n<br />
acomodar en un arreglo matricial: R = r i,j<br />
Para K variables hay K(K-1)/2 apareamientos distintos.<br />
Por lo tanto, solamente K(K-1)/2 <strong>de</strong> los K 2 elementos <strong>de</strong><br />
la matriz proporcionan información no redundante.<br />
Los elementos <strong>de</strong> la diagonal son iguales a 1.<br />
La matriz R es simétrica, es <strong>de</strong>cir, ri,j = r j,i<br />
, por lo tanto los<br />
valores por encima y por <strong>de</strong>bajo <strong>de</strong> la diagonal son como<br />
imágenes reflejadas.
Pearson<br />
Spearman
Matriz <strong>de</strong> Dispersión<br />
Es una extensión gráfica <strong>de</strong> la matriz <strong>de</strong> correlación.<br />
Es un arreglo <strong>de</strong> diagramas <strong>de</strong> dispersión <strong>de</strong> acuerdo<br />
con la lógica <strong>de</strong> la matriz <strong>de</strong> correlación.
Mapas <strong>de</strong> Correlación (onepoint correlation maps)<br />
La necesidad <strong>de</strong> trabajar con datos <strong>de</strong> un gran número <strong>de</strong> localida<strong>de</strong>s hace<br />
ineficiente el uso <strong>de</strong> matrices <strong>de</strong> correlación y/o <strong>de</strong> dispersión.<br />
Si se tiene una o más variables medidas en distintas localida<strong>de</strong>s, el arreglo<br />
geográfico <strong>de</strong> los sitios pue<strong>de</strong> usarse para organizar la información sobre la<br />
correlación en forma <strong>de</strong> mapa.
Autocorrelación temporal o correlación serial<br />
• Persistencia – ten<strong>de</strong>ncia <strong>de</strong> <strong>las</strong> condiciones meteorológicas a<br />
ser similares en períodos <strong>de</strong> tiempo sucesivos.<br />
• Autocorrelación temporal – es la correlación <strong>de</strong> una variable<br />
consigo misma en diferentes tiempos, pasados o futuros.<br />
También se <strong>de</strong>nomina correlación con retraso (lagged<br />
correlation).<br />
• Generalmente se utiliza el coeficiente <strong>de</strong> correlación <strong>de</strong><br />
Pearson.<br />
• El proceso <strong>de</strong> calcular autocorrelaciones pue<strong>de</strong> ser<br />
visualizado imaginando dos copias <strong>de</strong> una serie <strong>de</strong> n<br />
observaciones con una <strong>de</strong> <strong>las</strong> series <strong>de</strong>splazada cierto<br />
intervalo <strong>de</strong> tiempo con respecto a la otra.<br />
• La autocorrelación con retraso 1 es la medida <strong>de</strong> persistencia<br />
más comúnmente utilizada. En este caso se tienen n-1<br />
parejas <strong>de</strong> datos para calcular la correlación.
Autocorrelación con retraso k - Las dos series se <strong>de</strong>splazan entre<br />
sí más <strong>de</strong> una unidad <strong>de</strong> tiempo. Progresivamente habrá menos<br />
datos para calcular la correlación, por lo que generalmente sólo los<br />
primeros valores <strong>de</strong> k serán <strong>de</strong> interés; rara vez se calculan<br />
correlaciones para valores <strong>de</strong> k > n/2 o k > n/3.
Función <strong>de</strong> autocorrelación<br />
<br />
La colección <strong>de</strong> autocorrelaciones calculadas para varios retrasos o<br />
lags (k) es llamada la función <strong>de</strong> autocorrelación: r(k) = r k<br />
Una función <strong>de</strong> autocorrelación siempre comienza con r 0<br />
= 1.<br />
<br />
<br />
<br />
Típicamente una función <strong>de</strong> autocorrelación exhibe un <strong>de</strong>caimiento<br />
más o menos gradual hacia cero conforme k se incrementa, reflejando<br />
la relación estadística más débil que generalmente existe entre datos<br />
más alejados en el tiempo.<br />
Función <strong>de</strong> autocovarianza – Se multiplican <strong>las</strong> autocorrelaciones por<br />
la varianza <strong>de</strong> los datos.<br />
La aplicación <strong>de</strong> métodos estadísticos clásicos que requieren la<br />
in<strong>de</strong>pen<strong>de</strong>ncia <strong>de</strong> los datos en una muestra, pue<strong>de</strong> conducir a<br />
resultados engañosos cuando <strong>las</strong> series <strong>de</strong> datos son fuertemente<br />
persistentes.
Información que proporciona la función<br />
<strong>de</strong> autocorrelación<br />
Detecta si un proceso es o no aleatorio.<br />
Detecta que tan rápido cambia un proceso en el<br />
tiempo.<br />
Detecta si el proceso tiene una componente<br />
periódica y cuál pue<strong>de</strong> ser la frecuencia esperada.