Première STI 2D - Dérivées des fonctions usuelles - Parfenoff . org

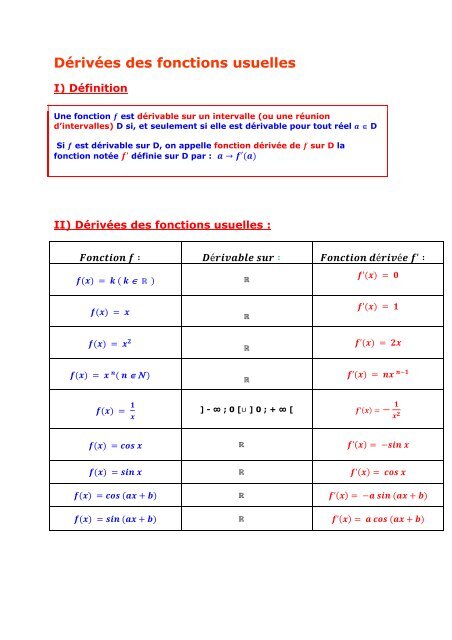
Dérivées des fonctions usuellesI) DéfinitionUne fonction est dérivable sur un intervalle (ou une réuniond’intervalles) D si, et seulement si elle est dérivable pour tout réel DSi est dérivable sur D, on appelle fonction dérivée de sur D lafonction notée ’ définie sur D par : →′II) Dérivées des fonctions usuelles : ∶ é ∶ éé ’ ∶ ’ ’ ’ ’ ] - ∞ ; 0 [∪ ] 0 ; + ∞ [ ’ ’ ’ ’ ’

III) Dérivées et opérations1) Somme de deux fonctionsLa fonction définie par = est dérivable sur D etsa dérivée est définie par ’ = ’ ’ .Exemples :Calculer les dérivées des fonctions suivantes :1°) = + sur On obtient ’ = 1 + 2°) = – 3 pour réel, ≠0On obtient ’ = – 3°) = cos + sin sur On obtient ’ = sin + cos 2) Produit d’une fonction par un réelLa fonction définie par = est dérivable sur D etsa dérivée est définie par ’ = ’.ExemplesCalculer les dérivées des fonctions suivantes :1°) =7 sur On obtient ’ = 7 = 21 2°) = pour réel, ≠0On obtient ’ =

3°) = 3 cos 5 sin sur On obtient ’ = 3 sin 5 cos 3) Produit de deux fonctionsLa fonction définie par = est dérivable sur D etsa dérivée est définie par ’ = ’ ’ExemplesCalculer les dérivées des fonctions suivantes :1°) = cos sur En posant = et = cos on a ’ = 2 et ’ = sin On obtient ’ = 2 cos + ( sin )’ = cos sin 2°) = cos sur En posant = et = cos on a ’ = 2 et ’ = sin On obtient ’ = 2 cos + ( sin )’ = cos sin 4 Inverse d’une fonctionLa fonction définie par = est dérivable sur l’ensemble D privédes réels où = 0 ( D { l ≠ 0 }) et sa dérivée est définie par: () = ’ ExemplesCalculer les dérivées des fonctions suivantes :1°) = sur En posant = 7 on a ’ = 2On obtient ’ =

2°) = sur ∖ , ∈ En posant =sin on a ’ = cos On obtient ’ = ² 5) Quotient de deux fonctionsLa fonction définie par =est dérivable sur l’ensemble D privédes réels où = 0 ( D { ≠ 0 }) et sa dérivée est définie par : = ’ ExemplesCalculer les dérivées des fonctions suivantes :1°) = sur ] -∞ ; [ ] ; + ∞ [En posant = 3 1 et = 5 3 on a ’ = 3 et ’ = 5On obtient ’ = = 2°) = sur ∖ 2 , ∈ En posant =sin et = cos on a ’ = cos et ’ = sinOn obtient ’ = ² ² ′=² = ² ² =²