Partie A Partie B

More documents

Recommendations

Info

EXERCICE 1 (5 points), commun à tous les candidats : <strong>Partie</strong> A 1) a) Résoudre dans l'ensemble des complexes l'équation z 2 – 2 z+ 4 = 0. Les solutions seront notées z ' et z'' sachant que la partie imaginaire de z ' est positive.∆ = (– 2) 2 – 4 × 4 × 1 = – 12 = (2 i 3) 2 donc les solutions sont : z' = 2 + 2 i 3 = 1 + i 3 et z " = z2− ' = 1 – i 3b) Ecrire z ' et z '' sous forme exponentielle.⎪⎧ cos θ = 1 2| z ' | = 1 + 3 2 = 2 et donc si θ est un argument de z ' alorssin θ =donc z ' = 2 e i 3 πet z " = z − ' = 2 e – i 3 π2) Quelle est la valeur exacte de (z') 2007 sous forme exponentielle puis algébrique.(z ' ) 2007 = ( 2 e )i 3 π 2 007 = 2 2 007 × e 2 007 i 3 π⎨⎩⎪32donc θ = π 3 + 2 k π2 007 π 3 = 669 π = π + 334 × 2 π donc π est un argument de (z ')2 007 et donc (z ') 2 007 = 2 2 007 e i π = – 2 2 007<strong>Partie</strong> B Le plan complexe est muni d'un repère orthonormal direct (O; ⎯→i ; ⎯→j ), on prendra pour unité graphique 2 centimètres. 1)Montrer que les points A (1 + i 3 ) et B(1 – i 3 ) sont sur un même cercle de centre O dont on précisera le rayon. Construire cecercle et placer les points A et B.OA = | 1 + i 3 | = 2 et OB = | 1 – i 3 | = 2 donc A et b sont sur le cercle de centre O de rayon 2.2) On considère la rotation r1 de centre A et d'angle – π . On note O' l'image de O par cette rotation.2Construire O'. Démontrer que O' a pour affixe : 1 – 3 + i ( 3 + 1).z O ' – z A = e – i π/2 (z O – z A ) ⇔ z O ' = z A – i (0 – z A )z O ' = 1 + i 3 + i (1 + i 3) = 1 + i 3 + i – 3 = 1 – 3 + i ( 3 + 1)3) On considère la rotation r2 de centre A et d'angle π . On note B' l'image de B par cette rotation.2Construire B'. Démontrer que B' a pour affixe 2 3 + 1 + i 3 .z B ' – z A = e i π/2 (z B – z A ) ⇔ z B ' = z A + i (z B – z A )z B ' = 1 + i 3 + i (1 – i 3 – 1 – i 3) = 1 + i 3 – 2 i 2 3 = 1 + 2 3 + i 34) Soit I le milieu de [OB] d'affixe zI : a) Vérifier que zI = 1 2 − i 3 .2z I = z O + z B= 0 + 1 – i 3 = 1 2 2 2 – i 32b) Calculer la mesure de l'angle ( ⎯⎯→AI , O'B')⎯⎯→( ⎯⎯→AI , O'B') ⎯⎯→= arg ⎜ ⎛ z B ' – z O '⎝ z ⎠ ⎟⎞I – z Az B ' – z O '= 1 + 2 3 + i 3 – 1 + 3 – i ( 3 + 1)z I – z A 12 – i 3=2 – 1 – i 3= 2 ×3 3 – i= (3 3 – i) ×1 – i 3 – 2 – 2 i 322– 1 – 3 i 33 3 – i– 1 – 3 i 3 = 2 × i – 3 3 (i – 3 3) (1 – 3 i 3)= 2 × = 2 × i – 3 i2 3 – 3 3 + 9 i × 31 + 3 i 3 1 + 9 × 328= 2 × i + 3 3 – 3 3 + 27 i28= 2 i variante 2 × i – 3 3 i (1 + 3 i 3)= 2 ×1 + 3 i 3 1 + 3 i 3 = 2 ion a donc ( ⎯⎯→AI , O'B') ⎯⎯→= arg ⎜ ⎛ z B ' – z O '⎝ z ⎠ ⎟⎞ = arg (2 i) = πI – z A 2c) Que peut-on en déduire pour la droite (AI) dans le triangle AO'B' ?(AI) est la hauteur issue de A du triangle AO'B'5) A tout nombre complexe z, on associe le nombre complexe Z = – 2 z + 2. Soit M un point d'affixe z. Déterminer l'ensemble Edes points M tels que : | Z | = 2. Préciser la nature de E.| Z | = 2 ⇔ | – 2 z + 2 | = 2 ⇔ | 1 – z | = 1 ⇔ Ω M = 1 où Ω est le point d'affixe 1.E est donc le cercle de centre Ω de rayon 1variante z M = x + i y| Z | = 2 ⇔ |– 2 (x + i y) + 2 | = 2 ⇔ | – 2 x – 2 i y + 2 | = 2 ⇔ (– 2 x + 2) 2 + (– 2 y) 2 = 4 ⇔ 4 x 2 – 8 x + 4 + 4 y 2 = 4⇔ x 2 – 2 x + y 2 = 0 ⇔ (x – 1) 2 + y 2 = 1 .
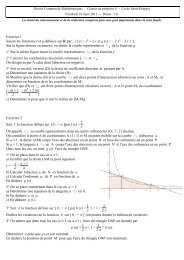
EXERCICE 2 (5 points), La courbe C f donnée en annexe est la représentation graphique de la fonction f définie sur] 0 ; + ∞ [ par f (x) = ln xx + 1.1) a) Etudier les variations de la fonction f sur ] 0 ; + ∞ [f est dérivable sur ] 0 ; + ∞ [ et pour tout réel x > 0,1x × x – 1 × ln xf '(x) =x 2 = 1 – ln xx 2f '(x) est donc du signe de 1 – ln x : 1 – ln x ≥ 0 ⇔ ln x ≤ 1 ⇔ x ≤ eb) En déduire les coordonnées du point de C f d’ordonnée maximale.f (e) = ln ee + 1 = 1 e + 1 donc le point d'ordonnée maximale est le point de coordonnées ⎝ ⎜⎛ e , 1 e + 1 ⎠ ⎟⎞2) Soit D la droite d'équation y = x. On cherche à calculer les coordonnées du point d'intersection de la courbe C et de la droite D. a) Démontrerque l'abscisse des points d'intersection de C f et D est solution de l'équation ln x – x 2 + x = 0.M(x, y) ∈ C f ∩ D ⇔ ⎨ ⎧ y = x⎩ y = f (x) ⇔ y = x⎩ ⎨⎧ x = f (x); donc l'abscisse de M est solution de l'équation f (x) = x.f (x) = x ⇔ ln xx + 1 = x ⇔ ln x + x = x2 (car x ≠ 0) ⇔ ln x – x 2 + x = 0b) Démontrer que l'équation ln x – x 2 + x = 0 admet une solution et une seule dans l'intervalle ] 0 ; + ∞ [ que l'on déterminera. Remarque : Onpourra étudier les variations de la fonction g définie sur ] 0 ; + ∞ [ par g (x) = ln x – x 2 + xg est dérivable sur ] 0 ; + ∞ [ et pour tout réel x > 0,g '(x) = 1 x – 2 x + 1 = – 2 x2 + x + 1xx < 0 donc g '(x) est du signe de – 2 x 2 + x + 1 = (x – 1)(– 2 x – 1)D'après les variations de g' on peut dire que, pour tout réel x ∈ ] 0 ; 1 ( ∪ ] 1 ; + ∞ [, g (x) < 0 et g (x) = 0 ⇔ x = 1.c) Déterminer alors les coordonnées du point d'intersection de C f et de D.L'abscisse des points d'intersection de C f et D est solution de l'équation ln x – x 2 + x = 0 c'est donc 1.Les coordonnées de ce point sont donc (1, 1).x 0 e + ∞signe de f '(x) + 0 –3) On définit une suite (U n ) n ∈ IN par son premier terme U 0 = 2 et, pour tout entier naturel n, U n + 1 = ln U n+ 1. a) Sur la représentation graphiqueci-dessous construire U 1 , U 2 et U 3 b) Démontrer par récurrence que, pour tout entier naturel n, U n appartient à [1 ; e].Initialisation : U 0 = 2 donc U 0 ∈ [ 1 , e]Hérédité : Si n est un entier naturel tel que U n ∈ [ 1 , e ] alors 0 < 1 ≤ U n ≤ e alors f (1) ≤ f (U n ) ≤ f (e), car f estcroissante sur ] 0 , e ], alors ln 12 + 1 ≤ U n + 1 ≤ 1 e + 1 < e et donc U n + 1 ∈ [ 1 , e ].Conclusion : la propriété est vraie pour n = 0, elle est héréditaire, elle est donc vraie pour tout entier naturel n.4) Déterminer le sens de variation de la suite (U n ) n ∈ IN .On démontre, par récurrence que, pour tout entier naturel n, U n ≥ U n + 1Initialisation : U 0 = 2 et U 1 = ln 22 + 1 < U 0Hérédité : si n est un entier naturel vérifiant U n ≥ U n + 1 .On sait que f est croissante sur ] 0 , e ], et que pour tout entier naturel n, U n et U n + 1 appartiennent à [1 , e] ⊂ ]0 , e]on peut donc dire que : f (U n + 1 ) ≤ f (U n ) c'est à dire U n + 2 ≤ U n + 1 .Conclusion : la propriété est vraie pour n = 0, elle est héréditaire, elle est donc vraie pour tout entier naturel n.Variante. U n + 1 – U n = f (U n ) – U n = ln (U n)+ 1 – UU n = ln U n + U n – (U n ) 2= g (U n)n U n U non a vu que, pour tout réel x > 0, g (x) ≤ 0 donc g (x) ≤ 0 donc Uxn + 1 – U n ≤ 0.La suite (U n ) est donc décroissante.5) a) Montrer que la suite (U n ) n ∈ IN est convergente. On note l sa limite.La suite (U n ) est décroissante et minorée, elle est donc convergente.b) Déterminer la valeur exacte de l.lim U n + 1 = lim U n = l et lim U n + 1 = lim f (U n) = f (l ) car lim U n = l et f continue en l .n → +∞ n → +∞ n → +∞ n → +∞ n → +∞l est donc solution de l'équation f (x) = x et cette équation a pour unique solution 1 donc l = 1.f (x)x 0 1 + ∞signe de g '(x) + 0 –0g (x)U n
Page 4 and 5: EXERCICE 5 (5points), commun à tou
Page 8 and 9: EXERCICE 2 (5 points), à traiter p
Page 10 and 11: EXERCICE 5 (5points), commun à tou
Page 12: EXERCICE 1 (5 points), commun à to

Partie A Partie B

Create successful ePaper yourself

Delete template?

Save as template?