S= och v=

Lösningar Kapitel 6 Heureka B (ASJ)
6.1 Se facit.
6.2 a) Centripetalaccelerationen a beror av farten v och banradien r.
=
Farten kan uttryckas med hjälp av omloppstiden
Med v =
får vi att =
b) Centripetalkraften får vi genom att multiplicera centripetalaccelerationen vi fick, med
massan.
17 N
6.3 När centripetalkraften slutar verka fortsätter pucken i tangentens riktning.
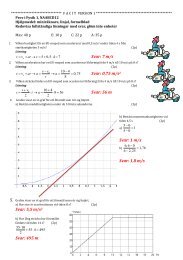
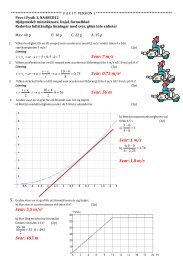
a) Puckens väg från P1 till P2 har längden s och farten v
S=
och v=
b) Från punkten är banan en rät linje som tangerar cirkeln, enligt
figuren. På 0,75 s rör sig pucken sträckan 0 ,75 v = 1,77 m i
riktningen "sydväst" som i figuren

6.4 a) Klossen rör sig i en cirkel med radien r = 0,2 m. Friktionen skapar en
centripetalkraft. Klossen roterar 0, 5 varv per sekund. Klossens fart är då
v =
= 0,2 m/s.
Nu kan vi beräkna centripetalaccelerationen
Eftersom klossens massa m är 0,6 kg blir centripetalkraften, eller i det här fallet
friktionskraften F = m 1,2 N
b) Vi ser att 1,2 N är en kraft som inte är större än maximal friktionskraft.
Om radien i klossens bana blir större, blir farten v=
Varvtiden T=2s ändras inte
större.
Centripetalkraften är nu 1,5 N. Vi använder sambandet F=m
v=
Alternativ lösning:
. Nu med lite matte får vi att r=
Här lönar det sig att införa storheten vinkelhastighet ( ), enligt formeln
Uttrycket för centripetalaccelerationen förenklas då till =r
6.5 a) Vi beräknar centripetalkraften:
F = m·
= 0,7
6,3 N
b) Centripetalkraften är resultanten till spännkraften S i tråden (riktad uppåt) respektive
tyngdkraften:
F = S - mg
Vi löser ut S:
S = F+ mg = 6,3 + 0,70. 9,82 13 N
.

6.6 a) Vi beräknar först hur stor centripetalkraften F ska vara
F=m·
b) Resultanten till normalkraften N ( som är riktad uppåt) och tyngdkraften, måste vara lika
med F:
F = mg - N, vilket medför att N = m·g-F=1500·9,82-1900
6.7 Eftersom tyngden är lika med centripetalkraften har vi följande samband:
=
. Efter förenkling med m får vi att g=
centripetalaccelerationen.
v= √ = √
alltså tyngdaccelerationen är lika med
6.8 a) Om vi betecknar j ordens radie med R = 6,38· m och omlopps tiden
T = 24·3600 s blir farten v=
Centripetalaccelerationen blir då =
Det betyder med andra ord, att centripetalkraften F på1kg är 34 mN
.
= 34mN/kg
b) Lodrätt uppåt verkar fjäderns kraft , lodrätt nedåt jordens dragningskraft
c) F är resultanten till och ,
F= =0,034+9,78=9,81N
6.9 a) För att Bodils sluthastighet ska ha rätt riktning måste hon springa längs tangenten
till cirkelbanan. Vi använder Pythagoras sats för att räkna ut sträckan
√ =3,3m (3,286 behåll i räknaren)
b) Hennes sluthastighet v ska vara lika stor som L:s konstanta fart:
(3,298, behåll i räknaren)

Om vi antar att Bodils ansats tar tiden t har vi att v = at (samband l) eftersom
rörelsen är likformigt accelererad utan begynnelsehastighet. Vi vet dessutom att
(samband 2) Om vi delar samband 2 med samband 1 får vi att:
=2s, som är ju tiden för ett halvt varv. Se figuren i facit.
6.10. Den sökta uppåtriktade kraften mot hinkens botten är lika stor som bottnens
nedåtriktade kraft N på stenen. Tillsammans med tyngden utgör N den nedåtriktade
centripetalkraften. Med matte och siffror får vi:
(samband 1)
På samma sätt för den mindre stenen:
3 + 0,25·9,82=
(samband 2)
Både v och r är samma för stenarna. Samband 2 ger:
Sätter in i (samband l) och får:
N = 0,4 ·21,8 - 0,4·9,82 = 4,8 N
Kraften från stenen på hinkens botten är lika stor (kraft och reaktionskraft), alltså 4,8 N
uppåt.
6.11 Se facit.
6.12
Låt m betyda raketens massa och M jordens.
Med jordens radie R = 6,38· m och raketens okända avstånd r från jordens
medelpunkt får vi följande ekvation med hjälp av gravitationslagen:
som efter lite matte blir: =2 eller √
Höjden över jordytan blir då: √ (√ )
6.13 Se facit.

6.14 I sambandet
(gravitationslagen), sätter vi in
Med data som finns i uppgiftstexten, kan ni enkelt beräkna tyngdkraften på de tre
planeterna.
a) 3,7N, b) 9,8N, c) 24N
6.15 Se facit.
6.16 Jordens dragningskraft är centripetalkraft.
Vi betecknar satellitens massa med m och jordens massa med . Kraftekvationen och
gravitationslagen ger oss följande samband:
För satellitens fart v gäller
Vi dividerar med m i båda leden i samband (l) och sätter in i samband(2):
√
, korsmultiplikation leder till
som ger
Eftersom r räknas från jordens medelpunkt, är höjden över jordytan egentligen
35,8· 5,6 jordradier.
6.17 a) Jordens dragningskraft är centripetalkraft. Kraftekvationen och
gravitationslagen ger följande ekvation:

Med r = 6,38 + 1 = 7,38 m = 5,98· kg får vi att
√
b) Se facit.
=7,35
6.18 Vi förutsätter i den här uppgiften att Jordens bana kring solen är en cirkel.
Solens dragningskraft är centripetalkraften. Kraftekvationen och gravitationslagen
som vanligt, ger oss följande ekvation:
Dessutom vet vi att
På samma sätt som vi gjorde i lösningen till 6.16 kombinerar vi (l) och (2), och får
följande,
Detta leder till att: =
eftersom vi förenklar med jordens massa.
. Med siffror får vi
6.19 a) Av figuren framgår att amplituden är 0,30 m.
b) Skuggan utför en hel period, från högsta läget till lägsta och tillbaka igen, samtidigt som
hjulet roterar ett helt varv. Detta tar 2 sekunder, därför är skuggans period också 2
sekunder.
c) Skuggans hastighet är lika stor som den lodräta komposanten av bollens hastighet.
Mitt emellan högsta och lägsta läget är bollens hastighet riktad vertikalt. I dessa
ögonblick har skuggan lika stor fart som bollen.

Matematiskt betyder detta (se figuren ovan)
6.20 a) Sinusfaktorn varierar ju mellan l och -l, vilket gör att y varierar mellan -0,15
och O,15. Amplituden är alltså 0,15 m.
b) Sinusfaktorn går genom en hel period när vinkeln ( ) växer med radianer.
Det betyder att tiden ska öka 0 = 0,63 s. Perioden är alltså 0,63 s.
Den här delen av uppgiften kan vi lösa på ett alternativt sätt också.
En jämförelse med det allmänna sambandet y = A sin visar att = 10 rad/s.
Eftersom
får vi att
c) För att få hastigheten v deriverar vi elongationsfunktionen (y = A sin med
avseende på t ( Glöm inte att "Inre derivatan" är 10.)
Hastigheten är 1,5 ·cos ( ) m/s.
d) Cosinusfaktorn varierar mellan -l och l, vilket betyder att hastigheten varierar
mellan-1,5 m/s och 1,5 m/s.
Största farten är (hastighetens "amplitud") alltså 1,5 m/s.
e) För att få accelerationen a deriverar vi hastigheten v med avseende på tiden:
Accelerationen är
=1,5 (m/
Resultatet visar att den maximala accelerationen är 15m/s2

6.21
a) Sträckan 2 · A = 2 ·0,46 m = 0,92 m genomlöps på 1s. Genomsnittsfarten är
0,92 m/s.
b) Eftersom elongationen är y = A· är hastigheten
=A
Mitt emellan ytterlägena: y = -A och y = A är y = O, eftersom sinusfaktorn är noll.
Samtidigt har cosinusfaktorn sitt största eller minsta värde, l eller -l, så att hastighetens
största belopp är =
Maximala farten är alltså 1,4 m/s.
c) Om A = 0,46 m och 2 (rad/s) får vi att
6.22
y = 0,46 sin
a) Att kurvan är en cirkel ser vi först när vi kvadrerar och adderar de två ekvationerna:
=1, trigonometriska ettan
vi får då: √ Varje punkt (x, y) på kurvan har alltså avståndet 3 längdenheter
till origo. Kurvan är en cirkel med radien 3 enheter.
b) När t växer med sekunder, genomlöper sinus- och cosinusfaktorerna båda
en hel period och partikeln fullbordar ett varv i banan. Omloppstiden är alltså 6,3 s.
c) Radien i denna cirkel är 3 enheter som förut, men nu växer vinklarna dubbelt så fort.
Omloppstiden blir hälften så stor, alltså
d) Sätt x = 3 · och y = 3 ·sin
På 5 sekunder ska vinkeln växa med 2 radianer. Om vinkelhastigheten är får vi
följande:
x = 3 ·
och y = 3 ·sin
insättning i ekvationerna ovan ger:
e) Jämförelse med ekvationerna i d) ger att r betyder radien i cirkelbanan och T är
omloppstiden.

6.23 Kraften F som drar ut fjädern är direkt proportionell mot förlängningen x:
F = k·x, där k kallas för fjäderkonstanten.
Det medför att x=
Fjädern blir 2cm längre.
6.24 Se facit.
6.25 Se boken för figur
a) I läge A har vagnen bromsats in och ska börja accelerera mot jämviktsläget. Kraften 18
N är alltså riktad åt höger.
b) I läge B (jämviktsläget) är farten maximal, och kraften övergår från att vara
accelererande till att vara retarderande (bromsande). Den "byter tecken" och är alltså
noll.
c) I läge C är fjädern lika mycket utdragen som den är sammanpressad i läge A. Kraften
har alltså storleken 18 N men är riktad åt vänster.
6.26
a) När fjädern trycks ihop 0,2 m blir dess kraft18 N. Fjäderkonstanten k är alltså
b) Vi vet att svängningstiden T = 2 √
Frekvensen f =
√
=
är alltså svängningstidens inverterade värde:
√
6.27 Av figur l här under, framgår att den nedåtriktade
resultanten till fjäderkraften och tyngdkraften i det övre läget är
4N.

Då måste resultanten i det nedre läget också ha storleken 4N, men vara uppåtriktad. Figur 2
visar att fjäderns kraft nu måste vara 10N och riktad uppåt för att resultanten ska bli 4N.
6.28
Svängningstiden är 2s. Då är vinkelhastigheten
Dessutom är massan m = 0,6 kg och amplituden A = O, 1 m.
a) Maximala farten är:
b) Maximala accelerationen inträffar i vändlägena, där den är
Kraften i dessa lägen är då lika med:0,6·0, l = 0,59 N
Kommentar: Man kan också utnyttja att fjäder konstanten är
Kraften i ett vändläge är fjäderkonstanten gånger fjäderns längdändring, som där är lika
med amplituden.
c) Accelerationen och fjäderkraften är proportionella mot elongationen. Vi har
sett att a = där y är elongationen. Om y är 0,05 m blir accelerationen lika med
Dess storlek (belopp) är alltså 0,49

6.29 a) När vagnen är i sitt jämviktsläge påverkas den av två lika stora
fjäderkrafter, som tar ut varandra. Vi antar att fjädrarna drar åt var sitt håll
med kraften F. Om vagnen flyttas sträckan x åt höger blir den vänstra
fjäderns kraft F+k·x,
(k = 30 N/m). Samtidigt minskar kraften från den högra fjädern lika mycket, med k· x,
alltså och den blir F - k· x. Den resulterande kraften drar åt vänster och har storleken
F
Exakt likadant resonemang blir det när vagnen flyttas åt vänster. Se
figuren!
b) Vagnen "känner" att fjäderkonstanten är
Svängningstiden √
= √
6.30 Fjäderkonstanten k får vi ur jämviktsvillkoret mg = kb
Detta uttryck sätter vi in i formeln för svängningstiden:
6.31 Vinkelhastigheten är
a) H astighetens maximum är
√
=
b) Den maximala accelerationen är och maximala kraften =m
√
√
√

6.32
a) I "parallellfallet" sträcks båda fjädrarna1cm och sammanlagda fjäderkraften blir
I "seriefallet" drar fjädrarna med lika stora krafter åt var sitt håll i föreningspunkten.
Förlängningarna blir lika stora. Den sammanlagda förlängningen är 1cm.Varje fjäder
förlängs alltså 0,5 cm. Kraften som behövs för detta är
b) När 1cm förlängning kräver 0,8 N är fjäderkonstanten 80 N/m. I "serie"-fallet kräver exakt
lika mycket förlängning 0,2N som motsvarar en fjäderkonstant på 20N/m
Eftersom √
I parallellfallet √
I seriefallet √
får vi följande:
=1,4s
6.33 Kraften F på stenen är proportionell mot avståndet r till jordens centrum:
(l)
mg = K R (2)
Här betyder m stenens massa, R jordradien och K en konstant. Genom att dividera (l) med
(2) får vi:
varifrån med korsmultiplikation får vi att F=
Kraften som verkar på stenen under resan genom hålet är en kraft som vill återföra stenen
till jämviktsläget med"fjäderkonstanten"
Rörelsen är en harmonisk svängning med svängningstiden:

84minuter
√
√
= √
= √
Stenen dyker alltså upp igen efter 84 min.
sekunder som är ungefär
Enkel resa tar 42 min, vilket faktiskt också gäller om hålet borras "snett", t ex från
Stockholm till London eller från Stockholm till Beijing. Se Lasse Samuelssons ”PIM” film
på lsswebb.
6.34
a) Anta att fjäderns förlängning är när vikten hänger i jämvikt. Då gäller att
= mg. Energin i fjädern är då
När fjädern dras ut sträckan y blir den nya förlängningen s = +y och fjäderns energi
blir då :
Ökningen är:
OBS. Om vi faktoriserar uttrycket (
termen
b) Lägesenergin i tyngdkraftfältet avtar med mg·y
c) Nettotillväxten av energin hos systemet fjäder och vikt, alltså det arbete som krävs blir
Den första delkraften får man ganska enkelt genom viktens tyngdkraft. Den resterande
delen av medelkraften multiplicerad med y ger det sökta arbetet. Se även figuren, där
arbetet fås som "area under grafen"!
.
),
=

6.35 Se facit.
6.36 Totala energin är summan av rörelseenergin O,7 J och potentiella energin O,9 J i
samma ögonblick, alltså 1,60 J. jämviktsläget har vi endast rörelseenergi, och om farten där
betecknar vi v kan vi skriva
och räkna ut √
6.37 Vi betecknar den potentiella energin med och den kinetiska (rörelse) energin
med
+
Eftersom svängningsrörelsen är harmonisk är
ju elongationen som vi är vana vid nu.
Vidare är
Om y=
där k är ju fjäderkonstanten och y är
(I vändlägena är ju rörelseenergin noll.) ( A är amplituden)
får vi att den potentiella energin
Den kinetiska energin blir då
Bråkdelen är alltså 3/4.
6.38 En trådpendel med längden l har svängningstiden √
Vi löser ut l och sätter in T = 2s och g=9,82m/ (
(
)
)
(
)

6.39 Antalet sekunder på ett dygn är 24 86 400.
a) Uppe på berget utför pendeln 86 400-26=86376 hela svängningar på 86 400
sekunder. Svängningstiden är då
6.40 Se facit.
= 1,0003 s
b)Pendelns längd l är lika i de båda fallen
√
och √
Vi dividerar de två sambanden ledvis, löser ut och
sätter in tiderna :
6.41 Vi kallar utslagsvinkeln i vändläget Se figuren!
√
Eftersom hastigheten är noll i just vändlägena, är centripetalaccelerationen också noll.
Det betyder att vi inte har någon centripetalkraft. Då måste spännkraften S i tråden
och tyngd kraftens komposant längs radien vara lika stora och motsatt
riktade, alltså ta ut varandra. Den resulterande kraften på pendelkulan i ett vändläge är
alltså tyngdkraftens komposant vinkelrätt mot pendeltråden. Dess storlek är
Accelerationens belopp (storlek) är då
6.42
a) I formeln för svängningstiden byt m mot 2m. Då ser ni att om man fördubblar massan hos
en fjäder pendel, ökar svängningstiden med faktorn √
(
)

svängningstiden enligt sambandet T = √
när fjäderkonstanten k är känd. Svaret blir här √
är proportionell mot kvadratroten ur massan
b) Trådpendelns svängningstid beror inte av massan.(massan finns inte med i formeln!)
Alltså ingen ändring när massan ändras.
6.43 I ett ögonblick när utslagsvinkeln är utgörs centripetalkraften av resultanten
till spännkraften S och tyngdkraftskomposanten i trådens riktning:
Med lite matte:
Vi måste uttrycka
aktuella utslagsvinkeln
Om är lägesenergin mgh (
termen med saker som vi vet. Vi räknar kulans rörelseenergi vid den
När kulan släpps från ett vändläge säger energilagen att
Vi låter kulans lägesenergi när den är rakt
under upphängningspunkten vara noll, Se
figuren! När kulan förs ut till ett vändläge
blir dess lägesenergi ,
Dividerar med l och multiplicerar med 2 (det som är markerat)
enligt figuren

6.44 Se facit.
6.45 a) Vagnens rörelseenergi omvandlas till potentiell energi i fjädern, alltså
Om en konstant kraft F ska uträtta det arbete som förmedlar omvandlingen, måste vi ha att
Det betyder att F=
b) Under inbromsningen utför vagnen en fjärdedels harmonisk svängning. Den har
hela tiden kontakt med fjädern och uppför sig som om den vore fäst vid den.
Tiden som går åt är
√
=
√
c) Rörelsemängdens ändring är m· v. Om en konstant kraft F ska åstadkomma denna ändring
ska dess impuls uppfylla villkoret
Enligt ekvationen under punkt a) är och vi får då
√
√
√
√