Prezentacja: szeregi liczbowe
Prezentacja: szeregi liczbowe
Prezentacja: szeregi liczbowe
You also want an ePaper? Increase the reach of your titles
YUMPU automatically turns print PDFs into web optimized ePapers that Google loves.
Szeregi <strong>liczbowe</strong><br />
Szeregi <strong>liczbowe</strong><br />
Szeregi potęgowe<br />
Szeregi Fouriera<br />
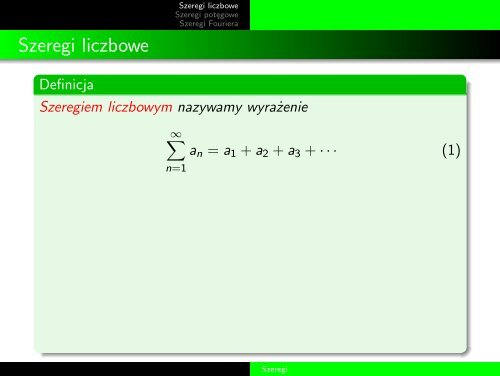
Definicja<br />
Szeregiem liczbowym nazywamy wyrażenie<br />
∞∑<br />
a n = a 1 + a 2 + a 3 + · · · (1)<br />
n=1<br />
Szeregi
Szeregi <strong>liczbowe</strong><br />
Szeregi <strong>liczbowe</strong><br />
Szeregi potęgowe<br />
Szeregi Fouriera<br />
Definicja<br />
Szeregiem liczbowym nazywamy wyrażenie<br />
∞∑<br />
a n = a 1 + a 2 + a 3 + · · · (1)<br />
n=1<br />
Liczby a n , n = 1, 2, . . . nazywamy wyrazami szeregu.<br />
Szeregi
Szeregi <strong>liczbowe</strong><br />
Szeregi <strong>liczbowe</strong><br />
Szeregi potęgowe<br />
Szeregi Fouriera<br />
Definicja<br />
Szeregiem liczbowym nazywamy wyrażenie<br />
∞∑<br />
a n = a 1 + a 2 + a 3 + · · · (1)<br />
n=1<br />
Liczby a n , n = 1, 2, . . . nazywamy wyrazami szeregu.Sumę<br />
s n =<br />
n∑<br />
a k (2)<br />
k=1<br />
nazywamy n-tą sumą częściową szeregu. Jeżeli istnieje granica<br />
lim n→∞ s n = S, to szereg (1) nazywamy zbieżnym.<br />
Szeregi
Szeregi <strong>liczbowe</strong><br />
Szeregi <strong>liczbowe</strong><br />
Szeregi potęgowe<br />
Szeregi Fouriera<br />
Definicja<br />
Szeregiem liczbowym nazywamy wyrażenie<br />
∞∑<br />
a n = a 1 + a 2 + a 3 + · · · (1)<br />
n=1<br />
Liczby a n , n = 1, 2, . . . nazywamy wyrazami szeregu.Sumę<br />
s n =<br />
n∑<br />
a k (2)<br />
k=1<br />
nazywamy n-tą sumą częściową szeregu. Jeżeli istnieje granica<br />
lim n→∞ s n = S, to szereg (1) nazywamy zbieżnym.<br />
W przeciwnym przypadku mówimy, że szereg jest rozbieżny.<br />
Szeregi
Szeregi <strong>liczbowe</strong><br />
Szeregi <strong>liczbowe</strong><br />
Szeregi potęgowe<br />
Szeregi Fouriera<br />
Definicja<br />
Szeregiem liczbowym nazywamy wyrażenie<br />
∞∑<br />
a n = a 1 + a 2 + a 3 + · · · (1)<br />
n=1<br />
Liczby a n , n = 1, 2, . . . nazywamy wyrazami szeregu.Sumę<br />
s n =<br />
n∑<br />
a k (2)<br />
k=1<br />
nazywamy n-tą sumą częściową szeregu. Jeżeli istnieje granica<br />
lim n→∞ s n = S, to szereg (1) nazywamy zbieżnym.<br />
W przeciwnym przypadku mówimy, że szereg jest rozbieżny.<br />
Liczbę S nazywamy sumą szeregu.<br />
Szeregi
Szeregi <strong>liczbowe</strong><br />
Szeregi potęgowe<br />
Szeregi Fouriera<br />
Przykłady. Znaleźć wzór na sumę s n i zbadać zbieżność szeregu<br />
∞∑<br />
a n .<br />
n=1<br />
1.<br />
2.<br />
3.<br />
4.<br />
∞∑<br />
n=1<br />
∞∑<br />
n=1<br />
∞∑<br />
n=1<br />
∞∑<br />
n=1<br />
300<br />
2 n ;<br />
2 n<br />
300 ;<br />
(−1) n ;<br />
1<br />
n(n + 1) .<br />
Szeregi
Achilles i żółw<br />
Szeregi <strong>liczbowe</strong><br />
Szeregi potęgowe<br />
Szeregi Fouriera<br />
Podany przez Zenona z Elei paradoks Achillesa i żółwia przedstawia<br />
się zazwyczaj tak: Achilles (słynący jako szybkobiegacz) ściga<br />
żółwia, który jest daleko w przodzie, gdy heros zaczyna bieg.<br />
Następnie Achilles dobiega do miejsca, w którym niedawno był<br />
żółw, ale w tym czasie zwierzak dochodzi już do następnego<br />
miejsca, które za chwilę osiąga Achilles, ale żółw dochodzi w tym<br />
czasie do nowego, Achilles znowu dobiega, ale żółw jest dalej, itd.<br />
A więc Achilles nigdy nie dogoni żółwia – konkludował Zenon.<br />
Szeregi
Achilles i żółw<br />
Szeregi <strong>liczbowe</strong><br />
Szeregi potęgowe<br />
Szeregi Fouriera<br />
Podany przez Zenona z Elei paradoks Achillesa i żółwia przedstawia<br />
się zazwyczaj tak: Achilles (słynący jako szybkobiegacz) ściga<br />
żółwia, który jest daleko w przodzie, gdy heros zaczyna bieg.<br />
Następnie Achilles dobiega do miejsca, w którym niedawno był<br />
żółw, ale w tym czasie zwierzak dochodzi już do następnego<br />
miejsca, które za chwilę osiąga Achilles, ale żółw dochodzi w tym<br />
czasie do nowego, Achilles znowu dobiega, ale żółw jest dalej, itd.<br />
A więc Achilles nigdy nie dogoni żółwia – konkludował Zenon.<br />
Paradoks Zenona można wyjaśnić przy pomocy szeregów.<br />
Szeregi
Achilles i żółw<br />
Szeregi <strong>liczbowe</strong><br />
Szeregi potęgowe<br />
Szeregi Fouriera<br />
Zadanie. Achilles znajduje się w odległości d od żółwia i ściga go<br />
z prędkością V . Żółw porusza się z prędkością v.<br />
Niech t 1 oznacza czas w jakim Achilles przebędzie odległość d, a<br />
s 1 — drogę przebytą przez żółwia w tym czasie.<br />
Szeregi
Achilles i żółw<br />
Szeregi <strong>liczbowe</strong><br />
Szeregi potęgowe<br />
Szeregi Fouriera<br />
Zadanie. Achilles znajduje się w odległości d od żółwia i ściga go<br />
z prędkością V . Żółw porusza się z prędkością v.<br />
Niech t 1 oznacza czas w jakim Achilles przebędzie odległość d, a<br />
s 1 — drogę przebytą przez żółwia w tym czasie.<br />
Ogólnie: t n oznacza czas w jakim Achilles przebędzie odległość<br />
s n−1 , a s n — drogę przebytą przez żółwia w czasie t n .<br />
Szeregi
Achilles i żółw<br />
Szeregi <strong>liczbowe</strong><br />
Szeregi potęgowe<br />
Szeregi Fouriera<br />
Zadanie. Achilles znajduje się w odległości d od żółwia i ściga go<br />
z prędkością V . Żółw porusza się z prędkością v.<br />
Niech t 1 oznacza czas w jakim Achilles przebędzie odległość d, a<br />
s 1 — drogę przebytą przez żółwia w tym czasie.<br />
Ogólnie: t n oznacza czas w jakim Achilles przebędzie odległość<br />
s n−1 , a s n — drogę przebytą przez żółwia w czasie t n .<br />
Obliczyć sumy szeregów ∑ ∞<br />
n=1 t n i ∑ ∞<br />
n=1 s n .<br />
Szeregi
Achilles i żółw<br />
Szeregi <strong>liczbowe</strong><br />
Szeregi potęgowe<br />
Szeregi Fouriera<br />
Zadanie. Achilles znajduje się w odległości d od żółwia i ściga go<br />
z prędkością V . Żółw porusza się z prędkością v.<br />
Niech t 1 oznacza czas w jakim Achilles przebędzie odległość d, a<br />
s 1 — drogę przebytą przez żółwia w tym czasie.<br />
Ogólnie: t n oznacza czas w jakim Achilles przebędzie odległość<br />
s n−1 , a s n — drogę przebytą przez żółwia w czasie t n .<br />
Obliczyć sumy szeregów ∑ ∞<br />
n=1 t n i ∑ ∞<br />
n=1 s n .<br />
Po jakim czasie Achilles dogoni żółwia<br />
Szeregi
Szeregi <strong>liczbowe</strong><br />
Szeregi potęgowe<br />
Szeregi Fouriera<br />
Zauważmy, że gdy szereg ∑ ∞<br />
n=1 a n jest zbieżny, to zarówno s n jak i<br />
s n−1 dążą do granicy S. Ponieważ a n = s n − s n−1 , więc<br />
lim n→∞ a n = 0. Mamy więc następujące twierdzenie<br />
Twierdzenie (warunek konieczny zbieżności szeregu)<br />
Jeżeli szereg ∑ ∞<br />
n=1 a n jest zbieżny, to jego wyraz ogólny a n dąży do<br />
0.<br />
Szeregi
Szeregi <strong>liczbowe</strong><br />
Szeregi potęgowe<br />
Szeregi Fouriera<br />
Zauważmy, że gdy szereg ∑ ∞<br />
n=1 a n jest zbieżny, to zarówno s n jak i<br />
s n−1 dążą do granicy S. Ponieważ a n = s n − s n−1 , więc<br />
lim n→∞ a n = 0. Mamy więc następujące twierdzenie<br />
Twierdzenie (warunek konieczny zbieżności szeregu)<br />
Jeżeli szereg ∑ ∞<br />
n=1 a n jest zbieżny, to jego wyraz ogólny a n dąży do<br />
0.<br />
Ten warunek nie jest wystarczający. Jest wiele szeregów, których<br />
wyraz ogólny a n dąży do 0, ale które są rozbieżne.<br />
Szeregi
Szeregi <strong>liczbowe</strong><br />
Szeregi potęgowe<br />
Szeregi Fouriera<br />
Zauważmy, że gdy szereg ∑ ∞<br />
n=1 a n jest zbieżny, to zarówno s n jak i<br />
s n−1 dążą do granicy S. Ponieważ a n = s n − s n−1 , więc<br />
lim n→∞ a n = 0. Mamy więc następujące twierdzenie<br />
Twierdzenie (warunek konieczny zbieżności szeregu)<br />
Jeżeli szereg ∑ ∞<br />
n=1 a n jest zbieżny, to jego wyraz ogólny a n dąży do<br />
0.<br />
Ten warunek nie jest wystarczający. Jest wiele szeregów, których<br />
wyraz ogólny a n dąży do 0, ale które są rozbieżne.<br />
Bardzo ważnym przykładem jest szereg harmoniczny:<br />
∞∑<br />
n=1<br />
1<br />
n = 1 + 1 2 + 1 3 + 1 4 + 1 5 + · · ·<br />
Szeregi
Szeregi <strong>liczbowe</strong><br />
Szeregi potęgowe<br />
Szeregi Fouriera<br />
Twierdzenie<br />
∑<br />
1. Jeżeli szereg ∞ a n jest zbieżny, to dla dowolnego c ∈ R szereg<br />
n=1<br />
∞∑<br />
ca n jest zbieżny oraz<br />
n=1<br />
∞∑<br />
∞∑<br />
ca n = c a n .<br />
n=1 n=1<br />
Szeregi
Szeregi <strong>liczbowe</strong><br />
Szeregi potęgowe<br />
Szeregi Fouriera<br />
Twierdzenie<br />
∑<br />
1. Jeżeli szereg ∞ a n jest zbieżny, to dla dowolnego c ∈ R szereg<br />
n=1<br />
∞∑<br />
ca n jest zbieżny oraz<br />
n=1<br />
∞∑<br />
∞∑<br />
ca n = c a n .<br />
n=1 n=1<br />
∞∑ ∞∑<br />
∑<br />
2. Jeżeli <strong>szeregi</strong> a n , b n są zbieżne, to szereg ∞ (a n + b n )<br />
n=1 n=1<br />
n=1<br />
jest zbieżny oraz<br />
∞∑<br />
∞∑ ∞∑<br />
(a n + b n ) = a n + b n .<br />
n=1<br />
n=1 n=1<br />
Szeregi
Szeregi <strong>liczbowe</strong><br />
Szeregi potęgowe<br />
Szeregi Fouriera<br />
Na ogół trudne jest wyznaczenie wzoru na sumę s n , a co za tym<br />
idzie wyznaczenie sumy szeregu S.<br />
Szeregi
Szeregi <strong>liczbowe</strong><br />
Szeregi potęgowe<br />
Szeregi Fouriera<br />
Na ogół trudne jest wyznaczenie wzoru na sumę s n , a co za tym<br />
idzie wyznaczenie sumy szeregu S.<br />
Zadanie łatwiejsze: zbadać tylko zbieżność szeregu.<br />
Szeregi
Szeregi <strong>liczbowe</strong><br />
Szeregi potęgowe<br />
Szeregi Fouriera<br />
Na ogół trudne jest wyznaczenie wzoru na sumę s n , a co za tym<br />
idzie wyznaczenie sumy szeregu S.<br />
Zadanie łatwiejsze: zbadać tylko zbieżność szeregu.<br />
Jeśli wiadomo, że szereg jest zbieżny, to można potem obliczać<br />
chociaż jego wartość przybliżoną (biorąc np. 100 czy 1000 wyrazów<br />
szeregu, zależnie od dokładności przybliżenia jaką chcemy<br />
osiągnąć).<br />
Szeregi
Szeregi <strong>liczbowe</strong><br />
Szeregi potęgowe<br />
Szeregi Fouriera<br />
Na ogół trudne jest wyznaczenie wzoru na sumę s n , a co za tym<br />
idzie wyznaczenie sumy szeregu S.<br />
Zadanie łatwiejsze: zbadać tylko zbieżność szeregu.<br />
Jeśli wiadomo, że szereg jest zbieżny, to można potem obliczać<br />
chociaż jego wartość przybliżoną (biorąc np. 100 czy 1000 wyrazów<br />
szeregu, zależnie od dokładności przybliżenia jaką chcemy<br />
osiągnąć).<br />
Twierdzenia podające warunki zbieżności szeregu nazywamy<br />
kryteriami zbieżności.<br />
Szeregi
Szeregi <strong>liczbowe</strong><br />
Szeregi potęgowe<br />
Szeregi Fouriera<br />
Kryteria zbieżności<br />
Twierdzenie (kryterium porównawcze)<br />
Jeżeli 0 a n b n dla n ∈ N, to<br />
∑<br />
1. Jeżeli szereg ∞ ∑<br />
b n jest zbieżny, to szereg ∞ a n jest zbieżny;<br />
n=1<br />
n=1<br />
Szeregi
Szeregi <strong>liczbowe</strong><br />
Szeregi potęgowe<br />
Szeregi Fouriera<br />
Kryteria zbieżności<br />
Twierdzenie (kryterium porównawcze)<br />
Jeżeli 0 a n b n dla n ∈ N, to<br />
∑<br />
1. Jeżeli szereg ∞ ∑<br />
b n jest zbieżny, to szereg ∞ a n jest zbieżny;<br />
n=1<br />
n=1<br />
∑<br />
2. Jeżeli szereg ∞ ∑<br />
a n jest rozbieżny, to szereg ∞ b n jest<br />
rozbieżny.<br />
n=1<br />
n=1<br />
Szeregi
Szeregi <strong>liczbowe</strong><br />
Szeregi potęgowe<br />
Szeregi Fouriera<br />
Kryteria zbieżności<br />
Twierdzenie (kryterium porównawcze)<br />
Jeżeli 0 a n b n dla n ∈ N, to<br />
∑<br />
1. Jeżeli szereg ∞ ∑<br />
b n jest zbieżny, to szereg ∞ a n jest zbieżny;<br />
n=1<br />
n=1<br />
∑<br />
2. Jeżeli szereg ∞ ∑<br />
a n jest rozbieżny, to szereg ∞ b n jest<br />
rozbieżny.<br />
n=1<br />
n=1<br />
Aby to twierdzenie stosować trzeba znać jakąś grupę szeregów<br />
zbieżnych bądź rozbieżnych.<br />
Szeregi
Szeregi <strong>liczbowe</strong><br />
Szeregi potęgowe<br />
Szeregi Fouriera<br />
Kryteria zbieżności<br />
Twierdzenie (kryterium porównawcze)<br />
Jeżeli 0 a n b n dla n ∈ N, to<br />
∑<br />
1. Jeżeli szereg ∞ ∑<br />
b n jest zbieżny, to szereg ∞ a n jest zbieżny;<br />
n=1<br />
n=1<br />
∑<br />
2. Jeżeli szereg ∞ ∑<br />
a n jest rozbieżny, to szereg ∞ b n jest<br />
rozbieżny.<br />
n=1<br />
n=1<br />
Aby to twierdzenie stosować trzeba znać jakąś grupę szeregów<br />
zbieżnych bądź rozbieżnych.<br />
Szereg postaci<br />
∞∑ 1<br />
n α<br />
n=1<br />
(tzw. szereg Dirichleta) jest zbieżny dla α > 1, a rozbieżny dla<br />
α 1.<br />
Szeregi
Szeregi <strong>liczbowe</strong><br />
Szeregi potęgowe<br />
Szeregi Fouriera<br />
Kryteria zbieżności<br />
Przykłady. Zbadać zbieżność szeregu:<br />
∞∑<br />
1.<br />
n=1<br />
sin 2 n<br />
n 2 ;<br />
Szeregi
Szeregi <strong>liczbowe</strong><br />
Szeregi potęgowe<br />
Szeregi Fouriera<br />
Kryteria zbieżności<br />
Przykłady. Zbadać zbieżność szeregu:<br />
∞∑<br />
1.<br />
n=1<br />
sin 2 n<br />
n 2 ;<br />
Ponieważ sin2 n<br />
n 2 1 n 2 oraz ∞ ∑<br />
n=1<br />
1<br />
n 2<br />
jest zbieżny,<br />
Szeregi
Szeregi <strong>liczbowe</strong><br />
Szeregi potęgowe<br />
Szeregi Fouriera<br />
Kryteria zbieżności<br />
Przykłady. Zbadać zbieżność szeregu:<br />
∞∑<br />
1.<br />
n=1<br />
sin 2 n<br />
n 2 ;<br />
Ponieważ sin2 n<br />
n 2 1 n 2 oraz ∞ ∑<br />
więc ∞ ∑<br />
n=1<br />
sin 2 n<br />
n 2<br />
n=1<br />
też jest zbieżny.<br />
1<br />
n 2<br />
jest zbieżny,<br />
Szeregi
Szeregi <strong>liczbowe</strong><br />
Szeregi potęgowe<br />
Szeregi Fouriera<br />
Kryteria zbieżności<br />
Przykłady. Zbadać zbieżność szeregu:<br />
∞∑<br />
1.<br />
n=1<br />
sin 2 n<br />
n 2 ;<br />
Ponieważ sin2 n<br />
n 2 1 n 2 oraz ∞ ∑<br />
więc ∞ ∑<br />
2.<br />
n=1<br />
∞∑<br />
n=1<br />
sin 2 n<br />
n 2<br />
√ 1<br />
; n(n+1)<br />
n=1<br />
też jest zbieżny.<br />
1<br />
n 2<br />
jest zbieżny,<br />
Szeregi
Szeregi <strong>liczbowe</strong><br />
Szeregi potęgowe<br />
Szeregi Fouriera<br />
Kryteria zbieżności<br />
Przykłady. Zbadać zbieżność szeregu:<br />
∞∑<br />
1.<br />
n=1<br />
sin 2 n<br />
n 2 ;<br />
Ponieważ sin2 n<br />
n 2 1 n 2 oraz ∞ ∑<br />
więc ∞ ∑<br />
2.<br />
n=1<br />
∞∑<br />
n=1<br />
sin 2 n<br />
n 2<br />
√ 1<br />
; n(n+1)<br />
n=1<br />
też jest zbieżny.<br />
1<br />
n 2<br />
√ 1<br />
√ 1<br />
= 1<br />
n(n+1) (n+1) 2 n+1 oraz ∑ ∞<br />
jest zbieżny,<br />
n=1<br />
1<br />
n+1<br />
szereg harmoniczny bez pierwszego wyrazu),<br />
jest rozbieżny (bo jest to<br />
Szeregi
Szeregi <strong>liczbowe</strong><br />
Szeregi potęgowe<br />
Szeregi Fouriera<br />
Kryteria zbieżności<br />
Przykłady. Zbadać zbieżność szeregu:<br />
∞∑<br />
1.<br />
n=1<br />
sin 2 n<br />
n 2 ;<br />
Ponieważ sin2 n<br />
n 2 1 n 2 oraz ∞ ∑<br />
więc ∞ ∑<br />
2.<br />
n=1<br />
∞∑<br />
n=1<br />
sin 2 n<br />
n 2<br />
√ 1<br />
; n(n+1)<br />
n=1<br />
też jest zbieżny.<br />
1<br />
n 2<br />
√ 1<br />
√ 1<br />
= 1<br />
n(n+1) (n+1) 2 n+1 oraz ∑ ∞<br />
jest zbieżny,<br />
n=1<br />
1<br />
n+1<br />
szereg harmoniczny bez pierwszego wyrazu),<br />
∑<br />
więc ∞ √ 1<br />
też jest rozbieżny.<br />
n(n+1)<br />
n=1<br />
jest rozbieżny (bo jest to<br />
Szeregi
Szeregi <strong>liczbowe</strong><br />
Szeregi potęgowe<br />
Szeregi Fouriera<br />
3.<br />
∞∑<br />
n=1<br />
3n+1<br />
n 2 −3 ;<br />
Szeregi
Szeregi <strong>liczbowe</strong><br />
Szeregi potęgowe<br />
Szeregi Fouriera<br />
3.<br />
4.<br />
∞∑<br />
n=1<br />
∞∑<br />
n=1<br />
3n+1<br />
n 2 −3 ;<br />
3n+1<br />
n 3 +3 .<br />
Szeregi
Szeregi <strong>liczbowe</strong><br />
Szeregi potęgowe<br />
Szeregi Fouriera<br />
Kryteria zbieżności<br />
Twierdzenie (kryterium ilorazowe)<br />
Jeżeli a n 0 i lim n→∞<br />
a n+1<br />
a n<br />
= q, to<br />
Szeregi
Szeregi <strong>liczbowe</strong><br />
Szeregi potęgowe<br />
Szeregi Fouriera<br />
Kryteria zbieżności<br />
Twierdzenie (kryterium ilorazowe)<br />
a<br />
Jeżeli a n 0 i lim n+1<br />
n→∞ a n<br />
= q, to<br />
∑<br />
1. jeżeli q < 1, to szereg ∞ a n jest zbieżny;<br />
n=1<br />
Szeregi
Szeregi <strong>liczbowe</strong><br />
Szeregi potęgowe<br />
Szeregi Fouriera<br />
Kryteria zbieżności<br />
Twierdzenie (kryterium ilorazowe)<br />
a<br />
Jeżeli a n 0 i lim n+1<br />
n→∞ a n<br />
= q, to<br />
∑<br />
1. jeżeli q < 1, to szereg ∞ a n jest zbieżny;<br />
n=1<br />
∑<br />
2. jeżeli q > 1, to szereg ∞ a n jest rozbieżny.<br />
n=1<br />
Szeregi
Szeregi <strong>liczbowe</strong><br />
Szeregi potęgowe<br />
Szeregi Fouriera<br />
Kryteria zbieżności<br />
Twierdzenie (kryterium ilorazowe)<br />
a<br />
Jeżeli a n 0 i lim n+1<br />
n→∞ a n<br />
= q, to<br />
∑<br />
1. jeżeli q < 1, to szereg ∞ a n jest zbieżny;<br />
n=1<br />
∑<br />
2. jeżeli q > 1, to szereg ∞ a n jest rozbieżny.<br />
n=1<br />
Kryterium ilorazowe nazywane jest też kryterium d’Alemberta. Nie<br />
rozstrzyga ono zbieżności, gdy q = 1, a takich przypadków jest<br />
wiele.<br />
Szeregi
Szeregi <strong>liczbowe</strong><br />
Szeregi potęgowe<br />
Szeregi Fouriera<br />
Kryteria zbieżności<br />
Twierdzenie (kryterium ilorazowe)<br />
a<br />
Jeżeli a n 0 i lim n+1<br />
n→∞ a n<br />
= q, to<br />
∑<br />
1. jeżeli q < 1, to szereg ∞ a n jest zbieżny;<br />
n=1<br />
∑<br />
2. jeżeli q > 1, to szereg ∞ a n jest rozbieżny.<br />
n=1<br />
Kryterium ilorazowe nazywane jest też kryterium d’Alemberta. Nie<br />
rozstrzyga ono zbieżności, gdy q = 1, a takich przypadków jest<br />
wiele. Np. dla szeregów<br />
∞∑<br />
n=1<br />
1<br />
n ,<br />
∞ ∑<br />
n=1<br />
1<br />
n 2<br />
otrzymamy q = 1.<br />
Szeregi
Szeregi <strong>liczbowe</strong><br />
Szeregi potęgowe<br />
Szeregi Fouriera<br />
Przykłady. Zbadać zbieżność szeregu:<br />
∞∑<br />
1.<br />
n=1<br />
n!<br />
n n ;<br />
Szeregi
Szeregi <strong>liczbowe</strong><br />
Szeregi potęgowe<br />
Szeregi Fouriera<br />
Przykłady. Zbadać zbieżność szeregu:<br />
∞∑<br />
1.<br />
2.<br />
n=1<br />
∞∑<br />
n=1<br />
n!<br />
n n ;<br />
1<br />
(2n)! .<br />
Szeregi
Szeregi <strong>liczbowe</strong><br />
Szeregi potęgowe<br />
Szeregi Fouriera<br />
Kryteria zbieżności<br />
Twierdzenie (kryterium pierwiastkowe)<br />
Jeżeli a n 0 i lim n→∞<br />
n √ a n = q, to<br />
Szeregi
Szeregi <strong>liczbowe</strong><br />
Szeregi potęgowe<br />
Szeregi Fouriera<br />
Kryteria zbieżności<br />
Twierdzenie (kryterium pierwiastkowe)<br />
Jeżeli a n 0 i lim √ n n→∞ a n = q, to<br />
∑<br />
1. jeżeli q < 1, to szereg ∞ a n jest zbieżny;<br />
n=1<br />
Szeregi
Szeregi <strong>liczbowe</strong><br />
Szeregi potęgowe<br />
Szeregi Fouriera<br />
Kryteria zbieżności<br />
Twierdzenie (kryterium pierwiastkowe)<br />
Jeżeli a n 0 i lim √ n n→∞ a n = q, to<br />
∑<br />
1. jeżeli q < 1, to szereg ∞ a n jest zbieżny;<br />
n=1<br />
∑<br />
2. jeżeli q > 1, to szereg ∞ a n jest rozbieżny.<br />
n=1<br />
Szeregi
Szeregi <strong>liczbowe</strong><br />
Szeregi potęgowe<br />
Szeregi Fouriera<br />
Kryteria zbieżności<br />
Twierdzenie (kryterium pierwiastkowe)<br />
Jeżeli a n 0 i lim √ n n→∞ a n = q, to<br />
∑<br />
1. jeżeli q < 1, to szereg ∞ a n jest zbieżny;<br />
n=1<br />
∑<br />
2. jeżeli q > 1, to szereg ∞ a n jest rozbieżny.<br />
n=1<br />
Inna nazwa: kryterium Cauchy’ego. Gdy q = 1, nie rozstrzyga ono<br />
zbieżności.<br />
Szeregi
Szeregi <strong>liczbowe</strong><br />
Szeregi potęgowe<br />
Szeregi Fouriera<br />
Kryteria zbieżności<br />
Twierdzenie (kryterium pierwiastkowe)<br />
Jeżeli a n 0 i lim √ n n→∞ a n = q, to<br />
∑<br />
1. jeżeli q < 1, to szereg ∞ a n jest zbieżny;<br />
n=1<br />
∑<br />
2. jeżeli q > 1, to szereg ∞ a n jest rozbieżny.<br />
n=1<br />
Inna nazwa: kryterium Cauchy’ego. Gdy q = 1, nie rozstrzyga ono<br />
zbieżności.<br />
Przykłady. Zbadać zbieżność szeregu:<br />
1.<br />
∞∑<br />
n=1<br />
( ) 3n+2 n;<br />
2n+3<br />
Szeregi
Szeregi <strong>liczbowe</strong><br />
Szeregi potęgowe<br />
Szeregi Fouriera<br />
Kryteria zbieżności<br />
Twierdzenie (kryterium pierwiastkowe)<br />
Jeżeli a n 0 i lim √ n n→∞ a n = q, to<br />
∑<br />
1. jeżeli q < 1, to szereg ∞ a n jest zbieżny;<br />
n=1<br />
∑<br />
2. jeżeli q > 1, to szereg ∞ a n jest rozbieżny.<br />
n=1<br />
Inna nazwa: kryterium Cauchy’ego. Gdy q = 1, nie rozstrzyga ono<br />
zbieżności.<br />
Przykłady. Zbadać zbieżność szeregu:<br />
1.<br />
∞∑<br />
n=1<br />
( 3n+2<br />
2n+3) n;<br />
2.<br />
∞∑<br />
n=2<br />
1<br />
(ln n) n .<br />
Szeregi
Szeregi <strong>liczbowe</strong><br />
Szeregi potęgowe<br />
Szeregi Fouriera<br />
Kryteria zbieżności<br />
Twierdzenie (kryterium całkowe)<br />
Niech funkcja f (x) będzie nieujemna i nierosnąca dla x ∈ [1, ∞).<br />
∑<br />
Wtedy szereg ∞ f (n) jest zbieżny wtedy i tylko wtedy, gdy całka<br />
niewłaściwa ∞ ∫<br />
1<br />
n=1<br />
f (x) dx jest zbieżna.<br />
Szeregi
Szeregi <strong>liczbowe</strong><br />
Szeregi potęgowe<br />
Szeregi Fouriera<br />
Kryteria zbieżności<br />
Twierdzenie (kryterium całkowe)<br />
Niech funkcja f (x) będzie nieujemna i nierosnąca dla x ∈ [1, ∞).<br />
∑<br />
Wtedy szereg ∞ f (n) jest zbieżny wtedy i tylko wtedy, gdy całka<br />
niewłaściwa ∞ ∫<br />
1<br />
n=1<br />
f (x) dx jest zbieżna.<br />
Przykłady. 1. Wykazać rozbieżność szeregu harmonicznego<br />
∫<br />
obliczając całkę ∞ 1<br />
x dx.<br />
1<br />
Szeregi
Szeregi <strong>liczbowe</strong><br />
Szeregi potęgowe<br />
Szeregi Fouriera<br />
Kryteria zbieżności<br />
Twierdzenie (kryterium całkowe)<br />
Niech funkcja f (x) będzie nieujemna i nierosnąca dla x ∈ [1, ∞).<br />
∑<br />
Wtedy szereg ∞ f (n) jest zbieżny wtedy i tylko wtedy, gdy całka<br />
niewłaściwa ∞ ∫<br />
1<br />
n=1<br />
f (x) dx jest zbieżna.<br />
Przykłady. 1. Wykazać rozbieżność szeregu harmonicznego<br />
∫<br />
obliczając całkę ∞ 1<br />
x dx.<br />
1<br />
2. Wykazać zbieżność szeregu ∞ ∑<br />
n=1<br />
1<br />
(n) α dla α > 1.<br />
Szeregi
Szeregi <strong>liczbowe</strong><br />
Szeregi potęgowe<br />
Szeregi Fouriera<br />
Kryteria zbieżności<br />
Wszystkie powyższe kryteria zakładały nieujemność wyrazów<br />
szeregu.<br />
Szeregi
Szeregi <strong>liczbowe</strong><br />
Szeregi potęgowe<br />
Szeregi Fouriera<br />
Kryteria zbieżności<br />
Wszystkie powyższe kryteria zakładały nieujemność wyrazów<br />
szeregu.<br />
Definicja<br />
∑<br />
Szereg ∞ a n nazywamy bezwzględnie zbieżnym, gdy szereg<br />
n=1<br />
∞∑<br />
|a n | utworzony z jego wartości bezwzględnych jest zbieżny.<br />
n=1<br />
Szeregi
Szeregi <strong>liczbowe</strong><br />
Szeregi potęgowe<br />
Szeregi Fouriera<br />
Kryteria zbieżności<br />
Wszystkie powyższe kryteria zakładały nieujemność wyrazów<br />
szeregu.<br />
Definicja<br />
∑<br />
Szereg ∞ a n nazywamy bezwzględnie zbieżnym, gdy szereg<br />
n=1<br />
∞∑<br />
|a n | utworzony z jego wartości bezwzględnych jest zbieżny.<br />
n=1<br />
Szereg zbieżny, ale nie bezwzględnie zbieżny, nazywamy<br />
warunkowo zbieżnym.<br />
Szeregi
Szeregi <strong>liczbowe</strong><br />
Szeregi potęgowe<br />
Szeregi Fouriera<br />
Kryteria zbieżności<br />
Wszystkie powyższe kryteria zakładały nieujemność wyrazów<br />
szeregu.<br />
Definicja<br />
∑<br />
Szereg ∞ a n nazywamy bezwzględnie zbieżnym, gdy szereg<br />
n=1<br />
∞∑<br />
|a n | utworzony z jego wartości bezwzględnych jest zbieżny.<br />
n=1<br />
Szereg zbieżny, ale nie bezwzględnie zbieżny, nazywamy<br />
warunkowo zbieżnym.<br />
∞∑<br />
Jeżeli a n jest bezwzględnie zbieżny, to jest zbieżny.<br />
n=1<br />
Szeregi
Szeregi <strong>liczbowe</strong><br />
Szeregi potęgowe<br />
Szeregi Fouriera<br />
Przy badaniu zbieżności szeregu najpierw należy wyjaśnić, czy<br />
szereg jest bezwzględnie zbieżny. Mamy tu do dyspozycji cztery<br />
wymienione wyżej kryteria zbieżności.<br />
Szeregi
Szeregi <strong>liczbowe</strong><br />
Szeregi potęgowe<br />
Szeregi Fouriera<br />
Przy badaniu zbieżności szeregu najpierw należy wyjaśnić, czy<br />
szereg jest bezwzględnie zbieżny. Mamy tu do dyspozycji cztery<br />
wymienione wyżej kryteria zbieżności.<br />
Jeśli okaże się, że szereg nie jest bezwzględnie zbieżny, to powstaje<br />
problem zbadania zbieżności warunkowej.<br />
Szeregi
Szeregi <strong>liczbowe</strong><br />
Szeregi potęgowe<br />
Szeregi Fouriera<br />
Kryteria zbieżności<br />
Definicja<br />
Szereg postaci<br />
∞∑<br />
(−1) n−1 a n = a 1 − a 2 + a 3 − a 4 + · · ·<br />
n=1<br />
gdzie a n 0 nazywamy naprzemiennym.<br />
Szeregi
Szeregi <strong>liczbowe</strong><br />
Szeregi potęgowe<br />
Szeregi Fouriera<br />
Kryteria zbieżności<br />
Definicja<br />
Szereg postaci<br />
∞∑<br />
(−1) n−1 a n = a 1 − a 2 + a 3 − a 4 + · · ·<br />
n=1<br />
gdzie a n 0 nazywamy naprzemiennym.<br />
Takim <strong>szeregi</strong>em jest np. szereg anharmoniczny.<br />
∞∑<br />
(−1) n−1 1 n = 1 − 1 2 + 1 3 − 1 4 + · · ·<br />
n=1<br />
Szeregi
Szeregi <strong>liczbowe</strong><br />
Szeregi potęgowe<br />
Szeregi Fouriera<br />
Twierdzenie (kryterium Leibniza)<br />
Jeśli ciąg a n jest nieujemny, nierosnący i dąży do 0, to<br />
∞∑<br />
(−1) n−1 a n jest zbieżny.<br />
n=1<br />
Szeregi
Szeregi <strong>liczbowe</strong><br />
Szeregi potęgowe<br />
Szeregi Fouriera<br />
Kryteria zbieżności<br />
Przykłady.<br />
1. Ciąg 1 n<br />
jest nieujemny, nierosnący i dąży do 0.<br />
Szeregi
Szeregi <strong>liczbowe</strong><br />
Szeregi potęgowe<br />
Szeregi Fouriera<br />
Kryteria zbieżności<br />
Przykłady.<br />
1. Ciąg 1 n<br />
jest nieujemny, nierosnący i dąży do 0.<br />
Zatem szereg anharmoniczny jest zbieżny, ale tylko warunkowo, bo<br />
utworzony z jego wartości bezwzględnych szereg harmoniczny jest<br />
rozbieżny.<br />
Szeregi
Szeregi <strong>liczbowe</strong><br />
Szeregi potęgowe<br />
Szeregi Fouriera<br />
Kryteria zbieżności<br />
Przykłady.<br />
1. Ciąg 1 n<br />
jest nieujemny, nierosnący i dąży do 0.<br />
Zatem szereg anharmoniczny jest zbieżny, ale tylko warunkowo, bo<br />
utworzony z jego wartości bezwzględnych szereg harmoniczny jest<br />
rozbieżny.<br />
∞∑<br />
2. (−1)<br />
n−1 ln n. (warunkowo zbieżny)<br />
n=1<br />
n<br />
Szeregi
Szeregi <strong>liczbowe</strong><br />
Szeregi potęgowe<br />
Szeregi Fouriera<br />
Kryteria zbieżności<br />
Przykłady.<br />
1. Ciąg 1 n<br />
jest nieujemny, nierosnący i dąży do 0.<br />
Zatem szereg anharmoniczny jest zbieżny, ale tylko warunkowo, bo<br />
utworzony z jego wartości bezwzględnych szereg harmoniczny jest<br />
rozbieżny.<br />
∞∑<br />
2. (−1)<br />
n−1 ln n. (warunkowo zbieżny)<br />
3.<br />
n=1<br />
∞∑<br />
n=1<br />
n<br />
(−1) n−1<br />
√ n+1+<br />
√ n<br />
. (warunkowo zbieżny)<br />
Szeregi
Szeregi <strong>liczbowe</strong><br />
Szeregi potęgowe<br />
Szeregi Fouriera<br />
Kryteria zbieżności<br />
Przykłady.<br />
1. Ciąg 1 n<br />
jest nieujemny, nierosnący i dąży do 0.<br />
Zatem szereg anharmoniczny jest zbieżny, ale tylko warunkowo, bo<br />
utworzony z jego wartości bezwzględnych szereg harmoniczny jest<br />
rozbieżny.<br />
∞∑<br />
2. (−1)<br />
n−1 ln n. (warunkowo zbieżny)<br />
3.<br />
4.<br />
n=1<br />
∞∑<br />
n=1<br />
∞∑<br />
n=1<br />
spełniony)<br />
n<br />
(−1) n−1<br />
√ n+1+<br />
√ n<br />
. (warunkowo zbieżny)<br />
(−1) n−1<br />
√ n+1−<br />
√ n<br />
. (rozbieżny — warunek konieczny nie jest<br />
Szeregi
Szeregi <strong>liczbowe</strong><br />
Szeregi potęgowe<br />
Szeregi Fouriera<br />
Kryteria zbieżności<br />
Przykłady.<br />
1. Ciąg 1 n<br />
jest nieujemny, nierosnący i dąży do 0.<br />
Zatem szereg anharmoniczny jest zbieżny, ale tylko warunkowo, bo<br />
utworzony z jego wartości bezwzględnych szereg harmoniczny jest<br />
rozbieżny.<br />
∞∑<br />
2. (−1)<br />
n−1 ln n. (warunkowo zbieżny)<br />
3.<br />
4.<br />
n=1<br />
∞∑<br />
n=1<br />
∞∑<br />
n=1<br />
n<br />
(−1) n−1<br />
√ n+1+<br />
√ n<br />
. (warunkowo zbieżny)<br />
(−1) n−1<br />
√ n+1−<br />
√ n<br />
. (rozbieżny — warunek konieczny nie jest<br />
spełniony)<br />
∞∑ (−1)<br />
5.<br />
n−1<br />
. (bezwzględnie zbieżny)<br />
n 2<br />
n=1<br />
Szeregi
Szeregi funkcyjne<br />
Szeregi <strong>liczbowe</strong><br />
Szeregi potęgowe<br />
Szeregi Fouriera<br />
Szereg postaci<br />
∞∑<br />
f n (x)<br />
n=1<br />
którego wyrazy są funkcjami zmiennej x, określone w tej samej<br />
dziedzinie D, nazywamy <strong>szeregi</strong>em funkcyjnym.<br />
Szeregi
Szeregi funkcyjne<br />
Szeregi <strong>liczbowe</strong><br />
Szeregi potęgowe<br />
Szeregi Fouriera<br />
Szereg postaci<br />
∞∑<br />
f n (x)<br />
n=1<br />
którego wyrazy są funkcjami zmiennej x, określone w tej samej<br />
dziedzinie D, nazywamy <strong>szeregi</strong>em funkcyjnym.<br />
Dla ustalonego x ∈ D szereg może być zbieżny lub nie.<br />
Szeregi
Szeregi funkcyjne<br />
Szeregi <strong>liczbowe</strong><br />
Szeregi potęgowe<br />
Szeregi Fouriera<br />
Szereg postaci<br />
∞∑<br />
f n (x)<br />
n=1<br />
którego wyrazy są funkcjami zmiennej x, określone w tej samej<br />
dziedzinie D, nazywamy <strong>szeregi</strong>em funkcyjnym.<br />
Dla ustalonego x ∈ D szereg może być zbieżny lub nie.<br />
Zbiór wszystkich x ∈ D dla których szereg jest zbieżny nazywamy<br />
obszarem zbieżności szeregu.<br />
Szeregi
Szeregi funkcyjne<br />
Szeregi <strong>liczbowe</strong><br />
Szeregi potęgowe<br />
Szeregi Fouriera<br />
Szereg postaci<br />
∞∑<br />
f n (x)<br />
n=1<br />
którego wyrazy są funkcjami zmiennej x, określone w tej samej<br />
dziedzinie D, nazywamy <strong>szeregi</strong>em funkcyjnym.<br />
Dla ustalonego x ∈ D szereg może być zbieżny lub nie.<br />
Zbiór wszystkich x ∈ D dla których szereg jest zbieżny nazywamy<br />
obszarem zbieżności szeregu.<br />
Obszar ten może być zbiorem pustym.<br />
Szeregi
Szeregi <strong>liczbowe</strong><br />
Szeregi potęgowe<br />
Szeregi Fouriera<br />
Np. dla szeregu<br />
∞∑<br />
n=1<br />
1<br />
n x<br />
obszarem zbieżności jest przedział (1, ∞),<br />
Szeregi
Szeregi <strong>liczbowe</strong><br />
Szeregi potęgowe<br />
Szeregi Fouriera<br />
Np. dla szeregu<br />
∞∑<br />
n=1<br />
1<br />
n x<br />
obszarem zbieżności jest przedział (1, ∞),<br />
a dla szeregu<br />
∞∑<br />
x n<br />
n=1<br />
Szeregi
Szeregi <strong>liczbowe</strong><br />
Szeregi potęgowe<br />
Szeregi Fouriera<br />
Np. dla szeregu<br />
∞∑<br />
n=1<br />
1<br />
n x<br />
obszarem zbieżności jest przedział (1, ∞),<br />
a dla szeregu<br />
∞∑<br />
x n<br />
n=1<br />
obszarem zbieżności jest przedział (−1, 1).<br />
Szeregi
Szeregi potęgowe<br />
Szeregi <strong>liczbowe</strong><br />
Szeregi potęgowe<br />
Szeregi Fouriera<br />
Definicja<br />
Szereg postaci<br />
∞∑<br />
a n (x − x 0 ) n , (3)<br />
n=0<br />
nazywamy <strong>szeregi</strong>em potęgowym.<br />
Szeregi
Szeregi potęgowe<br />
Szeregi <strong>liczbowe</strong><br />
Szeregi potęgowe<br />
Szeregi Fouriera<br />
Definicja<br />
Szereg postaci<br />
∞∑<br />
a n (x − x 0 ) n , (3)<br />
n=0<br />
nazywamy <strong>szeregi</strong>em potęgowym.<br />
∑<br />
Dla x 0 = 0 mamy szereg ∞ a n x n .<br />
n=0<br />
Szeregi
Szeregi potęgowe<br />
Szeregi <strong>liczbowe</strong><br />
Szeregi potęgowe<br />
Szeregi Fouriera<br />
Twierdzenie (o obszarze zbieżności szeregu potęgowego)<br />
Jeśli R jest liczbą wyznaczoną ze wzoru<br />
|a n |<br />
R = lim<br />
n→∞ |a n+1 | , (4)<br />
Szeregi
Szeregi potęgowe<br />
Szeregi <strong>liczbowe</strong><br />
Szeregi potęgowe<br />
Szeregi Fouriera<br />
Twierdzenie (o obszarze zbieżności szeregu potęgowego)<br />
Jeśli R jest liczbą wyznaczoną ze wzoru<br />
|a n |<br />
R = lim<br />
n→∞ |a n+1 | , (4)<br />
lub ze wzoru<br />
R = lim<br />
n→∞<br />
1<br />
√<br />
|an | , (5)<br />
n<br />
Szeregi
Szeregi potęgowe<br />
Szeregi <strong>liczbowe</strong><br />
Szeregi potęgowe<br />
Szeregi Fouriera<br />
Twierdzenie (o obszarze zbieżności szeregu potęgowego)<br />
Jeśli R jest liczbą wyznaczoną ze wzoru<br />
|a n |<br />
R = lim<br />
n→∞ |a n+1 | , (4)<br />
lub ze wzoru<br />
R = lim<br />
n→∞<br />
1<br />
√<br />
|an | , (5)<br />
n<br />
to szereg (3) jest zbieżny w przedziale (x 0 − R, x 0 + R) i rozbieżny<br />
w przedziałach (−∞, x 0 − R), (x 0 + R, ∞).<br />
Szeregi
Szeregi potęgowe<br />
Szeregi <strong>liczbowe</strong><br />
Szeregi potęgowe<br />
Szeregi Fouriera<br />
Twierdzenie (o obszarze zbieżności szeregu potęgowego)<br />
Jeśli R jest liczbą wyznaczoną ze wzoru<br />
|a n |<br />
R = lim<br />
n→∞ |a n+1 | , (4)<br />
lub ze wzoru<br />
R = lim<br />
n→∞<br />
1<br />
√<br />
|an | , (5)<br />
n<br />
to szereg (3) jest zbieżny w przedziale (x 0 − R, x 0 + R) i rozbieżny<br />
w przedziałach (−∞, x 0 − R), (x 0 + R, ∞).<br />
W punktach x 0 − R, x 0 + R szereg może być zbieżny lub nie.<br />
Szeregi
Szeregi potęgowe<br />
Szeregi <strong>liczbowe</strong><br />
Szeregi potęgowe<br />
Szeregi Fouriera<br />
Określoną wyżej liczbę R nazywamy promieniem zbieżności<br />
szeregu, a przedział (x 0 − R, x 0 + R) — przedziałem zbieżności.<br />
Szeregi
Szeregi potęgowe<br />
Szeregi <strong>liczbowe</strong><br />
Szeregi potęgowe<br />
Szeregi Fouriera<br />
Określoną wyżej liczbę R nazywamy promieniem zbieżności<br />
szeregu, a przedział (x 0 − R, x 0 + R) — przedziałem zbieżności.<br />
Przykłady. Zbadać zbieżność szeregów:<br />
1.<br />
∞∑<br />
n=1<br />
x n<br />
n3 n .<br />
Szeregi
Szeregi potęgowe<br />
Szeregi <strong>liczbowe</strong><br />
Szeregi potęgowe<br />
Szeregi Fouriera<br />
Określoną wyżej liczbę R nazywamy promieniem zbieżności<br />
szeregu, a przedział (x 0 − R, x 0 + R) — przedziałem zbieżności.<br />
Przykłady. Zbadać zbieżność szeregów:<br />
1.<br />
∞∑<br />
n=1<br />
x n<br />
n3 n .<br />
Tutaj a n = 1<br />
n3 n . Obliczamy<br />
R = lim<br />
n→∞<br />
1<br />
n3 n<br />
1<br />
(n+1)3 n+1 =<br />
Szeregi
Szeregi potęgowe<br />
Szeregi <strong>liczbowe</strong><br />
Szeregi potęgowe<br />
Szeregi Fouriera<br />
Określoną wyżej liczbę R nazywamy promieniem zbieżności<br />
szeregu, a przedział (x 0 − R, x 0 + R) — przedziałem zbieżności.<br />
Przykłady. Zbadać zbieżność szeregów:<br />
1.<br />
∞∑<br />
n=1<br />
x n<br />
n3 n .<br />
Tutaj a n = 1<br />
n3 n . Obliczamy<br />
R = lim<br />
n→∞<br />
1<br />
n3 n<br />
(n + 1)3 n+1<br />
1<br />
= lim<br />
n→∞ n3<br />
(n+1)3 n =<br />
n+1<br />
Szeregi
Szeregi potęgowe<br />
Szeregi <strong>liczbowe</strong><br />
Szeregi potęgowe<br />
Szeregi Fouriera<br />
Określoną wyżej liczbę R nazywamy promieniem zbieżności<br />
szeregu, a przedział (x 0 − R, x 0 + R) — przedziałem zbieżności.<br />
Przykłady. Zbadać zbieżność szeregów:<br />
1.<br />
∞∑<br />
n=1<br />
x n<br />
n3 n .<br />
Tutaj a n = 1<br />
n3 n . Obliczamy<br />
R = lim<br />
n→∞<br />
1<br />
n3 n<br />
(n + 1)3 n+1<br />
1<br />
= lim<br />
n→∞ n3<br />
(n+1)3 n<br />
n+1<br />
n + 1<br />
= 3 lim = 3,<br />
n→∞ n<br />
Szeregi
Szeregi potęgowe<br />
Szeregi <strong>liczbowe</strong><br />
Szeregi potęgowe<br />
Szeregi Fouriera<br />
Określoną wyżej liczbę R nazywamy promieniem zbieżności<br />
szeregu, a przedział (x 0 − R, x 0 + R) — przedziałem zbieżności.<br />
Przykłady. Zbadać zbieżność szeregów:<br />
1.<br />
∞∑<br />
n=1<br />
x n<br />
n3 n .<br />
Tutaj a n = 1<br />
n3 n . Obliczamy<br />
R = lim<br />
n→∞<br />
1<br />
n3 n<br />
(n + 1)3 n+1<br />
1<br />
= lim<br />
n→∞ n3<br />
(n+1)3 n<br />
n+1<br />
Zatem szereg jest na pewno zbieżny w (−3, 3).<br />
n + 1<br />
= 3 lim = 3,<br />
n→∞ n<br />
Szeregi
Szeregi potęgowe<br />
Szeregi <strong>liczbowe</strong><br />
Szeregi potęgowe<br />
Szeregi Fouriera<br />
Określoną wyżej liczbę R nazywamy promieniem zbieżności<br />
szeregu, a przedział (x 0 − R, x 0 + R) — przedziałem zbieżności.<br />
Przykłady. Zbadać zbieżność szeregów:<br />
1.<br />
∞∑<br />
n=1<br />
x n<br />
n3 n .<br />
Tutaj a n = 1<br />
n3 n . Obliczamy<br />
R = lim<br />
n→∞<br />
1<br />
n3 n<br />
(n + 1)3 n+1<br />
1<br />
= lim<br />
n→∞ n3<br />
(n+1)3 n<br />
n+1<br />
Zatem szereg jest na pewno zbieżny w (−3, 3).<br />
Dla x = 3 otrzymujemy szereg harmoniczny ∞ ∑<br />
rozbieżny,<br />
n + 1<br />
= 3 lim = 3,<br />
n→∞ n<br />
n=1<br />
1<br />
n<br />
, który jest<br />
Szeregi
Szeregi potęgowe<br />
Szeregi <strong>liczbowe</strong><br />
Szeregi potęgowe<br />
Szeregi Fouriera<br />
Określoną wyżej liczbę R nazywamy promieniem zbieżności<br />
szeregu, a przedział (x 0 − R, x 0 + R) — przedziałem zbieżności.<br />
Przykłady. Zbadać zbieżność szeregów:<br />
1.<br />
∞∑<br />
n=1<br />
x n<br />
n3 n .<br />
Tutaj a n = 1<br />
n3 n . Obliczamy<br />
R = lim<br />
n→∞<br />
1<br />
n3 n<br />
(n + 1)3 n+1<br />
1<br />
= lim<br />
n→∞ n3<br />
(n+1)3 n<br />
n+1<br />
Zatem szereg jest na pewno zbieżny w (−3, 3).<br />
Dla x = 3 otrzymujemy szereg harmoniczny ∞ ∑<br />
n + 1<br />
= 3 lim = 3,<br />
n→∞ n<br />
n=1<br />
1<br />
n<br />
, który jest<br />
rozbieżny,<br />
∑<br />
a dla x = −3 szereg anharmoniczny ∞ (−1) n−1 1 n , warunkowo<br />
zbieżny.<br />
n=1<br />
Szeregi
Szeregi <strong>liczbowe</strong><br />
Szeregi potęgowe<br />
Szeregi Fouriera<br />
Ostatecznie przedziałem zbieżności jest [−3, 3).<br />
Szeregi
Szeregi <strong>liczbowe</strong><br />
Szeregi potęgowe<br />
Szeregi Fouriera<br />
Ostatecznie przedziałem zbieżności jest [−3, 3).<br />
∞∑ x<br />
2. √ n<br />
n<br />
.<br />
n=1<br />
Teraz a n = √ 1<br />
n<br />
, więc<br />
Szeregi
Szeregi <strong>liczbowe</strong><br />
Szeregi potęgowe<br />
Szeregi Fouriera<br />
Ostatecznie przedziałem zbieżności jest [−3, 3).<br />
∞∑ x<br />
2. √ n<br />
n<br />
.<br />
n=1<br />
Teraz a n = √ 1<br />
n<br />
, więc<br />
R = lim<br />
n→∞<br />
√1<br />
n<br />
√ 1<br />
=<br />
n+1<br />
Szeregi
Szeregi <strong>liczbowe</strong><br />
Szeregi potęgowe<br />
Szeregi Fouriera<br />
Ostatecznie przedziałem zbieżności jest [−3, 3).<br />
∞∑ x<br />
2. √ n<br />
n<br />
.<br />
n=1<br />
Teraz a n = √ 1<br />
n<br />
, więc<br />
R = lim<br />
n→∞<br />
√1<br />
n<br />
√ 1<br />
=<br />
n+1<br />
√ n + 1<br />
lim √ =<br />
n→∞ n<br />
Szeregi
Szeregi <strong>liczbowe</strong><br />
Szeregi potęgowe<br />
Szeregi Fouriera<br />
Ostatecznie przedziałem zbieżności jest [−3, 3).<br />
∞∑ x<br />
2. √ n<br />
n<br />
.<br />
n=1<br />
Teraz a n = √ 1<br />
n<br />
, więc<br />
R = lim<br />
n→∞<br />
√1<br />
n<br />
√ 1<br />
=<br />
n+1<br />
√ n + 1<br />
lim √ = 1.<br />
n→∞ n<br />
Szeregi
Szeregi <strong>liczbowe</strong><br />
Szeregi potęgowe<br />
Szeregi Fouriera<br />
Ostatecznie przedziałem zbieżności jest [−3, 3).<br />
∞∑ x<br />
2. √ n<br />
n<br />
.<br />
n=1<br />
Teraz a n = √ 1<br />
n<br />
, więc<br />
R = lim<br />
n→∞<br />
Przedział zbieżności [−1, 1).<br />
√1<br />
n<br />
√ 1<br />
=<br />
n+1<br />
√ n + 1<br />
lim √ = 1.<br />
n→∞ n<br />
Szeregi
Szeregi <strong>liczbowe</strong><br />
Szeregi potęgowe<br />
Szeregi Fouriera<br />
Ostatecznie przedziałem zbieżności jest [−3, 3).<br />
∞∑ x<br />
2. √ n<br />
n<br />
.<br />
n=1<br />
Teraz a n = √ 1<br />
n<br />
, więc<br />
R = lim<br />
n→∞<br />
√1<br />
n<br />
√ 1<br />
=<br />
n+1<br />
√ n + 1<br />
lim √ = 1.<br />
n→∞ n<br />
Przedział zbieżności [−1, 1).<br />
W następnym przykładzie ograniczymy się do promienia zbieżności.<br />
∞∑ (n!)<br />
3.<br />
2<br />
(2n)! x n .<br />
n=0<br />
Szeregi
Szeregi <strong>liczbowe</strong><br />
Szeregi potęgowe<br />
Szeregi Fouriera<br />
Ostatecznie przedziałem zbieżności jest [−3, 3).<br />
∞∑ x<br />
2. √ n<br />
n<br />
.<br />
n=1<br />
Teraz a n = √ 1<br />
n<br />
, więc<br />
R = lim<br />
n→∞<br />
√1<br />
n<br />
√ 1<br />
=<br />
n+1<br />
√ n + 1<br />
lim √ = 1.<br />
n→∞ n<br />
Przedział zbieżności [−1, 1).<br />
W następnym przykładzie ograniczymy się do promienia zbieżności.<br />
∞∑ (n!)<br />
3.<br />
2<br />
(2n)! x n .<br />
n=0<br />
R = lim<br />
n→∞<br />
|a n |<br />
|a n+1 | = Szeregi
Szeregi <strong>liczbowe</strong><br />
Szeregi potęgowe<br />
Szeregi Fouriera<br />
Ostatecznie przedziałem zbieżności jest [−3, 3).<br />
∞∑ x<br />
2. √ n<br />
n<br />
.<br />
n=1<br />
Teraz a n = √ 1<br />
n<br />
, więc<br />
R = lim<br />
n→∞<br />
√1<br />
n<br />
√ 1<br />
=<br />
n+1<br />
√ n + 1<br />
lim √ = 1.<br />
n→∞ n<br />
Przedział zbieżności [−1, 1).<br />
W następnym przykładzie ograniczymy się do promienia zbieżności.<br />
∞∑ (n!)<br />
3.<br />
2<br />
(2n)! x n .<br />
n=0<br />
|a n |<br />
R = lim<br />
n→∞ |a n+1 | = lim (n!) 2 [2(n + 1)]!<br />
n→∞ (2n)![(n + 1)!] 2 =<br />
Szeregi
Szeregi <strong>liczbowe</strong><br />
Szeregi potęgowe<br />
Szeregi Fouriera<br />
Ostatecznie przedziałem zbieżności jest [−3, 3).<br />
∞∑ x<br />
2. √ n<br />
n<br />
.<br />
n=1<br />
Teraz a n = √ 1<br />
n<br />
, więc<br />
R = lim<br />
n→∞<br />
√1<br />
n<br />
√ 1<br />
=<br />
n+1<br />
√ n + 1<br />
lim √ = 1.<br />
n→∞ n<br />
Przedział zbieżności [−1, 1).<br />
W następnym przykładzie ograniczymy się do promienia zbieżności.<br />
∞∑ (n!)<br />
3.<br />
2<br />
(2n)! x n .<br />
n=0<br />
R = lim<br />
n→∞<br />
= lim<br />
n→∞<br />
|a n |<br />
|a n+1 | = lim n→∞<br />
(2n + 1)(2n + 2)<br />
(n + 1) 2 =<br />
(n!) 2 [2(n + 1)]!<br />
(2n)![(n + 1)!] 2 =<br />
Szeregi
Szeregi <strong>liczbowe</strong><br />
Szeregi potęgowe<br />
Szeregi Fouriera<br />
Ostatecznie przedziałem zbieżności jest [−3, 3).<br />
∞∑ x<br />
2. √ n<br />
n<br />
.<br />
n=1<br />
Teraz a n = √ 1<br />
n<br />
, więc<br />
R = lim<br />
n→∞<br />
√1<br />
n<br />
√ 1<br />
=<br />
n+1<br />
√ n + 1<br />
lim √ = 1.<br />
n→∞ n<br />
Przedział zbieżności [−1, 1).<br />
W następnym przykładzie ograniczymy się do promienia zbieżności.<br />
∞∑ (n!)<br />
3.<br />
2<br />
(2n)! x n .<br />
n=0<br />
R = lim<br />
n→∞<br />
= lim<br />
n→∞<br />
|a n |<br />
|a n+1 | = lim n→∞<br />
(n!) 2 [2(n + 1)]!<br />
(2n)![(n + 1)!] 2 =<br />
(2n + 1)(2n + 2)<br />
(n + 1) 2 = lim<br />
n→∞<br />
4n + 2<br />
n + 1 =<br />
Szeregi
Szeregi <strong>liczbowe</strong><br />
Szeregi potęgowe<br />
Szeregi Fouriera<br />
Ostatecznie przedziałem zbieżności jest [−3, 3).<br />
∞∑ x<br />
2. √ n<br />
n<br />
.<br />
n=1<br />
Teraz a n = √ 1<br />
n<br />
, więc<br />
R = lim<br />
n→∞<br />
√1<br />
n<br />
√ 1<br />
=<br />
n+1<br />
√ n + 1<br />
lim √ = 1.<br />
n→∞ n<br />
Przedział zbieżności [−1, 1).<br />
W następnym przykładzie ograniczymy się do promienia zbieżności.<br />
∞∑ (n!)<br />
3.<br />
2<br />
(2n)! x n .<br />
n=0<br />
R = lim<br />
n→∞<br />
= lim<br />
n→∞<br />
|a n |<br />
|a n+1 | = lim n→∞<br />
(n!) 2 [2(n + 1)]!<br />
(2n)![(n + 1)!] 2 =<br />
(2n + 1)(2n + 2)<br />
(n + 1) 2 = lim<br />
n→∞<br />
4n + 2<br />
n + 1 = 4.<br />
Szeregi
Szeregi <strong>liczbowe</strong><br />
Szeregi potęgowe<br />
Szeregi Fouriera<br />
Podstawowym zagadnieniem jest przedstawienie danej funkcji w<br />
postaci szeregu potęgowego.<br />
Szeregi
Szeregi <strong>liczbowe</strong><br />
Szeregi potęgowe<br />
Szeregi Fouriera<br />
Podstawowym zagadnieniem jest przedstawienie danej funkcji w<br />
postaci szeregu potęgowego.<br />
Definicja<br />
Załóżmy, że funkcja f ma w punkcie x 0 pochodne dowolnego<br />
rzędu. Można wtedy utworzyć szereg<br />
∞∑<br />
n=0<br />
f (n) (x 0 )<br />
n!<br />
(x−x 0 ) n = f (x 0 )+ f ′ (x 0 )<br />
1!<br />
(x−x 0 )+ f ′′ (x 0 )<br />
(x−x 0 ) 2 +· · · ,<br />
2!<br />
Szeregi
Szeregi <strong>liczbowe</strong><br />
Szeregi potęgowe<br />
Szeregi Fouriera<br />
Podstawowym zagadnieniem jest przedstawienie danej funkcji w<br />
postaci szeregu potęgowego.<br />
Definicja<br />
Załóżmy, że funkcja f ma w punkcie x 0 pochodne dowolnego<br />
rzędu. Można wtedy utworzyć szereg<br />
∞∑<br />
n=0<br />
f (n) (x 0 )<br />
n!<br />
(x−x 0 ) n = f (x 0 )+ f ′ (x 0 )<br />
1!<br />
(x−x 0 )+ f ′′ (x 0 )<br />
(x−x 0 ) 2 +· · · ,<br />
2!<br />
który nazywamy <strong>szeregi</strong>em Taylora funkcji f o środku w punkcie<br />
x 0 .<br />
Szeregi
Szeregi <strong>liczbowe</strong><br />
Szeregi potęgowe<br />
Szeregi Fouriera<br />
Podstawowym zagadnieniem jest przedstawienie danej funkcji w<br />
postaci szeregu potęgowego.<br />
Definicja<br />
Załóżmy, że funkcja f ma w punkcie x 0 pochodne dowolnego<br />
rzędu. Można wtedy utworzyć szereg<br />
∞∑<br />
n=0<br />
f (n) (x 0 )<br />
n!<br />
(x−x 0 ) n = f (x 0 )+ f ′ (x 0 )<br />
1!<br />
(x−x 0 )+ f ′′ (x 0 )<br />
(x−x 0 ) 2 +· · · ,<br />
2!<br />
który nazywamy <strong>szeregi</strong>em Taylora funkcji f o środku w punkcie<br />
x 0 .<br />
Jeżeli x 0 = 0, to ten szereg nazywamy <strong>szeregi</strong>em Maclaurina<br />
funkcji f .<br />
Szeregi
Szeregi <strong>liczbowe</strong><br />
Szeregi potęgowe<br />
Szeregi Fouriera<br />
Podstawowym zagadnieniem jest przedstawienie danej funkcji w<br />
postaci szeregu potęgowego.<br />
Definicja<br />
Załóżmy, że funkcja f ma w punkcie x 0 pochodne dowolnego<br />
rzędu. Można wtedy utworzyć szereg<br />
∞∑<br />
n=0<br />
f (n) (x 0 )<br />
n!<br />
(x−x 0 ) n = f (x 0 )+ f ′ (x 0 )<br />
1!<br />
(x−x 0 )+ f ′′ (x 0 )<br />
(x−x 0 ) 2 +· · · ,<br />
2!<br />
który nazywamy <strong>szeregi</strong>em Taylora funkcji f o środku w punkcie<br />
x 0 .<br />
Jeżeli x 0 = 0, to ten szereg nazywamy <strong>szeregi</strong>em Maclaurina<br />
funkcji f .<br />
Zatem pod warunkiem, że funkcja ma wszystkie pochodne można<br />
utworzyć pewien szereg z nią związany.<br />
Szeregi
Szeregi <strong>liczbowe</strong><br />
Szeregi potęgowe<br />
Szeregi Fouriera<br />
Ale:<br />
szereg nie musi być zbieżny w całej dziedzinie tej funkcji;<br />
Szeregi
Szeregi <strong>liczbowe</strong><br />
Szeregi potęgowe<br />
Szeregi Fouriera<br />
Ale:<br />
szereg nie musi być zbieżny w całej dziedzinie tej funkcji;<br />
nawet jeśli jest zbieżny, to jego suma nie musi być równa tej<br />
funkcji.<br />
Szeregi
Szeregi <strong>liczbowe</strong><br />
Szeregi potęgowe<br />
Szeregi Fouriera<br />
Ale:<br />
szereg nie musi być zbieżny w całej dziedzinie tej funkcji;<br />
nawet jeśli jest zbieżny, to jego suma nie musi być równa tej<br />
funkcji.<br />
Potrzebne są dodatkowe założenia.<br />
Szeregi
Szeregi <strong>liczbowe</strong><br />
Szeregi potęgowe<br />
Szeregi Fouriera<br />
Twierdzenie (o rozwijaniu funkcji w szereg Taylora)<br />
Jeżeli<br />
1 funkcja f ma na otoczeniu U punktu x 0 pochodne dowolnego<br />
rzędu;<br />
Szeregi
Szeregi <strong>liczbowe</strong><br />
Szeregi potęgowe<br />
Szeregi Fouriera<br />
Twierdzenie (o rozwijaniu funkcji w szereg Taylora)<br />
Jeżeli<br />
1 funkcja f ma na otoczeniu U punktu x 0 pochodne dowolnego<br />
rzędu;<br />
2 dla każdego x ∈ U reszta wzoru Taylora dąży do 0, tj.<br />
lim R n(x) = lim<br />
n→∞ n→∞<br />
f (n) (c)<br />
(x − x 0 ) n = 0,<br />
n!<br />
Szeregi
Szeregi <strong>liczbowe</strong><br />
Szeregi potęgowe<br />
Szeregi Fouriera<br />
Twierdzenie (o rozwijaniu funkcji w szereg Taylora)<br />
Jeżeli<br />
to<br />
1 funkcja f ma na otoczeniu U punktu x 0 pochodne dowolnego<br />
rzędu;<br />
2 dla każdego x ∈ U reszta wzoru Taylora dąży do 0, tj.<br />
dla każdego x ∈ U.<br />
lim R n(x) = lim<br />
n→∞ n→∞<br />
f (x) =<br />
∞∑<br />
n=0<br />
f (n) (c)<br />
(x − x 0 ) n = 0,<br />
n!<br />
f (n) (x 0 )<br />
(x − x 0 ) n<br />
n!<br />
Szeregi
Szeregi <strong>liczbowe</strong><br />
Szeregi potęgowe<br />
Szeregi Fouriera<br />
Przykłady. Posługując się powyższym wzorem wykazać, że dla<br />
x ∈ R<br />
∞∑<br />
e x 1<br />
=<br />
n! x n = 1 + x 1! + x 2<br />
2! + · · · ;<br />
n=0<br />
Szeregi
Szeregi <strong>liczbowe</strong><br />
Szeregi potęgowe<br />
Szeregi Fouriera<br />
Przykłady. Posługując się powyższym wzorem wykazać, że dla<br />
x ∈ R<br />
∞∑<br />
e x 1<br />
=<br />
n! x n = 1 + x 1! + x 2<br />
2! + · · · ;<br />
sin x =<br />
∞∑<br />
n=0<br />
n=0<br />
(−1) n<br />
(2n + 1)! x 2n+1 = x − x 3<br />
3! + x 5<br />
5! − x 7<br />
7! + · · · ;<br />
Szeregi
Szeregi <strong>liczbowe</strong><br />
Szeregi potęgowe<br />
Szeregi Fouriera<br />
Przykłady. Posługując się powyższym wzorem wykazać, że dla<br />
x ∈ R<br />
∞∑<br />
e x 1<br />
=<br />
n! x n = 1 + x 1! + x 2<br />
2! + · · · ;<br />
sin x =<br />
∞∑<br />
cos x =<br />
n=0<br />
∞∑<br />
n=0<br />
(−1) n<br />
(2n + 1)! x 2n+1 = x − x 3<br />
3! + x 5<br />
5! − x 7<br />
n=0<br />
(−1) n<br />
(2n)! x 2n = 1 − x 2<br />
2! + x 4<br />
4! − x 6<br />
7! + · · · ;<br />
6! + · · · .<br />
Szeregi
Szeregi <strong>liczbowe</strong><br />
Szeregi potęgowe<br />
Szeregi Fouriera<br />
Posługując się już wyprowadzonymi rozwinięciami można znaleźć<br />
dalsze wykonując operacje na szeregach (dodawanie, mnożenie<br />
przez stałą, całkowanie, różniczkowanie ...)<br />
Szeregi
Szeregi <strong>liczbowe</strong><br />
Szeregi potęgowe<br />
Szeregi Fouriera<br />
Posługując się już wyprowadzonymi rozwinięciami można znaleźć<br />
dalsze wykonując operacje na szeregach (dodawanie, mnożenie<br />
przez stałą, całkowanie, różniczkowanie ...)<br />
Przykłady. Wykorzystując równości sinh x = 1 2 (ex − e −x ),<br />
cosh x = 1 2 (ex + e −x ) wykazać, że dla x ∈ R<br />
Szeregi
Szeregi <strong>liczbowe</strong><br />
Szeregi potęgowe<br />
Szeregi Fouriera<br />
Posługując się już wyprowadzonymi rozwinięciami można znaleźć<br />
dalsze wykonując operacje na szeregach (dodawanie, mnożenie<br />
przez stałą, całkowanie, różniczkowanie ...)<br />
Przykłady. Wykorzystując równości sinh x = 1 2 (ex − e −x ),<br />
cosh x = 1 2 (ex + e −x ) wykazać, że dla x ∈ R<br />
sinh x =<br />
∞∑<br />
n=0<br />
x 2n+1<br />
(2n + 1)! = x + x 3<br />
3! + x 5<br />
5! + x 7<br />
7! + · · · ;<br />
Szeregi
Szeregi <strong>liczbowe</strong><br />
Szeregi potęgowe<br />
Szeregi Fouriera<br />
Posługując się już wyprowadzonymi rozwinięciami można znaleźć<br />
dalsze wykonując operacje na szeregach (dodawanie, mnożenie<br />
przez stałą, całkowanie, różniczkowanie ...)<br />
Przykłady. Wykorzystując równości sinh x = 1 2 (ex − e −x ),<br />
cosh x = 1 2 (ex + e −x ) wykazać, że dla x ∈ R<br />
sinh x =<br />
∞∑<br />
n=0<br />
cosh x =<br />
x 2n+1<br />
(2n + 1)! = x + x 3<br />
3! + x 5<br />
5! + x 7<br />
∞∑<br />
n=0<br />
x 2n<br />
(2n)! = 1 + x 2<br />
2! + x 4<br />
4! + x 6<br />
7! + · · · ;<br />
6! + · · · .<br />
Szeregi
Szeregi <strong>liczbowe</strong><br />
Szeregi potęgowe<br />
Szeregi Fouriera<br />
Przykład. Znana jest równość<br />
(szereg geometryczny).<br />
1<br />
∞<br />
1 − x = ∑<br />
x n dla x ∈ (−1, 1)<br />
n=0<br />
Szeregi
Szeregi <strong>liczbowe</strong><br />
Szeregi potęgowe<br />
Szeregi Fouriera<br />
Przykład. Znana jest równość<br />
1<br />
∞<br />
1 − x = ∑<br />
x n dla x ∈ (−1, 1)<br />
n=0<br />
(szereg geometryczny).<br />
Zamieniając w niej x na −x otrzymamy<br />
1<br />
∞<br />
1 + x = ∑<br />
(−1) n x n dla x ∈ (−1, 1).<br />
n=0<br />
Szeregi
Szeregi <strong>liczbowe</strong><br />
Szeregi potęgowe<br />
Szeregi Fouriera<br />
Przykład. Znana jest równość<br />
1<br />
∞<br />
1 − x = ∑<br />
x n dla x ∈ (−1, 1)<br />
n=0<br />
(szereg geometryczny).<br />
Zamieniając w niej x na −x otrzymamy<br />
Całkujemy od 0 do x:<br />
1<br />
∞<br />
1 + x = ∑<br />
(−1) n x n dla x ∈ (−1, 1).<br />
n=0<br />
ln(1 + x) =<br />
∫ x<br />
0<br />
1<br />
1 + t dt = Szeregi
Szeregi <strong>liczbowe</strong><br />
Szeregi potęgowe<br />
Szeregi Fouriera<br />
Przykład. Znana jest równość<br />
1<br />
∞<br />
1 − x = ∑<br />
x n dla x ∈ (−1, 1)<br />
n=0<br />
(szereg geometryczny).<br />
Zamieniając w niej x na −x otrzymamy<br />
Całkujemy od 0 do x:<br />
ln(1 + x) =<br />
1<br />
∞<br />
1 + x = ∑<br />
(−1) n x n dla x ∈ (−1, 1).<br />
∫ x<br />
0<br />
n=0<br />
1<br />
∞<br />
1 + t dt = ∑<br />
n=0<br />
∫ x<br />
0<br />
(−1) n t n dt =<br />
Szeregi
Szeregi <strong>liczbowe</strong><br />
Szeregi potęgowe<br />
Szeregi Fouriera<br />
Przykład. Znana jest równość<br />
1<br />
∞<br />
1 − x = ∑<br />
x n dla x ∈ (−1, 1)<br />
n=0<br />
(szereg geometryczny).<br />
Zamieniając w niej x na −x otrzymamy<br />
Całkujemy od 0 do x:<br />
1<br />
∞<br />
1 + x = ∑<br />
(−1) n x n dla x ∈ (−1, 1).<br />
n=0<br />
ln(1 + x) =<br />
∫ x<br />
0<br />
1<br />
∞<br />
1 + t dt = ∑<br />
n=0<br />
∫ x<br />
0<br />
(−1) n t n dt =<br />
∞∑<br />
n=0<br />
(−1) n<br />
n + 1 x n+1<br />
dla x ∈ (−1, 1).<br />
Szeregi
Szeregi <strong>liczbowe</strong><br />
Szeregi potęgowe<br />
Szeregi Fouriera<br />
Szereg geometryczny jest szczególnym przypadkiem ogólniejszego<br />
szeregu dwumianowego:<br />
(<br />
∞∑ α<br />
(1 + x) α = x<br />
n)<br />
n dla α ∈ R, x ∈ (−1, 1)<br />
n=0<br />
Szeregi
Szeregi <strong>liczbowe</strong><br />
Szeregi potęgowe<br />
Szeregi Fouriera<br />
Szereg geometryczny jest szczególnym przypadkiem ogólniejszego<br />
szeregu dwumianowego:<br />
(<br />
∞∑ α<br />
(1 + x) α = x<br />
n)<br />
n dla α ∈ R, x ∈ (−1, 1)<br />
n=0<br />
gdzie symbol ( α<br />
n) określamy następująco:<br />
(<br />
α α(α − 1)(α − 2) . . . (α − n + 1)<br />
= .<br />
n)<br />
n!<br />
Szeregi
Szeregi <strong>liczbowe</strong><br />
Szeregi potęgowe<br />
Szeregi Fouriera<br />
Szereg geometryczny jest szczególnym przypadkiem ogólniejszego<br />
szeregu dwumianowego:<br />
(<br />
∞∑ α<br />
(1 + x) α = x<br />
n)<br />
n dla α ∈ R, x ∈ (−1, 1)<br />
n=0<br />
gdzie symbol ( α<br />
n) określamy następująco:<br />
(<br />
α α(α − 1)(α − 2) . . . (α − n + 1)<br />
= .<br />
n)<br />
n!<br />
Przykładowo dla α = 1 3 mamy:<br />
3√<br />
1 + x = 1 +<br />
1<br />
3 x − 2<br />
2!3 2 x 2 + 2 · 5<br />
3!3 3 − 2 · 5 · 8<br />
4!3 4 + · · ·<br />
Szeregi
Szeregi <strong>liczbowe</strong><br />
Szeregi potęgowe<br />
Szeregi Fouriera<br />
Zastosowania szeregów potęgowych<br />
Znając rozkład funkcji w szereg Maclaurina można z dowolną<br />
dokładnością obliczyć wartości tej funkcji.<br />
Przykład Obliczyć 10√ e = e 1 10 z dokładnością 0, 00001.<br />
Szeregi
Szeregi <strong>liczbowe</strong><br />
Szeregi potęgowe<br />
Szeregi Fouriera<br />
Zastosowania szeregów potęgowych<br />
Znając rozkład funkcji w szereg Maclaurina można z dowolną<br />
dokładnością obliczyć wartości tej funkcji.<br />
Przykład Obliczyć 10√ e = e 1 10 z dokładnością 0, 00001.<br />
e 1 ∑ ∞ 1 1 ) n<br />
10 = =<br />
n!(<br />
10<br />
n=0<br />
Szeregi
Szeregi <strong>liczbowe</strong><br />
Szeregi potęgowe<br />
Szeregi Fouriera<br />
Zastosowania szeregów potęgowych<br />
Znając rozkład funkcji w szereg Maclaurina można z dowolną<br />
dokładnością obliczyć wartości tej funkcji.<br />
Przykład Obliczyć 10√ e = e 1 10 z dokładnością 0, 00001.<br />
e 1 ∑ ∞ 1 1 ) n 0, 1 0, 01 0, 001 0, 0001<br />
10 = = = 1 + + + + + · · ·<br />
n!(<br />
10<br />
1! 2! 3! 4!<br />
n=0<br />
Szeregi
Szeregi <strong>liczbowe</strong><br />
Szeregi potęgowe<br />
Szeregi Fouriera<br />
Zastosowania szeregów potęgowych<br />
Znając rozkład funkcji w szereg Maclaurina można z dowolną<br />
dokładnością obliczyć wartości tej funkcji.<br />
Przykład Obliczyć 10√ e = e 1 10 z dokładnością 0, 00001.<br />
e 1 ∑ ∞ 1 1 ) n 0, 1 0, 01 0, 001 0, 0001<br />
10 = = = 1 + + + + + · · ·<br />
n!(<br />
10<br />
1! 2! 3! 4!<br />
n=0<br />
Jeżeli dodamy pierwszych k wyrazów tego szeregu, to reszta<br />
szeregu jest postaci<br />
10 −k<br />
k!<br />
e ϑ , 0 < ϑ < 0,1<br />
Szeregi
Szeregi <strong>liczbowe</strong><br />
Szeregi potęgowe<br />
Szeregi Fouriera<br />
Zastosowania szeregów potęgowych<br />
Znając rozkład funkcji w szereg Maclaurina można z dowolną<br />
dokładnością obliczyć wartości tej funkcji.<br />
Przykład Obliczyć 10√ e = e 1 10 z dokładnością 0, 00001.<br />
e 1 ∑ ∞ 1 1 ) n 0, 1 0, 01 0, 001 0, 0001<br />
10 = = = 1 + + + + + · · ·<br />
n!(<br />
10<br />
1! 2! 3! 4!<br />
n=0<br />
Jeżeli dodamy pierwszych k wyrazów tego szeregu, to reszta<br />
szeregu jest postaci<br />
10 −k<br />
k!<br />
e ϑ , 0 < ϑ < 0,1<br />
Żądaną dokładność uzyskamy, gdy reszta będzie mniejsza od<br />
0, 00001. Wystarczy k = 4.<br />
Szeregi
Szeregi <strong>liczbowe</strong><br />
Szeregi potęgowe<br />
Szeregi Fouriera<br />
Zastosowania szeregów potęgowych<br />
Przy obliczaniu wartości ważne jest, jakiego szeregu użyjemy do<br />
obliczeń.<br />
Szeregi
Szeregi <strong>liczbowe</strong><br />
Szeregi potęgowe<br />
Szeregi Fouriera<br />
Zastosowania szeregów potęgowych<br />
Przy obliczaniu wartości ważne jest, jakiego szeregu użyjemy do<br />
obliczeń.<br />
Przykład Obliczyć ln 2.<br />
Szeregi
Szeregi <strong>liczbowe</strong><br />
Szeregi potęgowe<br />
Szeregi Fouriera<br />
Zastosowania szeregów potęgowych<br />
Przy obliczaniu wartości ważne jest, jakiego szeregu użyjemy do<br />
obliczeń.<br />
Przykład Obliczyć ln 2.<br />
Punktem wyjścia jest szereg<br />
ln(1 + x) =<br />
∞∑ (−1) n<br />
n + 1 x n+1 = x − x 2<br />
2 + x 3<br />
3 − · · · + (−1)n−1 x n + · · ·<br />
n<br />
n=0<br />
dla x ∈ (−1, 1].<br />
Szeregi
Szeregi <strong>liczbowe</strong><br />
Szeregi potęgowe<br />
Szeregi Fouriera<br />
Zastosowania szeregów potęgowych<br />
Przy obliczaniu wartości ważne jest, jakiego szeregu użyjemy do<br />
obliczeń.<br />
Przykład Obliczyć ln 2.<br />
Punktem wyjścia jest szereg<br />
ln(1 + x) =<br />
∞∑ (−1) n<br />
n + 1 x n+1 = x − x 2<br />
2 + x 3<br />
3 − · · · + (−1)n−1 x n + · · ·<br />
n<br />
n=0<br />
dla x ∈ (−1, 1].Podstawiając w nim x = 1 otrzymamy<br />
ln 2 = 1 − 1 2 + 1 3 − 1 4 + · · · + (−1)n−1 1 n + · · · .<br />
Szeregi
Szeregi <strong>liczbowe</strong><br />
Szeregi potęgowe<br />
Szeregi Fouriera<br />
Zastosowania szeregów potęgowych<br />
Przy obliczaniu wartości ważne jest, jakiego szeregu użyjemy do<br />
obliczeń.<br />
Przykład Obliczyć ln 2.<br />
Punktem wyjścia jest szereg<br />
ln(1 + x) =<br />
∞∑ (−1) n<br />
n + 1 x n+1 = x − x 2<br />
2 + x 3<br />
3 − · · · + (−1)n−1 x n + · · ·<br />
n<br />
n=0<br />
dla x ∈ (−1, 1].Podstawiając w nim x = 1 otrzymamy<br />
ln 2 = 1 − 1 2 + 1 3 − 1 4 + · · · + (−1)n−1 1 n + · · · .<br />
Szereg ten jest bardzo wolno zbieżny. Np. biorąc 10 wyrazów<br />
popełniamy błąd szacowany liczbą 1<br />
11 .<br />
Szeregi
Szeregi <strong>liczbowe</strong><br />
Szeregi potęgowe<br />
Szeregi Fouriera<br />
Zastosowania szeregów potęgowych<br />
Znajdziemy szereg znacznie szybciej zbieżny.<br />
Szeregi
Szeregi <strong>liczbowe</strong><br />
Szeregi potęgowe<br />
Szeregi Fouriera<br />
Zastosowania szeregów potęgowych<br />
Znajdziemy szereg znacznie szybciej zbieżny.<br />
W tym celu wykorzystamy szereg<br />
∞∑ x n+1<br />
ln(1 − x) = −<br />
n + 1 = −x − x 2<br />
2 − x 3<br />
3 − · · · − (−1)n−1 x n + · · ·<br />
n<br />
dla x ∈ [−1, 1).<br />
n=0<br />
Szeregi
Szeregi <strong>liczbowe</strong><br />
Szeregi potęgowe<br />
Szeregi Fouriera<br />
Zastosowania szeregów potęgowych<br />
Znajdziemy szereg znacznie szybciej zbieżny.<br />
W tym celu wykorzystamy szereg<br />
∞∑ x n+1<br />
ln(1 − x) = −<br />
n + 1 = −x − x 2<br />
2 − x 3<br />
3 − · · · − (−1)n−1 x n + · · ·<br />
n<br />
n=0<br />
dla x ∈ [−1, 1).Odejmując <strong>szeregi</strong> dla ln(1 + x) i ln(1 − x)<br />
otrzymamy<br />
ln 1 + x (<br />
1 − x = 2 x + x 3<br />
3 + x 5<br />
5 + x 7 )<br />
7 + · · · .<br />
Szeregi
Szeregi <strong>liczbowe</strong><br />
Szeregi potęgowe<br />
Szeregi Fouriera<br />
Zastosowania szeregów potęgowych<br />
Znajdziemy szereg znacznie szybciej zbieżny.<br />
W tym celu wykorzystamy szereg<br />
∞∑ x n+1<br />
ln(1 − x) = −<br />
n + 1 = −x − x 2<br />
2 − x 3<br />
3 − · · · − (−1)n−1 x n + · · ·<br />
n<br />
n=0<br />
dla x ∈ [−1, 1).Odejmując <strong>szeregi</strong> dla ln(1 + x) i ln(1 − x)<br />
otrzymamy<br />
ln 1 + x (<br />
1 − x = 2 x + x 3<br />
3 + x 5<br />
5 + x 7 )<br />
7 + · · · .<br />
Ponieważ 1+x<br />
1−x = 2 dla x = 1 3<br />
, więc podstawiając do powyższej<br />
równości x = 1 3 uzyskamy<br />
( 1<br />
ln 2 = 2<br />
3 + 1<br />
3 · 3 3 + 1<br />
5 · 3 5 + 1 )<br />
7 · 3 7 + · · · .<br />
Szeregi
Szeregi <strong>liczbowe</strong><br />
Szeregi potęgowe<br />
Szeregi Fouriera<br />
Zastosowania szeregów potęgowych<br />
Znajdziemy szereg znacznie szybciej zbieżny.<br />
W tym celu wykorzystamy szereg<br />
∞∑ x n+1<br />
ln(1 − x) = −<br />
n + 1 = −x − x 2<br />
2 − x 3<br />
3 − · · · − (−1)n−1 x n + · · ·<br />
n<br />
n=0<br />
dla x ∈ [−1, 1).Odejmując <strong>szeregi</strong> dla ln(1 + x) i ln(1 − x)<br />
otrzymamy<br />
ln 1 + x (<br />
1 − x = 2 x + x 3<br />
3 + x 5<br />
5 + x 7 )<br />
7 + · · · .<br />
Ponieważ 1+x<br />
1−x = 2 dla x = 1 3<br />
, więc podstawiając do powyższej<br />
równości x = 1 3 uzyskamy<br />
( 1<br />
ln 2 = 2<br />
3 + 1<br />
3 · 3 3 + 1<br />
5 · 3 5 + 1 )<br />
7 · 3 7 + · · · .<br />
Teraz biorąc 10 wyrazów popełniamy błąd niewiększy niż 10 −9 .<br />
Szeregi
Szeregi Fouriera<br />
Szeregi <strong>liczbowe</strong><br />
Szeregi potęgowe<br />
Szeregi Fouriera<br />
Szereg postaci<br />
1<br />
2 a 0 + (a 1 cos x + b 1 sin x) + (a 2 cos 2x + b 2 sin 2x) + · · · =<br />
= 1 ∞∑<br />
2 a 0 + a n cos nx + b n sin nx (6)<br />
n=1<br />
nazywamy <strong>szeregi</strong>em trygonometrycznym.<br />
Szeregi
Szeregi Fouriera<br />
Szeregi <strong>liczbowe</strong><br />
Szeregi potęgowe<br />
Szeregi Fouriera<br />
Szereg postaci<br />
1<br />
2 a 0 + (a 1 cos x + b 1 sin x) + (a 2 cos 2x + b 2 sin 2x) + · · · =<br />
= 1 ∞∑<br />
2 a 0 + a n cos nx + b n sin nx (6)<br />
n=1<br />
nazywamy <strong>szeregi</strong>em trygonometrycznym.<br />
Każdy wyraz tego szeregu jest funkcją trygonometryczną o okresie<br />
2π.<br />
Szeregi
Szeregi Fouriera<br />
Szeregi <strong>liczbowe</strong><br />
Szeregi potęgowe<br />
Szeregi Fouriera<br />
Szereg postaci<br />
1<br />
2 a 0 + (a 1 cos x + b 1 sin x) + (a 2 cos 2x + b 2 sin 2x) + · · · =<br />
= 1 ∞∑<br />
2 a 0 + a n cos nx + b n sin nx (6)<br />
n=1<br />
nazywamy <strong>szeregi</strong>em trygonometrycznym.<br />
Każdy wyraz tego szeregu jest funkcją trygonometryczną o okresie<br />
2π.<br />
Jeżeli szereg jest zbieżny w przedziale [−π, π], to jest zbieżny dla<br />
wszystkich x i jego suma jest funkcją okresową.<br />
Szeregi
Szeregi Fouriera<br />
Szeregi <strong>liczbowe</strong><br />
Szeregi potęgowe<br />
Szeregi Fouriera<br />
Szereg postaci<br />
1<br />
2 a 0 + (a 1 cos x + b 1 sin x) + (a 2 cos 2x + b 2 sin 2x) + · · · =<br />
= 1 ∞∑<br />
2 a 0 + a n cos nx + b n sin nx (6)<br />
n=1<br />
nazywamy <strong>szeregi</strong>em trygonometrycznym.<br />
Każdy wyraz tego szeregu jest funkcją trygonometryczną o okresie<br />
2π.<br />
Jeżeli szereg jest zbieżny w przedziale [−π, π], to jest zbieżny dla<br />
wszystkich x i jego suma jest funkcją okresową.<br />
Stąd wynika, że rozwinięcie w szereg trygonometryczny mogą mieć<br />
tylko funkcje okresowe o okresie 2π.<br />
Szeregi
Szeregi <strong>liczbowe</strong><br />
Szeregi potęgowe<br />
Szeregi Fouriera<br />
Zadanie. Przypuśmy, że funkcja f (x), o okresie 2π, ma<br />
przedstawienie<br />
f (x) = 1 ∞∑<br />
2 a 0 + a n cos nx + b n sin nx. (7)<br />
n=1<br />
Szeregi
Szeregi <strong>liczbowe</strong><br />
Szeregi potęgowe<br />
Szeregi Fouriera<br />
Zadanie. Przypuśmy, że funkcja f (x), o okresie 2π, ma<br />
przedstawienie<br />
f (x) = 1 ∞∑<br />
2 a 0 + a n cos nx + b n sin nx. (7)<br />
n=1<br />
Ile wynoszą współczynniki a n i b n <br />
Szeregi
Szeregi <strong>liczbowe</strong><br />
Szeregi potęgowe<br />
Szeregi Fouriera<br />
Zadanie. Przypuśmy, że funkcja f (x), o okresie 2π, ma<br />
przedstawienie<br />
f (x) = 1 ∞∑<br />
2 a 0 + a n cos nx + b n sin nx. (7)<br />
n=1<br />
Ile wynoszą współczynniki a n i b n <br />
Zauważmy najpierw, że dla n ∈ N jest ∫ π<br />
sin x dx = 0.<br />
Szeregi<br />
∫ π<br />
−π<br />
−π<br />
cos x dx = 0 oraz
Szeregi <strong>liczbowe</strong><br />
Szeregi potęgowe<br />
Szeregi Fouriera<br />
Zadanie. Przypuśmy, że funkcja f (x), o okresie 2π, ma<br />
przedstawienie<br />
f (x) = 1 ∞∑<br />
2 a 0 + a n cos nx + b n sin nx. (7)<br />
n=1<br />
Ile wynoszą współczynniki a n i b n <br />
Zauważmy najpierw, że dla n ∈ N jest ∫ π<br />
∫ π<br />
−π<br />
sin x dx = 0.<br />
Zatem całkując równość (7) otrzymamy<br />
∫ π<br />
−π<br />
f (x) dx = 1 2 a 0<br />
∫ π<br />
−π<br />
−π<br />
cos x dx = 0 oraz<br />
dx = a 0 π,<br />
Szeregi
Szeregi <strong>liczbowe</strong><br />
Szeregi potęgowe<br />
Szeregi Fouriera<br />
Zadanie. Przypuśmy, że funkcja f (x), o okresie 2π, ma<br />
przedstawienie<br />
f (x) = 1 ∞∑<br />
2 a 0 + a n cos nx + b n sin nx. (7)<br />
n=1<br />
Ile wynoszą współczynniki a n i b n <br />
Zauważmy najpierw, że dla n ∈ N jest ∫ π<br />
∫ π<br />
−π<br />
sin x dx = 0.<br />
Zatem całkując równość (7) otrzymamy<br />
∫ π<br />
−π<br />
f (x) dx = 1 2 a 0<br />
∫ π<br />
−π<br />
−π<br />
cos x dx = 0 oraz<br />
dx = a 0 π,<br />
a więc<br />
a 0 = 1 π<br />
∫ π<br />
−π<br />
f (x) dx.<br />
Szeregi
Szeregi <strong>liczbowe</strong><br />
Szeregi potęgowe<br />
Szeregi Fouriera<br />
Aby obliczyć a n dla n > 0 mnożymy najpierw równość (7) zapisaną<br />
w postaci<br />
f (x) = 1 2 a 0 +<br />
∞∑<br />
a k cos kx + b k sin kx<br />
k=1<br />
przez cos nx i potem całkujemy:<br />
Szeregi
Szeregi <strong>liczbowe</strong><br />
Szeregi potęgowe<br />
Szeregi Fouriera<br />
Aby obliczyć a n dla n > 0 mnożymy najpierw równość (7) zapisaną<br />
w postaci<br />
f (x) = 1 2 a 0 +<br />
∞∑<br />
a k cos kx + b k sin kx<br />
k=1<br />
przez cos nx i potem całkujemy:<br />
+<br />
∫ π<br />
−π<br />
∞∑<br />
k=1<br />
f (x) cos nx dx = 1 2 a 0<br />
(a k<br />
∫ π<br />
−π<br />
∫ π<br />
−π<br />
cos nx dx +<br />
cos kx cos nx dx + b k<br />
∫ π<br />
−π<br />
)<br />
sin kx cos nx dx .<br />
Szeregi
Szeregi <strong>liczbowe</strong><br />
Szeregi potęgowe<br />
Szeregi Fouriera<br />
Ale całki ∫ π<br />
−π<br />
cos kx cos nx dx są równe 0 dla k ≠ n.<br />
Szeregi
Szeregi <strong>liczbowe</strong><br />
Szeregi potęgowe<br />
Szeregi Fouriera<br />
Ale całki ∫ π<br />
−π<br />
cos kx cos nx dx są równe 0 dla k ≠ n.<br />
Żeby to stwierdzić, wystarczy skorzystać ze wzoru<br />
trygonometrycznego<br />
cos kx cos nx = 1 (cos(k + n)x + cos(k − n)x).<br />
2<br />
Szeregi
Szeregi <strong>liczbowe</strong><br />
Szeregi potęgowe<br />
Szeregi Fouriera<br />
Ale całki ∫ π<br />
−π<br />
cos kx cos nx dx są równe 0 dla k ≠ n.<br />
Żeby to stwierdzić, wystarczy skorzystać ze wzoru<br />
trygonometrycznego<br />
cos kx cos nx = 1 (cos(k + n)x + cos(k − n)x).<br />
2<br />
Również ∫ π<br />
−π<br />
sin kx cos nx dx są równe 0 dla k ∈ N. Tym razem<br />
korzystamy ze wzoru trygonometrycznego<br />
sin kx cos nx = 1 (sin(k + n)x + sin(k − n)x).<br />
2<br />
Szeregi
Szeregi <strong>liczbowe</strong><br />
Szeregi potęgowe<br />
Szeregi Fouriera<br />
Ale całki ∫ π<br />
−π<br />
cos kx cos nx dx są równe 0 dla k ≠ n.<br />
Żeby to stwierdzić, wystarczy skorzystać ze wzoru<br />
trygonometrycznego<br />
cos kx cos nx = 1 (cos(k + n)x + cos(k − n)x).<br />
2<br />
Również ∫ π<br />
−π<br />
sin kx cos nx dx są równe 0 dla k ∈ N. Tym razem<br />
korzystamy ze wzoru trygonometrycznego<br />
sin kx cos nx = 1 (sin(k + n)x + sin(k − n)x).<br />
2<br />
A zatem jedyną niezerową całką po prawej stronie jest<br />
∫ π<br />
−π cos2 nx dx = π. Zatem mamy<br />
∫ π<br />
−π<br />
f (x) cos nx dx = a n<br />
∫ π<br />
−π<br />
cos 2 nx dx = πa n ,<br />
Szeregi
Szeregi <strong>liczbowe</strong><br />
Szeregi potęgowe<br />
Szeregi Fouriera<br />
skąd otrzymujemy<br />
a n = 1 π<br />
∫ π<br />
−π<br />
f (x) cos nx dx.<br />
Szeregi
Szeregi <strong>liczbowe</strong><br />
Szeregi potęgowe<br />
Szeregi Fouriera<br />
skąd otrzymujemy<br />
a n = 1 π<br />
∫ π<br />
−π<br />
f (x) cos nx dx.<br />
Analogicznie znajdziemy wzór na b n ; należy pomnożyć równość (7)<br />
przez sin nx i całkować, korzystając przy tym ze wzoru<br />
∫ π<br />
−π<br />
sin kx sin nx dx = 0 dla k ≠ n. Tę zależność otrzymamy<br />
wykorzystując równość<br />
sin kx sin nx = 1 (cos(k − n)x − cos(k + n)x).<br />
2<br />
Szeregi
Szeregi <strong>liczbowe</strong><br />
Szeregi potęgowe<br />
Szeregi Fouriera<br />
skąd otrzymujemy<br />
a n = 1 π<br />
∫ π<br />
−π<br />
f (x) cos nx dx.<br />
Analogicznie znajdziemy wzór na b n ; należy pomnożyć równość (7)<br />
przez sin nx i całkować, korzystając przy tym ze wzoru<br />
∫ π<br />
−π<br />
sin kx sin nx dx = 0 dla k ≠ n. Tę zależność otrzymamy<br />
wykorzystując równość<br />
sin kx sin nx = 1 (cos(k − n)x − cos(k + n)x).<br />
2<br />
Po rachunkach podobnych do poprzednich uzyskamy:<br />
b n = 1 π<br />
∫ π<br />
−π<br />
f (x) sin nx dx.<br />
Szeregi
Szeregi <strong>liczbowe</strong><br />
Szeregi potęgowe<br />
Szeregi Fouriera<br />
Otrzymane wzory<br />
a 0 = 1 π<br />
∫ π<br />
−π<br />
f (x) dx,<br />
Szeregi
Szeregi <strong>liczbowe</strong><br />
Szeregi potęgowe<br />
Szeregi Fouriera<br />
Otrzymane wzory<br />
a 0 = 1 π<br />
a n = 1 π<br />
∫ π<br />
−π<br />
∫ π<br />
−π<br />
f (x) dx,<br />
f (x) cos nx dx.<br />
Szeregi
Szeregi <strong>liczbowe</strong><br />
Szeregi potęgowe<br />
Szeregi Fouriera<br />
Otrzymane wzory<br />
a 0 = 1 π<br />
a n = 1 π<br />
b n = 1 π<br />
∫ π<br />
−π<br />
∫ π<br />
−π<br />
∫ π<br />
−π<br />
nazywamy wzorami Eulera-Fouriera.<br />
f (x) dx,<br />
f (x) cos nx dx.<br />
f (x) sin nx dx.<br />
Szeregi
Szeregi <strong>liczbowe</strong><br />
Szeregi potęgowe<br />
Szeregi Fouriera<br />
Stosując te wzory można dla dowolnej funkcji całkowalnej w<br />
przedziale [−π, π] utworzyć szereg trygonometryczny nazywany<br />
<strong>szeregi</strong>em Fouriera funkcji f (x).<br />
Szeregi
Szeregi <strong>liczbowe</strong><br />
Szeregi potęgowe<br />
Szeregi Fouriera<br />
Stosując te wzory można dla dowolnej funkcji całkowalnej w<br />
przedziale [−π, π] utworzyć szereg trygonometryczny nazywany<br />
<strong>szeregi</strong>em Fouriera funkcji f (x).<br />
Ale ten szereg nie musi być wcale zbieżny.<br />
Szeregi
Szeregi <strong>liczbowe</strong><br />
Szeregi potęgowe<br />
Szeregi Fouriera<br />
Stosując te wzory można dla dowolnej funkcji całkowalnej w<br />
przedziale [−π, π] utworzyć szereg trygonometryczny nazywany<br />
<strong>szeregi</strong>em Fouriera funkcji f (x).<br />
Ale ten szereg nie musi być wcale zbieżny.<br />
A jeśli nawet jest zbieżny, to niekoniecznie do funkcji f (x). Żeby to<br />
zapewnić potrzebne są dodatkowe założenia.<br />
Definicja<br />
Mówimy, że funkcja f (x) spełnia warunki Dirichleta, gdy<br />
1 f (x) jest przedziałami monotoniczna w [−π, π];<br />
Szeregi
Szeregi <strong>liczbowe</strong><br />
Szeregi potęgowe<br />
Szeregi Fouriera<br />
Stosując te wzory można dla dowolnej funkcji całkowalnej w<br />
przedziale [−π, π] utworzyć szereg trygonometryczny nazywany<br />
<strong>szeregi</strong>em Fouriera funkcji f (x).<br />
Ale ten szereg nie musi być wcale zbieżny.<br />
A jeśli nawet jest zbieżny, to niekoniecznie do funkcji f (x). Żeby to<br />
zapewnić potrzebne są dodatkowe założenia.<br />
Definicja<br />
Mówimy, że funkcja f (x) spełnia warunki Dirichleta, gdy<br />
1 f (x) jest przedziałami monotoniczna w [−π, π];<br />
2 f (x) = 1 2<br />
(f (x − 0) + f (x + 0)) dla x ∈ (−π, π);<br />
Szeregi
Szeregi <strong>liczbowe</strong><br />
Szeregi potęgowe<br />
Szeregi Fouriera<br />
Stosując te wzory można dla dowolnej funkcji całkowalnej w<br />
przedziale [−π, π] utworzyć szereg trygonometryczny nazywany<br />
<strong>szeregi</strong>em Fouriera funkcji f (x).<br />
Ale ten szereg nie musi być wcale zbieżny.<br />
A jeśli nawet jest zbieżny, to niekoniecznie do funkcji f (x). Żeby to<br />
zapewnić potrzebne są dodatkowe założenia.<br />
Definicja<br />
Mówimy, że funkcja f (x) spełnia warunki Dirichleta, gdy<br />
1 f (x) jest przedziałami monotoniczna w [−π, π];<br />
2 f (x) = 1 2<br />
(f (x − 0) + f (x + 0)) dla x ∈ (−π, π);<br />
3 f (−π) = f (π) = 1 2<br />
(f (−π + 0) + f (π − 0)).<br />
Szeregi
Szeregi <strong>liczbowe</strong><br />
Szeregi potęgowe<br />
Szeregi Fouriera<br />
Stosując te wzory można dla dowolnej funkcji całkowalnej w<br />
przedziale [−π, π] utworzyć szereg trygonometryczny nazywany<br />
<strong>szeregi</strong>em Fouriera funkcji f (x).<br />
Ale ten szereg nie musi być wcale zbieżny.<br />
A jeśli nawet jest zbieżny, to niekoniecznie do funkcji f (x). Żeby to<br />
zapewnić potrzebne są dodatkowe założenia.<br />
Definicja<br />
Mówimy, że funkcja f (x) spełnia warunki Dirichleta, gdy<br />
1 f (x) jest przedziałami monotoniczna w [−π, π];<br />
2 f (x) = 1 2<br />
(f (x − 0) + f (x + 0)) dla x ∈ (−π, π);<br />
3 f (−π) = f (π) = 1 2<br />
(f (−π + 0) + f (π − 0)).<br />
Symbole f (x − 0) i f (x + 0) oznaczają granicę lewostronną i<br />
prawostronną w punkcie x.<br />
Szeregi
Szeregi <strong>liczbowe</strong><br />
Szeregi potęgowe<br />
Szeregi Fouriera<br />
Twierdzenie (Dirichleta)<br />
Jeżeli funkcja f (x) spełnia warunki Dirichleta, to jej szereg<br />
Fouriera jest zbieżny do funkcji f (x) w przedziale [−π, π].<br />
Szeregi
Szeregi <strong>liczbowe</strong><br />
Szeregi potęgowe<br />
Szeregi Fouriera<br />
Twierdzenie (Dirichleta)<br />
Jeżeli funkcja f (x) spełnia warunki Dirichleta, to jej szereg<br />
Fouriera jest zbieżny do funkcji f (x) w przedziale [−π, π].<br />
Poza tym przedziałem równość zachodzi jedynie wtedy, gdy funkcja<br />
f (x) jest okresowa o okresie 2π.<br />
Szeregi
Szeregi <strong>liczbowe</strong><br />
Szeregi potęgowe<br />
Szeregi Fouriera<br />
Przykład Znajdziemy szereg Fouriera funkcji f (x) = |x|.<br />
Obliczamy<br />
a 0 = π, a n = 2<br />
πn 2 [(−1)n − 1], b n = 0.<br />
Szeregi
Szeregi <strong>liczbowe</strong><br />
Szeregi potęgowe<br />
Szeregi Fouriera<br />
Przykład Znajdziemy szereg Fouriera funkcji f (x) = |x|.<br />
Obliczamy<br />
Zatem<br />
a 0 = π, a n = 2<br />
πn 2 [(−1)n − 1], b n = 0.<br />
∞∑<br />
|x| = 1 2 π + 2 π<br />
= π 2 − 4 ∞∑<br />
π<br />
n=1<br />
k=1<br />
1<br />
n 2 [(−1)n − 1] cos nx =<br />
1<br />
cos(2k − 1)x<br />
(2k − 1) 2<br />
dla x ∈ [−π, π].<br />
Szeregi
Szeregi <strong>liczbowe</strong><br />
Szeregi potęgowe<br />
Szeregi Fouriera<br />
Przykład Dla funkcji f (x) = x cos x obliczamy<br />
a 0 = 0 a n = 0, b 1 = − 1 2 , b n = 2n<br />
n 2 − 1 (−1)n dla n > 1.<br />
Szeregi
Szeregi <strong>liczbowe</strong><br />
Szeregi potęgowe<br />
Szeregi Fouriera<br />
Przykład Dla funkcji f (x) = x cos x obliczamy<br />
a 0 = 0 a n = 0, b 1 = − 1 2 , b n = 2n<br />
n 2 − 1 (−1)n dla n > 1.<br />
A więc<br />
dla x ∈ (−π, π).<br />
x cos x = − 1 2 sin x + ∞ ∑<br />
n=2<br />
2n<br />
n 2 − 1 (−1)n sin nx<br />
Szeregi
Szeregi <strong>liczbowe</strong><br />
Szeregi potęgowe<br />
Szeregi Fouriera<br />
Przykład Dla funkcji f (x) = x cos x obliczamy<br />
a 0 = 0 a n = 0, b 1 = − 1 2 , b n = 2n<br />
n 2 − 1 (−1)n dla n > 1.<br />
A więc<br />
x cos x = − 1 2 sin x + ∞ ∑<br />
n=2<br />
2n<br />
n 2 − 1 (−1)n sin nx<br />
dla x ∈ (−π, π).<br />
Równość zachodzi tylko w przedziale otwartym, bo trzeci warunek<br />
Dirichleta nie jest spełniony.<br />
Szeregi
Szeregi <strong>liczbowe</strong><br />
Szeregi potęgowe<br />
Szeregi Fouriera<br />
Przykład Niech<br />
f (x) =<br />
Szereg Fouriera tej funkcji:<br />
f (x) = π ∞ 4 − ∑<br />
[ 2<br />
π<br />
n=1<br />
{<br />
0 dla −π < x < 0<br />
x dla 0 x < π<br />
· cos(2n − 1)x<br />
(2n − 1) 2 + (−1)<br />
n sin nx<br />
n<br />
]<br />
.<br />
Szeregi