- Page 1 and 2:
Foundations of Data Science ∗ Avr
- Page 3 and 4:
4.4 Branching Processes . . . . . .
- Page 5 and 6:
8.2.2 Structural properties of the
- Page 7 and 8:
12.4.7 Median . . . . . . . . . . .
- Page 9 and 10:
densities, discrete optimization, e
- Page 11 and 12:
2 High-Dimensional Space 2.1 Introd
- Page 13 and 14:
Also, if x and y are independent, t
- Page 15 and 16:
1 1 − ɛ Annulus of width 1 d Fig
- Page 17 and 18:
integral gives ∫ ∞ 0 e −r2 r
- Page 19 and 20:
The volume of the hemisphere below
- Page 21 and 22:
points onto the circle. In higher d
- Page 23 and 24:
Using the substitution 2z = y 2 , |
- Page 25 and 26:
For the nearest neighbor problem, i
- Page 27 and 28:
√ √ 2d+O(1) ≤ 2d + ∆2 −O(
- Page 29 and 30: 2.10 Bibliographic Notes The word v
- Page 31 and 32: Exercise 2.9 A 3-dimensional cube h
- Page 33 and 34: Exercise 2.26 Explain how the volum
- Page 35 and 36: Exercise 2.40 Consider a non orthog
- Page 37 and 38: 1 Exercise 2.50 Use the probability
- Page 39 and 40: This decomposition of A can be view
- Page 41 and 42: 3.3 Singular Vectors We now define
- Page 43 and 44: orthonormal basis w 1 , w 2 , . . .
- Page 45 and 46: A n × d = U n × r D r × r V T r
- Page 47 and 48: 3.6 Left Singular Vectors Theorem 3
- Page 49 and 50: Lemma 3.10 (Analog of eigenvalues a
- Page 51 and 52: Proof: Let A = r∑ σ i u i vi T i
- Page 53 and 54: a i , let dist(a i , l) denote its
- Page 55 and 56: such models. Mixture models are a v
- Page 57 and 58: 1. The best fit 1-dimension subspac
- Page 59 and 60: This leads to the following theorem
- Page 61 and 62: Thus, the maximum cut problem can b
- Page 63 and 64: and this meets the claimed error bo
- Page 65 and 66: (0,3) (1,1) (3,0) ⎛ M = ⎝ 1 1 0
- Page 67 and 68: Exercise 3.18 Modify the power meth
- Page 69 and 70: 2. What percent of the Forbenius no
- Page 71 and 72: City Bei- Tian- Shang- Chong- Hoh-
- Page 73 and 74: 5 10 15 20 25 30 35 40 4 9 14 19 24
- Page 75 and 76: Prob(vertex has degree k) = ( ) n
- Page 77 and 78: and thus k k ≤ n. Since k! ≤ k
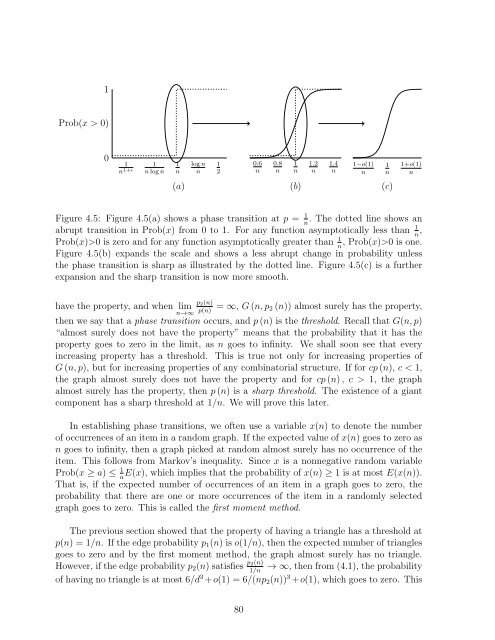
- Page 79: For x to be equal to zero, it must
- Page 83 and 84: Our first task is to figure out wha
- Page 85 and 86: √ Thus, the probability for all s
- Page 87 and 88: Figure 4.7: A degree three vertex w
- Page 89 and 90: ftp://ftp.cs.rochester.edu/pub/u/jo
- Page 91 and 92: Size of frontier 0 ln n nθ n Numbe
- Page 93 and 94: For a small number i of steps, the
- Page 95 and 96: same or are disjoint, ⎛( n∑ )
- Page 97 and 98: are O(ln n) in size and the expecte
- Page 99 and 100: f(x) q p 0 f(f(x)) f(x) x Figure 4.
- Page 101 and 102: may be infinite. That is, ∞∑ i=
- Page 103 and 104: Property cycles 1/n giant component
- Page 105 and 106: Keep in mind that the leading terms
- Page 107 and 108: 4.6 Phase Transitions for Increasin
- Page 109 and 110: p(n) A symmetric argument shows tha
- Page 111 and 112: simple. We supply some intuition be
- Page 113 and 114: Proof: Say that t is a “busy time
- Page 115 and 116: Consider a graph in which half of t
- Page 117 and 118: problem contributes a minuscule err
- Page 119 and 120: one. On the other hand, for δ = 1,
- Page 121 and 122: for all δ greater than δ critical
- Page 123 and 124: expected degree d i = 1, 2, 3 √ t
- Page 125 and 126: Destination Figure 4.17: For d < 2,
- Page 127 and 128: For at least half of the pairs of v
- Page 129 and 130: S i+1 is (1 − 1 ) |Si| ≤ 1 −
- Page 131 and 132:
Exercise 4.7 Let f (n) be a functio
- Page 133 and 134:
Exercise 4.19 (Birthday problem) Wh
- Page 135 and 136:
Exercise 4.38 Consider a model of a
- Page 137 and 138:
Exercise 4.53 Consider graph 3-colo
- Page 139 and 140:
5 Random Walks and Markov Chains A
- Page 141 and 142:
A B C (a) A B C (b) Figure 5.1: (a)
- Page 143 and 144:
in time polynomial in n. A quantity
- Page 145 and 146:
5.2 Markov Chain Monte Carlo The Ma
- Page 147 and 148:
p(a) = 1 2 p(b) = 1 4 p(c) = 1 8 p(
- Page 149 and 150:
5 8 7 12 1 3 1 6 1 8 1 3 3,1 3,2 3,
- Page 151 and 152:
Figure 5.4: A network with a constr
- Page 153 and 154:
There is a simple interpretation of
- Page 155 and 156:
Let γ i = π 1 + π 2 + · · · +
- Page 157 and 158:
5.4.1 Using Normalized Conductance
- Page 159 and 160:
The Gaussian distribution on the in
- Page 161 and 162:
6 6 1 8 1 5 8 4 5 5 Graph with boun
- Page 163 and 164:
and then reaching a from y before r
- Page 165 and 166:
every vertex? Hitting time The hitt
- Page 167 and 168:
clique of size n/2 x y } {{ } n/2 F
- Page 169 and 170:
i ↑ ↓ ↑ ↓ ↑ j ↑ =⇒ i
- Page 171 and 172:
Theorem 5.13 Let G be an undirected
- Page 173 and 174:
0 1 2 3 4 12 20 Number of resistors
- Page 175 and 176:
1 2 4 Figure 5.11: Paths obtained f
- Page 177 and 178:
whereas, with k self-loops, the equ
- Page 179 and 180:
or p[I − (1 − α)A] = α (1, 1,
- Page 181 and 182:
Exercise 5.10 Let p be a probabilit
- Page 183 and 184:
i 1 i 2 R 1 R 2 R 3 Figure 5.13: An
- Page 185 and 186:
(a) 1 2 3 4 (b) 1 2 3 4 (c) 1 2 3 4
- Page 187 and 188:
Exercise 5.40 Suppose that the cliq
- Page 189 and 190:
Exercise 5.55 Using a web browser b
- Page 191 and 192:
will allow us to make mathematical
- Page 193 and 194:
Not spam { }} { { Spam }} { x 1 x 2
- Page 195 and 196:
1 ∨ x 8 = 1}, or more succinctly,
- Page 197 and 198:
described using O(k log d) bits: lo
- Page 199 and 200:
In fact, we can show this bound is
- Page 201 and 202:
y definition of w ∗ . Similarly,
- Page 203 and 204:
y x φ Figure 6.4: Data that is not
- Page 205 and 206:
Theorem 6.11 (Online to Batch via R
- Page 207 and 208:
function of concept class H, will g
- Page 209 and 210:
Corollary 6.16 (VC-dimension sample
- Page 211 and 212:
A sphere in d-dimensions is a set o
- Page 213 and 214:
then with probability ≥ 1 − δ,
- Page 215 and 216:
work on a variety of measures. One
- Page 217 and 218:
Since weight(0) = n, the total weig
- Page 219 and 220:
Stochastic Gradient Descent: Given:
- Page 221 and 222:
sleeping experts problem. Combining
- Page 223 and 224:
⎫ ⎪⎬ ⎪⎭ Each gate is conn
- Page 225 and 226:
W 1 W 2 W 1 W 2 W 3 (a) (b) Figure
- Page 227 and 228:
convolution pooling Image Convoluti
- Page 229 and 230:
discard separators in advance that
- Page 231 and 232:
6.14.2 Active learning Active learn
- Page 233 and 234:
6.16 Exercises Exercise 6.1 (Sectio
- Page 235 and 236:
√ L log(L(T )) |S|) will be at mo
- Page 237 and 238:
7 Algorithms for Massive Data Probl
- Page 239 and 240:
important to know if some popular s
- Page 241 and 242:
We now give an example of a 2-unive
- Page 243 and 244:
estimate of m. To obtain a coin tha
- Page 245 and 246:
expected value of the sum will be z
- Page 247 and 248:
δ have values in ±1. There are ex
- Page 249 and 250:
mean. (ii) There is “no free lunc
- Page 251 and 252:
⎡ ⎢ ⎣ A m × n ⎤ ⎡ ⎥
- Page 253 and 254:
One uses the primitive in Section ?
- Page 255 and 256:
would require s ≥ n, which clearl
- Page 257 and 258:
its that capture sufficient informa
- Page 259 and 260:
7.6 Exercises Algorithms for Massiv
- Page 261 and 262:
Counting Frequent Elements The Majo
- Page 263 and 264:
Exercise 7.30 Blast: Given a long s
- Page 265 and 266:
Preliminaries: We will follow the s
- Page 267 and 268:
B A Figure 8.1: Example where the n
- Page 269 and 270:
Lloyd’s algorithm: Start with k c
- Page 271 and 272:
8.2.5 k-means clustering on the lin
- Page 273 and 274:
a clustering that is ɛ-close to C
- Page 275 and 276:
Theorem 8.5 Assume A satisfies (c,
- Page 277 and 278:
probability is q (where, q < p). 32
- Page 279 and 280:
8.6.4 Spectral Clustering Algorithm
- Page 281 and 282:
But for l ≠ l ′ , by hypothesis
- Page 283 and 284:
4. the σ-interior of the clusters
- Page 285 and 286:
Figure 8.4: Example of a bipartite
- Page 287 and 288:
are likely to be balanced given tha
- Page 289 and 290:
s 1 ∞ ∞ λ t ∞ edges and vert
- Page 291 and 292:
A clustering algorithm is consisten
- Page 293 and 294:
less than n, then richness is not r
- Page 295 and 296:
8.13 Exercises Exercise 8.1 Constru
- Page 297 and 298:
A B Figure 8.8: insert caption Exer
- Page 299 and 300:
9 Topic Models, Hidden Markov Proce
- Page 301 and 302:
Nonnegative matrix factorization (N
- Page 303 and 304:
This is a linear program. As we rem
- Page 305 and 306:
for t = 1 to T Prob(O 0 O 1 · ·
- Page 307 and 308:
a ij transition probability from st
- Page 309 and 310:
C 1 S 2 C 2 causes D 1 D 2 diseases
- Page 311 and 312:
x 1 + x 2 + x 3 x 1 + x 2 x 1 + x 3
- Page 313 and 314:
x 1 x 1 + x 2 + x 3 x 3 + x 4 + x 5
- Page 315 and 316:
the messages coming to a variable n
- Page 317 and 318:
y 2 y 3 x 2 x 3 y 1 x 1 x 4 y 4 y n
- Page 319 and 320:
two pieces of information, the valu
- Page 321 and 322:
graph. The vertices of Π are denot
- Page 323 and 324:
present and ask how correlated this
- Page 325 and 326:
Now consider a very tall tree. If t
- Page 327 and 328:
9.14 Exercises Exercise 9.1 Find a
- Page 329 and 330:
10 Other Topics 10.1 Rankings Ranki
- Page 331 and 332:
b . a . a b b b b . . b b a a b b .
- Page 333 and 334:
In the discrete case, x = [x 0 , x
- Page 335 and 336:
Figure 10.3: Some subgradients for
- Page 337 and 338:
Suppose ˜x 0 were another minimum.
- Page 339 and 340:
A T S A S is invertible. We will pr
- Page 341 and 342:
was included, we would just multipl
- Page 343 and 344:
position on genome trees = Phenotyp
- Page 345 and 346:
form a matrix, called the Hessian,
- Page 347 and 348:
The simplex algorithm is a classica
- Page 349 and 350:
This problem is NP-hard. One way to
- Page 351 and 352:
10.9 Exercises Exercise 10.1 Select
- Page 353 and 354:
Exercise 10.18 Repeat the above exe
- Page 355 and 356:
Lemma 11.1 If a dilation equation i
- Page 357 and 358:
The Haar Wavelet ⎧ ⎨ 1 0 ≤ x
- Page 359 and 360:
11.3 Wavelet Systems So far we have
- Page 361 and 362:
11.5 Conditions on the Dilation Equ
- Page 363 and 364:
the support of both sides of the eq
- Page 365 and 366:
and the wavelet functions are ortho
- Page 367 and 368:
11.7 Sufficient Conditions for the
- Page 369 and 370:
Example of orthogonality when wavel
- Page 371 and 372:
11.9 Designing a Wavelet System In
- Page 373 and 374:
3. f(x) = 1 2 f(2x) + 1 2 f(2x −
- Page 375 and 376:
12 Appendix 12.1 Asymptotic Notatio
- Page 377 and 378:
these equalities by derivatives.
- Page 379 and 380:
Gaussian and related integrals To v
- Page 381 and 382:
1 + x ≤ e x for all real x (1 −
- Page 383 and 384:
Thus, n! ≤ n n e −n√ ne. For
- Page 385 and 386:
from which the current inequality f
- Page 387 and 388:
Example: Let f (x) = x k for k an e
- Page 389 and 390:
Random variables x 1 , x 2 , . . .
- Page 391 and 392:
12.4.7 Median One often calculates
- Page 393 and 394:
The density of y is the unit varian
- Page 395 and 396:
Generation of random numbers accord
- Page 397 and 398:
Example: Consider flipping a coin 1
- Page 399 and 400:
Setting λ = ln(1 + δ) Prob ( s >
- Page 401 and 402:
12.5 Bounds on Tail Probability Aft
- Page 403 and 404:
Collect terms of the summation with
- Page 405 and 406:
The first integral is just the stan
- Page 407 and 408:
of a symmetric matrix, counting mul
- Page 409 and 410:
capture this situation. Now AA T =
- Page 411 and 412:
The above theorem tells us that the
- Page 413 and 414:
Important special cases are |x| 0 t
- Page 415 and 416:
Lemma 12.23 Let A be a symmetric ma
- Page 417 and 418:
etween vertices in different blocks
- Page 419 and 420:
∞∑ ∑ ix i = ∞ i=0 i=0 x d d
- Page 421 and 422:
Generating functions are useful for
- Page 423 and 424:
Thus, u n = (n − 1) u n−2 . The
- Page 425 and 426:
f(x) a c b Figure 12.3: Illustratio
- Page 427 and 428:
need to argue that no other sequenc
- Page 429 and 430:
1. How large must δ be if we wish
- Page 431 and 432:
Exercise 12.40 We are given the pro
- Page 433 and 434:
Index 2-universal, 240 4-way indepe
- Page 435 and 436:
Lagrange, 423 Law of large numbers,
- Page 437 and 438:
References [AK] Sanjeev Arora and R
- Page 439:
[MR95b] [MU05] [MV10] Rajeev Motwan