opstilling af regnef..

Repetition 3
af Matematik 0‐B Efterår 2012
Opstilling af regneforskrifter
Grafiske fremstillinger
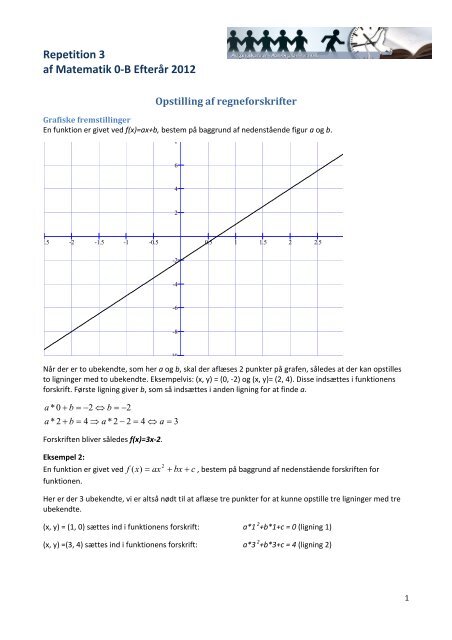
En funktion er givet ved f(x)=ax+b, bestem på baggrund af nedenstående figur a og b.
8
6
4
2
2.5 -2 -1.5 -1 -0.5 0.5 1 1.5 2 2.5
-2
-4
-6
-8
Når der er to ubekendte, som her a og b, skal der aflæses 2 punkter på grafen, således at der kan opstilles
to ligninger med to ubekendte. Eksempelvis: (x, y) = (0, ‐2) og (x, y)= (2, 4). Disse indsættes i funktionens
forskrift. Første ligning giver b, som så indsættes i anden ligning for at finde a.
a *0 + b = −2
⇔ b = −2
a * 2 + b = 4 ⇒ a * 2 − 2 = 4 ⇔ a = 3
Forskriften bliver således f(x)=3x‐2.
10
Eksempel 2:
En funktion er givet ved
funktionen.
2
f ( x)
= ax + bx + c , bestem på baggrund af nedenstående forskriften for
Her er der 3 ubekendte, vi er altså nødt til at aflæse tre punkter for at kunne opstille tre ligninger med tre
ubekendte.
(x, y) = (1, 0) sættes ind i funktionens forskrift: a*1 2 +b*1+c = 0 (ligning 1)
(x, y) =(3, 4) sættes ind i funktionens forskrift: a*3 2 +b*3+c = 4 (ligning 2)
1

Repetition 3
af Matematik 0‐B Efterår 2012
(x, y)= (‐1, 4) sættes ind i funktionens forskrift: a*(‐1) 2 +b*(‐1)+c =4 (ligning 3)
c isoleres i ligning 1 og sættes ind i ligning 2: c =‐ a‐b, 9a+3b‐a‐b =4
b isoleres i den ”nye” ligning 2: 2b =4‐8a b=2 – 4a
og indsættes i ligning 3 sammen med c fra ligning1: a‐(2‐4a)‐a‐(2‐4a) =4
a+4a‐a+4a =4+2+2, 8a=8, a=1, b=2‐4*1=‐2, c=‐(1+(‐2))=1
18
16
14
12
10
8
6
4
2
-2.5 -2 -1.5 -1 -0.5 0.5 1 1.5 2 2.5 3 3.5 4 4.5
Forskriften bliver således: f(x) = x 2 – 2x +1
Eksponentialfunktioner:
x
Eksempel: En funktion f er givet ved f ( x)
= b * a , samt at f(2)=3 og f(5) =24.
Bestem en regneforskrift for f.
Ovenstående opgave er en typisk eksamensopgave! Der findes i en del forskellige varianter. For at løse
opgaven opstilles to ligninger med to ubekendte:
Ligning 1: 24 = b*a 5
Ligning 2: 3 = b*a 2
De to ligninger divideres med hinanden således at b forsvinder: 8 = a 3 hvilket medfører at a = 2
Dette indsættes i ligning2 for at finde b: 3 = b*2 2 hvilket medfører at b = ¾
3 x
Regneforskriften bliver således: f ( x)
= * 2
4
2

Repetition 3
af Matematik 0‐B Efterår 2012
Eksempel 2:
a
En funktion f er givet ved f ( x)
= b * x , samt at f(‐1)=‐5 og f ’(‐1) =15.
Bestem en regneforskrift for f.
Igen skal der opstilles to ligninger med to ubekendte, men bemærk, at det er f ’(x) der er angivet som det
ene punkt. Det er en god ide at starte med at finde den.
f '( x)
= ab * x
a−1
Herefter opstilles de to ligninger:
Ligning 1: 15 =a b*(‐1) a‐1
Ligning 2: ‐5= b*(‐1) a
De to ligninger divideres med hinanden således at b forsvinder: ‐3 = a*(‐1) a‐1‐a , hvilket medfører at
‐a = ‐3 eller at a = 3. Dette indsættes i ligning2 for at finde b: ‐5 = b*(‐1) 3 hvilket medfører at b = 5
Regneforskriften bliver således:
f ( x)
= 5* x
3
Regression
Lineære udviklinger
Den lineære funktion f(x) = ax + b kaldes også for en lineær udvikling. Man taler om en lineær udvikling når
man bruger den lineære funktion til at beskrive eller opstille en model for en række måledata, der
tilsyneladende ligger på en ret linje.
Brug af TI­89 til lineær regression
Eksempel: Længden af delfiner
Alder (år) 1 2 3 4 5 6 7 8 9
Længde (cm) 211 249 276 321 359 390 440 465 500
Start med at tænde lommeregneren tryk derefter på knappen ”APPS” og vælg ”Data/Matrix” og vælg
”NEW”.
I vinduet vælges følgende: Type: Data; Folder: Main; Variable: her gives listen et navn ex. y, eller abc eller x
Derefter kommer der et skærmbillede op med ”c1”, ”c2”, ”c3” osv. Udfylde ”c1” med dine x‐værdier og din
”c2”, med de tilhørende y‐værdier. I delfin eksemplet er x‐værdierne fra 1 – 9 og y‐værdierne fra 211 – 500.
Kontroller at de rigtige y‐værdier står ud for de tilhørende x‐værdier.
Tryk nu på ”F5” og under calculation type ”5: LinReg”.
Der dukker nu et nyt skærmbillede frem, hvor du i første ”firkant” skal skrive ”c1” og i næste ”c2”. I næste
felt er det en god ide at vælge y1(x) og der skal stå NO ud for ”Use freq” og intet i de næste felter. Tryk nu
enter – nu har lommeregneren fundet hældningskoefficineten a = 36, 6833 og b = 173,361. Ud over det
3

Repetition 3
af Matematik 0‐B Efterår 2012
angiver den to andre værdier r = 0,9976 og r 2 = 0,9988. r står for korrelationskoefficient og r 2 står for
forklaringsgrad , begge disse værdier skal være så tæt på 1 som muligt for at den valgte model er så tæt på
det oprindelige datasæt som muligt.
I kan se funktionen under ”grafvinduet”. Tryk ”home”, vælg lysegrøn knap og F1. Under y1 står funktionen
og I kan få den tegnet. I kan også se værdierne under ”tabel”. I kan finde ud af, hvad værdien er når
delfinen er 0 år, x = 20, ved at trykke på Home og skrive ”y1(20)” så står der 907,02, dvs. 9 meter og 7 cm.
og I kan finde ud af hvornår en delfin er 6m og 30 cm lang ved at trykke ”solve(y1(x)=630,x)” så står der x =
12,448 dvs. 12 år og (0,448*12 mrd) 5 måneder.
Eksponentielle udviklinger
En funktion f(x) = b*a x , kaldes en eksponentiel udvikling, hvor a> 0, a≠ 1 og b>0.
Brug af TI­89 til eksponentiel regression
Eksempel: Bankers gebyrindtægt
Hvert år opgøres de danske bankers samlede nettogebyrindtægt for 1. halvår, her kaldet DBN. Tabellen
viser DBN for hvert af årene i perioden 2002‐2006.
År 2002 2003 2004 2005 2006
DBN (mia. kr.) 6,697 7,160 8,137 8,408 10,538
I en model antages det, at DBN (mia. kr.) som funktion af tiden x (antal år efter 2002) med god tilnærmelse
kan beskrives ved en eksponentiel udvikling f.
År 0 1 2 3 4
DBN (mia. kr.) 6,697 7,160 8,137 8,408 10,538
Udfyld listerne som beskrevet tidligere, husk at brug ”Del” til at slette evt. overflødige punkter i listerne.
Tryk nu på ”F5” og gå ved hjælp af pilene ned til ”4:ExpReg”.
Der dukker nu et nyt skærmbillede frem, hvor du i første ”firkant” skal skrive ”c1” og i næste ”c2”. I næste
felt er det en god ide at vælge y1(x) og der skal stå NO ud for ”Use freq” og intet i de næste felter. Tryk nu
enter – nu har lommeregneren fundet grundtallet a = 1,11264 og begyndelsesværdien
b = 6,5318. BEMÆRK at lommeregneren bytter om på ”vores brug af” a og b. Jeg synes det er lettere at
aflæse tallene, når jeg trykker på ”home” og går ud i graf vinduet. f(x) = 6,532*1,112 x
Potensielle udviklinger
En funktion f kaldes for en potensudvikling, hvis f har en forskrift på formen:
f(x) = b* x a og x > 0
Tallet a kaldes for potensudviklingens eksponent. Tallet b er funktionsværdien i 1, da
f(1) = b* 1 a = b * 1 = b
4

Repetition 3
af Matematik 0‐B Efterår 2012
Eksempel: Muslingeskaller
For muslinger på havbunden i Arktis har man fundet sammenhørende værdier af muslingens alder og
muslingeskallens længde som vist i tabellen.
alder (år) 0,9 2,0 6,0 6,9 9,9 10,7 14,0 15,9
længde (cm) 1,1 2,0 4,1 4,5 5,5 5,9 6,7 7,3
I en model antages det, at muslingeskallens længde som funktion af muslingens alder er en funktion af
typen L(t) =bt a ,
hvor L er skallens længde (målt i cm), og t er muslingens alder (målt i år).
a) Benyt tabellens data til at bestemme tallene a og b.
b) Benyt modellen til at bestemme længden af skallen for en musling, der er 24 år gammel.
TI‐89: Udfyld listerne som beskrevet tidligere, husk at brug ”Del” til at slette evt. overflødige punkter i
listerne.
Tryk nu på ”F5” og gå ved hjælp af pilene ned til ”8:PowerReg”.
b = 1,23 og a = 0,6548, så funktionen kommer til at hedde L(t) = 1,23*t 0,6548
En musling er der 24 år gammel er (y1(24) = 9,85) 9,85 cm lang.
OPGAVER
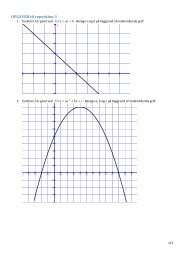
1. funktion f er givet ved f ( x)
= ax + b . Beregn a og b på baggrund af nedenstående graf:
y
8
6
4
2
3 -2 -1 1 2 3 4 5 6
-2
-4
5

Repetition 3
af Matematik 0‐B Efterår 2012
2
2. funktion f er givet ved f ( x)
= ax + bx + c . Beregn a, b og c på baggrund af nedenstående graf:
9
8
7
6
5
4
3
2
1
.5 -2 -1.5 -1 -0.5 0.5 1 1.5 2 2.5 3 3.5 4 4.5 5 5.5 6
-1
-2
-3
3. En funktion f er givet ved
f *
x
( x)
= b a . Beregn a og b på baggrund af nedenstående figur.
y
9
8
7
6
5
4
3
2
1
.5 -2 -1.5 -1 -0.5 0.5 1 1.5
-1
3 2
4. En funktion f er givet ved forskriften f ( x)
= x + bx + c . Grafen for funktionen er vist på figuren.
Bestem ved anvendelse af grafen konstanterne b og c.
6

Repetition 3
af Matematik 0‐B Efterår 2012
6
4
2
-2 -1 1 2 3 4
-2
-4
5. En funktion f er givet ved f *
6. En funktion f er givet ved f *
x
7. En funktion f er givet ved f ( x)
= b * a , samt at f(2)=48 og f ’(2) =48ln(4). Bestem en
regneforskrift for f.
a
8. En funktion f er givet ved forskriften f ( x)
= b * x , samt at f(2)=5 og f(4) =40. Bestem en
regneforskrift for f.
9.
a
( x)
= b x . Beregn a og b, når der gælder at f(2)=3 og f ’(2) =3.
x
( x)
= b a . Beregn a og b, når der gælder at f(5)=18 og f(3) =2.
7

Repetition 3
af Matematik 0‐B Efterår 2012
10.
11.
8