Mathematik III für Bauwesen 1. Übungsblatt

Mathematik III für Bauwesen
1. Übungsblatt
Fachbereich Mathematik Wintersemester 2010/2011
Prof. Dr. Roland Pulch 25. Oktober 2010
Andreas Gärtner
Florian Seib
Gruppenübung
Aufgabe G1 (Richtungsfeld)
Eine gewöhnliche Differentialgleichung 1. Ordnung der Gestalt y ′ = f (x, y) schreibt für jeden Punkt (x, y) einer Lösungskurve
y(x) eine Steigung f (x, y) vor. Eine Veranschaulichung der Differentialgleichung ist somit durch eine Skizze
des korrespondierenden Richtungsfeldes möglich: Hierzu zeichnet man in einigen Punkten (x, y) ein kurzes Geradenstück
(das als Linienelement bezeichnet wird) mit der Steigung f (x, y). Eine Lösungskurve y = y(x) muss so durch das
Richtungsfeld laufen, dass das Linienelement in jedem Punkt (x, y(x)) tangential an die Kurve ist.
Für eine Zeichnung des Richtungsfeldes ist es günstig, wenn man sich für einige Werte c ∈ überlegt, wo die Linienelemente
mit Steigung c liegen. Diese sogenannten Isoklinen („Kurven mit gleicher Steigung der Linienelemente“) erhält
man aus der Gleichung
Gegeben sei die gewöhnliche Differentialgleichung
(a) Berechnen Sie die Isoklinen.
f (x, y) = c.
y ′ = 1 + x + y.
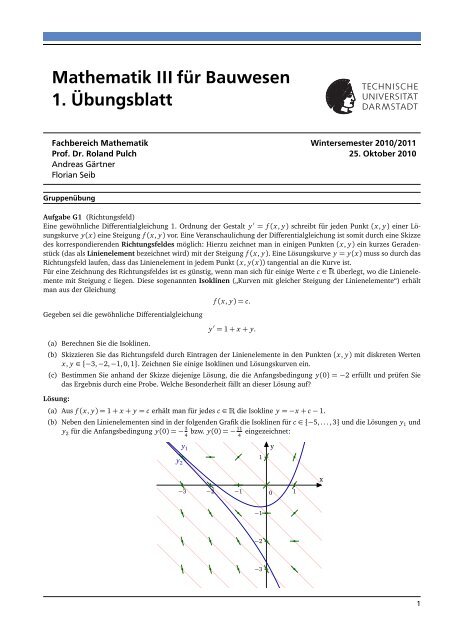
(b) Skizzieren Sie das Richtungsfeld durch Eintragen der Linienelemente in den Punkten (x, y) mit diskreten Werten
x, y ∈ {−3, −2, −1, 0, 1}. Zeichnen Sie einige Isoklinen und Lösungskurven ein.
(c) Bestimmen Sie anhand der Skizze diejenige Lösung, die die Anfangsbedingung y(0) = −2 erfüllt und prüfen Sie
das Ergebnis durch eine Probe. Welche Besonderheit fällt an dieser Lösung auf?
Lösung:
(a) Aus f (x, y) = 1 + x + y = c erhält man für jedes c ∈ die Isokline y = −x + c − 1.
(b) Neben den Linienelementen sind in der folgenden Grafik die Isoklinen für c ∈ {−5, . . . , 3} und die Lösungen y 1 und
y 2 für die Anfangsbedingung y(0) = − 3
4
y 2
y 1
bzw. y(0) = − 11
4 eingezeichnet:
−3 −2 −1 0 1
1
−1
−2
−3
y
x
1

(c) Für y(0) = −2 ergibt sich die Lösung y(x) = −x − 2. Für diese Anfangsbedingung fällt der nichtlineare Teil der
allgemeinen Lösung weg.
Aufgabe G2 (Trennung der Veränderlichen)
Lösen Sie die folgenden Anfangswertprobleme durch Trennung der Veränderlichen und verifizieren Sie Ihre Lösung
anschließend durch Differenzieren.
(a) y ′ = y 4 , y(9) = − 1
3 ,
(b) y ′ = x y 2 + x, y(0) = 1.
Lösung:
(a) Mit Trennung der Veränderlichen erhalten wir die allgemeine Lösung der Differentialgleichung:
Aus der Anfangsbedingung y(9) =
gegeben durch:
d y
d x = y′ = y 4 d y
❀ “ = 1 · d x ”
y4
⇒
⇒
y −4 d y =
1d x
1
−3 y−3 = x + c, c ∈
1
−
⇒ y(x) = (−3(x + c)) 3 =
−1
3 3(9+c)
−1
3
3(x + c)
, c ∈ .
!
= − 1
folgt c = 0 und damit ist die Lösung des Anfangswertproblems
3
y(x) = −1
3 3x .
(b) Da y ′ = x y2 + x = x(y 2 + 1) ist, können wir die allgemeine Lösung der Differentialgleichung durch Trennung der
Veränderlichen berechnen und erhalten:
d y
d x = x(y2
1
+ 1) ⇒
y2
d y = xd x
+ 1
2 x
⇒ arctan(y) = + c, c ∈
2
2 x
⇒ y(x) = tan + c , c ∈ .
2
Aus y(0) = tan(c) ! = 1 folgt c = arctan(1) = π
und damit ist die Lösung des Anfangswertproblems gegeben durch:
4
2 x
y(x) = tan
2
π
+ .
4
Aufgabe G3 (Inhomogene lineare Differentialgleichung I)
Gegeben sei das folgende Anfangswertproblem einer inhomogenen linearen Differentialgleichung 1. Ordnung
y ′ x + y = 1 + x (x > 0), y(1) = 2.
(a) Lösen Sie die korrespondierende homogene Differentialgleichung, d.h. bestimmen Sie die Menge aller Lösungen.
(b) Bestimmen Sie die spezielle Lösung des Anfangswertproblems der inhomogenen Differentialgleichung.
Lösung:
(a) Die korrespondierende homogene Differentialgleichung lautet y ′ x + y = 0. Wir erhalten die homogene Lösung
durch Trennung der Veränderlichen:
d y y
= −
d x x ⇒
1 1
d y = − d x
y x
⇒ ln |y| = − ln |x| + c = ln(|x| −1 ) + c, c ∈
⇒ yh(x) = 1
x · (±ec ), c ∈ bzw. yh(x) = C · 1
,
x
C ∈ .
2

(b) Für die Bestimmung einer speziellen Lösung nutzen wir die Variation der Konstanten:
y s(x) = C(x) 1
x ,
⇒ y ′
s (x) = C ′ (x) 1
x
−1
+ C(x) .
x 2
Setzen wir dies in die inhomogene Differentialgleichung ein, erhalten wir:
C ′ (x) 1
x
− C(x) 1
x
2 = y′
s
Daraus ergibt sich dir Differentialgleichung:
C ′ (x) 1
x
− C(x) 1
x
1
(x) = −ys(x) + 1 + x =
x
1
−C(x)
x
1
+ 1 + x .
x
1 1 + x
= −C(x) + 2 x 2 x ⇔ C ′ (x) = 1 + x
Damit ist C(x) = x + x2
2 + ˜C mit ˜C ∈ und mit ys(1) = 1 + 1
2 + ˜C ! = 2 folgt, dass ys(x) = x + x2
2
spezielle Lösung des Anfangswertproblems ist.
Hausübung
1 −1 + · x die
2
Aufgabe H1 (Anfangswertproblem von Differentialgleichung) (7 Punkte)
Lösen Sie das folgende Anfangswertproblem einer gewöhnlichen Differentialgleichung
y ′
y
=
1 + 1 , y(0) = 1.
x
2
Lösung: Mit Trennung der Veränderlichen erhalten wir die allgemeine Lösung der Differentialgleichung:
d y
d x =
1
1 + 1
2 x
Aus der Anfangsbedingung y(0) = (ln(1) + 1
obige Anfangswertproblem:
y ⇒
1
d y =
y
1
1 + 1 d x
x
2
⇒ 2y 1
2 = 2 ln |1 + 1
x| + c, c ∈
2 c)2 = ( 1
2
⇒ y(x) = ln |1 + 1 1
x| +
2 2 c 2
, c ∈ .
2 c)2 ! = 1 folgt c = ±2 und damit lösen die folgenden Funktionen das
y ±(x) = ln |1 + 1
2 x| ± 1 2
.
Aufgabe H2 (Inhomogene lineare Differentialgleichung II) (7 Punkte)
Gegeben sei die folgende inhomogene lineare Differentialgleichung
y ′ + cos(x) y = 3 cos(x).
(a) Lösen Sie die korrespondierende homogene Differentialgleichung.
(b) Lösen Sie die inhomogene Differentialgleichung durch Variation der Konstanten.
Bestimmen Sie in beiden Fällen die Menge aller Lösungen.
Lösung:
(a) Wir lösen die korrespondierende homogene Differentialgleichung y ′ = − cos(x) y durch Trennung der Veränderlichen:
d y
= − cos(x) y
d x
⇒
1
d y = −
y
cos(x)d x
⇒ ln |y| = − sin(x) + c, c ∈
⇒ y h(x) = C · e − sin(x) , C ∈ .
3

(b) Für die Bestimmung einer speziellen Lösung nutzen wir die Variation der Konstanten:
y s(x) = C(x) · e − sin(x) ,
⇒ y ′
s (x) = C ′ (x) · e − sin(x) − C(x) · e − sin(x) cos(x).
Setzen wir dies in die inhomogene Differentialgleichung ein, erhalten wir:
C ′ (x) · e − sin(x) − C(x) · e − sin(x) cos(x) = y ′
s (x) = − cos(x) y s(x) + 3 cos(x) = − cos(x) C(x) · e − sin(x) + 3 cos(x).
Daraus ergibt sich dir Differentialgleichung:
C ′ (x) = 3 cos(x) · e sin(x)
Damit ist C(x) = 3e sin(x) + ˜C mit ˜C ∈ und y s(x) = 3e sin(x) · e − sin(x) = 3 eine spezielle Lösungen der Differentialgleichung.
Die Menge aller Lösungen der inhomogenen Differentialgleichung wird also von allen Funktionen der
Form y(x) = y s(x) + y h(x) = 3 + C · e − sin(x) mit C ∈ gebildet.
Aufgabe H3 (Klassifikation von Differentialgleichungen) (6 Punkte)
Klassifizieren Sie die folgenden Differentialgleichungen nach den Kategorien gewöhnlich oder partiell sowie linear oder
nichtlinear. Stellen Sie auch jeweils die Ordnung der Differentialgleichung fest.
1. y ′′ + x y 2 + x 3 = 0
2. y 2 · z x x + 2x y · z x y + x 2 · z y y = 0
3. y ′ = sin(y) + x 2
4. z 2 · z x + x · z y = 1
x 2 + y 2
5. cos(x)y ′′′ + x 2 y ′ = sin(x)
6. y ′ = y + y
x 2 + x
Lösung:
1. gewöhnlich, nichtlinear, 2. Ordnung
2. partiell, linear, 2. Ordnung
3. gewöhnlich, nichtlinear, 1. Ordnung
4. partiell, nichtlinear, 1. Ordnung
5. gewöhnlich, linear, 3. Ordnung
6. gewöhnlich, linear, 1. Ordnung
4