Trigonometrische Funktionen - Mathe-total.de

Trigonometrische Funktionen
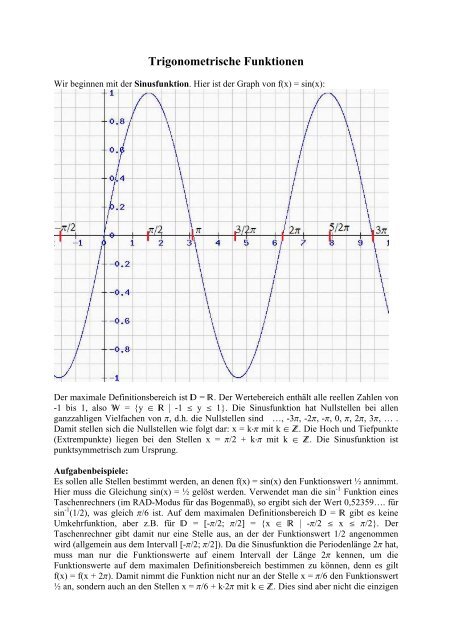
Wir beginnen mit der Sinusfunktion. Hier ist der Graph von f(x) = sin(x):
Der maximale Definitionsbereich ist D = R. Der Wertebereich enthält alle reellen Zahlen von
-1 bis 1, also W = {y œ R | -1 § y § 1}. Die Sinusfunktion hat Nullstellen bei allen
ganzzahligen Vielfachen von p, d.h. die Nullstellen sind …, -3p, -2p, -p, 0, p, 2p, 3p, … .
Damit stellen sich die Nullstellen wie folgt dar: x = kÿp mit k œ Z. Die Hoch und Tiefpunkte
(Extrempunkte) liegen bei den Stellen x = p/2 + kÿp mit k œ Z. Die Sinusfunktion ist
punktsymmetrisch zum Ursprung.
Aufgabenbeispiele:
Es sollen alle Stellen bestimmt werden, an denen f(x) = sin(x) den Funktionswert ½ annimmt.
Hier muss die Gleichung sin(x) = ½ gelöst werden. Verwendet man die sin -1 Funktion eines
Taschenrechners (im RAD-Modus für das Bogenmaß), so ergibt sich der Wert 0,52359…. für
sin -1 (1/2), was gleich p/6 ist. Auf dem maximalen Definitionsbereich D = R gibt es keine
Umkehrfunktion, aber z.B. für D = [-p/2; p/2] = {x œ R | -p/2 § x § p/2}. Der
Taschenrechner gibt damit nur eine Stelle aus, an der der Funktionswert 1/2 angenommen
wird (allgemein aus dem Intervall [-p/2; p/2]). Da die Sinusfunktion die Periodenlänge 2p hat,
muss man nur die Funktionswerte auf einem Intervall der Länge 2p kennen, um die
Funktionswerte auf dem maximalen Definitionsbereich bestimmen zu können, denn es gilt
f(x) = f(x + 2p). Damit nimmt die Funktion nicht nur an der Stelle x = p/6 den Funktionswert
½ an, sondern auch an den Stellen x = p/6 + kÿ2p mit k œ Z. Dies sind aber nicht die einzigen

Stellen, denn der Funktionswert ½ wird alleine auf dem Intervall I = [0; 2p] =
{x œ R | 0 § x § 2p} zweimal angenommen, siehe Graph der Sinusfunktion:
Die zweite Stelle in dem Intervall I liegt bei x = p - p/6 = 5/6p, denn f(p/6) = f(5/6p) = ½ .
Also gilt f(x) = sin(x) = ½ für x = p/6 + kÿ2p oder x = 5/6p + kÿ2p mit k œ Z.
Betrachtet man die Funktion f(x) = sin(2x), so hat diese nur noch die Periodenlänge p:

Die Funktion f(x) = sin(1/2x) hat die Periodenlänge 4p:
Allgemein hat f(x) = cÿsin(ax) (für a und c ungleich Null) die Periodenlänge 2p/|a|. Der
Wertebereich ist dann W = [-|c|; |c|], womit der größtmögliche Funktionswert den Wert |c| hat
(|c| wird in physikalischen Anwendungen auch als Amplitude bezeichnet). Verwendet man
statt c den Faktor -c, so bewirkt dies eine Spiegelung der Kurve an der x-Achse (was auch
allgemein gilt, wenn man eine Funktionsgleichung mit -1 multipliziert).
Beispielsweise hat g(x) = 5sin(px) die Periodenlänge 2p/p = 2 und den größtmöglichen
Funktionswert 5.
Nun kann man die Kurve auch verschieben. h(x) = sin(x - b) bewirkt für positive b eine
Verschiebung der Kurve von f(x) = sin(x) um b Einheiten nach rechts (analog zur
Verschiebung von Parabeln). Dagegen wäre die Kurve von g(x) = sin(x) + d für positive d
nach oben und für negative d nach unten verschoben.
Wenn man alles kombiniert, würde man allgemein
erhalten.
f(x) = cÿsin(ax - b) + d

Es folgt der Graph von h(x) = sin(x - p):
Hier wurde der Graph der Funktion f(x) = sin(x) um p nach rechts verschoben. Die Funktion h
ist identisch mit der Funktion i(x) = -sin(x) (deren Graph sich durch Spiegelung des Graphen
von f an der x-Achse ergibt).
Als nächstes ist noch der Graph von j(x) = sin(2x - p) zu sehen:

Der Graph von j ergibt sich aus dem Graph von k(x) = sin(2x) durch Verschiebung um p/2
nach rechts oder aus dem Graph von f, wenn man diesen um p nach rechts verschiebt und
dann mit dem Faktor a = 2 (in x-Richtung) staucht, denn j(x) = sin(2x - p) = sin(2(x - p/2)).
Somit gibt es zwei Möglichkeiten der Konstruktion von j mit Hilfe von f.
Kommen wir als nächstes zur Kosinusfunktion: f(x) = cos(x). Diese kann man über die
Sinusfunktion konstruieren, denn cos(x) = sin(x + p/2).
Es folgt der Graph der Kosinusfunktion:

Die Kosinusfunktion ist achsensymmetrisch zur y-Achse und hat ihre Nullstellen bei
x = p/2 + kÿp (den Extremstellen bzw. Hoch- und Tiefstellen der Sinusfunktion) und die
Extremstellen der Kosinusfunktion liegen bei x = kÿp (jeweils für k œ Z), also den Nullstellen
der Sinusfunktion.
Alles Übrige kann man nun analog auch auf die Kosinusfunktion übertragen.
Aufgabenbeispiel:
Es soll die Gleichung cos(x) = ½ gelöst werden.
cos(x) = ½ | cos -1
x = p/3
Anstatt p/3 gibt der Taschenrechner 1,0472… aus. Wir haben nun eine Lösung. Wegen der
Periodenlänge von 2p haben wir weitere Lösungen an den Stellen x = p/3 + kÿ2p mit k œ Z.
Nun gibt es aber alleine im Intervall I = [0; 2p] noch eine Lösung, was man an der folgenden
Grafik sieht (Graph der Kosinusfunktion f(x) = cos(x) unten). Die weitere Lösung im Intervall
I ist x = 2p - p/3 = 5/3p. Damit ergeben sich alle Lösungen bzw. die Lösungsmenge:
L = {x œ R | x = p/3 + kÿ2p oder x = 5/3p + kÿ2p mit k œ Z}

Als letztes kommen wir zur Tangensfunktion: f(x) = tan(x). Hier gilt tan(x) = sin(x)/cos(x).
Es folgt der Graph der Tangensfunktion f(x) = tan(x):

Damit hat der die Tangensfunktion dieselben Nullstellen wie die Sinusfunktion. Zusätzlich
hat die Tangensfunktion damit Definitionslücken (die Polstellen sind) bei den Nullstellen der
Kosinusfunktion: D = R \ {x | x = p/2 + kÿp mit k œ Z}. Der Wertebereich ist gleich R.
Bemerkung:
Man kann die trigonometrischen Funktionen am Einheitskreis definieren. Dies ist ein Kreis
der mit dem Radius einer Längeneinheit (1cm, oder 1dm, …). Wir haben den Kreis in ein
Koordinatensystem gezeichnet mit dem Mittelpunkt im Ursprung. Malt man in diesen Kreis
ein rechtwinkliges Dreieck, mit dem Ursprung und dem Punkt (1; 0) als Eckpunkte und einem
weiteren Eckpunkt P auf dem Kreis (womit eine Kathete auf der x-Achse und eine parallel zur
y-Achse verläuft), so kann man an den Längen der Katheten die Werte von sin(x) und cos(x)
ablesen (siehe Grafik). Im Bogenmaß ist x die Länge des Kreisbogens von Punkt (1; 0) bis
zum Punkt P ist. Den Wert von tan(x) kann man an der Länge des Tangentenstückes der
Tangente im Punkt (1; 0) ablesen, welches vom Punkt (1; 0) bis zum Schnittpunkt der
Verlängerung der Hypotenuse mit der Tagente verläuft. Diese Beziehung ergibt sich über den
Strahlensatz, denn sin(x)/cos(x) = tan(x)/1.
Da der Umfang des Kreises U = 2pr = 2p (LE) beträgt, entsprechen 2p im Bogenmaß 360° im
Gradmaß. An dem Einheitskreis kann man erkennen, dass sin(0) = 0 und cos(0) = 1 ist,
während sin(p/2) = 1 und cos(p/2) = 0 ist.
Wendet man Pythagoras an, dann ergibt sich eine Beziehung zwischen sin und cos (mit
sin 2 (x) = (sin(x)) 2 ):
sin 2 (x) + cos 2 (x) = 1