Splines

Institut für Geometrie 

Abteilung für Geometrie im Bauwesen 

und im Scientific Computing 

Prof. Dr. H. Pottmann 

GEOMETRIE 

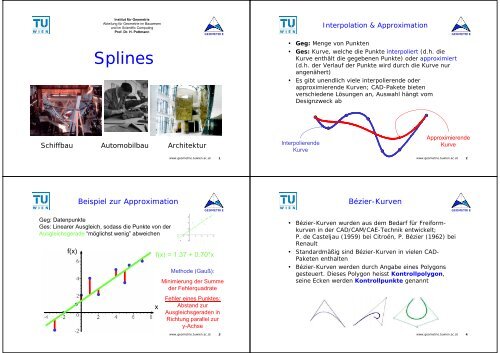
Interpolation & Approximation 

GEOMETRIE 

Splines 

• Geg: Menge von Punkten 

• Ges: Kurve, welche die Punkte interpoliert (d.h. die 

Kurve enthält die gegebenen Punkte) oder approximiert 

(d.h. der Verlauf der Punkte wird durch die Kurve nur 

angenähert) 

• Es gibt unendlich viele interpolierende oder 

approximierende Kurven; CAD-Pakete bieten 

verschiedene Lösungen an, Auswahl hängt vom 

Designzweck ab 

Schiffbau Automobilbau Architektur 

Interpolierende 

Kurve 

Approximierende 

Kurve 

www.geometrie.tuwien.ac.at 

1 


2 

Beispiel zur Approximation 

Bézier-Kurven 

GEOMETRIE 

GEOMETRIE 

Geg: Datenpunkte 

Ges: Linearer Ausgleich, sodass die Punkte von der 

Ausgleichsgerade “möglichst wenig” abweichen 

f(x) 

f(x) = 1.37 + 0.70*x 

x 

Methode (Gauß): 

Minimierung der Summe 

der Fehlerquadrate 

Fehler eines Punktes: 

Abstand zur 

Ausgleichsgeraden in 

Richtung parallel zur 

y-Achse 

• Bézier-Kurven wurden aus dem Bedarf für Freiformkurven 

in der CAD/CAM/CAE-Technik entwickelt; 

P. de Casteljau (1959) bei Citroën, P. Bézier (1962) bei 

Renault 

• Standardmäßig sind Bézier-Kurven in vielen CAD- 

Paketen enthalten 

• Bézier-Kurven werden durch Angabe eines Polygons 

gesteuert. Dieses Polygon heisst Kontrollpolygon, 

seine Ecken werden Kontrollpunkte genannt 


3 


4

Grad einer Bézier-Kurve 

Grad einer Bézier-Kurve 

GEOMETRIE 

GEOMETRIE 

• Eine Bézier-Kurve mit n+1 

Kontrollpunkten besitzt den Grad n 

(= Grad der in der mathematischen 

Beschreibung auftretenden Polynome) 

• 2 Kontrollpunkte Grad 1 Bezier- 

Kurve ist Verbindungsstrecke der 

beiden Kontrollpunkte 

• Grad 1 

– lineare Bézier-Kurve 

• Grad 2 

– quadratische Bézier- 

Kurve 

b 1 

• 3 Kontrollpunkte Grad 2 Bezier- 

Kurve ist Parabelbogen; Kontrollpunkte: 

T 2 

Endpunkte b 0 b 2 und Schnittpunkt b 1 

der Tangenten T 0 

, T 2 

in den Endpunkten b 0 b 2 

• Grad 3 

– kubische Bézier-Kurve 

T 0 6 


5 


Geometrischer Algorithmus 

zur Konstruktion von Bezier-Kurven 

GEOMETRIE 

Fadenkonstruktion einer Parabel 

GEOMETRIE 

• Für eine quadratische Bezier-Kurve 

(Parabelbogen) ist der Algorithmus 

die Fadenkonstruktion einer 

Parabel 

• Wird später auf höhere Grade 

verallgemeinert (Algorithmus von 

de Casteljau) 

Geg: 2 Linienelemente (b 0 , T 0 ), 

(b 2 , T 2 ) einer Parabel 

Ges: weitere Linienelemente 

(d.h. Punkte mit Tangenten) 

T 

T 2 

Konstruktion für t = 0.25, 0.5, 

0 0.75 

b 0 

b 1 

b 2 


7 

0 t 1 


8



GEOMETRIE 

GEOMETRIE 

Methode: Übertragen von Teilverhältnissen 

b 11 (0.25) 

b 01 (0.75) 

b 01 (0.5) 

b 11 (0.25) 

b 01 (0.25) 

b 0 

2 

(0.25) 

Kurvenpunkt 

b 0 

b 1 

b 2 

b 01 (0.25) 

b 02 ... 

Kurven 

punkt 

b 11 (0.5) 

b 0 

b 1 

b 2 

b 11 (0.75) 

TV(b 0 , b 1 , b 0 1 ) = TV(b 1 , b 2 , b 1 1 ) = TV(b 0 1 , b 1 1 , b 0 2 ) 


9 


10 

Algorithmus von de Casteljau 

GEOMETRIE 

Ist eine Verallgemeinerung der Fadenkonstruktion der Parabel. 

Teilverhältnisübertragen liefert Polygone mit absteigender 

Eckenzahl bis schliesslich nur noch der Kurvenpunkt 

übrigbleibt. 

b 

1 b 1 2 

b 1 

Geg: Kontrollpunkte 

b 

2 

0 

b 

2 

b 0 ,...,b n 

1 

Ges: Punkte der Bezier- 

Kurve n-ten Grades 

Jeder Punkt besitzt einen 

“Parameter” t aus dem 

Intervall [0,1]: 

t=0 entspricht b 0 

b 0 

1 

b 0 

b 0 

3 

0 t 1 

b 3 

b 2 

1 

de Casteljau-Schema: 

Algorithmus von de Casteljau 

t=1 entspricht b 

www.geometrie.tuwien.ac.at 11 

www.geometrie.tuwien.ac.at 12 

n 

b 0 

b 1 b 0 

1 

b 2 b 1 

1 

b 0 

2 

b 3 b 2 

1 

b 1 

2 

b 0 

3 

b 0 

GEOMETRIE 

b 1 

b 2 

b 0 

1 

b 0 

2 

b 1 

1 

b 0 

3 

0 t 1 

b 1 

2 

b 3 

b 2 

1

Beispiele von Bézier-Kurven 

Bézier-Kurven – Eigenschaften 

Kurven vom Grad 3 

GEOMETRIE 

Endpunktinterpolation + Tangenteneigenschaft 

(endpoint interpolation): 

GEOMETRIE 

b 0 

Eine Bézier-Kurve interpoliert den ersten und den 

letzten Punkt des Kontrollpolygons und besitzt dort 

die erste bzw. letzte Strecke des Kontrollpolygons 

als Tangente. 

Kurven vom Grad 4 

Kontrollpolygon 

b n 


13 

Linienelement 

Bézier-Kurve 

Linienelement 


14 

Wiederholung: 

Konvexe Hülle 

konvexer Bereich ist eine Punktmenge, welche die 

Verbindungsstrecken aller ihrer Punktepaare enthält 

GEOMETRIE 


Konvexe Hülle Eigenschaft (convex hull property): 

Eine Bézier-Kurve liegt in der konvexen Hülle ihres 

Kontrollpolygons. 

GEOMETRIE 

konvexe Hülle ist 

der “kleinste” 

konvexe Bereich, 

welcher eine 

gegebene (Punkt-) 

Menge enthält 


15 


16


GEOMETRIE 

Variationsreduzierende Eigenschaft in der Ebene [im Raum] 

(variation diminishing property): 

Geg: Bézier-Kurve, beliebige Gerade [Ebene] 

Eine Bézier-Kurve wechselt die Seite jeder beliebigen Gerade 

[Ebene] nicht öfter als das Kontrollpolygon. 


Lineare Präzision (linear precision): 

Liegen die Kontrollpunkte b 0 ,...,b n einer Bézier- 

Kurve kollinear (= auf einer Geraden), dann liegt 

die Bézier-Kurve auf der Strecke b 0 b n 

GEOMETRIE 

2 

Testgeraden 

1 

3 

3 


b n 

1 

2 

1 

3 

2 

Bézier-Kurve 

1 

b 0 


17 


18 

Unterteilung (subdivision): 

Gegeben sei eine Bézier- 

Kurve mit Kontrollpolygon 

(b 0 ,...,b n ) bzgl. [0,1]. 

Manchmal ist es notwendig, 

eine einzelne Bézier-Kurve 

so in zwei Teilstücke zu 

zerlegen, dass sie 

gemeinsam identisch sind 

zur Ausgangskurve. 

1. Unterteilungsalgorithmus 

von de Casteljau liefert auch 

die Kontrollpolygone 

(c 0 ,...,c n ) und (d 0 ,...,d n ) der 

Bézier-Kurve bzgl. der 

Intervalle [0,t] bzw. [t,1]. 



GEOMETRIE 

b 1 

b 2 

c 1 

c 2 

c 3 

d 1 

d 2 

b 3 

c 0 

b 0 Beispiel: n=3 

19 




(b 0 ,...,b n ) 

2. Wiederholte Unterteilung 

mit de Casteljau liefert eine 

rasch gegen die Kurve 

konvergierende 

Polygonfolge. 


b 0 


GEOMETRIE 

b 1 

b 2 

b 3 

d 0 

d 3 

20


3D-Bézier-Kurven 

GEOMETRIE 

GEOMETRIE 




(b 0 ,...,b n ) 

b 1 

b 2 

Geg: Kontrollpunkte 

im 3-Raum 

Ges: Bézier-Kurve 

b 2 

b 3 

Bézier- 

Kurve 

3. Durch Eckenabschneiden 

entstehen keine zusätzlichen 

Seitenwechsel 

⇒ Variationsreduzierende 

Eigenschaft gilt 

b 3 

b 0 

b 1 

b 0 


21 

Die Bézier-Kurve liegt in der konvexen Hülle 

ihres Kontrollpolygons (hier: Tetraeder) 



22 

Spline-Kurven 

Grad und Kontrollpunkte von Splines 

GEOMETRIE 

GEOMETRIE 

Bézier-Kurven sind durch das 

Kontrollpolygon bestimmt. 

Damit bewirkt die Änderung eines 

Kontrollpunktes eine Veränderung des 

gesamten Kurvenverlaufes (global). 

⇒ ungünstig für Designzwecke 

Eine mögliche Abhilfe: Kurven niegrigen 

Grades zu einer Kurve zusammensetzen 

⇒ Spline- Kurve, lokale Kontrolle, an den 

Segmenttrennstellen geeignete 

Übergangsbedingung (z.B. gemeinsame 

Tangente). 

• Viele Splinetypen (B-Spline, 

NURBS, “continuous Bezier” 

in formZ, interpolierende 

kubische Splines) sind aus 

Bezierkurven 

zusammengesetzt 

• Der Grad der Bezier- 

Segmente heißt Grad der 

Splinekurve 

• Die Kontrollpunkte des 

Splines sind oft von den 

Kontrollpunkten der 

Beziersegmente verschieden 


23 


24

Grad und Kontrollpunkte 

von B-Spline Kurven 

GEOMETRIE 

Spline-Kurven 

GEOMETRIE 

• kubische B-Spline Kurve 

mit B-Spline Kontrollpolygon 

Beispiel: 2 mögliche Kurven zum selben Kontrollpolygon 

Bézier-Kurve 

(Grad 13) 

• kubische B-Spline Kurve 

mit Kontrollpolygonen der 

kubische Beziersegmente 


25 

Kurve ist aus Parabelsegmenten mit 

tangentenstetigem Übergang zusammengesetzt. 

B-Spline 

(Grad 2) 


26 

B-Spline Kurven, NURBS 

B-Spline-Kurven wurden ins Computer Aided Design von J. Ferguson 

(1964) bei Boeing eingeführt. In CAD-Systemen taucht auch oft der 

Name NURBS (= Non-Uniform Rational B-Splines) auf. 

B-Spline-Kurve 

Grad 2 


Grad 3 

GEOMETRIE 

B-Spline Kurven 

• Eine B-Spline-Kurve vom Grad n besteht aus 

Bezier-Kurven vom Grad n, welche mit 

optimaler Glattheit zusammengesetzt sind 

– Grad 2: stetige Tangente 

– Grad 3: stetige Krümmung 

• Angabe: Kontrollpolygon, Grad, Knoten (hängt 

mit mathematischer Beschreibung zusammen, 

für Design kaum verwendbar) 

GEOMETRIE 


Grad 7 

(= Bézier) 


27 


28

B-Spline Kurven 

GEOMETRIE 

B-Spline-Kurven 

Eigenschaften 

GEOMETRIE 

• B-Spline-Kurven können offen oder geschlossen sein: 

– Bei einer geschlossenen B-Spline-Kurve wird ein 

geschlossenes Kontrollpolygon zur Gänze geglättet 

– Im offenen Modus hat ein geschlossenes Polygon 

einen Anfangspunkt und einen damit identischen 

Endpunkt; dort wird nicht geglättet 

• Bei offenen B-Spline Kurven: Endpunkte mit Tangenten 

werden durch das Kontrollpolygon angegeben 

• Kurve liegt in der konvexen Hülle des Kontrollpolygons 

geschlossen 

offen 

offen 

• Es gilt die variationsreduzierende 

Eigenschaft 


29 


30 

NURBS – Gewichte (weights) 

Kegelschnitte als NURBS 

GEOMETRIE 

GEOMETRIE 

• B-Spline-Kurven und somit auch die 

Bézier-Kurven sind Spezialfälle von 

NURBS (= Non-Uniform Rational B- 

Splines) 

• NURBS haben einen zusätzlichen 

Designparameter ⇒ Gewichte. 

• Standardmäßig sind alle Gewichte 

gleich 1, dann stimmt die NURBS- 

Kurve mit der gewöhnlichen B-Spline- 

Kurve überein 

• Das Erhöhen des Gewichtes eines 

Kontrollpunktes bewirkt, dass die 

Kurve zu diesem Kontrollpunkt 

hingezogen wird 

Multipliziert man die Gewichte aller 

Punkte mit demselben Faktor, so 

erhält man die ursprüngliche Kurve 

b 1 

w 1 

> 1 

w 1 

= 1 

0 < w 1 

< 1 

w 1 > 1 Hyperbelbogen 

w 1 = 1 Parabelbogen 

0 < w 1 < 1 Ellipsenbogen 

b 0 b 2 

Von den Kegelschnitten (Kreis, Ellipse, 

Parabel, Hyperbel) kann nur die Parabel 

als Bézier-Kurve (vom Grad 2) 

repräsentiert werden. 

Durch das Verwenden von Gewichten 

können alle Kegelschnittstypen als 

NURBS vom Grad 2 erhalten werden. 


31 


32

Tipps zum CAD Konstruieren 

mit Splinekurven 

GEOMETRIE 

Splines in der Architektur 

GEOMETRIE 

• Komplexe Kurvenformen mittels 

NURBS modellieren, 

Feinabstimmung durch 

Veränderung der Kontrollpunkte 

und der Gewichte 

Grand Arbour, 

Brisbane, Australia 


33 


34 

Unterteilungskurven 

(Subdivision curves) 

GEOMETRIE 

Chaikins Algorithmus 

GEOMETRIE 

• Grundideen der Unterteilung gehen 

zurück in die 40er Jahre als G. 

Rahm „corner cutting“ dazu 

verwendete glatte Kurven zu 

beschreiben 

• stationäres Unterteilungsschema, d.h. in jedem 

Iterationsschritt k=1,2,… wird dieselbe Methode 

(corner cutting) angewendet 

• für k ∞ erhält man so eine quadratische 

B-Spline Kurve 

• Anwendungen im CAD, 

geometrischen Modellieren und in 

der Computergraphik 


35 


36



GEOMETRIE 

GEOMETRIE 

P 1 P 2 

P 3 

P 4 

Q 1 R 1 R 3 

R 0 

Q 2 

Q 0 

Q 

R 3 

P 

2 

0 

•In jedem 

Iterationsschritt 

Teilen der 

einzelnen 

Zwischenstrecken 

bei 1/4 bzw. 3/4 

k = 0 k = 1 k = 2 

k = 3 k = 4 

k = 5 


37 


38 

Unterteilungskurven 

• Weitere Unterteilungsalgorithmen für Kurven (und auch 

Flächen) werden im Wahlpflichtfach “CAAD und 

Geometrie” vorgestellt 

• Bsp: Interpolierender Unterteilungsalgorithmus 

GEOMETRIE 

0 1 2 

3 

4 

5 

5 


39

Splines

Sie wollen auch ein ePaper? Erhöhen Sie die Reichweite Ihrer Titel.

Template löschen?

Als Template speichern?