9. Schulst. (alle)

ab Ende der 9. Schulstufe 

5-EURO GEDENKMÜNZE 

5-Euro Gedenkmünzen in Silber werden in Österreich auf Basis eines regelmäßigen 

Neunecks ausgegeben. 

Beispiel aus dem Jahre 2009 (Quelle: 

Österreichische Nationalbank unter 

http://www.oenb.at/de/img/dl_euro- 

muenzen_in_oesterreich_- 

_ausgabe_2010_tcm14-190625.pdf - Seite 40) 

„200. Todestag Joseph Haydn“ 

Ausgabedatum: 14. Jänner 2009 

Auflage: 100.000 Handgehoben 

450.000 Normalprägung 

Durchmesser: 28,5 mm 

Feingewicht: 8g 

Legierung: 80,0 % Silber, 20,0 % Kupfer 

Ein regelmäßiges Neuneck kann aber nicht ausschließlich mit Zirkel und Lineal 

konstruiert werden. Für eine näherungsweise Konstruktion (ausschließlich mit Zirkel und 

Lineal) gibt es viele Methoden. In der Literatur findet man zum Beispiel folgende Idee: 

Der zur Konstruktion notwendige 

Zentriwinkel AMB wurde hier 

näherungsweise mit Hilfe eines 

rechtwinkeligen Dreiecks mit den 

Katheten AM 6 cm und AB 5 cm 

konstruiert. 

Wie groß ist der näherungsweise konstruierte Zentriwinkel AMB in dieser 

Näherungskonstruktion und um wie viel Prozent weicht der näherungsweise konstruierte 

Zentriwinkel AMB vom richtigen Zentriwinkel AMB ab? 

5-Euro Gedenkmünze 1

Möglicher Lösungsweg 

5 

tan( AMB) 

AMB 

39,805571 

6 

Exakter Zentriwinkel AMB 

360 

: 9 40 

Anteil AMB 

p 0,995139 Die Abweichung beträgt weniger als 0,5%. 

Grundwert 40 

Klassifikation 

Bezug zu Grundkompetenzen des sRP-Konzepts 

1. Algebra und Geometrie 

Trigonometrie 

Definitionen von sin, cos, tan im rechtwinkeligen Dreieck kennen und zur Auflösung 

rechtwinkeliger Dreiecke einsetzen können 

Wesentliche Bereiche der Handlungsdimension 

H2 

elementare Rechenoperationen in den jeweiligen Inhaltsbereichen planen und durchführen 

Wesentliche Bereiche der Inhaltsdimension 

I1 

Winkelmaße; sin α, cos α, tan α; Sinus- und Cosinussatz 

Wesentliche Bereiche der Komplexitätsdimension 

K2 

Herstellen von Verbindungen 

Kommentar 

In der Angabe sind nur wenige Informationen für die Lösung der Aufgabe notwendig. Die Schüler/innen 

müssen zuerst den Text nach notwendigen Informationen filtern. 

In der Beschreibung der Grundkompetenzen werden drei Aspekte in Zusammenhang mit Trigonometrie 

genannt. Für die näherungsweise Berechnung des Zentriwinkels ist ausschließlich die Grundkompetenz 

„Definitionen von sin, cos, tan im rechtwinkeligen Dreieck kennen und zur Auflösung 

rechtwinkeliger Dreiecke einsetzen können“ notwendig. Für die Berechnung des Prozentsatzes sind 

auch zurückliegende Kenntnisse aus der Prozentrechnung erforderlich (nachhaltiges Lernen). 

Diese Aufgabe erscheint daher als Unterrichtsaufgabe besonders gut geeignet. 

5-Euro Gedenkmünze 2

AUSSAGEN ÜBER LINEARE FUNKTIONEN 


Kreuze in der Tabelle an, welche Aussagen bezüglich linearer Funktionen der Form 

y k x d wahr bzw. falsch sind. 

A Jede lineare Funktion mit k 0 hat mit jeder Achse genau einen Punkt gemeinsam 

(schneidet genau einmal). 

B Jede lineare Funktion mit d 0 hat genau eine Nullstelle. 

C Jede lineare Funktion lässt sich als direktes Verhältnis interpretieren. 

D Jedes direkte Verhältnis lässt sich als lineare Funktion deuten. 

E Der Graph einer linearen Funktion ist stets eine Gerade. 

F Zu jeder Geraden im Koordinatensystem lässt sich eine lineare Funktion aufstellen. 

Begründe alle Fälle, bei denen du dich für falsch entschieden hast. 

Begründung 

A 

B 

C 

D 

E 

F 

wahr 

falsch 

wahr 

falsch 

wahr 

falsch 

wahr 

falsch 

wahr 

falsch 

wahr 

falsch 

keine Hilfsmittel erforderlich gewohnte Hilfsmittel möglich besondere Technologie erforderlich 

Aussagen über lineare Funktionen 1


Begründung 

A 

B 

C 

D 

E 

F 

wahr 

falsch 

wahr 

falsch 

wahr 

falsch 

wahr 

falsch 

wahr 

falsch 

wahr 

falsch 

Lineare Funktionen mit der Gleichung y d, d 0 haben keine 

Nullstelle, daher falsch. 

Bei einem direkten Verhältnis müsste d 0 sein, was nicht 

angenommen werden kann, daher falsch. 

Für Gerade, die parallel zur 2. Achse sind, lässt sich keine Funktion 

finden, weil einem x-Wert unendlich viele y-Werte zugeordnet sind. 




2. Funktionale Abhängigkeiten 

Lineare Funktion f(x) k x d 

Die Wirkung der Parameter k und d kennen und die Parameter in unterschiedlichen 

Kontexten deuten können 


H3 

mathematische Begriffe oder Sätze im jeweiligen Kontext deuten 


I2 charakteristische Eigenschaften von linearen und quadratischen Funktionen, 

Polynomfunktionen, von einfachen rationalen Funktionen, Winkelfunktionen, Potenz- und 

Wurzelfunktionen sowie Exponential- und Logarithmusfunktionen 


K3 

Einsetzen von Reflexionswissen, Reflektieren 

Kommentar 

Auf eine Begründung, warum eine Aussage richtig ist, wurde bewusst verzichtet. Nachdem es nur zwei 

Möglichkeiten gibt, reicht es zu begründen, warum eine Aussage falsch ist, was vermutlich einfacher ist. 

Die Aufgabe ist schon durch das vorgegebene Antwortformat besonders gut als Test- oder Diagnoseaufgabe 

geeignet. 


BAUSPAREN 


Herr Karl hat in Mathematanien – ein Land das sich durch besonders einfache Zahlen 

bei Rechnungen auszeichnet – einen Bausparvertrag beginnend mit 01.01.2010 

abgeschlossen. Er bezahlt an jedem Monatsbeginn 1000 € ein, die Verzinsung erfolgt 

vierteljährlich, d. h. am Ende der Monate März, Juni, September und Dezember mit 

einem sagenhaften Zinssatz von jeweils 10%, die Zinsen werden mit der Einzahlung am 

darauf folgenden Monatsersten gut geschrieben. 

a) Stelle eine Tabelle auf, die für jeden Monatsanfang des Jahres 2010 den 

Kontostand angibt. 

b) Stelle den Kontostand graphisch so dar, dass der Kontostand für jeden Tag des 

Jahres abgelesen werden kann. 

c) Wie wirkt sich die vierteljährliche (halbjährlich, ganzjährig, monatlich) Verzinsung 

am Graphen aus? 

d) Welche Darstellungsform findest du für diese Funktion geeignet? Begründe deine 

Aussage. 


a) 

Datum Einzahlung Kontostand 

01.01.2010 1000,00 1000,00 

01.02.2010 1000,00 2000,00 

01.03.2010 1000,00 3000,00 

01.04.2010 300,00 

01.04.2010 1000,00 4300,00 

01.05.2010 1000,00 5300,00 

01.06.2010 1000,00 6300,00 

01.07.2010 630,00 

01.07.2010 1000,00 7930,00 

01.08.2010 1000,00 8930,00 

01.09.2010 1000,00 9930,00 

01.09.2010 993,00 

01.10.2010 1000,00 11923,00 

01.11.2010 1000,00 12923,00 

01.12.2010 1000,00 13923,00 

01.01.2011 1392,30 15315,30 


Bausparen 1

) Graphisch: 

c) Der Sprung bei der Verzinsung ist größer als bei normalen Einzahlungen. 

Vierteljährlich: 3 Sprünge unterscheiden sich von den anderen 

Halbjährlich: nur ein Sprung ist größer 

Ganzjährig: alle Sprünge sind gleich groß 

Monatlich: die Sprünge werden immer größer 

d) Mögliche Erläuterungen: 

Der Kontostand kann aus der Tabelle am besten abgelesen werden, da muss 

auch nichts mehr berechnet werden im Gegensatz zur verbalen Beschreibung, die 

allerdings die Berechnung erklärt und so die Erstellung der Tabelle erst 

ermöglicht. Aus dem Graphen können keine genauen Werte abgelesen werden, er 

zeigt nur die ungefähre Entwicklung des Kontostandes. 

Bausparen 2




Funktionsbegriff, reelle Funktionen, Darstellungsformen und Eigenschaften 

Funktionen als mathematische Modelle verstehen und damit verständig arbeiten 

können 


a) H1 alltagssprachliche Formulierungen in die Sprache/Darstellung der Mathematik 

übersetzen 

b) H1 einen gegebenen mathematischen Sachverhalt in eine andere (tabellarische, 

grafische, symbolische, rekursive oder werkzeugspezifische) Darstellungsform 

übertragen; zwischen Darstellungen oder Darstellungsformen wechseln 

c) H3 tabellarisch, grafisch oder symbolisch gegebene Zusammenhänge erkennen, 

beschreiben und im jeweiligen Kontext deuten 

d) H1 einen gegebenen mathematischen Sachverhalt in eine andere (tabellarische, 




a) 

b) 

c) 

d) 

I2 

Funktionen: Begriff und Darstellungsformen (z.B. Text, Tabelle, Graph, Term, 

Gleichung, Parameterform, rekursive Darstellung) 


a) 

b) 

c) 

d) 

K1 

K3 

Einsetzen von Grundkenntnissen und Grundfertigkeiten 


Kommentar 

Die Zahlen wurden bewusst so gewählt, dass die Tabelle im Kopf gerechnet werden kann, und die 

Effekte in der graphischen Darstellung deutlich erkennbar werden (deshalb auch das fiktive Land 

Mathematien). 

Auf die Bedeutung der Endpunkte in der grafischen Darstellung ist einzugehen. 

ausgefüllt: der Punkt gehört zum Graphen 

nicht ausgefüllt: der Punkt gehört nicht zum Graphen 

Bausparen 3

BOOTSFAHRT 


Die Physik verwendet zur Beschreibung von Bewegungen für die Größen Weg, 

Geschwindigkeit und Beschleunigung Vektoren (gerichtete Größen). 

Damit können z.B. zwei Geschwindigkeiten, die gleichzeitig an einem Körper in 

verschiedene Richtungen wirken, vektoriell addiert werden. 

Ein Boot fährt mit einer Geschwindigkeit 

 

u10 

km/h 

 

u steht normal zur Strömungsgeschwindigkeit v des Flusses, wobei 

von einem Flussufer zum anderen. 

 

v 5 

km/h 

a) Bestimme graphisch die Richtung und den Betrag der tatsächlichen Geschwindigkeit 

w des Bootes sowie den Winkel, den sie mit der Normalen zur 

 

Strömungsrichtung einschließt. Kontrolliere deine Ergebnisse durch Rechnung. 

ist. 

b) Der Bootsmann möchte tatsächlich normal zur Strömungsrichtung fahren. Dazu 

muss er etwas gegen die Strömungsrichtung steuern. Unter welchem Winkel muss 

das Boot gegen die Strömung gesteuert werden, damit es den Fluss normal zur 

Strömungsrichtung überquert? Löse graphisch und durch eine Rechnung. 


Bootsfahrt 1


a) u ... Geschwindigkeitsvektor des Boots, v ... Geschwindigkeitsvektor der Strömung 

 

0 5 

5 

 

u v w, w , w 

125 5 5 11,18 

10 

0 

10 

 

 

v 

5 5 

( u,w) 

, sin( ) 

0,447 

 

26,6 

125 5 

w 

Das Boot fährt mit einer Geschwindigkeit von etwa 11,2 km/h in einem Winkel von 

ungefähr 26,6° zur geplanten Fahrtrichtung (normal zur Strömung). 

b) 

cos(α ) 

v 

 

w 

 

 

5 

10 

 

1 

0,5 

2 

 

α 60 

Das Boot muss in einem Winkel von 60° gegen die Strömung gesteuert werden, 

um den Fluss normal zur Strömungsrichtung zu überqueren. 

Bootsfahrt 2




Vektoren 

Vektoren geometrisch (als Punkte bzw. Pfeile) deuten und verständig einsetzen können 


H2 



I1 

Vektoren: Darstellungsformen, Operationen und Rechenregeln 


K3 


Kommentar 

Da Vektoren in vielen Gebieten der Physik gebraucht werden, sollen im Unterricht anwendungsorientierte 

physikalische Aufgaben nicht fehlen. Für Schulformen ohne Physik in der 5. Klasse sind 

gegebenenfalls zusätzliche Erläuterungen hilfreich. 

Das vektorielle Modell für Geschwindigkeit erlaubt die Bearbeitung komplexerer Bewegungsaufgaben. 

Entscheidend ist dabei das Prinzip, gleichzeitig ablaufende Bewegungsvorgänge im Modell hintereinander 

abzubilden. Damit kann diese Unterrichtsaufgabe zu einem Aufgabenpaket erweitert werden. 

Die Zusammensetzung von Kräften bzw. die Addition von Geschwindigkeiten nach dem Prinzip der 

Vektorrechnung gehört zu den Grundgesetzen der Mechanik und geht auf Isaac Newton zurück, der 

diese mathematischen Zusammenhänge richtig erkannte. Die Vektorrechnung selber wurde viel später 

entwickelt. 

Bootsfahrt 3

FIEBERMESSUNG 


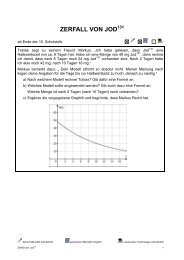
In einem Krankenhaus wird normalerweise immer um 6 Uhr früh und um 11 Uhr vormittags 

die Temperatur der Patienten/innen gemessen. Bei erhöhter Temperatur werden 

zusätzliche Werte um etwa 16 Uhr und 19 Uhr erhoben. Untenstehende Grafik zeigt die 

Temperaturwerte eines Patienten während der ersten 4 Tage. 

a) Wie sind die Verbindungslinien zwischen den Messpunkten zu interpretieren? 

b) Finde eine Begründung für diese Art der Messvorschrift. 

c) Wie interpretierst du die letzten zwei Messpunkte und die Verbindungslinie? 


a) Z.B.: Die Verbindungslinien geben eine Tendenz der Fieberkurve wieder, es 

können auf keinen Fall Zwischenwerte abgelesen werden. 

b) Z.B.: Hat ein/e Patient/in Fieber liegen die Messpunkte 11 Uhr und 6 Uhr zu weit 

auseinander, um den Verlauf einigermaßen genau wieder geben zu können. 

c) Z.B.: Die Messung um 11 Uhr ist ausgefallen, der Patient dürfte fieberfrei geblieben 

sein, Zwischenwerte können nicht abgelesen werden. 


Fiebermessung 1





Aus Tabellen, Graphen und Gleichungen von Funktionen Werte(paare) ermitteln und im 

Kontext deuten können 

Funktionen als mathematische Modelle verstehen und damit verständig arbeiten können 


H3 

Werte aus Tabellen oder grafischen Darstellungen ablesen, sie im jeweiligen Kontext 

deuten 


I2 

Funktionen: Begriff und Darstellungsformen (z.B. Text, Tabelle, Graph, Term, Gleichung, 

Parameterform, rekursive Darstellung) 


K1 


Kommentar 

Das Bespiel ist eher als Diagnosebeispiel gedacht. 

Die Interpretationen der Schüler/innen zeigen, wie sie Graphen interpretieren, ob sie ein Grundverständnis 

haben oder den Graphen falsch deuten. Ganz persönliche Antworten sind erwünscht. 

Durch die Fragestellung soll keine Richtung vorgegeben werden, wie Schüler/innen zu denken haben. 

Die Angabe erfolgte nach Rücksprache mit einer Krankenschwester; bei Bedarf können noch 

zusätzliche Messpunkte dazu kommen. 

Fiebermessung 2

FLÄCHENFUNKTION 


Gegeben ist das Dreieck ABC, dessen Maße der Zeichnung zu entnehmen sind. 

Bewegt man den Punkt D auf der Verbindungsgeraden zwischen A und C, so wird in 

Abhängigkeit von der Strecke x eine Fläche mit dem Flächeninhalt F(x) erzeugt. 

a) Stelle den Zusammenhang zwischen der Länge der Strecke x und dem Flächeninhalt 

F(x) der entstehenden Flächen in der nachfolgenden Tabelle dar. 

x 

F(x) 

b) Stelle diesen Zusammenhang in dem oben angegebenen Diagramm dar. Beachte 

dabei den Maßstab auf der 2. Achse. 

c) Stelle die Funktionsgleichung für F(x) auf. 


Flächenfunktion 1


a) 

x 0 1 2 3 4 5 6 7 8 

F(x) 0,00 0,25 1,00 2,25 4,00 6,25 9,00 12,25 16,00 

b) 

c) Die Funktionsgleichung lautet 

y 

x 

4 

2 

Flächenfunktion 2





Zwischen tabellarischen und grafischen Darstellungen funktionaler Zusammenhänge 

wechseln können Aus Tabellen, Graphen und Gleichungen von Funktionen Werte(paare) 

ermitteln und im Kontext deuten können 


H1 

einen gegebenen mathematischen Sachverhalt in eine andere (tabellarische, grafische, 

symbolische, rekursive oder werkzeugspezifische) Darstellungsform übertragen; zwischen 

Darstellungen oder Darstellungsformen wechseln 


I2 




K2 


Kommentar 

Die Aufgabe ist als Unterrichtsaufgabe gedacht, bei der eine Vernetzung der Grundkompetenzen aus 

den Inhaltsbereichen Geometrie und funktionale Abhängigkeiten erfolgt. 

Verschiedene Lösungswege für die Bestimmung des Flächeninhalts und damit auch für das Finden der 

Funktionsgleichung sind möglich, z.B. Ablesen der Längen der Katheten aus der Graphik oder 

Anwenden des Strahlensatzes. Damit eignet sich die Aufgabe sogar schon ab der 8. Schulstufe. 

Die Aufgabe umfasst den einfachen Wechsel der Darstellungsform von der Tabelle zum Graphen. 

Anspruchsvoller ist der Wechsel zur Funktionsgleichung. 

Flächenfunktion 3

FÜLLKURVEN 


Die dargestellten Rotationskörper werden über einen Zufluss, der eine konstante 

Wassermenge pro Zeiteinheit garantiert, gefüllt. Dabei wird die Höhe des Wasserstandes 

abhängig von der Zeiteinheit gemessen und aufgezeichnet. Der entstehende 

Graph wird Füllkurve genannt. 

Ordne den Füllkurven durch Ankreuzen der richtigen Ziffern den zugehörigen Körper zu. 

1 

1 

2 

3 

4 

1 

2 

2 

3 

4 

1 

3 

2 

3 

4 

1 

4 

2 

3 

4 


Füllkurven 1


1 

1 

2 

3 

4 

1 

2 

2 

3 

4 

1 

3 

2 

3 

4 

1 

4 

2 

3 

4 

Füllkurven 2







H3 

tabellarisch, grafisch oder symbolisch gegebene Zusammenhänge erkennen, beschreiben 

und im jeweiligen Kontext deuten 


I2 




K3 


Kommentar 

Bei dieser Aufgabe sollen die Schüler/innen intuitiv eine funktionale Abhängigkeit erfassen. Ausgehend 

von der räumlichen Vorstellung soll der Einfluss der Querschnittsfläche auf die Höhenveränderung in 

Abhängigkeit von der Zeit erkannt werden. 

Die Aufgabe ist sehr gut für kooperative Lernformen wie Gruppen- und Partnerarbeit geeignet 

(Kompetenzentwicklung durch „Reden über ...“). 

Füllkurven 3

FUNKTIONSGRAPH – JA ODER NEIN 


Sind die folgenden Darstellungen Graphen von reellen Funktionen 

Kreuze an und begründe die Antwort. 

f : x f(x) ? 

Ja 

Begründung: 

Nein 

Ja 

Nein 

Begründung: 

Ja 

Nein 

Begründung: 

Ja 

Begründung: 

Nein 


Funktionsgraph – JA oder NEIN 1


Ja 

Nein 

Begründung: 

Zu jedem x-Wert gibt einen 

eindeutigen Funktionswert. 

Ja 

Nein 

Begründung: 

Zu den x-Werten (ausgenommen 

x=4) gibt jeweils 2 Funktionswerte. 

Ja 

Nein 

Begründung: 

Zum x-Wert 2 existieren unendlich 

viele unterschiedliche Funktionswerte. 

Ja 

Nein 

Begründung: 

Zu jedem x-Wert existiert ein 

eindeutiger Funktionswert. 






Für gegebene Zusammenhänge entscheiden können, ob man sie als Funktionen 

betrachten kann 


H4 

die Entscheidung für eine mathematische Handlung oder eine mathematische Sichtweise 

problembezogen argumentativ belegen 


I2 




K1 


Kommentar 

Bei dieser Aufgabe wird eine Wiederholung und Vertiefung des Funktionsbegriffes angestrebt. Die 

Entscheidungen sollen argumentativ begründet werden. Grundkenntnisse können erweitert werden. 

Partner- oder Gruppenarbeit erscheint geeignet, besonderes Augenmerk kommt dabei der Präsentation 

zu. Auf die Verwendung der korrekten Fachsprache soll geachtet werden. 


GLEICHUNG IN 2 VARIABLEN - LINEARE 

FUNKTION 


Unter welchen in der nachstehenden Tabelle angegebenen Bedingungen entspricht eine 

Gleichung a x b y c, (a,b,c R) 

einer linearen Funktion mit y f(x) ? 

Kreuze in der Tabelle an und begründe deine Entscheidung. 

Falls es sich um eine Funktion handelt, gib die zugehörige Funktionsgleichung in der 

Form y k x d an und skizziere, wie der Graph aussehen könnte. 

Lineare 

Funktion 

Funktionsgleichung 

Graph 

Begründung 

a 0 

b, c 0 

ja 

nein 

b 0 

a, c 0 

ja 

nein 

c 0 

a, b 0 

ja 

nein 

a 0 

c 0 

b 0 

ja 

nein 


Gleichung in 2 Variablen - lineare Funktion 1


Lineare 

Funktion 

Funktionsgleichung 

Graph 

Begründung 

a 0 

b, c 0 

ja 

nein 

y 

c 

b 

Gerade muss parallel 

zur 1. Achse sein. 

Steigung: k 0 

oder 

b 0 

a, c 0 

ja 

nein 

Einem x-Wert werden 

unendlich viele 

y-Werte zugeordnet. 

c 0 

a, b 0 

ja 

nein 

y 

 

a 

b 

x 

Homogene lineare 

Funktion, die durch 

den Ursprung geht. 

d 0 

oder 

a 0 

c 0 

b 0 

ja 

nein 

y 0 

Die Gerade liegt auf 

der x-Achse. 






Formeln als Darstellung von Funktionen interpretieren und den Funktionstyp zuordnen 

können 


H1 

H4 

problemrelevante mathematische Zusammenhänge identifizieren und mathematisch 

darstellen 

mathematische Argumente nennen, die für oder gegen die Verwendung eines bestimmten 

mathematischen Begriffs, eines Modells, einer Darstellung oder eines bestimmten 

Lösungswegs bzw. für oder gegen eine bestimmte Lösung oder Interpretation sprechen 


I2 




K3 


Kommentar 

Die Aufgabe stellt eine Verbindung zwischen Algebra und Funktionenlehre her und ist nicht nur ein 

Beitrag zur Förderung von vernetztem Denken sondern auch ein wichtiger Baustein bei der Lösung 

komplexerer Aufgaben (Bauaufgaben). 

Die Aufgabe ist für den Unterricht und als Test- oder Diagnoseaufgabe geeignet. 

Als Arbeitsweise wären auch Partner- oder Gruppenarbeit empfehlenswert. 


GLEICHUNGEN - GRAVITATION 


Der Wikipedia-Artikel über Gravitation enthält folgenden Absatz: 

Gemäß der newtonschen Gravitationstheorie erzeugt jede (schwere) Masse ein Gravitationsfeld, in 

der allgemeinen Relativitätstheorie aber auch jede andere Energieform, also neben schweren 

Massen auch Licht- und Gravitationsenergie. 

Die Stärke der Gravitationsbeschleunigung g in einem durch schwere Massen erzeugten 

Gravitationsfeld ist dabei zum einen der Größe der Masse M proportional, zum anderen dem 

Quadrat des Abstandes r zum Mittelpunkt von M umgekehrt proportional. Für g gilt damit die 

Definitionsgleichung 

M 

g G , 

2 

r 

in der G die newtonsche Gravitationskonstante ist, eine Naturkonstante, deren Wert man, sofern 

die Werte der übrigen Größen durch Messung bekannt sind, durch Umformen obiger Gleichung 

nach G bestimmen kann. 

http://de.wikipedia.org/wiki/Gravitation (06.07.2010) 

Um wie viel stärker oder schwächer ist die Gravitationsbeschleunigung g für einen 

Körper mit doppelter Masse und halbem Abstand? 

g 

neu 

2 M 

G 

2 

r 

 

2 


2 M 

4 2 M 

M 

G G 8 G 8 g 

2 

2 

2 

r r 

r 

4 

Die Gravitationsbeschleunigung wächst auf das Achtfache. 

alt 

 


Gleichungen - Gravitation 1




(Un)gleichungen und Gleichungssysteme 

Lineare Gleichungen aufstellen, interpretieren, umformen/lösen und die Lösung im Kontext 

deuten können 


H2 







K3 


Kommentar 

Im Sinne einer Entwicklung von Kommunikationsfähigkeit erscheint die Arbeit mit authentischen Texten 

von zunehmender Bedeutung. Darüber hinaus geht es um eine Transfer-Leistung: vorhandene 

Kompetenzen sollen auch auf neue (Anwendungs-)Situationen übertragen werden können. 

Gleichungen - Gravitation 2

GLEICHUNGEN - HEFTE 


Im Archiv einer Schule werden alle Mathematik-Schularbeitshefte einer bestimmten 

Klasse aufbewahrt. Jede Schülerin/jeder Schüler hat genau ein Heft abgegeben; die 

Hefte haben entweder 20 Blatt oder 40 Blatt. 

Es sei z die Anzahl der Hefte mit 20 Blatt und v Anzahl der Hefte mit 40 Blatt. 

z v 25 

Es gelten zwei Bedingungen: 

20z 40v 660 

a) Wie viele Schülerinnen und Schüler besuchen die erwähnte Klasse? 

b) Wie viele Blatt Papier haben alle Mathematik-Schularbeitshefte dieser Klasse 

zusammen? 

c) Erweiterung 

Ein Schüler möchte die oben gestellte Aufgabe lösen. Er macht jedoch einen 

Angabefehler und schreibt in sein Heft die folgenden Bedingungen: 

z v 25 

20z 40v 650 

Macht dieser Angabefehler für die Beantwortung der Fragen a) und b) einen 

wesentlichen Unterschied? 


a) 25 Schülerinnen und Schüler besuchen die erwähnte Klasse 

b) Alle Mathematik-Schularbeitshefte dieser Klasse haben zusammen 660 Blatt 

Papier 

c) Erweiterung 

Es scheint zunächst, dass die Antworten 25 und 650 nach demselben Schema 

gefunden werden können wie oben. 

Man kann aber nur sagen: Wenn es Lösungen gibt, dann lauten sie 25 und 650. 

Berechnet man mit einer geeigneten Methode die Anzahlen der beiden Heftsorten, 

so erhält man im ersten Fall die Werte z = 17 und v = 8, im zweiten Fall, aufgrund 

des „Angabefehlers“ jedoch die Werte z = 17,5 und v = 7,5. Für eine vernünftige 

Lösung kommen halbe Hefte nicht in Frage, daher besitzt das geänderte 

Problem keine Lösung. 

Eine entsprechende Überlegung ist auch allgemein möglich, ohne die Werte von z 

und v tatsächlich zu bestimmen. 


Gleichungen-Hefte 1




(Un)gleichungen und Gleichungssysteme 

Lineare Gleichungen aufstellen, interpretieren, umformen/lösen und die Lösung im 



a) 

b) 

c) 

H3 Zusammenhänge und Strukturen in Termen, Gleichungen (Formeln) und 

Ungleichungen erkennen, sie im Kontext deuten 


a) 

b) 

c) 

I1 

Variable, Terme, Gleichungen, Ungleichungen und Gleichungssysteme 


a) K1 Einsetzen von Grundkenntnissen und Grundfertigkeiten 

b) 

b) K3 Einsetzen von Reflexionswissen, Reflektieren 

Kommentar 

Die Aufgabe zielt zunächst auf den in der Beschreibung der sRP-Grundkompetenzen genannten 

Aspekt „Gleichungssysteme im Kontext interpretieren können“. 

Die Fragen verlangen nicht die Ermittlung der Unbekannten, die Botschaft scheint klar: Wer rechnet, ist 

selber schuld. 

Die Erweiterung relativiert jedoch diese Erkenntnis, indem sie ein Nachdenken über die Existenz von 

Lösungen erfordert. Vermutlich wird dabei auch eine operative Tätigkeit erfolgen (die Ermittlung der 

Unbekannten), jedoch steht diese nicht im Zentrum der Aufgabenstellung. 

Keine der Teilaufgaben a), b) und c) geht über Grundkompetenzen hinaus. 

Die Kennzeichnung von c) als „Erweiterung“ erfolgt hier aus taktischen Gründen und betont den 

Wechsel der Komplexitätsanforderung. 

Gleichungen-Hefte 2

GRAPH EINER LINEAREN FUNKTION 


a) Zeichne den Graphen einer linearen Funktion mit einer negativen ganzzahligen 

Steigung in das vorgegebene Koordinatensystem. 

b) Wie lautet der Funktionsterm des von dir gezeichneten Graphen? 

keine Hilfsmittel erlaubt gewohnte Hilfsmittel möglich besondere Technologie erforderlich 

Graph einer linearen Funktion 1


a) 

b) f(x) x 

2 






 




a) H1 alltagssprachliche Formulierungen in die Sprache/Darstellung der Mathematik 

übersetzen 

b) H1 einen gegebenen mathematischen Sachverhalt in eine andere (tabellarische, 




a) 

b) 

I2 




a) 

b) 

K1 


Kommentar 

Wiederholungsaufgabe aus der Sekundarstufe 1 

Die Funktionsgleichung einer Geraden soll aus der graphischen Darstellung ermittelt werden. 



GRAPHEN LINEARER FUNKTIONEN ERKENNEN 


Welche der fünf Abbildungen stellen nicht Graphen einer linearen Funktion dar? 

Begründe deine Meinung 

Abb. 1 Abb. 2 Abb. 3 

Abb. 4 Abb. 5 


Die Abbildung 2 stellt keinen Graphen einer Funktion dar, weil einem x-Wert unendlich 

viele y-Werte zugeordnet sind. 

Die Abbildung 4 stellt keinen Graph einer linearen Funktion dar, weil die Steigung nicht 

gleich bleibt. 


Graphen linearer Funktionen erkennen 1





Verbal, tabellarisch, grafisch oder durch eine Gleichung (Formel) gegebene lineare 

Zusammenhänge als lineare Funktionen erkennen bzw. betrachten können; zwischen 

diesen Darstellungsformen wechseln können 


H3 








K3 


Kommentar 

Die Aufgabe erfordert ein Nachdenken über den Begriff „Funktion“ im Allgemeinen und den Begriff 

„lineare Funktion“ im Besonderen. Das Verständnis der Definition „lineare Funktion“ ist Voraussetzung 

für die geforderte verbale Begründung. 


Graphen linearer Funktionen erkennen 2

GRAPHEN ZUORDNEN 


Gegeben sind die Funktionen f 1 , f 2 , f 3 und f 4 . 

Ordne den gegebenen Graphen 

den jeweils entsprechenden 

Funktionsterm und alle zutreffenden 

Eigenschaften zu. 

Kreuze deine Ergebnisse in 

der Tabelle an. 

f 1 f 2 f 3 f 4 

a 

g 1 

(x) , a > 0 

x 

 

a 

g 2 

(x) , a < 0 

x 

 

a 

g3(x) 

 

2 

x 

, a > 0 

a 

x 

g4(x) 

, a < 0 

2 

 

Der Graph ist symmetrisch bezüglich der y-Achse. 

Der Graph ist symmetrisch zum Nullpunkt. 

Es gilt: f(-x) = -f(x). 

Es gilt: f(x) = f(-x). 

Für x > 0 ist f(x) > 0. 

Für x > 0 ist f(x) < 0. 

Für x < 0 ist f(x) > 0. 


Graphen zuordnen 1


f 1 f 2 f 3 f 4 

a 

g 1 

(x) , a > 0 

x 

 

a 

g 2 

(x) , a < 0 

x 

 

a 

g3(x) 

 

2 

x 

, a > 0 

a 

x 

g4(x) 

, a < 0 

2 

 

Der Graph ist symmetrisch bezüglich der y-Achse. 

Der Graph ist symmetrisch zum Nullpunkt. 

Es gilt: f(-x) = -f(x). 

Es gilt: f(x) = f(-x). 

Für x > 0 ist f(x) > 0. 

Für x > 0 ist f(x) < 0. 

Für x < 0 ist f(x) > 0. 

Graphen zuordnen 2





Eigenschaften von Funktionen erkennen, benennen, im Kontext deuten und zum Erstellen 

von Funktionsgraphen einsetzen können: Monotonie, Monotoniewechsel (lokale Extrema), 

Wendepunkte, Periodizität, Achsensymmetrie, asymptotisches Verhalten, Schnittpunkte 

mit den Achsen 

Potenzfunktion mit 

z 

2 

f(x) a x b, z Z sowie f(x) a x b 

Die Wirkung der Parameter a und b kennen und die Parameter im Kontext deuten können 

1 


H3 

zutreffende und unzutreffende Interpretationen erkennen 






K1 


Kommentar 

Das Kennen und Erkennen wesentlicher Eigenschaften von Potenzfunktionen wie Monotonie und 

Symmetrie sind eine wichtige Grundkompetenz für weiterführende Problemlöseaufgaben. 

Werden mit Hilfe dieser Aufgabe neue Inhalte erarbeitet, können die Graphen den Funktionstermen 

durch Einsetzen geeigneter Zahlenwerte zugeordnet werden; im Falle einer Wiederholung sollten die 

typischen Verläufe der Graphen schon bekannt sein. 

Die Begriffe „Symmetrie“ und „gerade“ bzw. „ungerade Funktion“ sollten in jedem Fall bereits geläufig 

sein. 

Die vorliegende Aufgabe ist als Unterrichtsbeispiel (z. B. in Form einer Partnerarbeit) aber auch als 

Diagnoseinstrument vorstellbar. 

Graphen zuordnen 3

KRÄFTE 


Drei an einem Punkt P eines Körpers angreifende Kräfte F, 1 

F 

2 

und F 3 

lassen sich durch 

eine einzige am selben Punkt angreifende resultierende Kraft F ersetzen, die allein 

dieselbe Wirkung ausübt wie F, 1 

F 

2 

und F 3 

zusammen. Die Kraft F kann man mittels 

Kräfteparallelogrammen konstruieren. 

a) Gegeben sind drei an einem Punkt P angreifende Kräfte F, 1 

F 

2 

und F 3 

. 

Ermittle grafisch die resultierende Kraft F als Summe der Kräfte F, 1 

F 

2 

und F 3 

. 

b) Gegeben sind drei an einem Punkt P angreifende Kräfte F, 1 

F 

2 

und F 3 

. 

Ermittle grafisch die resultierende Kraft F als Summe der Kräfte 1 

F, 2 

F und 3 

F . 

Interpretiere das Ergebnis. 


Kräfte 1


a) 

b) 

Interpretation: Der Betrag der resultierenden Kraft F ist null, die drei Kräfte 

befinden sich im Gleichgewicht. 

Kräfte 2




Vektoren 

Vektoren geometrisch (als Punkte bzw. Pfeile) deuten und verständig einsetzen 

können 


a) H2 geometrische Konstruktionen durchführen 

b) H2 

H3 

geometrische Konstruktionen durchführen 

Rechenergebnisse im jeweiligen Kontext deuten 


a) 

b) 

I1 




b) K2 Herstellen von Verbindungen 

Kommentar 







entwickelt. 

Kräfte 3

KRÄFTEPARALLELOGRAMM 


Zwei an einem Punkt P eines Körpers angreifende Kräfte F 1 

und F 2 

lassen sich durch 

eine einzige am selben Punkt angreifende resultierende Kraft F ersetzen, die allein 

dieselbe Wirkung ausübt wie F 1 

und F 2 

zusammen. Die Kraft F kann man mittels eines 

Kräfteparallelogramms konstruieren. 

Gegeben sind zwei an einem Punkt P angreifende Kräfte F 1 

und F. 

2 

Ermittle grafisch die resultierende Kraft F als Summe der Kräfte F 1 

und F. 

2 



Kräfteparallelogramm 1




Vektoren 



H2 

geometrische Konstruktionen durchführen 


I1 



K1 


Kommentar 







entwickelt. 

Kräfteparallelogramm 2

LAGEBEZIEHUNG VON GERADEN 1 


Entnimm die Lagebeziehungen der durch die Strecken AB, CD, EF und GH bestimmten 

Geraden aus der Zeichnung. 

Kreuze in der Tabelle die richtige Lagebeziehung an. 

g AB und g CD g AB und g EF g AB und g GH 

identisch 

schneidend 

parallel, 

aber nicht 

identisch 

identisch 

schneidend 


aber nicht 

identisch 

identisch 

schneidend 


aber nicht 

identisch 

g CD und g EF g CD und g GH g EF und g GH 

identisch 

schneidend 


aber nicht 

identisch 

identisch 

schneidend 


aber nicht 

identisch 

identisch 

schneidend 


aber nicht 

identisch 

Lagebeziehung von Geraden 1 1



identisch 

schneidend 


aber nicht 

identisch 

identisch 

schneidend 


aber nicht 

identisch 

identisch 

schneidend 


aber nicht 

identisch 


identisch 

schneidend 


aber nicht 

identisch 

identisch 

schneidend 


aber nicht 

identisch 

identisch 

schneidend 


aber nicht 

identisch 




Vektoren 

Geraden durch (Parameter-)Gleichungen in R 2 und R 3 angeben können; Geradengleichungen 

interpretieren können; Lagebeziehungen (zwischen Geraden und zwischen 

Punkt und Gerade) analysieren, Schnittpunkte ermitteln können 


H3 


deuten 


I1 

Geraden im R² und R³; Ebenen 


K1 


Kommentar 

Verschiedene Lösungsmöglichkeiten (Ermitteln der Steigung aus dem Steigungsdreieck, graphische 

Lösungsmöglichkeit) können besprochen werden. 

Welche Aussage über grafische Lösungen kann getroffen werden? Die Frage der mangelnden 

Exaktheit kann mit den Schülerinnen und Schülern diskutiert werden. 

Diese Aufgabe ist für den Einsatz im Unterricht gedacht, z.B. zum Wiederholen und Festigen der 

Begriffe Steigung und Steigungsdreieck. 




Entnimm die Lagebeziehungen der durch die Strecken AB, CD, EF und GH bestimmten 

Geraden aus der Zeichnung. 

Kreuze in der Tabelle die richtige Lagebeziehung an. 

Begründe deine Überlegungen. 


identisch 

schneidend 


aber nicht 

identisch 

identisch 

schneidend 


aber nicht 

identisch 

identisch 

schneidend 


aber nicht 

identisch 


identisch 

schneidend 


aber nicht 

identisch 

identisch 

schneidend 


aber nicht 

identisch 

identisch 

schneidend 


aber nicht 

identisch 





identisch 

schneidend 


aber nicht 

identisch 

identisch 

schneidend 


aber nicht 

identisch 

identisch 

schneidend 


aber nicht 

identisch 


identisch 

schneidend 


aber nicht 

identisch 

identisch 

schneidend 


aber nicht 

identisch 

identisch 

schneidend 


aber nicht 

identisch 

Mithilfe des vorgegebenen Rasters kann man die Steigung der Geraden bestimmen: 

 

3 1 

4 

1 

2,5 

g AB : k AB 

0, 5 g CD : k CD 

0, 4 g EF : k EF 

0, 5 g GH : k GH 

0, 5 

6 2 

9 

2 

5 

Die Geraden g AB , g EF und g GH haben die gleiche Steigung. Sie sind also parallel oder 

identisch. Mithilfe des Rasters erkennt man, dass die Geraden g AB und g EF identisch 

sind und die Gerade g GH parallel dazu liegt. 

Die Gerade g CD hat eine andere Steigung. Sie muss daher die drei Geraden g AB , g EF 

und g GH schneiden. 





Vektoren 





H3 

H4 


deuten 




I1 



K1 


Kommentar 

Verschiedene Lösungsmöglichkeiten (Ermitteln der Steigung aus dem Steigungsdreieck, graphische 

Lösungsmöglichkeit) können besprochen werden. 

Welche Aussage über grafische Lösungen kann getroffen werden? Die Frage der mangelnden 

Exaktheit kann mit den Schülerinnen und Schülern diskutiert werden. 

Diese Aufgabe ist für den Einsatz im Unterricht gedacht, z.B. zum Wiederholen und Festigen der 

Begriffe Steigung und Steigungsdreieck, kann aber auch als Diagnoseinstrument verwendet werden. 

Der Unterschied zur Aufgabe „Lagebeziehungen von Geraden 1“ besteht darin, dass die Schüler/innen 

ihre Vorgangsweise begründen müssen. Der Handlungsbereich H4 (Argumentieren und Begründen) 

wird zusätzlich angesprochen. 




Kreuze alle richtigen Aussagen an und begründe sie. 

a) 

b) 

c) 

d) 

Die Geraden Aussagen Begründung 

 

2 

3 sind parallel, aber nicht 

g : X s 

1 

4 

identisch. 

sind identisch. 

und 

schneiden einander und 

stehen aufeinander nicht 

4 

3 

h : X t normal. 

2 

4 

 


stehen aufeinander normal. 

 

2 

3 

g : X s 

1 

4 

 

und 

 

1 

1,5 

h : X t 

5 

2 

 

 

2 

3 

g : X s 

1 

4 

 

und 

 

1 

6 

h : X t 

2 

8 

 

 

2 

3 

g : X s 

1 

4 

 

und 

 

4 

2 

h : X t 

2 

1,5 

 

sind parallel, aber nicht 

identisch. 




normal. 




identisch. 




normal. 




identisch. 




normal. 






a) 

b) 

c) 

d) 

Die Geraden Aussagen Begründung 

 

2 

3 sind parallel, aber nicht Die Richtungsvektoren sind 

g : X s 

1 

4 

identisch. 

gleich und P(2|1) h: 


2 

und 


2 4 3t t 

3 


4 

3 

3 


1 2 

4t t 

2 

4 

4 

 


Da der Parameter t verschiedene 


Werte für die Koordinaten x und 

y annimmt, sind die Geraden 

nicht identisch. 

 

2 

3 sind parallel, aber nicht Die Richtungsvektoren sind 

g : X s 

1 

4 

identisch. 

3 

1,5 

 


parallel: 2 

und 

und 


4 

2 

stehen aufeinander nicht Q(1|5) g: 

1 

1,5 


1 2 3s s 1 

5 

2 

 

schneiden einander und 5 1 

4s s 1 


Da der Parameter s den gleichen 

Wert für die Koordinaten x und y 

annimmt, sind die Geraden 

identisch. 

 

2 

3 sind parallel, aber nicht Die Richtungsvektoren sind nicht 

g : X s 

1 

4 

identisch. 

parallel, da der eine Vektor kein 


Vielfaches des anderen Vektors 

und 

schneiden einander und ist. 

stehen aufeinander nicht Da das skalare Produkt 

1 

6 


3 

6 

2 

8 

 

schneiden einander und 

14 0 ist, stehen die 

4 8 


 

Vektoren nicht aufeinander 

normal. 

 

2 

3 sind parallel, aber nicht Die Richtungsvektoren stehen 

g : X s 

1 

4 

identisch. 

aufeinander normal: 


2 3 

und 

schneiden einander und 6 

6 0 


1,5 

4 

4 

2 


2 

1,5 

 







Vektoren 




Normalvektoren in R 2 aufstellen, verständig einsetzen und interpretieren können 


H3 

H4 

Zusammenhänge und Strukturen in Termen, Gleichungen (Formeln) und Ungleichungen 

erkennen, sie im Kontext deuten 





I1 



K2 


Kommentar 

Die Aufgabe kann im Unterricht eingesetzt werden um mit den Schülerinnen und Schülern 

verschiedene Lösungsmöglichkeiten der Aufgabenstellungen zu erläutern z.B.: 

- Ist auch eine grafische Lösung möglich? 

- Würden andere Darstellungsformen der Geraden die Beantwortung der Fragen erleichtern? 

Die Aufgabe eignet sich zum Wiederholen und Festigen des erworbenen Wissens. Die Aufgabenteile a) 

bis d) können aber auch einzeln als Testaufgaben Verwendung finden. 




Zwei Geraden im R 2 sind entweder schneidend, parallel oder identisch. 

5 

3 

Gegeben sind die Gerade g : X t und der Punkt P(-6|4) g. 

2 

4 

a) Gib eine Gleichung der Geraden h 1 durch P an, die zu g parallel ist. 

b) Gib eine Gleichung einer Geraden h 2 durch P an, welche die Gerade g schneidet. 

c) Gib eine Gleichung einer Geraden h 3 durch P an, die mit g identisch ist. 

d) Gib eine Gleichung der Geraden h 4 durch P an, die normal auf g steht. 

Berechne die Koordinaten des Schnittpunktes S. 


6 

3 

3 

a) z.B. h 1 

: X s Auch jeder zu parallele Vektor ist möglich. 

4 4 

4 

6 

1 

3 

b) z.B. h 2 

: X s Auch jeder zu nicht parallele Vektor ist möglich. 

4 4 

4 

c) Dieser Fall ist für diese Angabe nicht möglich, da der gegebene Punkt P(-3|8) 

nicht auf der Geraden g liegt. 

6 

4 

4 

d) z.B. h 4 

: X s Auch jeder zu parallele Vektor ist möglich. 

4 

3 

3 

Berechnung des Schnittpunkts: 

5 

3 

6 

4 

t s 

2 

4 

4 

3 

5 3t 6 

4s 

 

2 4t 4 3s 

50 25s 0 

s 2 

6 

4 2 

S 2 

 

4 

3 

 

2 

Schnittpunkt S(2|2) 






Vektoren 


interpretieren können; Lagebeziehungen (zwischen Geraden und 

zwischen Punkt und Gerade) analysieren, Schnittpunkte ermitteln können 


a) H1 problemrelevante mathematische Zusammenhänge identifizieren und mathematisch 

darstellen 

b) H1 

H2 


darstellen 

elementare Rechenoperationen in den jeweiligen Inhaltsbereichen planen und 

durchführen 

c) 

d) 

H1 problemrelevante mathematische Zusammenhänge identifizieren und mathematisch 

darstellen 


a) 

b) 

c) 

d) 

I1 



a) 

b) 

c) 

d) 

K1 


Kommentar 

Diese Aufgabe ist für den Einsatz im Unterricht gedacht. 

Die Teilaufgabe c) wurde bewusst so gewählt, um mit den Schülerinnen und Schülern über die 

Lösbarkeit der Fragstellung diskutieren zu können. 

Falls der gegebene Punkt auf der gegebenen Geraden liegt, ist Fall a) nicht möglich, dafür aber Fall c). 


LINEARE FUNKTIONEN MIT GLEICHEM d 


a) Zeichne drei verschiedene Graphen, die durch einen Funktionsterm der Form 

f(x) k x 2 dargestellt werden. 

b) Welche Wirkung hat eine Änderung des Parameters k auf den Graphen der 

Funktion? 

a) 


b) Eine Änderung von k bewirkt eine Drehung der Geraden um den Punkt (0|2) 

(allgemein (0|d)). 

oder: Eine Änderung von k bewirkt eine Änderung der Steigung. 


Lineare funktionen mit gleichem d 1





 




a) H1 einen gegebenen mathematischen Sachverhalt in eine andere (tabellarische, 



b) H3 tabellarisch, grafisch oder symbolisch gegebene Zusammenhänge erkennen, 



a) I2 Funktionen: Begriff und Darstellungsformen (z.B. Text, Tabelle, Graph, Term, 


b) I2 Einfluss von Parametern 


a) 

b) 

K1 


Kommentar 


Die Größe von k als Maß für die Steigung soll klar sein. Die Aufgabe ist für den Unterricht und als Testoder 

Diagnoseaufgabe geeignet. 

Lineare funktionen mit gleichem d 2

LINEARE FUNKTIONEN MIT GLEICHEM k 


a) Zeichne drei verschiedene Graphen, die durch einen Funktionsterm der Form 

f(x) = 2x + d dargestellt werden. 

b) Welche Wirkung hat eine Änderung des Parameters d auf den Graphen der 

Funktion? 

a) 


b) Eine Änderung von d bedeutet ein Parallelverschieben des Graphen durch den Punkt 

(0d). 

oder: Eine Änderung von d bewirkt einen anderen Abschnitt auf der 2. Achse. 


Lineare Funktionen mit gleichem k 1





 




a) H1 einen gegebenen mathematischen Sachverhalt in eine andere (tabellarische, 



b) H3 tabellarisch, grafisch oder symbolisch gegebene Zusammenhänge erkennen, 



a) I2 Funktionen: Begriff und Darstellungsformen (z.B. Text, Tabelle, Graph, Term, 


b) I2 Einfluss von Parametern 


a) 

b) 

K1 


Kommentar 


Im Hinblick auf den Aufbau nachhaltiger Kompetenzen ist die Bedeutung des Parameters d als ein 

Verschieben in Richtung der 2. Achse hier für lineare Funktionsgraphen und später für alle Funktionsgraphen 

zu erarbeiten. Die Aufgabe ist für den Unterricht und als Test- oder Diagnoseaufgabe geeignet. 

Lineare Funktionen mit gleichem k 2

PARALLEL ODER NORMAL 1 


 

1 

Gegeben ist der Vektor a . 

 

4 

Entscheide, ob die in der Tabelle angegebenen Vektoren zum Vektor a parallel, normal 

bzw. weder parallel noch normal sind und kreuze die richtigen Antworten an. 

parallel 

normal 

weder parallel 

noch normal 

 

1 

b 

 

4 

 

2 

c 

 

8 

 

4 

d 

1 

 

 

4 

e 

1 

 

1 

f 

4 

Parallel oder normal 1 1



normal 

weder parallel 

noch normal 

 

1 

b 

 

4 

 

2 

c 

 

8 

 

4 

d 

1 

 

 

4 

e 

1 

 

1 

f 

4 




Vektoren 



H3 



I1 



K1 


Kommentar 

Die Schüler/innen können z.B. in Individualarbeit die Aufgabe bearbeiten und dann in Partnerarbeit 

über die Lösungen diskutieren. 

Die Aufgabe ist für den Einsatz im Unterricht oder als Testaufgabe gedacht. 


PARALLEL ODER NORMAL 2 


 

1 

Gegeben ist der Vektor a . 

 

4 

Entscheide, ob die in der Tabelle angegebenen Vektoren zum Vektor a parallel, normal 

bzw. weder parallel noch normal sind und kreuze die richtigen Antworten an. 

Begründe deine Entscheidungen rechnerisch. 


normal 

weder 

parallel noch 

normal 

Begründung 

 

1 

b 

 

4 

 

 

2 

c 

 

8 

 

 

4 

d 

1 

 

 

 

4 

e 

1 

 

 

1 

f 

4 

 





normal 

weder 

parallel noch 

normal 

Begründung 

 

1 

b 

 

4 

1 

1 

v 

 

4 

 

4 

1 

1 

1 

16 15 0 

 

4 

 

4 

 

2 

1 

2 

c 0,5 

 

 

8 

4 

 

8 

1 

4 

v 

 

4 

d 

 

4 

1 

 

1 

1 

4 

4 4 8 0 

 

4 

1 

1 

 

4 

v 

 

 

4 

 

4 

1 

e 

1 

1 

 

4 

4 

4 0 

 

4 

1 

 

1 

1 

1 

f 1 

 

4 

4 

4 





Vektoren 



H3 



I1 



K1 


Kommentar 

Der Unterschied zur Aufgabe „Parallel oder normal 1“ besteht darin, dass die Schüler/innen ihre 

Vorgangsweise begründen müssen. Der Handlungsbereich H4 (Argumentieren und Begründen) wird 

zusätzlich angesprochen. 

Die Aufgabe ist für den Einsatz im Unterricht oder als Testaufgabe gedacht. 


PARALLEL ODER NORMAL3 


Gegeben ist der zweidimensionale Vektor a. 

Wie überprüfst du, ob ein Vektor b zum Vektor a parallel, normal bzw. weder parallel 

noch normal ist? 


Ein Vektor b ist zum Vektor a parallel, wenn gilt: 

 

 

a v b . 

 

 

. 

Ein Vektor b ist zum Vektor a normal, wenn gilt: a b 0 

Ein Vektor b ist zum Vektor a weder parallel noch normal, wenn gilt: 

 

 

a b 0 

 

 

a v b und 




Vektoren 



H3 



I1 



K1 


Kommentar 

Die Aufgabe ist für den Einsatz im Unterricht gedacht. 

Mathematische Kenntnisse müssen verbalisiert bzw. niedergeschrieben werden. 

Die Aufgabe kann als Ergänzung der Aufgaben „Parallel oder normal 1 bzw. 2“ verwendet werden. 



Gegeben sind die Geraden g: 

PARALLEL ODER SCHNEIDEND 1 

3 

2 

 

3 

a 

X t und h: X s 

2 

1 

1 

2 

Gib jeweils eine reelle Zahl a an, sodass die Geraden 

a) parallel sind. 

b) schneidend sind. 


a 

2 

a 2 t 

a) t 

2 

1 

2 t 

a 4 

b) a R\ {4} 

Anmerkung: Alle Werte außer a = 4 sind richtig zu werten. 

keine Hilfsmittel erlaubt gewohnte Hilfsmittel möglich besondere Technologie erforderlich 

Parallel oder schneidend 1 1




Vektoren 





H3 




I1 



K1 


Kommentar 

Die Serie der drei Variationen der Aufgabe „Parallel oder schneidend“ bietet die Möglichkeit die 

Lagebeziehungen von Geraden in R 2 im Unterricht auf verschiedenen Anforderungsniveaus zu 

bearbeiten. Die drei Aufgabenstellungen können für den differenzierten Unterricht bzw. zur Förderung 

von Verständnis und Nachhaltigkeit verwendet werden. 





Gegeben sind die Geraden g: 

Gibt es Zahlen 

3 

2 

 

3 

u 

X t und h: X s . 

2 

1 

1 

 

2 

u R, sodass die Geraden g und h 

a) parallel, aber nicht identisch sind? 

b) schneidend sind? 

c) identisch sind? 

Gib jeweils alle Möglichkeiten für die Zahl u an. Begründe deine Entscheidungen. 


a) Die Geraden sind parallel, aber nicht identisch, wenn die Richtungsvektoren 

parallel sind und der gegebene Punkt der Geraden h nicht auf der Geraden g liegt. 

Nachweis der Parallelität der Vektoren: 

u 2 

u 2 t 

t u 4 

 

2 

1 

2 t 

Für u = 4 sind die Richtungsvektoren der Geraden parallel. 

Überprüfung der Identität: P(3|1) in g einsetzen: 

 

3 

3 

2 

3 3 2t t 3 

t 

Pg 

1 

2 

1 

1 

2 t t 3 

Das heißt für u = 4 sind die Geraden parallel, aber nicht identisch. 

b) Damit die Geraden einen Schnittpunkt haben dürfen die Richtungsvektoren nicht 

parallel zueinander sein. Daher erhält man für u R\{4} schneidende Gerade. 

c) Dieser Fall ist für diese Angabe nicht möglich, da der gegebene Punkt P(3|1) 

der Geraden h nicht auf der Geraden g liegt. 






Vektoren 





H3 

H4 






I1 



K2 


Kommentar 


Lagebeziehungen von Geraden im R 2 im Unterricht auf verschiedenen Anforderungsniveaus zu 







3 

2 

 

3 

m 

Gegeben sind die Geraden g: X t und h: X s . 

2 

1 

1 

2 

Gibt es eine reelle Zahl m, sodass die Geraden g und h identisch sind? 

Begründe deine Überlegungen. 


Die Geraden sind identisch, wenn die Richtungsvektoren parallel sind, und der gegebene 

Punkt der Geraden h auf der Geraden g liegt. 

Für m = 4 sind die Richtungsvektoren der Geraden parallel. 

Überprüfung, ob P auf g liegt: 

P(3|1) in g einsetzen: 

 

3 

3 

2 

t 

1 

2 

1 

3 3 2t 

1 

2 t 

 

t 

3 

t 3 

Pg 

Das heißt für m = 4 sind die Geraden parallel, können aber nie identisch sein, weil P 

nicht auf g liegt. 

Oder: 

Für m = 4 sind die Richtungsvektoren der Geraden parallel. 

6 

Da der Vektor zwischen den beiden Punkten der Geraden nicht parallel zum 

2 

Richtungsvektor von g ist, kann man die Geraden durch kein reelles m „identisch 

machen“ 






Vektoren 





H3 

H4 






I1 



K3 


Kommentar 


Lagebeziehungen von Geraden in R 2 im Unterricht auf verschiedenen Anforderungsniveaus zu 




PÖSTLINGBERGBAHN 


Gegeben ist ein Streckenplan (Quelle: 

Wikipedia.org) der berühmten Pöstlingbergbahn 

in Linz. Die im Streckenplan links 

neben den Haltestellen angeführten Zahlen 

stellen die jeweilige Entfernung vom Hauptplatz 

in Kilometer (km) dar. In nachfolgenden 

Berechnungen ist näherungsweise davon 

auszugehen, dass die Streckenführung vom 

Bergbahnhof Urfahr bis hinauf auf den 

Pöstlingberg zwischen den einzelnen Stationen 

mit annähernd gleichbleibender Steigung 

verläuft. 

(Urheber: Linzer Quelle: Nikitak.de.tl-Fotograf Nikita K.) 

a) Berechne für den steilsten Abschnitt Schableder (km 2,7) bis Hoher Damm 

(km 3,0) die Steigung in Prozent und den Steigungswinkel der Bahn. 

b) In Wikipedia.org wird behauptet, dass die Steigung der Pöstlingbergbahn ab 

Bergbahnhof Urfahr fast durchgehend 10,5% beträgt. 

Wie lange müsste demnach die Höhendifferenz ab Bergbahnhof Urfahr sein, wenn 

die angegebene Streckenlänge korrekt ist? Vergleiche die angegebene Höhendifferenz 

mit der errechneten. Welche Annahme triffst du für deine Rechnung? 


Pöstlingbergbahn 1


a) 

300m 

47m 

47 

sin( α) 

300 

α 9; Steigung: tan(α) 

0,159 16% 

b) 

l 

255m 

tan( α) 10,5% α 6 

h 2900 

sin(α) 303m 

Die Höhendifferenz bei 10,5% Steigung beträgt ungefähr 303 m statt der im 

Fahrplan angegebenen 255 m. 

Annahme: Die Pöstlingbergbahntrasse verläuft geradlinig. 

Pöstlingbergbahn 2




Trigonometrie 




a) H1 

H2 

b) H1 

H3 

alltagssprachliche Formulierungen in die Sprache/Darstellung der Mathematik 

übersetzen 

mit und in Tabellen oder Grafiken operieren 

alltagssprachliche Formulierungen in die Sprache/Darstellung der Mathematik 

übersetzen 

Rechenergebnisse im jeweiligen Kontext deuten 


a) 

b) 

I1 



a) K2 Herstellen von Verbindungen 

b) K3 Einsetzen von Reflexionswissen, Reflektieren 

Kommentar 

Wesentliche Aspekte dieser Aufgabe bilden das Identifizieren relevanter Informationen in einem 

längeren kontextbezogenen Text und das Übertragen dieser Informationen in mathematische 

Darstellungen. 

Auf Grund der Textlänge und der eher ungewohnten Darstellung des Fahrplans ist diese Aufgabe als 

Unterrichtaufgabe gut, als Testaufgabe jedoch kaum geeignet. Sie kann Schüler/innen zum 

Reflektieren über notwendige Modellvereinfachungen anregen. 

Pöstlingbergbahn 3

PRIMZAHLENZUORDNUNG 


f ist eine Funktion, welche jeder natürlichen Zahl n die Anzahl der Primzahlen zuordnet, 

die kleiner oder gleich n sind. 

a) Erstelle für die Grundmenge G nN, 

1 

n 15 

n 

f(n) 

eine Wertetabelle. 

b) Schreibe die Menge W der Funktionswerte bezogen auf die Grundmenge an. 

c) Zeichne den Graphen von f(n). 


Primzahlenzuordnung 1


a) 

n 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 

f(n) 0 1 2 2 3 3 4 4 4 4 5 5 6 6 6 

b) W 0,1,2,3,4,5,6 

 

c) 





Grundbegriffe der Algebra 

Wissen über die Zahlenmengen N, Z, Q, R, verständig einsetzen können 



Zwischen tabellarischen und grafischen Darstellungen funktionaler Zusammenhänge 

wechseln können 


H1 

einen gegebenen mathematischen Sachverhalt in eine andere (tabellarische, grafische, 

symbolische, rekursive oder werkzeugspezifische) Darstellungsform übertragen; zwischen 

Darstellungen oder Darstellungsformen wechseln 


I1 

I2 

Zahlenmengen: Darstellungsformen, Grundgesetze und Rechenregeln 




K1 


Kommentar 


Die Grundlagen von verschiedenen Darstellungsformen müssen zuerst erarbeitet werden. Die Aufgabe 

erfordert gute Kenntnisse über Zahlenmengen, welche in diesem Zusammenhang vertieft werden 

können. 

Ein Punktgraph statt einer „Verbindungslinie“ soll die Grundkenntnisse erweitern und die Kenntnisse 

von Grundmengen und Wertemengen vertiefen. 

Die Aufgabe ist eher als Unterrichtsaufgabe gedacht. 


PUNKTE AUF EINER GERADEN 1 


Zur Hausübung soll überprüft werden, ob die drei Punkte A(4|3), B(1|3) und C(9|9) 

auf einer Geraden liegen. 

a) Anna rechnet: 

 

5 

AB , 

6 

5 

10 

t 

6 

12 

 

10 

BC 

 

12 

 

5 

10t 

6 12t 

 

 

1 

t 

2 

1 

t 

2 

Die drei Punkte A, B und C liegen auf einer Geraden. 

b) Tom rechnet: 

 

5 

AB 

6 

4 5 

X λ 

 

3 

6 

9 4 

5 

λ 

 

9 

 

3 

6 

 

9 4 λ ( 5) 

9 3 

λ 6 

 

 

 

λ 1 

λ 1 

Die drei Punkte A, B und C liegen auf einer Geraden. 

Erkläre die einzelnen Lösungswege. 

 


a) Anna überprüft, ob die Vektoren AB 

und BC 

zueinander parallel sind, d.h. ob der 

eine Vektor als Vielfaches des zweiten dargestellt werden kann. 

 

 

1 

Da AB BC 

gilt, liegen die Punkte auf einer Geraden. 

2 

b) Tom stellt die Gleichung der Geraden durch die Punkte A und B auf und überprüft 

durch Einsetzen des Punktes C dessen Lage bezüglich der Geraden. 

Da sich für die x und yKoordinate derselbe Parameter λ 1 

ergibt, liegt der 

Punkt C auf der Geraden durch A und B. 


Punkte auf einer Geraden 1 1




Vektoren 

Definition der Rechenoperationen mit Vektoren (Addition, Multiplikation mit einem Skalar, 

Skalarmultiplikation) kennen, Rechenoperationen verständig einsetzen und (auch 

geometrisch) deuten können 


H4 





I1 



K3 


Kommentar 

Durch das Nachvollziehen der verschiedenen Lösungswege sollen den Schülerinnen und Schülern 

unterschiedliche Lösungsstrategien verständlich gemacht werden. Das Nachdenken über die 

verschiedenen Ansätze und deren Erklärung vertieft und festigt die Kenntnisse in der Vektorrechnung. 

Die Aufgabe soll die Kommunikationsfähigkeit der Schüler/innen fördern und eignet sich auch gut für 

einen schülerzentrierten Unterricht. 

Die Serie der drei Variationen der Aufgabe „Punkte auf einer Geraden“ bietet die Möglichkeit, eine 

Fragestellung im Unterricht auf verschiedenen Anforderungsniveaus zu bearbeiten. Die drei 

Aufgabenstellungen können für den differenzierten Unterricht bzw. zur Förderung von Verständnis und 

Nachhaltigkeit verwendet werden. 




Überprüfe, ob drei Punkte A(2|1), B(3|5) und C(7|7) auf einer Geraden liegen und 

erkläre deine Vorgehensweise. 

5 

AB , 

6 


10 

5 

BC 2 

2 

AB 

12 

6 

A, B und C liegen auf einer Geraden, wenn die Vektoren AB und BC zueinander parallel 

sind, d.h. wenn der eine Vektor als Vielfaches des zweiten dargestellt werden kann. 

Da 

BC 2 

AB , liegen die Punkte A, B und C auf einer Geraden. 

oder 

2 

5 

g(A, B) : X λ 

1 

6 

Überprüfung, ob C auf g(A, B) 

7 

 

 

7 

 

 

 

2 

5 

λ 

1 

6 

 

liegt: 

7 2 λ ( 5) 

7 1 

λ 6 

λ 1 

 

λ 1 

C g 

Man stellt die Gleichung der Geraden durch die Punkte A und B auf und überprüft durch 

Einsetzen des Punktes C dessen Lage bezüglich der Geraden. 

Da sich für die x und yKoordinate derselbe Parameter λ 1 

ergibt, liegt der Punkt C 

auf der Geraden durch A und B. 



oder 

Aufgrund der „günstigen“ Koordinaten der Punkte A, B und C kann man mithilfe der 

Rasterpunkte aus der Grafik ablesen, dass die Punkte auf einer Geraden liegen. 





Vektoren 





H4 




I1 



K1 


Kommentar 

Im Unterricht kann auf die Vor- und Nachteile der verschiedenen Lösungsmöglichkeiten eingegangen 

werden. 

Die Serie der drei Variationen der Aufgabe „Punkte auf einer Geraden“ bietet die Möglichkeit, eine 







Entwickle eine Strategie um zu überprüfen, ob drei Punkte A, B und C auf einer Geraden 

liegen. 


A, B und C liegen auf einer Geraden, wenn die Vektoren AB und BC zueinander parallel 

sind, d.h. wenn der eine Vektor als Vielfaches des zweiten dargestellt werden kann. 

Wenn 

oder 

AB v BC 

gilt, liegen die Punkte auf einer Geraden. 

Man stellt die Gleichung der Geraden durch die Punkte A und B auf und überprüft durch 

Einsetzen des Punktes C dessen Lage bezüglich der Geraden. 

Wenn sich für die x und yKoordinate derselbe Parameter λ ergibt, liegt der Punkt C 

auf der Geraden durch A und B. 






Vektoren 





H4 




I1 



K1 


Kommentar 

Diese Aufgabe ist eine offene Unterrichtsaufgabe, die sich gut für kooperative Lernformen eignet. Im 

Unterricht können die Vor- und Nachteile der verschiedenen Lösungsmöglichkeiten thematisiert werden. 

Die Serie der drei Variationen der „Aufgabe Punkte auf einer Geraden“ bietet die Möglichkeit, eine 





QUADRATISCHE FUNKTIONEN 1 


Die Graphen f 1 , f 2 , f 3 quadratischer Funktionen der Form 

Parabeln (siehe Abbildung). 

f(x) ax 

2 

bx c 

sind 

Ordne in der Tabelle den vorgegebenen Bedingungen die entsprechenden Graphen zu 

und trage sie in der Tabelle ein. Kreuze die zutreffende Eigenschaft an. 

Bedingung Graph(en) Eigenschaften 

b = 0 

a > 0 

a < 0 

Der Scheitelpunkt der Parabel ist ein Hochpunkt. 

Der Graph der Funktion ist symmetrisch zur y-Achse. 

Der Scheitelpunkt der Parabel ist ein Tiefpunkt. 







Quadratische Funktionen 1 1


Bedingung Graph(en) Eigenschaften 

b = 0 f 1 

a > 0 f 1 , f 2 

a < 0 f 3 













Polynomfunktion 

n 

i 

f (x) a 

0 i x 

i 

mit 

n N 

Typische Verläufe von Graphen in Abhängigkeit vom Grad der Polynomfunktion (er)kennen 


H3 




I2 

Einfluss von Parametern 


K2 


Kommentar 

Typische Verläufe von quadratischen Funktionen in Abhängigkeit von den Parametern a, b und c sollen 

erarbeitet werden. 

Die vorliegende Aufgabe ist daher als Unterrichtsbeispiel in unterschiedlichen Formen zum Erarbeiten 

bzw. Vertiefen neuer Inhalte vorstellbar. 




Eine quadratische Funktion hat die Funktionsgleichung 

und a 0 . 

2 

f(x) ax bx c mit a, 

b, c R 

Kreuze in der Tabelle jene Eigenschaften an, die unter den angegebenen Bedingungen 

immer zutreffen. 

Bedingungen 

a < 0 und 

c > 0 

a > 0, b = 0 und 

c > 0 

c = 0 

Eigenschaften 

Der Funktionsgraph hat keine Nullstelle. 

Der Graph hat genau zwei Schnittpunkte mit der x-Achse. 

Der Funktionsgraph verläuft durch den Koordinatenursprung. 







Die unten abgebildeten Graphen quadratischer Funktionen können bei der Lösung der 

Aufgabe eine Orientierungshilfe sein. 



Bedingungen 

a < 0 und 

c > 0 

a > 0, b = 0 und 

c > 0 

c = 0 

Eigenschaften 














f (x) 

i 

n 

i 

a 

0 i x 

 

mit 

n N 



H3 tabellarisch, grafisch oder symbolisch gegebene Zusammenhänge erkennen, beschreiben 



I2 



K2 


Kommentar 

Typische Verläufe von quadratischen Funktionen in Abhängigkeit von den Parametern a, b und c sollen 

erarbeitet werden. 

Die vorliegende Aufgabe ist daher als Unterrichtsbeispiel in unterschiedlichen Formen zum Erarbeiten 

bzw. Vertiefen neuer Inhalte vorstellbar. 

Im Zusammenhang mit der Anzahl der Nullstellen kann auch eine Verbindung zur Lösungsformel für 

quadratische Gleichungen hergestellt werden. 




Die Graphen f 1 , f 2 , f 3 quadratischer 

2 

Funktionen der Form f(x) ax bx c 

sind Parabeln (siehe Abbildung). 

Ordne den Aussagen in der Tabelle 

die richtigen Begründungen und die 

entsprechenden Graphen zu. 

Aussage Graph Begründung 

Wenn a kleiner 0 

ist, dann ist der 

Scheitelpunkt der 

Parabel ein 

Hochpunkt. 

b = 0 bedeutet, 

dass der 

Funktionsgraph 

symmetrisch zur 

y-Achse verläuft. 

c = 0 bedeutet, 

dass der 


durch den Koordinatenursprung 

verläuft. 

Es gilt: f(x) = f(-x). 

Die Funktionswerte werden für wachsende |x| links 

und rechts des Scheitelpunkts immer kleiner. 

Die Richtigkeit dieser Aussage kann durch Einsetzen 

des entsprechenden Punktes in die Funktionsgleichung 

f(x) = ax² + bx + c gezeigt werden. 
















Aussage Graph Begründung 

Wenn a kleiner 0 

ist, dann ist der 

Scheitelpunkt der 

Parabel ein 

Hochpunkt. 

b = 0 bedeutet, 

dass der 


symmetrisch zur 

y-Achse verläuft. 

c = 0 bedeutet, 

dass der 


durch den Koordinatenursprung 

verläuft. 

f 3 

f 1 

f 2 
























n 

f(x) a i 

x 

i0 

i 

mit 

n N 



H4 

zutreffende und unzutreffende mathematische Argumentationen bzw. Begründungen 

erkennen; begründen, warum eine Argumentation oder Begründung (un-)zutreffend ist 


I2 



K2 


Kommentar 

Nach dem Kennenlernen typischer Verläufe von quadratischen Funktionen in Abhängigkeit von den 

Parametern a, b und c sollen für einige Fälle die entsprechenden Begründungen erarbeitet werden. 

Die vorliegende Aufgabe ist daher als Beispiel für eine schülerzentrierte Unterrichtsform gedacht. 


RECHNEN MIT VEKTOREN 1 


Gegeben sind die Vektoren 

 

 

 

r , s und t . 

Kreuze an, welche Aussagen zutreffend 

bzw. nicht zutreffend sind. 

zutreffend 

nicht zutreffend 

 

 

 

 

t s r 0 

 

 

 

 

t s r 

 

 

 

 

t s r 

 

 

 

 

t r s 

 

 

 

 

t s r 

 


zutreffend 


 

 

 

 

t s r 0 

 

 

 

 

t s r 

 

 

 

 

t s r 

 

 

 

 

t r s 

 

 

 

 

t s r 

 


Rechnen mit Vektoren 1 1




Vektoren 





H3 




I1 



K1 


Kommentar 

Diese Aufgabe erfordert das Herstellen einer Verbindung zwischen Graphik und Gleichung. Zumindest 

einmal muss der Zusammenhang geometrisch richtig erkannt werden. 

Für die weitere Vorgangsweise gibt es zwei verschiedenen Möglichkeiten: 

1) durch geometrisches Lösen mithilfe der Grafik. 

2) durch Umformungen einer als richtig erkannten Gleichung (z.B. der ersten). 

Im Unterricht sollte auf beide Lösungsmöglichkeiten eingegangen werden. 

Die Aufgabe kann sowohl als Unterrichtsaufgabe wie auch als Testaufgabe verwendet werden. 


RECHNEN MIT VEKTOREN 2 


Gegeben sind die Vektoren 

 

 

 

r , s und t . 

Kreuze an, welche Aussagen zutreffend 

bzw. nicht zutreffend sind. 

Erläutere den Unterschied zwischen den 

beiden Darstellungen. 

zutreffend 


 

 

 

 

t s r 0 

 

 

 

t s 

 

r 0 

 

 


zutreffend 


 

 

 

 

t s r 0 

 

 

 

t s 

 

r 0 

 

 

Das Ergebnis einer Vektoraddition ist ein Vektor und keine Zahl. Daher ist die richtige 

Lösung der Nullvektor und nicht die Zahl Null. 






Vektoren 





H3 




I1 



K1 


Kommentar 

Die Aufgabe soll im Unterricht eingesetzt werden um den Schülerinnen und Schülern den Unterschied 

zwischen Nullvektor und der Zahl Null bewusst zu machen. 


SCHNITTPUNKTE VON GRAPHEN 


In der Abbildung sind die Graphen zweier Funktionen mit den Gleichungen 

a 

a 

f 1 

(x) , a 0 und f2(x) 

, a 0 dargestellt. 

2 

x 

x 

Kreuze bitte die richtige Aussage an und begründe deine Entscheidung. 

Der Schnittpunkt S zweier solcher Funktionsgraphen ist immer: 

a) S(1 | 1) 

b) S(a | 1) c) S(1 | a) d) S(a | a) 


a) S(1 | 1) 

b) S(a | 1) c) S(1 | a) d) S(a | a) 

a 

x 

 

a 

a x a a x a 0 a (x 

1) 

0 x 1 

2 

x 

Für x = 1 gilt 

f1 2 

 

(x) f (x) a . 


Schnittpunkte von Graphen 1




Potenzfunktionen mit 

z 

2 

f(x ) a x b , z Z sowie f(x ) a x b 

Die Wirkung der Parameter a und b kennen und die Parameter im Kontext deuten können 

1 


H2 



I2 

gemeinsame Punkte von Funktionsgraphen 


K1 


Kommentar 

Die vorliegende Aufgabe ist als Unterrichtsbeispiel (z. B. in Form einer Partnerarbeit) zur Erarbeitung 

neuer Inhalte aber auch als Diagnoseinstrument vorstellbar. 

Die durch die Grafik bedingte „Irreführung“ zu den Lösungsvarianten S(1 | 1) oder S(a | a) ist bei dieser 

Aufgabe beabsichtigt. Im Unterricht kann dabei auf die zwei Möglichkeiten „Spezialfall“ und 

„unterschiedliche Achsenskalierung“ eingegangen werden. 

Schnittpunkte von Graphen 2

SCHULWEG 1 


Tanja erzählt von Ihrem Schulweg am letzten Mittwoch: 

Zuerst bin ich langsam von Zuhause weggegangen und habe dann bemerkt, dass ich zu 

spät zur Busstation kommen werde. Dann bin ich etwas schneller gegangen und habe 

sogar noch auf den Bus warten müssen. Mit dem Bus bin ich etwas mehr als 10 min 

gefahren, auf den letzten Metern zur Schule habe ich mit meinen Freundinnen geredet. 

a) Die nebenstehende graphische 

Darstellung veranschaulicht die 

Geschichte von Tanja; die 

zurückgelegte Strecke s (in m) 

wird dabei in Abhängigkeit von 

der Zeit t (in min) dargestellt. 

Welcher Abschnitt des Schulwegs 

von Tanja entspricht welchen 

Teilen des Funktionsgraphen? 

Ordne eindeutig - mit möglichst 

genauen Grenzen – zu. 

b) Wie lange hat Tanja auf den 

Bus gewartet? 

c) Wie lange ist sie mit dem Bus 

gefahren und welche Strecke 

hat sie mit dem Bus zurückgelegt? 

d) Madeleine sagt zu Tanja: „Von der Bushaltestelle bis zur Schule seid ihr schon 

sehr langsam gegangen.“ Wie kommt Madeleine zu der Aussage? 

e) Beate sagt: „Der Bus hat während deiner Fahrt bei keiner weiteren Haltestelle 

angehalten.“ Wie könnte Beate ihre Aussage begründen? 

Wie könnte sich die Grafik ändern, wenn nach 5 Minuten Fahrt eine Haltstelle 

angefahren wurde? 

f) Elli behauptet, dass sie sogar die Fahrgeschwindigkeit des Busses annähernd 

bestimmen kann. Wie könnte sie vorgegangen sein und zu welchem Ergebnis 

kommt sie? 


Schulweg 1 1


a) Zuerst bin ich langsam von zu Hause weggegangen - das sind die ersten 

10 Minuten. 

Dann habe ich bemerkt, dass ich zu spät zur Busstation kommen werde und bin 

ich etwas schneller gegangen - von der 10 Minute an bis zur 25 Minute. 

Dann habe ich sogar noch auf den Bus warten müssen - von der 25 Minute bis 

zur 30 Minute. 

Mit dem Bus bin ich etwas mehr als 10 Minuten gefahren - genauer: von der 

30 Minute bis zur 43 Minute. 

Auf den letzten Metern zur Schule habe ich mit meinen Freundinnen geredet 

– von der 43 Minute bis zur 49 Minute. 

b) 5 Minuten 

c) Fahrzeit: 13 min; zurückgelegte Strecke: 4750 m – 1400 m = 3350 m 

d) In 6 Minuten wurden nur 150 m zurückgelegt. 

e) In dem Abschnitt gibt es keinen Knick (Geschwindigkeit konstant) oder eine waagrechte 

Unterbrechung. 

Wird nach 5 min Fahrt eine Haltestelle angefahren, so wird bei der Graphik nach 

der Minute 35 ein kurzer waagrechter Strich sein. 

f) Mit den Angaben von c) ergibt sich eine Geschwindigkeit von: 

v = 3350:13 m/min ≈ 258 m/min ≈ 15,5 km/h; v ≈ 15,5 km/h 

Schulweg 1 2






können 


a) H3 Werte aus Tabellen oder grafischen Darstellungen ablesen, sie im jeweiligen Kontext 

deuten 

b) 

c) 

H3 tabellarisch, grafisch oder symbolisch gegebene Zusammenhänge erkennen, 


d) H3 zutreffende und unzutreffende Interpretationen erkennen 

e) 

f) H3 tabellarisch, grafisch oder symbolisch gegebene Zusammenhänge erkennen, 



a) 

b) 

c) 

d) 

e) 

f) 

I2 




a) 

b) 

c) 

d) 

e) 

f) 

K2 


Kommentar 

Aufbauend auf den Erfahrungen aus dem Mathematik- und Physikunterricht der Sekundarstufe 1 

können auch Themen wie Geschwindigkeit bei gleichförmigen Bewegungen als Steigung der linearen 

Funktion bearbeitet werden. Es ergibt sich auch die Möglichkeit auf Vereinfachungen (z.B. konstante 

Geschwindigkeit des Busses) bei graphischen Veranschaulichungen einzugehen und die Grenzen der 

Gültigkeit dieser Modellbildung aufzuzeigen. 

Das Beispiel eignet sich vor allem für eine Partnerarbeit und bietet Gelegenheit auf Vereinfachungen 

bei graphischen Veranschaulichungen einzugehen. 

Im Plenum sollte darauf geachtet werden, dass vor allem die Schüler/innen miteinander diskutieren und 

zu einer Einigung kommen. Die Lehrperson fungiert hauptsächlich als Moderator. 

Eine Erweiterung auf den eigenen Schulweg oder das Erfinden einer Geschichte zu einem 

vorgegebenen Zeit-Weg-Diagramm ist ebenfalls sehr gut für kooperative Lernformen wie Gruppen- und 

Partnerarbeit geeignet. 

Schulweg 1 3

SCHULWEG 2 


a) In der nebenstehenden Graphik wird 

der Schulweg von Ulrich veranschaulicht. 

Finde dazu eine passende Geschichte, 

wie Ulrich gegangen sein könnte. 

b) Gibt es zu der zweiten Graphik eine 

ähnliche Geschichte? 

Begründe deine Aussagen. 


a) Sinngemäß: Ulrich geht von zu Hause fort und kommt nach 10 Minuten und 600 m 

zurückgelegten Weges (Strecke AB) zu seinem Freund. Dieser ist aber noch nicht 

fertig und er muss 10 min warten (Strecke BC). Dann gehen sie gemeinsam die 

restlichen 1100 m in 15 min bis zur Schule. 

b) Sinngemäß: Der vertikale Abschnitt CD wird nicht möglich sein (keine Funktion). 

Der Abschnitt DE kann erklärt werden, etwa durch Zurückgehen Richtung 

Ausgangspunkt. (z.B.: In der Graphik wird die Entfernung von Ulrich zu seiner 

Wohnung dargestellt; die Busstation ist etwas weiter entfernt als die Schule). 


Schulweg 2 1





Aus Tabellen, Graphen und Gleichungen von Funktionen Werte(paare) ermitteln und im 




H3 


deuten 


I2 




K2 


Kommentar 

Erweiterung: Partnerarbeit 

Schüler/in A und Schüler/in B zeichnen jeweils eine Graphik auf ein Blatt, die eine Geschichte (z. B. 

Wasserstandshöhe in der Badewanne, Schulweg, Autofahrt, …) beschreibt. Dann werden die Blätter 

ausgetauscht. A schreibt nun eine Geschichte, die zur Graphik von B passt; B schreibt eine Geschichte, 

die zur Grafik von A passt. 

Die Kontrolle erfolgt durch Austausch der Blätter mit einer benachbarten Zweiergruppe, die versuchen 

muss, die Richtigkeit der Geschichte zur vorgegebenen Grafik zu überprüfen. 

Schulweg 2 2

STROMPREISE 


Ein Energieversorger bietet Kunden folgenden Tarif für Haushaltsstrom an. 

Information zu Ihrem Energieprodukt 

Preisübersicht Optima Float April 2010 

Produkt Preiskomponente Einheit Betrag 

Optima Float Energieverbrauchspreis ct / kWh* 8,3399 

Preise inkl. 20 % USt. 

* in Cent pro verbrauchter Kilowattstunde 

Grundpreis Euro/Monat 3,00 

a) Familie Kraner verbrauchte im Monat September1.020 kWh. Wie viel hätte sie mit 

diesem Tarif zu bezahlen? 

b) Stelle eine Formel zur Berechnung des monatlichen Energiegesamtpreises 

(Energieverbrauchpreis plus Grundpreis) auf und erkläre die von dir verwendeten 

Variablen. 

c) Besteht zwischen dem Verbrauch an kWh und dem monatlichen Energiegesamtpreis 

ein linearer Zusammenhang? Begründe deine Antwort. 

d) Besteht zwischen dem Verbrauch an kWh und dem Energiegesamtpreis (jeweils 

für ein Monat gerechnet) ein direktes Verhältnis? Begründe deine Antwort. 

e) Besteht zwischen dem Verbrauch an kWh und dem Preis für diese kWh (exklusive 

Grundpreis) ein direktes Verhältnis? Begründe deine Antwort. 


Strompreise 1

a) 3 1.020 0,083399 

88,867 

Familie Kraner bezahlt € 88,87. 


b) P(x) 3 x 0,083399 

x …. verbrauchte kWh, P(x) …. Preis in € 

c) Ja, weil sich eine Funktionsgleichung der Form y k x d angeben lässt, wobei 

k 0,083399 und d 3 ist. 

d) Nein, weil doppelter Verbrauch bedeutet nicht doppelter Energiegesamtpreis. 

e) Ja. Wird vom monatlich zu entrichtenden Grundpreis abgesehen, gilt: 

doppelter Verbrauch ergibt einen doppelt so hohen Energieverbrauchpreis. 

Strompreise 2





Die Angemessenheit einer Beschreibung mittels linearer Funktion bewerten können 


a) H2 elementare Rechenoperationen in den jeweiligen Inhaltsbereichen planen und 

durchführen 

b) H1 ein für die Problemstellung geeignetes mathematisches Modell verwenden oder 

entwickeln 

c) 

d) 

e) 

H4 

mathematische Argumente nennen, die für oder gegen die Verwendung eines 

bestimmten mathematischen Begriffs, eines Modells, einer Darstellung oder eines 

bestimmten Lösungswegs bzw. für oder gegen eine bestimmte Lösung oder 

Interpretation sprechen 


a) 

b) 

c) 

d) 

e) 

I2 

charakteristische Eigenschaften von linearen und quadratischen Funktionen, 

Polynomfunktionen, von einfachen rationalen Funktionen, Winkelfunktionen, Potenzund 



a) 

b) 

c) 

d) 

e) 

K3 


Kommentar 

Der Text stammt aus einem tatsächlich existierenden Schreiben der EVN und wurde so übernommen 

(einschließlich der Tabelle mit Angaben in ct und €). 

Die Aufgabe soll durch geeignete Fragestellungen den Schülerinnen und Schülern die Möglichkeit 

geben, ihre unterschiedlichen mathematischen Kompetenzen zu zeigen. 

Die Aufgabe ist eher für den Unterricht geeignet. Als Arbeitsweise wären auch Partner- oder Gruppenarbeit 

empfehlenswert. 

Strompreise 3

TEMPERATURSKALEN 1 


Temperaturen werden bei uns in °C (Celsius) gemessen; in einigen anderen Ländern ist 

die Messung in °F (Fahrenheit) üblich. 

Die Gerade f stellt den Zusammenhang zwischen °C und °F dar. 

Kreuze die richtigen Aussagen an: 

 

 

 

 

 

 

 

160°C entsprechen auch 160°F. 

160 °C entsprechen doppelt so vielen °F. 

f(x 

2 

) f(x 

1) 

320 140 

9 

Der Anstieg der Geraden ist k . 

x2 

x1 

160 60 5 

x2 x1 

5 


f(x 

2 

) f(x 

1) 

9 

Eine Zunahme um 1°F bedeutet eine Zunahme um 1,8°C. 

Eine Zunahme um 1°C bedeutet eine Zunahme um 1,8 °F. 

Eine Abnahme um 1°F bedeutet eine Abnahme um 5 °C. 9 

Temperaturskalen 1 1


 

 

 

 

 

 

 

160°C entsprechen auch 160°F. 

160 °C entsprechen doppelt so vielen °F. 

f(x 

2 

) f(x 

1) 

320 140 

9 


x2 

x1 

160 60 5 

x2 x1 

5 


f(x 

2 

) f(x 

1) 

9 

Eine Zunahme um 1°F bedeutet eine Zunahme um 1,8°C. 

Eine Zunahme um 1°C bedeutet eine Zunahme um 1,8 °F. 

Eine Abnahme um 1°F bedeutet eine Abnahme um 5 °C. 9 





Charakteristische Eigenschaften kennen und im Kontext deuten können: 

f(x2 

) f(x1 

) 

f(x 1) f(x) k ; k f 

'(x) 

x x 

2 

1 


H2 

mit und in Tabellen oder Grafiken operieren 


I2 




a) K2 Herstellen von Verbindungen 

Kommentar 

Mit Hilfe dieser Aufgabe soll der Begriff des Anstiegs einer Geraden und dessen Interpretation 

gründlich erarbeitet werden, wobei auch die Kenntnis des Differenzenquotienten wesentlich ist. 

Gefordert wird auch die Kompetenz mit unterschiedlichen Achsenskalierungen zu arbeiten. 

Wegen der letzten Aussage (Umkehrfunktion) stellt das Beispiel in dieser Form eine Erweiterung dar. 






Eine Zunahme um 1°C bedeutet eine Zunahme um 5 

9 °F. 

Eine Temperatur von 50°C entspricht einer Temperatur von 122°F. 

Gib den entsprechenden Funktionsterm an, wenn x die Temperatur in °C und f(x) die 

Temperatur in °F sein soll. 

f(x) 

9 

k 

5 

k x d 

9 

122 50 d d 32 

5 

f(x) 

 

9 

x 32 

5 







Lineare Funktion f(x ) k x d 

Verbal, tabellarisch, grafisch oder durch eine Gleichung (Formel) gegebene lineare 

Zusammenhänge als lineare Funktionen erkennen bzw. betrachten können; zwischen 

diesen Darstellungsformen wechseln können 


H1 

alltagssprachliche Formulierungen in die Sprache/Darstellung der Mathematik übersetzen 


I2 




K1 


Kommentar 

Die Funktionsgleichung f(x) = kx + d und die Bedeutung der Parameter müssen zur Lösung des 

vorliegenden Beispiels bereits bekannt sein. Unter dieser Voraussetzung kann die Aufgabe als 

Unterrichtsbeispiel zur Vertiefung – geeignet für einen schülerzentrierten Unterricht – aber auch als 

Diagnoseinstrument herangezogen werden. 

Ergänzend könnte eine grafische Darstellung verlangt werden. 






Es besteht der folgende Zusammenhang: 

9 

f(x) 

x 32 (x ... Temperatur in °C, f(x) ... Temperatur in °F) 

5 

Kreuze die richtigen Aussagen an. 

Die Temperatur in °C und jene in °F sind zueinander 

 

 

direkt proportional, da gilt: Je mehr °C, desto mehr °F. 

direkt proportional, da eine Zunahme um 1°C immer eine Erwärmung um gleich 

viele °F bedeutet. 

indirekt proportional, da es beispielsweise bei 320°F genau halb so viele °C hat. 

nicht proportional, da eine Erwärmung auf z. B. dreimal so viele °C weder bedeutet, 

dass die Temperatur auf dreimal so viele °F ansteigt, noch dass sie auf ein Drittel 

absinkt. 

nicht proportional, da der entsprechende Funktionsterm die Form f(x) 

k x d mit 

d 0 hat. 


Die Temperatur in °C und jene in °F sind zueinander 

 

 

direkt proportional, da gilt: Je mehr °C, desto mehr °F. 

direkt proportional, da eine Zunahme um 1°C immer eine Erwärmung um gleich 

viele °F bedeutet. 

indirekt proportional, da es beispielsweise bei 320°F genau halb so viele °C hat. 

nicht proportional, da eine Erwärmung auf z. B. dreimal so viele °C weder bedeutet, 

dass die Temperatur auf dreimal so viele °F ansteigt, noch dass sie auf ein Drittel 

absinkt. 

nicht proportional, da der entsprechende Funktionsterm die Form f(x) 

k x d mit 

d 0 hat. 







Direkte Proportionalität als lineare Funktion vom Typ 

f(x ) k x beschreiben können 


H3 

zutreffende und unzutreffende Interpretationen erkennen 






K3 


Kommentar 

Dieses Beispiel ist als Diskussionsgrundlage für den Unterricht gedacht. Der Begriff der direkten 

Proportionalität soll damit verständlich gemacht und vor allem der weit verbreitete Irrtum, direkte 

Proportionalität ist gleich bedeutend mit „je mehr, desto mehr“ ausgeräumt werden. 


TEMPERATURVERLAUF 


In untenstehender Graphik wird der Temperaturverlauf (T in °C) eines chemischen 

Experiments innerhalb der ersten 8 Minuten annähernd wiedergegeben. 

In der Aufgabenstellung stehen t 1 und t 2 für zwei beliebige Zeitpunkte. 

T 

a) Was wird durch T(t 1 ) bestimmt? 

b) Bestimme T(1), T(3,5), T(7,5). 

c) Erstelle eine sinnvolle Tabelle (siehe Vorlage) mit einigen Werten und mit verbalen 

Kommentaren so, dass der Temperaturverlauf schnell aus der Tabelle skizziert 

werden kann. 

t T Kommentar 

t 

d) Erkläre in Worten, was durch T(3,5) – T(1) bzw. allgemein T(t 2 ) – T(t 1 ) ausgedrückt 

wird. 

e) In welchem Intervall von einer Minute könnte die Aussage „Jetzt ändert sich die 

Temperatur aber nicht sehr stark“ bzw. „Jetzt ändert sich die Temperatur aber 

stark.“ gelten? Begründe deine Antworten. 


Temperaturverlauf 1


a) T(t 1 ) gibt die Temperatur zu dem Zeitpunkt t 1 an. 

b) Näherungswerte: T(1) = 30°, T(3,5) ≈ 25,8°, T(7,5) ≈ 25,5° 

c) 

t T Kommentar 

0 26 Startpunkt 

≈1,5 ≈30,4 Hochpunkt (oder sinngemäß) 

≈3,5 ≈25,8 Wendepunkt (oder singemäß) 

≈5,8 ≈20 Tiefpunkt (oder sinngemäß) 

8 30 Endpunkt 

d) allgemein: T(t 2 ) – T(t 1 ) gibt die Temperaturdifferenz zwischen den beiden Zeitpunkten 

t 2 und t 1 wieder 

konkret: T(3,5) – T(1) gibt die Temperaturdifferenz zwischen den Zeitpunkten t 3.5 

und t 1 wieder; sie beträgt ≈ - 4,2 ° 

e) Keine starke Änderung der Temperatur zwischen der 1. und 2. Minute, hier beträgt 

sie immer um die 30°, bzw. zwischen den Minuten 5,5 und 6,5, hier sind es immer 

um die 20°; 

eher starke Änderungen in der ersten Minute, in den Minuten 2,5 bis 6 und in der 

letzten Minute. 

Temperaturverlauf 2





Aus Tabellen, Graphen und Gleichungen von Funktionen Werte(paare) ermitteln und 

im Kontext deuten können 


können 


a) 

b) 

c) 

d) 

e) 

H3 

H3 


deuten 

tabellarisch, grafisch oder symbolisch gegebene Zusammenhänge erkennen, 



a) 

b) 

c) 

d) 

e) 

I2 wichtige Funktionseigenschaften (z.B. Nullstelle, Monotonie, Extremwert, 

Wendepunkt, Periodizität, Symmetrie) 



b) 

c) K2 Herstellen von Verbindungen 

d) K1 Einsetzen von Grundkenntnissen und Grundfertigkeiten 

e) K2 Herstellen von Verbindungen 

Kommentar 

Um Lösungen der Schüler/innen beurteilen zu können, sollen die Werte auch von der Lehrperson 

abgelesen werden. Zusätzlich wird die verwendete Funktion angegeben: 

1 

f(x) 

(x 1) (x 2) (x 8) 30 . 

4 

Der Wendepunkt wird nicht unbedingt erwartet, die Fragestellung bei e) legt eine Diskussion aber nahe. 

Die Aufgabe eignet sich vor allem für eine Partnerarbeit. Durch den Austausch von Gedanken soll ein 

intuitiver Zugang zu der Interpretation von Funktionsgraphen ermöglicht werden. Die Diskussion im 

Plenum über verschiedene Aussagen bietet für die Lehrperson die Gelegenheit, auf Differenzen 

(absolute und relative) einzugehen. 

Temperaturverlauf 3

VEKTOREN IM DREIECK 


Ein Dreieck ABC ist rechtwinklig mit der Hypotenuse AB. 

Bewerte die folgenden Aussagen und kreuze entsprechend an. 

Aussage ist immer richtig kann richtig sein stimmt sicher nicht 

AB AC 

 

AB BC AC 

 

AC BC 0 

 

AB 

2 

2 

2 

AC BC 

 

AB BC 

 

AC BC 

 


Aussage ist immer richtig kann richtig sein stimmt sicher nicht 

AB AC 

 

AB BC AC 

 

AC BC 0 

 

AB 

2 

2 

2 

AC BC 

 

AB BC 

 

AC BC 

 


Vektoren im Dreieck 1




Vektoren 






H3 




I1 



K2 


Kommentar 

Die Aufgabe kann im Unterricht zum Wiederholen und Festigen der verschiedenen Begriffe der 

Vektorrechnung wie Länge von Vektoren, Gleichheit von Vektoren, Skalarprodukt bzw. als Diagnoseinstrument 

verwendet werden. 

Durch Ergänzen einer entsprechenden Skizze kann man das Anforderungsniveau verändern und die 

Aufgabe somit auch für die Differenzierung im Unterricht einsetzen. 

Vektoren im Dreieck 2

WINKELFUNKTIONEN IM EINHEITSKREIS 


In der folgenden Abbildung sind vier Winkelfunktionswerte am Einheitskreis (farbig) 

dargestellt. 

a) Gib zu jedem dargestellten Winkelfunktionswert an, um welche Winkelfunktion es 

sich dabei handelt und ob der darstellte Funktionswert positiv oder negativ ist. 

b) Zeichne zu jedem Winkelfunktionswert alle Winkel im Einheitskreis ein, die den 

gleichen Winkelfunktionswert besitzen. Wie viele solche Winkel gibt es jeweils? 


Winkelfunktionen im Einheitskreis 1


a) I) sin( ) 0 

II) sin( ) 0 

III) cos( ) 0 

IV) tan( ) 0 

b) 

Es gibt – mit Ausnahme von Sonderfällen wie beispielsweise bei I) dargestellt – 

jeweils zwei Winkel, die im Einheitskreis den gleichen Winkelfunktionswert 

besitzen. 





Trigonometrie 

Definitionen von sin, cos für Winkel größer als 90° kennen und einsetzen können 


H3 


deuten 


I1 



K1 


Kommentar 

Die Aufgabenstellung ist für alle möglichen Winkelfunktionswerte (egal ob mit positiven oder negativen 

Vorzeichen) adaptierbar. 

Sie eignet sich auch – bei geeigneter Ausgangskonstruktion mit z.B. GeoGebra – für den computerunterstützten 

Unterricht, da dann die farbigen Winkelfunktionswerte in der Aufgabenstellung sehr leicht 

verändert und ihre Beträge angezeigt werden können. So können auch Wertebereiche der einzelnen 

Winkelfunktionen sowie Vorzeichenregeln in den vier Quadranten erarbeitet werden. 

Die in der Aufgabenstellung IV) geforderte Tangensfunktion stellt eine Erweiterung des Grundkompetenzmodells 

dar. 


WINKELFUNKTIONEN IM RECHTWINKLIGEN 

DREIECK 1 


In der folgenden Abbildung sind vier rechtwinklige Dreiecke dargestellt. 

Gib in jedem Dreieck für den bezeichneten spitzen Winkel an, welche Winkelfunktion 

durch das angegebene Seitenverhältnis dargestellt wird. 

c1 

....... 

e 

a) Dreieck 1: α 

b) Dreieck 2: β 

....... 

c) Dreieck 3: γ 

....... 

d) Dreieck 4: δ 

b 

u 

j 

k 

h 

....... 

g 

2 

3 

Winkelfunktionen im rechtwinkligen Dreieck 1_schwarz-weiß 1


a) cos α 

b) tan β 

c) sin γ 

d) sin δ 




Trigonometrie 




H3 




I1 



K1 


Kommentar 

Diese Aufgabe zielt auf die Festigung der Definition der Winkelfunktionen am rechtwinkligen Dreieck. 

Vorausgesetzt wird natürlich die Kenntnis dieser Definitionen. Didaktisch ist an einen Einsatz kurz nach 

der Einführung dieser Definitionen gedacht. 

Durch die Verwendung unüblicher Seitenbezeichnungen in rechtwinkligen Dreiecken werden die sonst 

üblichen Trainingseffekte vermieden und somit wirklich die oben angegebene Grundkompetenz trainiert. 

Die Schüler/innen festigen ihr Wissen, indem sie die Definition der Winkelfunktionen auf unterschiedliche 

Situationen übertragen. 

Zahlenangaben und Berechnungen sind dafür völlig unerheblich, wenngleich diese in Folgeaufgaben 

natürlich methodisch sinnvoll eingesetzt werden könnten. 

Dieses Beispiel ist leicht modifizier- bzw. erweiterbar. Beispielsweise könnten Schüler/innen in jedem 

Dreieck den Sinus, den Cosinus und den Tangens des jeweils angegebenen Winkel durch diverse 

vorzugebende Farbcodes kennzeichnen oder sich gegenseitig in Gruppenarbeit oder Wettbewerbsituationen 

ähnliche Aufgabenstellungen mit unorthodoxen Seitenbezeichnungen und Darstellungen 

von rechtwinkeligen Dreiecken formulieren. 

Die Aufgabe liegt in zwei Varianten, schwarz-weiß und farbig vor. 

Winkelfunktionen im rechtwinkligen Dreieck 1_schwarz-weiß 2

WINKELFUNKTIONEN IM 

RECHTWINKLIGEN DREIECK 2 


In der folgenden Abbildung sind vier rechtwinklige Dreiecke dargestellt. 

Gib in jedem Dreieck für den bezeichneten spitzen Winkel an, welche Winkelfunktion 

durch das Verhältnis der roten zur blauen Seite dargestellt wird. 

a) Dreieck 1: ...... α 

b) Dreieck 2: 

 

....... 

c) Dreieck 3: ...... γ 

d) Dreieck 4: δ 

....... 

Winkelfunktionen im rechtwinkligen Dreieck 2_farbig 1


a) cos α 

b) tan β 

c) sin γ 

d) sin δ 




Trigonometrie 




H3 




I1 



K1 


Kommentar 

Diese Aufgabe zielt auf die Festigung der Definition der Winkelfunktionen am rechtwinkligen Dreieck. 

Vorausgesetzt wird die Kenntnis dieser Definitionen. Didaktisch ist an einen Einsatz kurz nach der 

Einführung dieser Definitionen gedacht. 

Durch die Verwendung gleicher Farbcodes für den Zähler und Nenner von Seitenverhältnissen in 

rechtwinkligen Dreiecken werden die sonst üblichen Seitenbezeichnungen vermieden und somit 

wirklich die oben angegebene Grundkompetenz trainiert. Die Schüler/innen festigen ihr Wissen, indem 

sie die Definition der Winkelfunktionen auf unterschiedliche Situationen übertragen. 

Zahlenangaben und Berechnungen sind dafür völlig unerheblich, wenngleich diese in Folgeaufgaben 

natürlich methodisch sinnvoll eingesetzt werden könnten. 

Dieses Beispiel ist leicht modifizier- bzw. erweiterbar. Beispielsweise könnten Schüler/innen in jedem 

Dreieck den Sinus, den Cosinus und den Tangens des jeweils angegebenen Winkel durch diverse 

vorzugebende Farbcodes kennzeichnen oder sich gegenseitig in Gruppenarbeit oder Wettbewerbsituationen 

ähnliche Aufgabenstellungen mit Farbcodes formulieren. 


Winkelfunktionen im rechtwinkligen Dreieck 2_farbig 2

WINKELFUNKTIONEN IM RECHTWINKLIGEN 

DREIECK 3 


Gegeben ist ein rechtwinkliges Dreieck mit nebenstehender 

Skizze. 

a) Zeige, dass dieses Dreieck mit diesen Angaben 

möglich ist. 

b) Welche der folgenden Aussagen sind im oben abgebildeten 

rechtwinkligen Dreieck richtig beziehungsweise 

falsch? 

Kreuze in der Tabelle „richtig“ bzw. „falsch“ an. 

Aussage 

richtig falsch 

cos( 

sin( 

tan( 

5 

) 

13 

 

5 

) 

13 

 

5 

) 

13 

 

13 

cos( ) 

12 

 

5 

sin( ) 

13 

 

12 

tan( ) 

5 

 

sin( ) 

tan( ) 

cos( ) 

 


Winkelfunktionen im rechtwinkligen Dreieck 3 1


a) Das Dreieck kann so existieren, da der Pythagoreische Lehrsatz erfüllt ist: 

2 2 2 

15 36 39 

b) 

Beziehung richtig falsch 

cos( 

sin( 

tan( 

5 

) 

13 

 

5 

) 

13 

 

5 

) 

13 

 

13 

cos( ) 

12 

 

5 

sin( ) 

13 

 

12 

tan( ) 

5 

 

sin( ) 

tan( ) 

cos( ) 

 





Trigonometrie 




a) H4 mathematische Argumente nennen, die für oder gegen die Verwendung eines 

bestimmten mathematischen Begriffs, eines Modells, einer Darstellung oder eines 

bestimmten Lösungswegs bzw. für oder gegen eine bestimmte Lösung oder 

Interpretation sprechen 

b) H2 elementare Rechenoperationen in den jeweiligen Inhaltsbereichen planen und 

durchführen 


a) I1 Zahlenmengen: Darstellungsformen, Grundgesetze und Rechenregeln 

b) I1 Winkelmaße; sin α, cos α, tan α; Sinus- und Cosinussatz 


a) 

b) 

K1 


Kommentar 

In der Beschreibung der Grundkompetenzen werden drei Aspekte in Zusammenhang mit Trigonometrie 

genannt. Die Teilaufgabe a) versucht einerseits nachhaltiges Lernen zu fördern (Pythagoreischer 

Lehrsatz) andererseits kann man das Beispiel auch umständlicher mit Hilfe der Trigonometrie lösen, 

indem man die Summe der Winkel α + γ berechnet. Auch mit Hilfe des Einsatzes von dynamischer 

Geometriesoftware kann man die Aufgabe lösen. 

Die Teilaufgabe b) versucht speziell die Grundkompetenz „Definitionen von sin, cos, tan im rechtwinkligen 

Dreieck kennen und zur Auflösung rechtwinkliger Dreiecke einsetzen können“ anzusprechen. 

Die Schüler/innen können ausschließlich durch Kenntnis der Definitionen sin(α), cos(α), tan(α) im 

rechtwinkligen Dreieck die richtige Antwort ankreuzen. 

Die Teilaufgabe b) kann zum nachhaltigen Lernen beitragen und erscheint daher als Unterrichtsaufgabe 

und für Testsituationen besonders gut geeignet. 


WINKELFUNKTIONSWERTE 


In der folgenden Abbildung sind drei rechtwinklige Dreiecke dargestellt. 

In jedem dieser rechtwinkligen Dreiecke gibt das Verhältnis a n : b n den Tangens des 

jeweiligen Winkels α 1 , α 2 , oder α 3 an. 

Ordne in jedem Dreieck den Tangens der Winkel α 1 , α 2 , und α 3 der Größe nach. 

Was fällt dir dabei auf? Wie kannst du das begründen? 


Winkelfunktionswerte_schwarz-weiß 1


Dieses Beispiel bietet vielfältige Lösungsmöglichkeiten im Sinne unterschiedlicher 

Argumentationslinien an. Hier ist ein Lösungsweg angegeben, der für Schüler/nnen, die 

an Berechnungen gewöhnt sind, naheliegend sein könnte. Weitere Lösungsansätze sind 

im Kommentar zu finden. 

Durch den Satz des Pythagoras kann die fehlende (blaue) Seite b n der einzelnen Dreiecke 

leicht berechnet werden: 

b1 2 

3 

 

4; b 8; b 12 und somit 

3 

6 3 

tan 

2 

3 

4 

8 4 

α 

tanα 

tanα 

 

9 

 

12 

1 

 

Die Winkelfunktionswerte sind gleich, weil es sich bei den drei Dreiecken offensichtlich 

um ähnliche Dreiecke handelt (Zwei Dreiecke sind unter anderem ähnlich, wenn sie im 

Verhältnis zweier Seiten und im Gegenwinkel der größeren Seite übereinstimmen). In 

ähnlichen Dreiecken sind die Verhältnisse von zwei beliebigen, jeweils parallelen Seiten 

gleich. Aus diesem Grund müssen auch die Winkelfunktionswerte für jede beliebige 

Winkelfunktion gleich sein. Darauf basiert die Eindeutigkeit der Definition der 

Winkelfunktionen. 

3 

4 





Trigonometrie 



H4 

mathematische Vermutungen formulieren und begründen (aufgrund deduktiven, induktiven 

oder analogen Schließens) 


I1 



K1 


Kommentar 

Die Aufgabenstellung zielt auf die Eindeutigkeit der Definition der Winkelfunktionen (hier am Beispiel 

des Tangens). Sie ist leicht in Analogie auf die anderen Winkelfunktionen übertragbar. 

Neben der oben dargestellten Berechnung der einzelnen Tangenswerte bieten sich bei a) auch weitere 

Lösungswege an, die ohne explizite Berechnung auskommen. 

Beispielsweise könnten die Schüler/innen damit argumentieren, dass in den explizit angegebenen 

Seitenlängen jeweils der Sinus der einzelnen Winkel dargestellt wird. Aufgrund der offensichtlichen 

Proportionalität der Seitenlängen müssen die Sinuswerte identisch sein. Dies bedeutet wiederum, dass 

die Winkel 1 , 2 und 3 identisch sein müssen (es handelt sich ja offensichtlich um spitze Winkel). Aus 

diesem Grund müssen es auch die Tangenswerte dieser Winkel sein. 

Wenn die Schüler/innen erkennen – wie im ausgeführten zweiten Lösungsteil dargestellt – dass die 

vorliegenden Dreiecke ähnlich zueinander sein müssen, folgt daraus sofort, dass die Winkel 1 , 2 und 

3 identisch sein müssen. Und somit sind wiederum natürlich auch die Tangenswerte der Winkel gleich. 

Neben den hier angedeuteten bzw. gezeigten Lösungswegen gibt es sicher noch viele weitere korrekte 

Argumentationen, mit denen die Erkenntnis, dass die Winkelfunktionen eindeutig definiert sind, bei den 

Schülerinnen und Schülern gefestigt werden. 

Dieses Beispiel lädt die Schüler/innen also zur Diskussion über die Argumentation auf Basis der 

Definition der Winkelfunktionen ein. Es eignet sich daher zum Einsatz in einer frühen Phase nach dem 

Kennenlernen der Definition der Winkelfunktionen. 



WINKELFUNKTIONSWERTE_FARBE 


In der folgenden Abbildung sind drei rechtwinklige Dreiecke dargestellt. 

In jedem dieser rechtwinkligen Dreiecke gibt das Verhältnis der roten zur blauen Seite 

den Tangens des jeweiligen Winkels α 1 , α 2 , oder α 3 an. 

Ordne in jedem Dreieck den Tangens der Winkel α 1 , α 2 , und α 3 der Größe nach. 

Was fällt dir dabei auf? Wie kannst du das begründen? 


Winkelfunktionswerte_Farbe 1


Dieses Beispiel bietet vielfältige Lösungsmöglichkeiten im Sinne unterschiedlicher 

Argumentationslinien an. Hier ist ein Lösungsweg angegeben, der für Schüler/innen, die 

an Berechnungen gewöhnt sind, naheliegend sein könnte. Weitere Lösungsansätze sind 

im Kommentar zu finden. 

Durch den Satz des Pythagoras kann die fehlende (blaue) Seite b der einzelnen Dreiecke 

leicht berechnet werden: 

b1 2 

3 

 

4; b 8; b 12 und somit 

3 

6 3 

tan 

2 

3 

4 

8 4 

α 

tanα 

tanα 

 

9 

 

12 

1 

 

Die Winkelfunktionswerte sind gleich, weil es sich bei den drei Dreiecken offensichtlich 

um ähnliche Dreiecke handelt (Zwei Dreiecke sind unter anderem ähnlich, wenn sie im 

Verhältnis zweier Seiten und im Gegenwinkel der größeren Seite übereinstimmen). In 

ähnlichen Dreiecken sind die Verhältnisse von zwei beliebigen, jeweils parallelen Seiten 

gleich. Aus diesem Grund müssen auch die Winkelfunktionswerte für jede beliebige 

Winkelfunktion gleich sein. Darauf basiert die Eindeutigkeit der Definition der 

Winkelfunktionen. 

3 

4 





Trigonometrie 



H4 

mathematische Vermutungen formulieren und begründen (aufgrund deduktiven, induktiven 

oder analogen Schließens) 


I1 



K1 


Kommentar 

Die Aufgabenstellung zielt auf die Eindeutigkeit der Definition der Winkelfunktionen (hier am Beispiel 

des Tangens). Sie ist in Analogie leicht auf die anderen Winkelfunktionen übertragbar. 

Neben der oben dargestellten Berechnung der einzelnen Tangenswerte bieten sich bei a) auch weitere 

Lösungswege an, die ohne explizite Berechnung auskommen. 

Beispielsweise könnten die Schüler/innen damit argumentieren, dass in den explizit angegebenen 

Seitenlängen jeweils der Sinus der einzelnen Winkel dargestellt wird. Aufgrund der offensichtlichen 

Proportionalität der Seitenlängen müssen die Sinuswerte identisch sein. Dies bedeutet wiederum, dass 

die Winkel 1 , 2 und 3 identisch sein müssen (es handelt sich ja offensichtlich um spitze Winkel). Aus 

diesem Grund müssen es auch die Tangenswerte dieser Winkel sein. 

Wenn die Schüler/innen erkennen – wie im ausgeführten zweiten Lösungsteil dargestellt – dass die 

vorliegenden Dreiecke ähnlich zueinander sein müssen, folgt daraus sofort, dass die Winkel 1 , 2 und 

3 identisch sein müssen. Und somit sind wiederum natürlich auch die Tangenswerte der Winkel gleich. 

Neben den hier angedeuteten bzw. gezeigten Lösungswegen gibt es sicher noch viele weitere korrekte 

Argumentationen, mit denen die Erkenntnis, dass die Winkelfunktionen eindeutig definiert sind, bei den 

Schülerinnen und Schülern gefestigt werden. 

Dieses Beispiel lädt die Schüler/innen also zur Diskussion über die Argumentation auf Basis der 

Definition der Winkelfunktionen ein. Es eignet sich daher zum Einsatz in einer frühen Phase nach dem 

Kennenlernen der Definition der Winkelfunktionen. 



ZAHLEN 


In der folgenden Tabelle sind verschiedene Zahlen dargestellt. 

Kreuze in jeder Zeile alle zutreffenden Aussagen an. 

N Z Q R N Z Q R 

(1) 

2 

5 

(6) 3 8 

(2) 0,4 (7) 3 8 

(3) 0 , 4 (8) 

 

4 

 

(4) 1,410 -3 (9) 0 

(5) 1,410 3 (10) 


N Z Q R N Z Q R 

(1) 

2 

5 

(6) 3 8 

(2) 0,4 (7) 3 8 

(3) 0 , 4 (8) 

 

4 

 

(4) 1,410 -3 (9) 0 

(5) 1,410 3 (10) 


Zahlen 1




Grundbegriffe der Algebra 

Wissen über die Zahlenmengen N, Z, Q, R, verständig einsetzen können 


H1 


darstellen 


I1 

Zahlenmengen: Darstellungsformen, Grundgesetze und Rechenregeln 


K2 


Kommentar 

In der Beschreibung der Grundkompetenzen werden drei Aspekte in Zusammenhang mit 

Zahlenmengen genannt. Die Aufgabe versucht, genau diese anzusprechen: 

„Wissen über die Zahlenmengen N, Z, Q, R, C, …“: 

Welche Zahlenmengen gibt es überhaupt und welche Zahl gehört wohin? 

„… über Beziehungen zueinander …“: 

Es gilt die Teilmengenbeziehung N Z Q R C. Die Kenntnis dieser Beziehung ist für die 

korrekte Lösung der Aufgabe wesentlich. Nicht angesprochen werden hier die Motive für die 

Erweiterungen der einzelnen Zahlenmengen. 

„ …und über die Darstellung ihrer Elemente verständig einsetzen können.“ 

Gängige Darstellungen - Bruchdarstellung, Dezimaldarstellung, Darstellung des Stellenwertes als 

Zehnerpotenz sowie Darstellungen von Wurzeln - müssen erkannt werden. Darüber hinaus geht 

es um die Unterscheidung zwischen einer Zahl selbst und der Form ihrer Darstellung. 

Insbesondere gibt es in der Regel verschiedene Darstellungen für dieselbe Zahl. Umgekehrt ist 

jedoch nicht jeder Term sinnvoll als Darstellung einer Zahl zu interpretieren. 

Einige Teilaufgaben wie (7) und (10) sollen Diskussionen anregen und erscheinen daher besonders gut 

als Unterrichtsaufgaben geeignet, jedoch ungeeignet für etwaige Testsituationen. Analoges gilt für die 

als Erweiterung gekennzeichneten Aufgaben. 

Zahlen 2

Erweiterung 

Hinweis: Für die Beantwortung der folgenden Fragen ist teilweise ein (Internet-)Zugang 

zur Fachliteratur erforderlich. 

a) In der Regel sind in jeder Zeile mehrere Kreuze zu setzen. Warum? 

b) Vergleiche die Zahlen in (1) und (2). Was fällt dir auf? 

c) Begründe deine Antworten für die Teilaufgaben (7) und (10). 

d) Ist die Summe bzw. das Produkt zweier irrationaler Zahlen wieder eine irrationale 

Zahl? 

Zu welcher Zahlenmenge (welchen Zahlenmengen) gehören + e bzw. e? 

e) Der Verkäufer eines Elektronikmarktes behauptet: „Numerische Taschenrechner 

haben zwar eine Wurzeltaste, aber in Wahrheit können sie gar nicht mit reellen 

Zahlen rechnen.“ Hat er recht? 


a) Aufgrund der Teilmengenbeziehung N Z Q R ist jede natürliche Zahl auch eine 

ganze Zahl, jede ganze Zahl auch eine rationale Zahl und jede rationale Zahl auch 

eine reelle Zahl. 

b) 5 

2 und 0,4 sind verschiedene Darstellungen derselben Zahl. 

c) (7) Wurzeln - auch dritte Wurzeln - sind nur für nichtnegative reelle Zahlen definiert. 

Würde man in der Erklärung „Die dritte Wurzel einer reellen Zahl n ist jene 

nichtnegative reelle Zahl, deren dritte Potenz n ergibt.“ die Forderung der 

Nichtnegativität weglassen und z.B. wegen ( 2) 

3 8 auch die Umkehrung 

3 

8 2 

akzeptieren, dann müsste man damit zugleich auf die üblichen 

Rechenregeln für Potenzen verzichten, da sich sonst Widersprüche ergäben, 

z.B. 2 = 2: 

2 

3 

8 ( 8) 

1 

3 

( 8) 

2 

6 

 

( 8) 

6 2 

 

8 

6 2 

8 

2 

6 

8 

1 

3 

 

3 

8 2 

(10) (unendlich) steht für „größer als jede beliebige Zahl“ und ist selbst keine Zahl 

aus einer der hier angeführten Zahlenmengen. 

d) Summe und Produkt irrationaler zahlen müssen keineswegs wieder irrational sein. 

Z.B. ist für die beiden irrationalen Zahlen a (1 

2) und b (1 

2) 

- die Summe a + b = 2 eine natürliche Zahl und 

- das Produkt a b = 1 eine ganze Zahl. 

(Selbstverständlich sind sowohl natürliche Zahlen als auch ganze Zahlen zugleich 

reelle Zahlen, aber nicht irrational.) 

Zahlen 3

Von + e bzw. e ist bis heute nicht bekannt, ob es sich dabei um irrationale 

Zahlen handelt. (http://de.wikipedia.org/wiki/Irrationale_Zahl 06.06.2010) 

e) Numerische Taschenrechner haben für die Darstellung reeller Zahlen nur begrenzten 

Speicherplatz zur Verfügung und können daher nur mit einer endlichen Anzahl von 

Kommastellen arbeiten, also nur mit rationalen Näherungen für Wurzeln oder andere 

irrationale Zahlen. 

Insofern hat der Verkäufer recht. 

Zahlen 4

9. Schulst. (alle)

Sie wollen auch ein ePaper? Erhöhen Sie die Reichweite Ihrer Titel.

Template löschen?

Als Template speichern?