Wärmelehre: Entropie und Temperatur - E13
Wärmelehre: Entropie und Temperatur - E13
Wärmelehre: Entropie und Temperatur - E13
Sie wollen auch ein ePaper? Erhöhen Sie die Reichweite Ihrer Titel.
YUMPU macht aus Druck-PDFs automatisch weboptimierte ePaper, die Google liebt.
Experimentalphysik 1 LB WS 07/08 (Teil 12) W. Doster<br />
<strong>Wärmelehre</strong>: <strong>Entropie</strong> <strong>und</strong> <strong>Temperatur</strong><br />
1) <strong>Entropie</strong>, S [Carnot, Ct] : Mengengröße analog zu Impuls..<br />
Maß für Wärmeinhalt eines Stoffes: 1 Ct = 1 J/°K (Joule/°Kelvin)<br />
Übereinstimmung mit umgangssprachlicher “Wärme”<br />
2) <strong>Temperatur</strong>, T [°C oder °K] thermisches Potenzial<br />
analog zu elektrischem Potenzial, Druck etc<br />
Maß für Energieladung der <strong>Entropie</strong><br />
3) <strong>Entropie</strong>stromstärke: I S [Ct/s] Wärmestrom, Wärmeleitung<br />
4) Thermischer Energiestrom: I E = T · I S [ °K · Ct/s = Watt]
<strong>Entropie</strong> im Sprachgebrauch: Teil 1<br />
Hält man einen Gegenstand, z.B. ein Stück Eisen, über eine<br />
Gasflamme, so wird er wärmer, seine <strong>Temperatur</strong> steigt. In den<br />
Gegenstand strömt Wärme (= <strong>Entropie</strong>) hinein. Je mehr Wärme<br />
man in das Eisenstück hineinfließen läßt, desto höher wird seine<br />
<strong>Temperatur</strong>. Nimmt man den Gegenstand von der Flamme weg<br />
<strong>und</strong> packt ihn in Styropor ein, so bleibt die Wärme (= <strong>Entropie</strong>) in<br />
ihm drin. Teilt man ihn in zwei gleich große Teile, so steckt in<br />
jedem Teil die Hälfte der Wärme (= <strong>Entropie</strong>), die im Gegenstand<br />
insgesamt enthalten war. Die Wärme (= <strong>Entropie</strong>) ist also<br />
mengenartig. Es gibt eine Wärmedichte (= <strong>Entropie</strong>dichte).<br />
Bringt man einen warmen Gegenstand in Kontakt mit einem<br />
kalten, so fließt Wärme (= <strong>Entropie</strong>) vom warmen zum kalten,<br />
d. h. vom Gegenstand höherer zu dem niedrigerer <strong>Temperatur</strong>.<br />
Die Wärme (= <strong>Entropie</strong>) fließt umso besser, je größer die<br />
<strong>Temperatur</strong>differenz ist. Ob sie gut von einem warmen zu einem<br />
kalten Gegenstand fließt, hängt aber auch noch von der Art des
<strong>Entropie</strong> im Sprachgebrauch: Teil 2<br />
Kontakts, der Verbindung, ab. Sind die Gegenstände durch Holz<br />
verb<strong>und</strong>en, so fließt die Wärme (= <strong>Entropie</strong>) schlechter als wenn<br />
sie durch ein Metall verb<strong>und</strong>en sind. Es gibt also gute <strong>und</strong><br />
schlechte Wärmeleiter (= <strong>Entropie</strong>leiter).<br />
Hält man einmal einen Behälter mit Luft <strong>und</strong> einmal einen gleichgroßen<br />
Behälter mit Wasser über eine Flamme, so stellt man fest,<br />
daß sich die Luft schneller erwärmt, d. h. schneller eine<br />
bestimmte <strong>Temperatur</strong> erreicht als das Wasser. Man muß also in<br />
das Wasser mehr Wärme (= <strong>Entropie</strong>) hineinstecken, um diese<br />
<strong>Temperatur</strong> zu erreichen. Wasser hat eine größere Wärmekapazität<br />
(= <strong>Entropie</strong>kapazität) als Luft.<br />
Man kann einem “System” auch Wärme (= <strong>Entropie</strong>) zuführen,<br />
ohne daß es sich erwärmt. Läßt man kochendes Wasser auf der<br />
Flamme stehen, so fließt dauernd Wärme (= <strong>Entropie</strong>) in das<br />
Wasser hinein. Seine <strong>Temperatur</strong> erhöht sich nicht mehr, aber dafür<br />
wird ständig Wasser verdampft. Der Dampf muß also die<br />
Wärme (= <strong>Entropie</strong>) forttragen. Ein Gramm Dampf enthält also<br />
(viel) mehr Wärme (= <strong>Entropie</strong>) als ein Gramm flüssiges Wasser.<br />
Läßt man einen Gegenstand, den man vorher erwärmt hat, eine<br />
Weile stehen (ohne weiter zu heizen), so fließt die Wärme
<strong>Entropie</strong> im Sprachgebrauch: Teil 3<br />
(= <strong>Entropie</strong>) aus ihm heraus, sie verteilt sich in der Umgebung.<br />
Dabei verdünnt sie sich so stark, daß man nicht mehr erkennt, wo<br />
sie sich genau befindet. Trotzdem ist sie irgendwo, sie ist nicht<br />
verschw<strong>und</strong>en im Sinn von “vernichtet”, sondern nur<br />
verschw<strong>und</strong>en im Sinn von “versteckt” oder “verstreut”.<br />
Man kann Wärme (= <strong>Entropie</strong>) nicht vernichten, aber man kann<br />
sie erzeugen, z. B. in einer Flamme, in einem elektrischen<br />
Widerstand oder durch “Reibung”.<br />
Um Wärme (= <strong>Entropie</strong>) zu erzeugen, braucht man Energie. Da<br />
wir an die Erhaltung der Energie glauben, schließen wir, daß mit<br />
der Wärme (= <strong>Entropie</strong>), die von einem elektrischen Widerstand<br />
wegfließt, auch Energie wegfließt.<br />
Bemerkung:<br />
In der physikalisch-technischen Literatur wird der Begriff “Wärme”<br />
oft verwendet als “Wärmeenergie”: Q = T· S<br />
Q ist die Menge an Energie, die mit der <strong>Entropie</strong> als Energieträger<br />
transportiert wird.
T (K)<br />
Phasenübergang<br />
flüssig → gasig<br />
400<br />
Phasenübergang<br />
fest → flüssig<br />
300<br />
etwa 20 g Wasser<br />
200<br />
100<br />
0<br />
0 40 80 120 160 200<br />
S (Ct)<br />
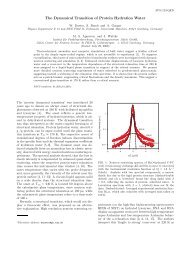
Der <strong>Entropie</strong>inhalt von 1 kg Wasserdampf ist um etwa 6000 Ct<br />
größer als der von 1 kg flüssigem Wasser.<br />
Der <strong>Entropie</strong>inhalt von 1 kg flüssigem Wasser ist um etwa 1200 Ct<br />
größer als der von 1 kg Eis.
C = dS / dT<br />
<strong>Entropie</strong>kapazität<br />
Ein Behälter enthält um so<br />
mehr <strong>Entropie</strong> S (Wärme)<br />
– je größer er ist;<br />
– je höher seine<br />
<strong>Temperatur</strong> ist.
I S = K S ∆T<br />
Ohm‘sches<br />
Gesetz<br />
K S <strong>Entropie</strong>leitfähigkeit<br />
<strong>Entropie</strong> fließt von selbst von<br />
Körpern hoher zu Körpern<br />
mit niedriger <strong>Temperatur</strong>.<br />
I S
Um <strong>Entropie</strong> von niedriger zu<br />
hoher <strong>Temperatur</strong> zu bringen,<br />
braucht man eine<br />
<strong>Entropie</strong>pumpe (Wärmepumpe).<br />
I S
Wärmepumpe<br />
T 1 T 2<br />
ENERGIE<br />
hohes Potenzial<br />
Wärmepumpe<br />
ENERGIE<br />
hohe <strong>Temperatur</strong><br />
niedriges Potenzial<br />
elektrische Ladung<br />
niedrige <strong>Temperatur</strong><br />
<strong>Entropie</strong>
Erde ist <strong>Entropie</strong>reservoir<br />
Die Umgebung nimmt <strong>Entropie</strong> auf, ohne dass sich<br />
ihre <strong>Temperatur</strong> ändert.
Die <strong>Temperatur</strong> (in absoluten Einheiten)<br />
ist eine positive Grösse:<br />
T [°K] > 0<br />
In physikalischen Gleichungen ist<br />
die <strong>Temperatur</strong> immer in absoluten<br />
Einheiten zu nehmen:<br />
I E = T I S , oder PV = nRT etc<br />
Umrechnung von °C auf °K<br />
X °K = Y °C +273,15<br />
0°C = 273,15 °K<br />
∆T: 1°C = 1°K
<strong>Entropie</strong>erzeugung <strong>und</strong> Irreversibilität
dX<br />
Physikalische Gleichung: Bilanz<br />
-<br />
dt = I X + Σ X<br />
Bilanzgleichung für X im<br />
festgelegten Raumbereich<br />
X: Maß für Menge (Energie, Stoffmenge, <strong>Entropie</strong>)<br />
I X<br />
: Stromstärke über Oberfläche<br />
Σ X<br />
: Maß für Erzeugung/Vernichtung (> 0 / < 0)<br />
X = S <strong>Entropie</strong><br />
I X<br />
Σ X<br />
dX<br />
dt<br />
Σ E = 0 Energieerhaltung<br />
Σ V = 0 Inkompressibilität:<br />
Volumen bleibt fest<br />
dS/dt = - I S + Σ S<br />
Σ S ≥ 0 2. Hauptsatz <strong>Wärmelehre</strong><br />
<strong>Entropie</strong> kann neu entstehen,<br />
also erzeugt werden bei Reibungsvorgängen.<br />
<strong>Entropie</strong>vernichtung ist aber<br />
unmöglich: Σ S < 0 wird nie beobachtet.
<strong>Entropie</strong>transport:<br />
1) konduktiv: Wärmeleitung: ∆T = R I S<br />
cond<br />
2) konvektiv: Transport von heißem Material: I S<br />
conv<br />
3) radiativ: durch elektromagnetische Strahlung
I E = - λ·A· ∆T/ ∆x<br />
I E = - α ·A·∆T<br />
Stromstärke<br />
durch Grenzfläche<br />
TK<br />
Wärmeenergie-Stromstärke durch Material<br />
∆T/ ∆x :<strong>Temperatur</strong>gradient<br />
Stahl<br />
Cu<br />
λ 2 α 12 λ 1<br />
x<br />
Thermoelemente<br />
T H<br />
Lötkolben<br />
R = 1/λ<br />
Wärmewiderstand<br />
Experiment Wärmeleitung<br />
λ: Wärme(Energie)leitfähigkeit<br />
pro Länge L<br />
α: Wärmeübergangskoeffizient
Thermische Maschinen: Wärmemotor (zyklisch)<br />
T 1<br />
T 0<br />
ENERGIE<br />
hohe <strong>Temperatur</strong><br />
Wärmemotor<br />
ENERGIE<br />
niedrige <strong>Temperatur</strong><br />
<strong>Entropie</strong><br />
Drehimpuls
ENERGIE<br />
hohe <strong>Temperatur</strong><br />
Wärmekraftwerk<br />
ENERGIE<br />
hohes Potenzial<br />
niedrige <strong>Temperatur</strong><br />
<strong>Entropie</strong><br />
niedriges Potenzial<br />
elektrische Ladung<br />
(T H – T K ) · I S = (ϕ 2 – ϕ 1 ) · I Q<br />
ENERGIE<br />
hohes Potenzial<br />
Wärmepumpe<br />
ENERGIE<br />
hohe <strong>Temperatur</strong><br />
niedriges Potenzial<br />
elektrische Ladung<br />
niedrige <strong>Temperatur</strong><br />
<strong>Entropie</strong><br />
(ϕ 2 – ϕ 1 ) · I Q = (T H – T K ) · I S
Glühwendel<br />
heiss<br />
beweglicher<br />
Kolben<br />
Kühlung<br />
Schwungrad<br />
Die Maschine kann auch als<br />
Wärmepumpe arbeiten<br />
der Stirlingmotor<br />
läuft mit „Wärme“,<br />
er setzt Energie, die von<br />
der <strong>Entropie</strong> getragen wird<br />
direkt auf den Energieträger<br />
„Impuls“ um: Im Zylinder befindet<br />
sich als Arbeitsgas Helium, das<br />
vom Kolben zwischen dem heißen<br />
<strong>und</strong> kalten Bereich hin <strong>und</strong> her<br />
geschoben wird. Dabei expandiert<br />
<strong>und</strong> kontrahiert das Gas <strong>und</strong> setzt<br />
Kolben <strong>und</strong> Schwungrad in Bewegung.<br />
E<br />
heiß<br />
kalt<br />
Wärme<br />
<strong>Entropie</strong><br />
Bewegung<br />
Impuls