Lösungen der Hausaufgaben 2/1:

Lösungen der Hausaufgaben 2/1:
zu 1.
a) f ′ (x) =5 · 2 ·
1
(
) (
tan(3x) · 1 + tan 2 1
)
(3x) · 2 = 30 ·
tan(3x) + tan(3x) ,
x ≠ k π 3 , x ≠ π (1 + 2k), k ∈ Z
6
b) f ′ (x) = 1 3 · 8x sin2 (4x) + 8x cos 2 (4x) + 2 sin(4x) cos(4x)
(
x · sin(4x) + cos(4x)
) 2
= 2 3 ·
4x + sin(4x) cos(4x)
(
x · sin(4x) + cos(4x)
) 2
,
zu 2.
x ≠ − cot(4x)
a) y = f(x) = (x + 1)(x2 − 4x + 4) (x + 1)(x − 2)2 (x + 1)(x − 2)
x 2 = = , x ≠ 2, x ≠ 3
− 5x + 6 (x − 3)(x − 2) (x − 3)
f ′ (x) = x2 − 6x + 5
(x − 3) 2 f ′′ 8
(x) =
(x − 3) 3
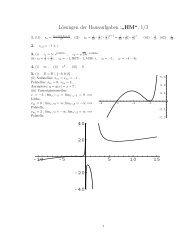
Schnittpunkt mit der y-Achse: f(0) = 2 3 ; Nullstelle bei x 0 = −1
Lücke bei ( 2; 0 )
Extrempunkte: in ( 5; 9 ) lokales Minimum; in ( 1; 1 ) lokales Maximum
Monotonie: für x ∈ ( − ∞; 1 ) und x ∈ ( 5; ∞ ) streng monoton wachsend
für x ∈ ( 1; 3 ) und x ∈ ( 3; 5 ) streng monoton fallend
Krümmung: für x > 3 konvex
für x < 3 konkav
Asymptote: y = f a (x) = x + 2
b) y = f(x) = x · e −x2 , x ∈ R
f ′ (x) = (1 − 2x 2 ) · e −x2 , x ∈ R, f ′′ (x) = (4x 3 − 6x) · e −x2 , x ∈ R,
Schnittpunkt mit der y-Achse: f(0) = 0; Nullstelle bei x 1 = 0
Extrempunkte: in ( √ √
− 2
2 ; − 2
) (
2 e− 1 √ √
2 lokales Minimum; in
2
2 ; 2
)
2 e− 1 2 lokales Maximum
Monotonie: für x ∈ ( √
− ∞; − 2
) ( √
2 und x ∈
2
2 ; ∞) streng monoton fallend
für x ∈ ( √ √
− 2
2 ; 2
)
2 streng monoton wachsend
Krümmung: für x ∈ ( √
3
−
2 ; 0) und x ∈ (√ 3
2 ; ∞) konvex
sonst konkav
Asymptote: y = 0
f(x) ist ungerade bzw. antisymmetrisch.
zu 3: y ′ = f ′ (x) = 5x 4 − 2 f ′′ (x) = 20x 3
a) y = f T (x) = 3x + 4, x ∈ R
b) k = − √ 2
√
10
; r = 10
2
≈ 1, 581 LE; M = ( 1
2 ; 1 2)
.
zu 4: f(x) = sin(πx) + 2 sin(2πx) − x 2 f ′ (x) = π cos(πx) + 4π cos(2πx) − 2x
x n+1 = x n −
sin(πxn)+2 sin(2πxn)−x2 n
π cos(πx n)+4π cos(2πx n)−2x n
n 0 1 2 3
=⇒ x ∗ ≈ 0, 55497
x n 0,50000 0,555284 0,554971 0,554971
1

zu 5. y = f(x) = x · e −x2 ,
f ′ (x) = (1 − 2x 2 ) · e −x2 ,
f ′′ (x) = (4x 3 − 6x 2 ) · e −x2 ,
x ∈ R
x ∈ R
x ∈ R
f ′′′ (x) = (−8x 4 + 24x 2 − 6) · e −x2 , x ∈ R
f (4) (x) = (16x 5 − 80x 3 + 60x) · e −x2 , x ∈ R
f(x) = x − x 3 + R 3
R 3 = (16ξ5 −80ξ 3 +60ξ)·e −ξ2
4!
x 4 , 0 < ξ < x
zu 6. R = f(R 1 ) = R 1R 2
R ′ = f ′ (R 1 ) =
R 1 + R 2
R 2 2
|∆R| ≤
(R 1 + R 2 ) 2 · |∆R 1|
2500
∣ ∣∣
|∆R| ≤
(R 1 + 500) 2 kΩ ∆R
5000
∣ ≤
R (R 1 + 500)R 1
R 2 2
(R 1 + R 2 ) 2
7. F (x) bezeichnet die Fahrzeit, wenn nach einer Fahrstrecke von x km die Straße verlassen
wird.
F (x) = x 50 + √ 1
20 (30 − x) 2 + 10 2
F ′ (x) = 1
50 − 1
20 [(30 − x)2 + 10 2 ] − 1 2 (30 − x)
√
F ′ 400
(x) = 0 =⇒ x E1 ,E 2
= 30 ±
21
√ )
F
(30 ′′ − > 0 =⇒ x ∗ = 30 −
400
21
√
400
21
≈ 25, 64 km
2