2.5. Geraden und Ebenen
2.5. Geraden und Ebenen
2.5. Geraden und Ebenen
Sie wollen auch ein ePaper? Erhöhen Sie die Reichweite Ihrer Titel.
YUMPU macht aus Druck-PDFs automatisch weboptimierte ePaper, die Google liebt.
<strong>2.5.</strong> <strong>Geraden</strong> <strong>und</strong> <strong>Ebenen</strong><br />
Parameterdarstellungen von <strong>Geraden</strong> <strong>und</strong> <strong>Ebenen</strong><br />
gewinnt man, indem man einen Ortsvektor (mit Spitze auf der <strong>Geraden</strong> oder Ebene) <strong>und</strong> einen<br />
bzw. zwei Richtungsvektoren wählt, welche die in den Nullpunkt verschobene Gerade oder Ebene<br />
aufspannen:<br />
Gerade: G = a + Ru := {a + ru : r = −∞ .. ∞}<br />
Ebene: E = a + Ru + Rv := {a + ru + sv : r, s = −∞ .. ∞}<br />
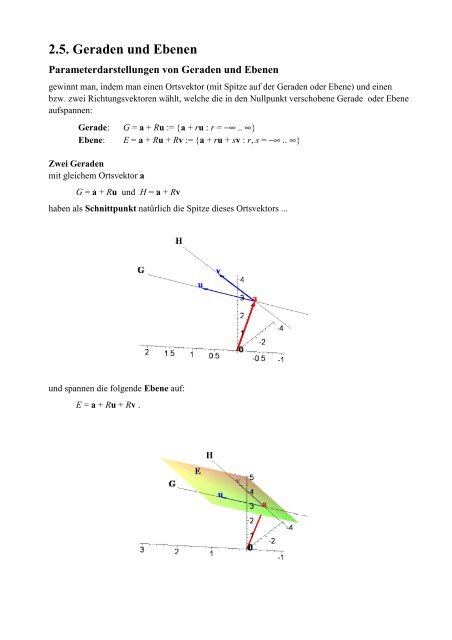
Zwei <strong>Geraden</strong><br />
mit gleichem Ortsvektor a<br />
G = a + Ru <strong>und</strong> H = a + Rv<br />
haben als Schnittpunkt natürlich die Spitze dieses Ortsvektors ...<br />
<strong>und</strong> spannen die folgende Ebene auf:<br />
E = a + Ru + Rv .
Schnittpunkt zweier <strong>Geraden</strong><br />
Sind zwei <strong>Geraden</strong><br />
G = a + Ru <strong>und</strong> H = b + Rv<br />
mit verschiedenen Ortsvektoren a <strong>und</strong> b gegeben, so muss man zur Bestimmung des Schnittpunkts<br />
(sofern er überhaupt existiert) das folgende lineare Gleichungssystem nach r <strong>und</strong> s auflösen:<br />
a + ru = b + sv (+).<br />
Das gelingt allgemein durch Normieren von u <strong>und</strong> v , d.h.durch Ersetzen von u durch u* <strong>und</strong> v<br />
durch v*, wonach man<br />
|u| =1 <strong>und</strong> |v|=1<br />
annehmen kann. Jetzt ergibt Multiplikation der vektoriellen Gleichung (+) mit u bzw. v das lineare<br />
Gleichungssystem<br />
au + r = bu + svu<br />
bv + s = av + ruv<br />
woraus man leicht r <strong>und</strong> s bestimmen kann.<br />
Im Falle uv = 0, d.h. bei aufeinander senkrecht stehenden Richtungsvektoren, ergibt sich die<br />
besonders einfache Lösung<br />
r = (b - a)u<br />
s = (a - b)v<br />
Die Winkelhalbierenden<br />
zweier von Null verschiedener Vektoren u,v (oder der durch sie verlaufenden <strong>Geraden</strong>) bestimmt<br />
man ebenfalls durch Normierung: Danach haben beide Vektoren die gleiche Länge (nämlich 1),<br />
<strong>und</strong> die Diagonalen des von ihnen aufgespannten Parallelogramms sind die Winkelhalbierenden:<br />
w(u,v) = (u* + v*)<br />
h(u,v) = (u* - v*) .<br />
Sie stehen aufeinander senkrecht, da<br />
w(u,v) h(u,v) = (u* + v*)(u* - v*) = u*u* - v*v* = 1 − 1 = 0.<br />
Für zwei <strong>Geraden</strong><br />
G = a + Ru <strong>und</strong> H = a + Rv<br />
mit Schnittpunkt a ist eine Winkelhalbierende gegeben durch<br />
W = a + R(u* + v*) ,<br />
die andere (dazu senkrechte) durch<br />
H = a + R(u* - v*) .
Beispiel 1: Winkelhalbierende in einem Dreieck<br />
Die durch den Ursprung 0 = (0,0,0) verlaufenden Seiten des Dreiecks mit den beiden weiteren<br />
Ecken<br />
u = (1,-2,2) <strong>und</strong> v = (0,1,1)<br />
haben die von folgenden Vektoren erzeugten Winkelhalbierenden:<br />
⎛ 1 2 2 ⎞ ⎛<br />
w(u,v) = (u*+ v*) = ⎜ , − , ⎟ + ⎜<br />
2 2 ⎞ ⎛<br />
⎜0,<br />
, ⎟ = ⎜<br />
1 2 2 2<br />
⎜ , − + , +<br />
⎝ 3 3 3 ⎠ ⎝ 2 2 ⎠ ⎝ 3 3 2 3<br />
⎛ 1 2 2 ⎞ ⎛<br />
h(u,v) = (u* - v*) = ⎜ , − , ⎟ − ⎜<br />
2 2 ⎞ ⎛<br />
⎜0,<br />
, ⎟ = ⎜<br />
1 2 2 2<br />
⎜ , − − , −<br />
⎝ 3 3 3 ⎠ ⎝ 2 2 ⎠ ⎝ 3 3 2 3<br />
Gleichungsdarstellung von <strong>Ebenen</strong><br />
2 ⎞<br />
⎟<br />
2 ⎠<br />
2 ⎞<br />
⎟<br />
2 ⎠<br />
<strong>Ebenen</strong> kann man auch mittels einer Gleichung definieren, indem man einen auf der Ebene<br />
senkrecht stehenden Vektor n wählt (z.B. in der Parameterdarstellung a + Ru +Rv das<br />
Vektorprodukt uxv) <strong>und</strong> dann die in der Ebene liegenden Punkte bzw. deren Orstvektoren<br />
Vektoren x durch eine der Gleichungen<br />
kennzeichnet.<br />
n(x a) = 0 oder<br />
nx = na oder<br />
nx = c (mit c = na)
<strong>Geraden</strong> in der Ebene<br />
Eine Gerade mit der zweidimensionalen Parameterdarstellung<br />
G = a + Ru = ( a1, a2 )+ R( u1, u2 )<br />
lässt sich durch eine entsprechende Gleichung beschreiben, indem man für n einen auf u = ( u1, u2 )<br />
senkrecht stehenden Vektor nimmt, z. B.<br />
n = (−u2 , u1 ) oder -n = (u2 , −u1 ) .<br />
<strong>Geraden</strong> im Raum<br />
lassen sich nicht durch eine einzige Koordinaten-Gleichung charakterisieren. Man braucht hier<br />
entweder eine vektorielle Gleichung<br />
ux(x a) = 0<br />
die besagt, daß die Vektoren zwischen zwei Punkten der <strong>Geraden</strong> stets ein Vielfaches des<br />
Richtungsvektors sind. Oder man beschreibt die Gerade durch zwei Koordinatengleichungen, was<br />
geometrisch der Tatsache entspricht, daß eine Gerade (auf viele verschiedene Weisen) als<br />
Schnittmenge zweier <strong>Ebenen</strong> darstellbar ist:<br />
Die Gerade<br />
G = a + Ru<br />
ist der Durchschnitt der <strong>Ebenen</strong><br />
E = a + Ru + Rv <strong>und</strong> F = a + Ru + Rw,<br />
sofern nicht E mit F übereinstimmt.
Schnittmenge zweier <strong>Ebenen</strong><br />
Will man sie durch Lösen von Gleichungen bestimmen, so empfiehlt es sich, eine der beiden<br />
<strong>Ebenen</strong> in Parameterform <strong>und</strong> die andere durch eine Gleichung darzustellen. Dann kann man<br />
nämlich die Parameterdarstellung in die Gleichung einsetzen:<br />
E = { a + ru + sv : r, s = - ∞ .. ∞ }<br />
F = { x : nx = c }<br />
Die Schnittmenge besteht aus den Lösungen<br />
x = a + ru + sv<br />
der Gleichung<br />
n(a + ru + sv) = c ,<br />
d. h. falls nu nicht 0 ist,<br />
r = (c - na - snv)/nu ,<br />
x = a + ((c - na)/nu)u + s(v - (nv/nu)u) ,<br />
bzw. falls nv nicht 0 ist,<br />
s = (c - na - rnu)/nv ,<br />
x = a + ((c - na)/nv)v + r(u - (nu/nv)v).<br />
Diese Formeln braucht man sich nicht zu merken, nur den Lösungsweg dorthin.<br />
Gilt sowohl nu = 0 als auch nv = 0, so sind die <strong>Ebenen</strong> parallel. (Warum?)<br />
Ist dann auch noch na = c , so sind die <strong>Ebenen</strong> sogar gleich, andernfalls ist ihr Schnitt leer.
Beispiel 2: Schnitt der Koordinatenebenen mit der Diagonalebene<br />
x1 + x2 + x3 = 1.<br />
Erste Koordinatenebene, senkrecht zur x 1 -Achse:<br />
r ( 0, 1, 0) + s ( 0, 0, 1 ) = ( 0, r, s).<br />
Schnitt ergibt<br />
r + s = 1 bzw. s = 1 − r,<br />
also die Gerade<br />
G = { ( 0, r , 1 − r), r = −∞ .. ∞ } = ( 0, 0, 1 ) + R ( 0, 1, −1 ) .<br />
Entsprechend rechnet man für die anderen Koordinatenebenen.<br />
Schnittgeraden<br />
Falls die Schnittmenge zweier <strong>Ebenen</strong> eine Gerade ist, genügt es, einen einzigen Schnittpunkt b zu<br />
kennen. Die Schnittgerade ist dann<br />
G = b + Rw,<br />
wobei man<br />
w = (nu)v (nv)u = (uxv)xn<br />
nehmen kann. Denn für dieses w gilt<br />
nw = (nu)(nv) (nv)(nu) = 0 <strong>und</strong> (uxv)w = 0,<br />
d.h. w steht senkrecht auf n <strong>und</strong> uxv ; mit anderen Worten, w liegt sowohl in der Ebene<br />
Ru + Rv<br />
als auch in der Ebene<br />
nx = 0.<br />
Ein von 0 verschiedenes Vielfaches von w tut es natürlich auch.
Parallelentest<br />
Wie prüft man, ob zwei in Parameterform gegebene <strong>Ebenen</strong><br />
E = a + Ru + Rv <strong>und</strong> F = b + Rw + Rz<br />
parallel sind? Man bildet die Normalenvektoren<br />
n = uxv , p = wxz<br />
<strong>und</strong> testet, ob diese linear abhängig sind:<br />
nxp = 0 ,<br />
oder alternativ, ob einer davon senkrecht auf den beiden anderen Richtungsvektoren steht:<br />
nw = nz = 0 .<br />
Der zweite Test ist rechnerisch meist der bequemere, weil man nur ein Kreuzprodukt zu bilden<br />
hat.<br />
Beachten Sie, daß es viele verschiedene Parameterdarstellungen bzw. Gleichungsdefinitionen für<br />
ein <strong>und</strong> dieselbe Gerade bzw. Ebene gibt. Unter allen Gleichungen, die eine Ebene bestimmen, gibt<br />
es allerdings eine besonders nützliche, die<br />
Hessesche Normalform<br />
nx = d ,<br />
wobei n ein (auf der Ebene senkrechter) Einheitsvektor (also |n|=1) <strong>und</strong> 0 ≤ d ist.<br />
In dieser Form beschreibt d den Abstand der Ebene vom Ursprung.<br />
Bei einer solchen Darstellung sind n <strong>und</strong> d eindeutig bestimmt!
Hat man eine <strong>Ebenen</strong>gleichung<br />
d.h.<br />
nx = c,<br />
n1 x1 + n2 x2 + n3 x3 = c ,<br />
in der n = ( n1, n2, n3 ) noch kein Einheitsvektor ist, dividiert man beide Seiten durch die Länge von<br />
n <strong>und</strong> erhält im Falle 0 ≤ c die Normalform<br />
n*x = nx/|n| = d<br />
bzw. in Koordinatenschreibweise:<br />
n1 x1 + n2 x2 + n3 x3 2<br />
n1 2<br />
n2 + +<br />
2<br />
n3 =<br />
2<br />
n1 c<br />
2<br />
n2 + +<br />
2<br />
n3 = d .<br />
Im Falle c < 0 muss man noch auf beiden Seiten das Vorzeichen ändern, um 0 ≤ d zu erreichen.<br />
Umformung von Parameterdarstellung in Normalform<br />
Ist eine Ebene in Parameterdarstellung gegeben, etwa<br />
E = a + Ru + Rv,<br />
so bekommt man Normalenvektoren<br />
n = (uxv)* oder n = (vxu)*<br />
(entgegengesetzte Richtungen!) <strong>und</strong> wählt denjenigen aus, für den<br />
d = na > 0<br />
gilt. Dann ist die Hessesche Normalform der Ebene E:<br />
nx = d.<br />
Zur Erinnerung:<br />
Der Flächeninhalt<br />
des von u = ( u1, u2, u3 ) <strong>und</strong> v = ( v1, v2, v3 ) aufgespannten Parallelogramms ist<br />
2<br />
u x v = ( u2 v3 − u3 v2 ) + ( u3 v1 − u1 v3 ) + ( u1 v2 − u2 v1 )<br />
<strong>und</strong> ein Normalenvektor der Länge d auf dieser Fläche ist gegeben durch<br />
nd ( u, v )<br />
⎡ d ( u ⎤<br />
= ⎢ 2 v3 − u3 v2 ) d ( u3 v1 − u1 v3 ) d ( u1 v2 − u2 v1 )<br />
⎢<br />
, ,<br />
⎥<br />
⎣ u x v<br />
u x v<br />
u x v<br />
⎦<br />
2<br />
2
Umformung einer <strong>Ebenen</strong>gleichung nx = c in eine Parameterdarstellung<br />
Man bestimmt eine spezielle Lösung<br />
a = ( a1, a2, a3 ) von nx = c (also na = c) ,<br />
indem man eine von 0 verschiedene Koordinate n i des Normalenvektors<br />
n = ( n1, n2, n3 )<br />
wählt <strong>und</strong><br />
a i<br />
=<br />
c<br />
n i<br />
sowie aj =<br />
a k = 0<br />
für die anderen beiden Koordinaten setzt. Nun ergänzt man n zu einer<br />
Orthogonalbasis (n,u,v)<br />
Sie besteht aus drei paarweise senkrechten Vektoren. Dazu wählt man beispielsweise einen<br />
beliebigen Vektor b, der kein Vielfaches von n ist, <strong>und</strong> bildet die Vektorprodukte<br />
u = nxb, v = nxu .<br />
Dann ist<br />
x = a + Ru + Rv<br />
eine Parameterdarstellung der durch die Gleichung nx = d beschriebenen Ebene.<br />
Man kann natürlich im Einzelfall auch die Gleichung<br />
n1 x1 + n2 x2 + n3 x3 = c<br />
explizit lösen, indem man eine Unbekannte x i , für die der Faktor n i nicht Null ist, isoliert, etwa<br />
x 1 =<br />
c − n2 x2 − n3 x3 n 1<br />
,<br />
<strong>und</strong> die Lösungsmenge, also die gesuchte Ebene, in folgender Parameterdarstellung mit r = x2 <strong>und</strong><br />
s = x3 bekommt:
⎛ c ⎞ ⎛ n<br />
( x1, x2, x3 ) = ⎜ , 0, 0 ⎟ + r ⎜ 2 ⎞ ⎛ n<br />
⎟ +<br />
⎝ n<br />
⎜ − , 1, 0⎟ s ⎜ 3 ⎞<br />
1 ⎠ ⎝ n<br />
⎜−<br />
, 0, 1 ⎟ .<br />
1 ⎠ ⎝ n1 ⎠<br />
Das geht in der Praxis meist schneller, liefert aber im Allgemeinen keine Orthogonalbasis.<br />
Beispiel 3: Parameterdarstellung der Diagonalebene<br />
E = {( x1, x2, x3 ) : x1 + x2 + x3 = 1}.<br />
Ortsvektor:<br />
a = ( 1, 0, 0).<br />
Normalenvektor:<br />
n = ( 1, 1, 1).<br />
Ergänzung zu einer Orthogonalbasis mittels b = ( 1, 0, 0):<br />
u = nxb = ( 0, 1, −1),<br />
v = nxu = ( −2, 1, 1).<br />
Eine von vielen Parameterdarstellungen:<br />
a + Ru + Rv<br />
= { ( 1, 0, 0) + r ( 0, 1, −1) + s ( −2, 1, 1 ) , r = −∞ .. ∞ , s = −∞ .. ∞}.