Skript Exponentialfunktion und Logarithmus.pdf - Goethe Oberschule

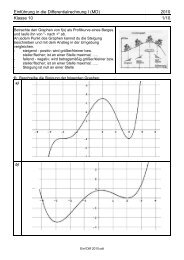
Graph zu f aus Beispiel 4.2.
Beispiel 4.3 (Tangentengleichung): Zu f(x) = e 1 2 x soll die Gleichung der Tangente
bestimmt werden, die den Graphen von f an der Stelle x 0 = 1 berührt.
Die Tangente t hat als Gerade die Funktionsgleichung t(x) = mx + n. Die Steigung m ist
gleich der Ableitung von f bei 1, es ist also m = f ′ (1) = 1 2 e 1 2 . Außerdem geht t durch den
Punkt (1|f(1)), es ist also
m · 1 + n = f(1) = e 1 2 ⇒ n = e 1 2 − m = e
1
2 −
1
2 e 1 2 =
1
2 e 1 2 .
Damit ist
t(x) = 1 2 e 1 2 x +
1
2 e 1 2 ≈ 0, 82x + 0, 82.
Bemerkung 4.1: Dasselbe Ergebnis erhält man mit Benutzung der allgemeinen Formel
t(x) = f ′ (x 0 )(x − x 0 ) + f(x 0 )
für die Tangente, die an der Stelle x 0 den Graphen von f berührt.
Graph mit Tangente zu f aus Beispiel 4.3.
Beispiel 4.4 (Funktionenschar): Gegeben ist für a ∈ R \ {0} die Funktionenschar f a
mit
f a (x) = e x − e2x
(x ∈ R).
a
Die Schar wird auf Nullstellen und Extrempunkte untersucht:
ˆ Nullstellen:
)
e x −
(1 e2x
a = 0 ⇔ ex − ex = 0 ⇔ e x = a.
a
Für a > 0 gibt es jeweils die Nullstelle x = ln a. Für a < 0 gibt es keine Nullstelle.
13