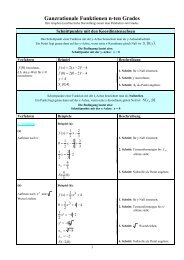
Kurvendiskussionen ganzrationler Funktionen n-ten Grades

Kurvendiskussion
1. Definitionsbereich
2. Verhalten für x → ∞
3. Symmetrie
4. Schnittpunkte mit den Koordinatenachsen
5. Ableitungen (1.-3.)
6. Extrempunkte
7. Wendepunkte – Wendetangente und Normale
8. Wertetabelle und Graph
1. Ganzrationale Funktionen n-ten Grades
Definition:
n
n−1
n−2
1
Eine Funktion f ( x)
= an x + an− 1
x + an−2x
+ ..... + a1x
+ a0
mit a
n
≠ 0 und n ∈ Ν
0
heißt
ganzrationale Funktion n-ten Grades, den Funktionsterm nennt man Polynom. Der Graph
G (Schaubild) der Funktion f heißt für n > 1 Parabel n-ter Ordnung.
f
Bezeichnung:
Der höchste Exponent gibt der Funktion den Namen!
Beispiele:
f ( x)
= 2x
−1
ganzrationale Funktion 1. Grades
f ( x)
= x²
− 3x
+ 1
ganzrationale Funktion 2. Grades
f ( x)
= 2x³
− x²
+ 1
ganzrationale Funktion 3. Grades
1 4
f ( x)
x + x³
+ 3x
= ganzrationale Funktion 4. Grades
3
f ( x)
= x(
x²
− 4)( x²
−16)
ganzrationale Funktion 5. Grades in Faktorform
1. Definitionsbereich
Bei ganzrationalen Funktionen muss kein x-Wert aus dem Definitionsbereich ausgeschlossen
werden, daher gilt immer D = R .
f max
Diesen Punkt der Kurvendiskussion kann man bei ganzrationalen Funktionen überspringen und
gleich mit Punkt 2 beginnen.
1

2. Verhalten für x → ∞ (Asymptoten)
Die Potenz mit dem höchsten Exponenten bestimmt das Verhalten des Graphen
x → ±∞
Höchster Exponent gerade!
Höchster Exponent ungerade!
G
f
für
Faktor der Potenz positiv;
x → +∞⎫
⎬y
→ +∞
x → −∞⎭
4. Grades
f
4 1
x)
=
1 x + x³
− x ²
(
8 4
Faktor der Potenz positiv;
x → +∞ ⇒ y → +∞
x → −∞ ⇒ y → −∞
3. Grades
f ( x)
= 0.1x³
+ 0.2 −1.1x
−1.2
Faktor der Potenz negativ;
x → +∞⎫
⎬y
→ −∞
x → −∞⎭
4. Grades
4
f ( x)
= −
1 ( x −15x
+ 10x)
+ 24)²
40
Faktor der Potenz negativ;
x → +∞ ⇒ y → −∞
x → −∞ ⇒ y → +∞
3. Grades
f ( x)
= −x³
+ 4x²
2

3. Symmetrie des Funktionsgraphen
Alle Exponenten bestimmen gemeinsam das Symmetrieverhalten des Funktionsgraphen
G
f
Alle Exponenten gerade!
a = mit ≠ 0
0
0
a0x
x ist gerade!
Der Funktionsgraph verläuft symmetrisch
zur y-Achse.
Alle Exponenten ungerade!
1
a1x
mit ≠ 0
x ist ungerade!
Der Funktionsgraph verläuft symmetrisch
zum Koordinatenursprung.
Achssymmetrie
Punktsymmetrie
f ( x)
= f ( x)
− für alle D
f
x ∈ f ( x)
= − f ( x)
− für alle x ∈ D
f
Achssymmetrie
4. Grades
4
f ( x)
= 0.1x
−1.7x²
+ 1.6
Punktsymmetrie
3. Grades
f
2
x)
= ( x³
− 9x)
(
3
Achssymmetrie
4. Grades
4
f ( x)
= −0.1x
+ 0.9x²
Punktsymmetrie
5. Grades
f
1
x)
= − x(
x²
−1)(
x²
− 9)
(
15
3

4. Schnittpunkte mit den Koordinatenachsen
Den Schnittpunkt einer Funktion mit der y-Achse bezeichnet man als y-Achsenabschnitt. Ein
S y
0 ; y .
Punkt liegt genau dann auf der y-Achse, wenn seine x-Koordinate gleich Null ist: ( )
Die Bedingung lautet also: Schnittpunkt mit der y-Achse: x = 0
Verfahren Beispiel Beschreibung
f (0) berechnen,
d.h. den y-Wert für x=0
ausrechnen;
f ( x)
= 2( x − 2)² − 4
f (0) = 2(0 − 2)² − 4
y = 4
S y
(0;4)
⎫
⎬
⎭
1. Schritt: für x Null einsetzen;
2. Schritt: y ausrechnen;
3. Schritt: S y als Punkt angeben;
Die Schnittpunkte einer Funktion mit der x-Achse bezeichnet man als Nullstellen. Ein Punkt liegt
N x N
;0 . Man erhält eine
genau dann auf der x-Achse, wenn seine y-Koordinate gleich Null ist: ( )
Bestimmungsgleichung n-ten Grades, die höchstens n reelle Lösungen besitzt.
Eine ganzrationale Funktion 4. Grades hat also
höchstens 4 Nullstellen,
höchstens 3 Extrempunkte, die zwischen den Nullstellen liegen müssen und
höchstens 2 Wendepunkte, die zwischen den Extrempunkten liegen müssen.
Die Verfahren zur Lösung von Gleichungen 1. und 2. Grades sind einfach und allgemein bekannt.
Die für Gleichungen 3. und 4. Grades entwickelten Lösungsverfahren sind so kompliziert, dass wir
im Allgemeinen darauf verzichten. In Sonderfällen lassen sich allerdings Gleichungen höheren
Grades auf lineare bzw. quadratische Gleichungen reduzieren, und zwar durch:
• Substitution bei biquadratischen Gleichungen;
• durch Ausklammern, wenn kein Absolutglied auftritt;
• durch Reduzierung der Gleichung auf eine niederen Grades mittels Polynomdivision oder
des Hornerschemas, falls eine Lösung bekannt ist.
Die Bedingung lautet also: Schnittpunkte mit der x-Achse: y = 0
Verfahren Beispiele Beschreibung
f ( x)
= 0 berechnen
1. Verfahren:
(a)
Auflösen nach x ;
Beispiel (a):
1 2
f ( x)
= x −
2 3
1 2 2
0 = x − +
2 3 3
1
2
x =
2
3
4
xN =
3
4
N(
;0)
3
⋅ 2
⎫
⎪
⎪
⎬
⎪
⎪
⎪⎭
1. Schritt: für y Null einsetzen;
2. Schritt: Termumformungen bis x
N
alleine steht;
3. Schritt: Nullstelle als Punkt angeben;
4

Verfahren Beispiele Beschreibung
(b)
Beispiel (b):
n
Auflösen nach x und n
Wurzel ziehen;
f ( x)
=
0 =
1
2
1
2
x³
= −4
⋅ 2
x³
= −8
x
x
N
N
= 3 − 8
= −2
N(
−2;0)
1
x
3
+ 4
2
x
3
+ 4 − 4
3
⎫
⎪
⎬
⎪
⎭
⎫
⎪
⎬
⎪
⎭
1. Schritt: für y Null einsetzen;
2. Schritt: Termumformungen bis x³
alleine steht;
3. Schritt: 3 Wurzelziehen;
4. Schritt: Nullstelle als Punkt angeben;
(c)
Beispiel (c):
Auflösen nach dem Binom
n
( x ± b)
und n Wurzel
ziehen;
f ( x)
= 2( x − 2)² − 8
0 = 2( x − 2)² − 8 + 8
+ 8 = 2( x − 2)² ÷ 2
4 = ( x − 2)² ±
±
4 = x − 2
± 2 = x − 2 + 2
x
x
x
N1/
2
N1
N 2
= ± 2 + 2
= −2
+ 2 = 0
= + 2 + 2 = 4
⎫
⎪
⎬
⎪
⎪
⎭
⎫
⎪
⎬
⎪
⎪
⎭
1. Schritt: für y Null einsetzen;
2. Schritt: Termumformungen bis (x-2)²
alleine steht;
3. Schritt: ± Wurzel ziehen;
4. Schritt: Termumformungen bis
x
N1/ 2
alleine steht;
N
1( 0;0); N
2
(4;0)
5. Schritt: Nullstellen als Punkte
angeben;
2. Verfahren:
Beispiel (a):
(a)
Ausklammern,
d.h. auf Produkt- bzw.
Faktorform bringen;
Regel:
Ein Produkt wird nur dann
Null, wenn einer der
Faktoren Null wird.
f ( x)
= 2x
0 = 2x
x²
= 4 ±
= −2
= + 2
5
− 8x³
8 = 2x²
÷ 2
− 8x³
0 = x³
⋅ (2x²
− 8) ⇒ x
0 = 2x²
− 8 + 8
x
x
N 4
N 5
5
N1/
N
1/ 2 / 3(0;0) Sattelpunkt;
N −2;0);
N ( 2;0)
4
(
5
+
2 / 3
= 0
⎫
⎪
⎬
⎪
⎭
1. Schritt: für y Null einsetzen;
3
2. Schritt: x ausklammern ⇒
dreifache Nullstelle ⇒
Terrassen- bzw. Sattelpunkt;
3. Schritt: Klammerausdruck Null
setzen
4. Schritt: Termumformungen bis x²
alleine steht;
5. Schritt: ± Wurzel ziehen;
6. Schritt: Nullstellen als Punkte
angeben;
5

Verfahren Beispiele Beschreibung
(b)
Faktorform liegt schon vor;
Regel:
Ein Produkt wird nur dann
Null, wenn einer der
Faktoren Null wird.
3. Verfahren:
Beispiel (b):
f ( x)
= (3x
+ 1) ⋅ (4x
+ 6)
0 = (3x
+ 1) ⋅ (4x
+ 6)
0 = (3x
+ 1) −1
⎫
−1
= 3x
÷ 3
⎪ ⎬
1
x
1
= −
⎪
N ⎭
3
0 = (4x
+ 6)
⎫
− 6 = 4x
÷ 4
⎪
⎬
6 3
⎪
xN
2
= − = −
⎭
4 2
1 3
N1(
− ;0); N
2
( − ;0)
3 2
Beispiel (a)
1. Schritt: für y Null einsetzen;
2. Schritt: 1. Klammerausdruck Null
setzen;
3. Schritt: Termumformungen bis x
alleine steht;
4. Schritt: 2. Klammerausdruck Null
setzen;
5. Schritt: Termumformungen bis x
alleine steht;
6. Schritt: Nullstellen als Punkte
angeben;
(a)
abc-Formel
x
1/ 2
− b ±
=
anwenden;
oder
b²
− 4ac
2a
f ( x ) = 12 x ² + 5 x −
0 = 12x²
+ 5x
− 3
a = 12; b = 5; c = −3
x
N1/
2
− 5 ±
=
2 ⋅12
− 5 ± 25 + 144)
xN1/
2
=
24
− 5 ± 13
xN1/
2
=
24
− 5 −13
3
xN1
= = − = −0,75
24 4
− 5 + 13 8 1
xN
2
= = =
24 24 3
3 1
N1(
− ;0); N
2
( ;0)
4 3
3
5² − 4 ⋅12
⋅ ( −3)
⎫
⎪
⎪
⎪
⎪
⎬
⎪
⎪
⎪
⎪
⎭
1. Schritt: für y Null einsetzen;
2. Schritt: aus der Gleichung a, b und c
ablesen;
3. Schritt: für a, b und c die Zahlen
einschließlich Vorzeichen in
die Formel einsetzen;
4. Schritt: xN1/
2
ausrechnen;
5. Schritt: Nullstellen als Punkte
angeben;
(b)
Beispiel (b)
pq-Formel
x
1/ 2
p
= − ±
2
anwenden;
2
⎛ p ⎞
⎜ ⎟
⎝ 2 ⎠
− q
f ( x)
= x²
− 5x
+ 6
0 = x²
− 5x
+ 6
p = −5;
q = + 6
2
( −5)
⎛ − 5 ⎞
x N1 / 2 = − ± ⎜ ⎟ − ( + 6)
2 ⎝ 2 ⎠
1. Schritt: für y Null einsetzen;
2. Schritt: aus der Normalform p und q
ablesen;
3. Schritt: für p und q die Zahlen
einschließlich Vorzeichen in
die Formel einsetzen;
6

Verfahren Beispiele Beschreibung
5 25 − 24
⎫
xN1/
2
= ±
⎪
2 4
⎪
⎪
5 1
xN1/
2
= ±
⎪
2 2
⎪
⎬
5 1 4
xN1
= − = = 2
⎪
2 2 2
⎪
⎪
5 1 6
⎪
xN
2
= + = = 3
⎪
2 2 2
⎪⎭
N (2;0); N (3;0)
1
2
4. Schritt: xN1/
2
ausrechnen;
5. Schritt: Nullstellen als Punkte
angeben;
(c)
Beispiel (c)
Bi-quadratische Funktionen
2n
f ( x)
= ax
n
+ bx + c :
Substitution
durchführen und lösen;
pq-Formel
oder
abc-Formel
anschließend die
Substitution rückgängig
machen;
Die Substitutionsgleichung
entscheidet welche Wurzel
man ziehen muss und
damit auch wie viele
Lösungen es gibt!
4
f ( x)
= x − 5x²
+ 6
Substitution : z = x²
f ( z)
= z²
− 5z
+ 6
0 = z²
− 5z
+ 6
p = −5;
q = + 6
siehe auch Beispiel (b): gleicher
Lösungsweg für z;
z
z
z
1/ 2
1
2
( −5)
= − ±
2
= 2
= 3
Re−
Substitution : x²
= z
x²
= 2 ⇒ x
x
x
N1
N 2
2
2
x²
= 3 ⇒ x
x
x
N 3
N 4
N ( −
1
N ( −
3
= −
= +
= −
= +
3
3
N1/
2
3 / 4
2;0); N
3;0); N
= ±
2
4
(
(
2
⎛ − 5 ⎞
⎜ ⎟ − ( + 6)
⎝ 2 ⎠
= ±
3
2
2;0);
3;0);
⎫
⎬
⎭
⎫
⎪
⎪
⎪
⎪
⎪
⎪
⎬
⎪
⎪
⎪
⎪
⎪
⎪
⎭
⎫
⎬
⎭
1. Schritt: Substitutionsgleichung
aufstellen;
2. Schritt: Funktion umschreiben;
3. Schritt: für y Null einsetzen;
4. Schritt: aus der Normalform p und q
ablesen;
5. Schritt: für p und q die Zahlen
einschließlich Vorzeichen in
die Formel einsetzen;
6. Schritt: z
N1/ 2
ausrechnen;
7. Schritt: Ergebnisse in die
Substitutionsgleichung
einsetzen und ± Wurzel
ziehen;
8. Schritt: Nullstellen als Punkte
angeben;
4. Verfahren:
Beispiel (a):
(a)
Erste Nullstelle raten,
anschließend
f ( x)
= x³
+ 10x²
+ 7x
−18
0 = x³
+ 10x²
+ 7x
−18
x
N1
= 1 geraten
1. Schritt: für y Null einsetzen;
2. Schritt: erste Nullstelle raten,
Teiler von 18!
7

Verfahren Beispiele Beschreibung
⎫
Probe:
⎪
⎬
0 = (1)³ + 10(1)² + 7(1) −18
⎪
⎭
3. Schritt: Probe durchführen;
0 ≡ 0
⎫
Polynomdivision
durchführen
( x³
+ 10x²
+ 7x
−18)
: ( x −1)
= x²
+ 11x
+ 18 ⎪
⎪
− ( x³
− x²)
⎪
⎪
0 + 11x²
+ 7x
⎬
Restpolynom r(x) bestimmt
das weitere Vorgehen:
In diesem Beispiel kann
man das Restpolynom mit
der
pq-Formel
oder
abc-Formel
lösen.
oder
− (11x²
−11x)
0 + 18x
−18
− (18x
−18)
0
r(
x)
= x²
+ 11x
+ 18
0 = x²
+ 11x
+ 18
p = + 11; q = + 18
11
11
xN
2 / 3
= − ± (
2
) ² −18
2
11 7
xN
2
= − − = −9
2 2
11 7
xN
3
= − + = −2
2 2
N (1;0); N ( −9;0);
N ( −2;0);
1
2
3
⎪
⎪
⎪
⎪
⎪
⎭
⎫
⎪
⎪
⎪
⎪
⎬
⎪
⎪
⎪
⎪
⎭
4. Schritt: Polynomdivision
durchführen;
Polynomdivision muss aufgehen!
5. Schritt: Restpolynom ablesen;
6. Schritt: Restpolynom Null setzen;
7. Schritt: aus der Normalform p und q
ablesen;
8. Schritt: für p und q die Zahlen
einschließlich Vorzeichen in
die Formel einsetzen;
9. Schritt: xN 2 / 3
ausrechnen;
10. Schritt: Nullstellen als Punkte
angeben;
(b)
Erste Nullstelle raten,
anschließend,
Hornerschema anwenden;
Beispiel (b):
f ( x)
= x³
+ 10x²
+ 7x
−18
0 = x³
+ 10x²
+ 7x
−18
x
N1
= 1 geraten
x x³ x² x c f(x)
1 10 7 -18
x=1 f(1)=
r(x) x² x c
x x³ x² x c f(x)
1 10 7 -18
x=1 1 11 18 0 f(1)=0
r(x) x² x c
1. Schritt: für y Null einsetzen;
2. Schritt: erste Nullstelle raten,
Teiler von 18!
3. Schritt: Tabelle anfertigen;
4. Schritt:
Koeffizienten einschließlich
Vorzeichen eintragen, alle Potenzen
von x müssen vorkommen, für fehlende
Potenzen wird 0 eingetragen!
5. Schritt: blaue Zellen wie folgt
ausrechnen:
1. Zelle: wird von obendrüber
abgeschrieben 1;
2. Zelle: 1*1+10=11
(x mal Zelle 1+obendrüber=Zelle 2)
3. Zelle: 1*11+7=18
(x mal Zelle 2+obendrüber=Zelle 3)
4. Zelle: 1*18-18=0
(x mal Zelle 3+obendrüber=Zelle 4)
8

Verfahren Beispiele Beschreibung
Restpolynom r(x) bestimmt
das weitere Vorgehen:
In diesem Beispiel kann
man das Restpolynom mit
der
pq-Formel
oder
abc-Formel
lösen.
r(
x)
= x²
+ 11x
+ 18
0 = x²
+ 11x
+ 18
p = + 11; q = + 18
11
11
xN
2 / 3
= − ± (
2
) ² −18
2
11 7
xN
2
= − − = −9
2 2
11 7
xN
3
= − + = −2
2 2
N (1;0); N ( −9;0);
N ( −2;0);
1
2
3
⎫
⎪
⎪
⎪
⎬
⎪
⎪
⎪
⎭
6. Schritt: Restpolynom ablesen;
7. Schritt: Restpolynom Null setzen;
8. Schritt: aus der Normalform p und q
ablesen;
9. Schritt: für p und q die Zahlen
einschließlich Vorzeichen in
die Formel einsetzen;
10. Schritt: xN 2 / 3
ausrechnen;
11. Schritt: Nullstellen als Punkte
angeben;
Faktorform:
Sind alle Nullstellen
x x x ;... x
N1 ;
N 2;
N 3 Nn
einer Funktion n-ten Grades ermittelt, so lässt sich der
Funktionsterm in Faktorform (Produkt aus linearen Faktoren) darstellen:
f ( x)
= a
a
n
n−1
n−2
1
n
x + an− 1
x + an−2x
+ ..... + a1x
+
0
=
a
n
( x − xN1 x − xN
2
x − xN
3
⋅ ⋅ x − xN
( n−
1)
x − xNn
= )( )( ) ... ( )( )
Beispiele:
Die Gleichung 1 2
³ − 4x²
+ 6x
= 0
gilt:
x hat die Lösungen (Nullstellen) x ; x = 2; x 6
f
(
2
2
1
x)
= 1 x³
− 4x²
+ 6x
= ⋅ x ⋅ ( x − 2) ⋅ ( x − 6)
N1 = 0
N 2 N 3
=
Ist die ganzrationale Funktion in Faktorform gegeben, so können die Nullstellen sofort abgelesen
werden. Die Funktion
f ( x)
= ( x + 1)( x − 4)( x − 5) hat die Nullstellen − ; x = 4; x 5
x .
N1 = 1
N 2 N 3
=
. Also
Für den Verlauf des Funktionsgraphen bedeutet eine
• „einfache Nullstelle“ z.B. Faktor (x-k): Der Graph schneidet die x-Achse bei x N
= k .
• „doppelte Nullstelle“ z.B. Faktor (x-k)²: Der Graph berührt die x-Achse bei x N
= k
.
1 ;2
N / 0) ist ein Extrempunkt (horizontale Tangente), man nennt
( k
1;2 diesen Punkt Berührpunkt.
• „dreifache Nullstelle“ z.B. Faktor (x-k)³: Der Graph schneidet die x-Achse bei x N
= k .
1; 2;3
N / 0) ist ein Wendepunkt mit horizontaler Tangente, man
( k
1;2;3 nennt diesen Punkt Sattel- oder Terrassenpunkt.
9

Beispiele:
3. Grades
f
x)
= 1 x(
x + 2)( x − 4)
(
5
4. Grades
f
x)
= 1 x(
x + 4)( x − 2)( x − 4)
(
20
3. Grades
f
1
x)
= − ( x + 2)²( x − 3)
(
10
4. Grades
f
1
x)
= ( x + 3)²( x − 3)²
(
20
3. Grades
f
1
x)
= ( x − 2)³
(
4
4. Grades
f
1
x)
= − ( x + 2)³( x − 4)
(
40
10

5. Ableitungen
Ganzrationale Funktionen leitet man nach folgenden Regeln ab:
Potenzregel
Faktorregel
Summenregel
f =
n
( x)
x mit n ∈ N
f =
n
( x)
ax mit N
f +
n ∈ und a ∈R
n m
( x)
= x x mit n,
m∈
N
⇔
⇔
⇔
f '( x)
= nx
n−1
f '( x)
= anx
f '( x)
= nx
n−1
n − 1
+
mx
m−1
Meist genügen die ersten drei Ableitungen.
Beispiel:
f ( x)
= 2x
f '( x)
= 8x³
+ 21x²
−10x
f ''( x)
= 24x²
+ 42x
−10
f '''( x)
= 48x
+ 42
f ''''( x)
= 48
f
V
( x)
= 0
4
+ 7x³
− 5x²
( n+
1)
Für die (n+1)-te Ableitung einer ganzrationalen Funktion n-ten Grades gilt: f ' ( x)
= 0
6. Extrempunkte
1. Notwendige Bedingung: f '(
x E
) = 0
Die erste Ableitung liefert alle x-Werte einer Funktion, die eine horizontale Tangente
(Steigung m=0) besitzen. Extrempunkte haben ebenfalls horizontale Tangenten, daher
liefert die erste Ableitung auch die x-Werte der Extrempunkte.
>
2. Hinreichende Bedingung: f ''( x E
)
<
0 oder Vorzeichenwechsel bei f '(
xE
)
Da man mit der ersten Ableitung alle Stellen mit horizontalen Tangenten findet, also auch
Sattelpunkte, muss man nun mit der zweiten Ableitung oder mit einem Vorzeichenwechsel
bei der ersten Ableitung prüfen, ob ein Extrempunkt vorliegt.
f ''(
) ≠ 0 oder Vorzeichenwechsel bei f '(
x ) es liegt ein Extrempunkt vor;
x E
E
11

f ''(
x E
) > 0 lokales Minimum, der Extrempunkt ist ein Tiefpunkt;
''(
) < 0
f lokales Maximum, der Extrempunkt ist ein Hochpunkt.
x E
3. y-Werte
Einsetzen von
x in (x)
E
f ergibt
E
y und man erhält x E
/ y )
E .
(
E
7. Wendepunkte – Wendetangente und Normale
1. Notwendige Bedingung: f ''(
x W
) = 0
Die zweite Ableitung liefert alle x-Werte einer Funktion, bei denen sich das
Krümmungsverhalten ändert (Übergang von einer Rechtskurve in eine Linkskurve oder
umgekehrt), daher liefert die zweite Ableitung auch die x-Werte der Wendepunkte.
2. Hinreichende Bedingung: f '''(
x W
) ≠ 0 oder Vorzeichenwechsel bei f ''(
xW
)
Mit der dritten Ableitung oder mit einem Vorzeichenwechsel bei der zweiten Ableitung prüft
man, ob ein Wendepunkt vorliegt.
f '''(
) ≠ 0 oder Vorzeichenwechsel bei f ''(
x ) es liegt ein Wendepunkt vor.
x W
3. y-Werte
Einsetzen von
W
x in (x)
f ergibt
W
y und man erhält x W
/ y )
W
W .
(
W
Wendetangente und Normale
Eine Wendetangente ist diejenige Tangente, die den Graph der Funktion im Wendepunkt berührt.
Ihre Gleichung erhält man über die Punkt-Steigungsform der Geradengleichung. Die Koordinaten
des Punktes liefert der Wendepunkt W ( x W
/ yW
) , die dazugehörige Tangentensteigung liefert die
erste Ableitung f '(
x W
) = m und es gilt:
T
f x)
= m ( x − x ) + y
T
( Wendetangente
T
Die Normale im Wendepunkt steht senkrecht auf der Wendetangente, für das Produkt der
Steigungen gilt daher: m
T
⋅ mN
= −1. . Die Koordinaten des Punktes liefert wieder der
Wendepunkt W x W
/ y ) und es gilt:
(
W
f x)
= m ( x − x ) + y
N
N
W
W
( Normale im Wendepunkt
W
W
8. Wertetabelle und Graph
Man erstellt unter Verwendung der bisher berechneten Punkte eine Wertetabelle und berechnet
gegebenenfalls Zwischenwerte um anschließend genauer zeichnen zu können.
Wertetabelle
y-Achsenabschnitt Nullstellen Extrempunkte Wendepunkte
x 0 x
N
f (x) f (0)
f x ) f x ) f x )
( N
x
E
( E
x
W
( W
Graph
G
f
der Funktion
12

G
f
ist der Graph (Schaubild) der Funktion. Man erhält G
f
, indem man die Punkte aus der
Wertetabelle in ein Koordinatensystem einträgt. Man achtet dabei auf die geeignete Wahl der
Längeneinteilung der Koordinatenachsen.
Beispiel:
f
(
4
4 1
x)
= 1 8
x + x³
− x ² ist eine ganzrationale Funktion 4.Grades, ihr Graph
f
G ist:
13