For printing - MSP
For printing - MSP
For printing - MSP
You also want an ePaper? Increase the reach of your titles
YUMPU automatically turns print PDFs into web optimized ePapers that Google loves.
IMAGINARY QUADRATIC FIELDS 17<br />
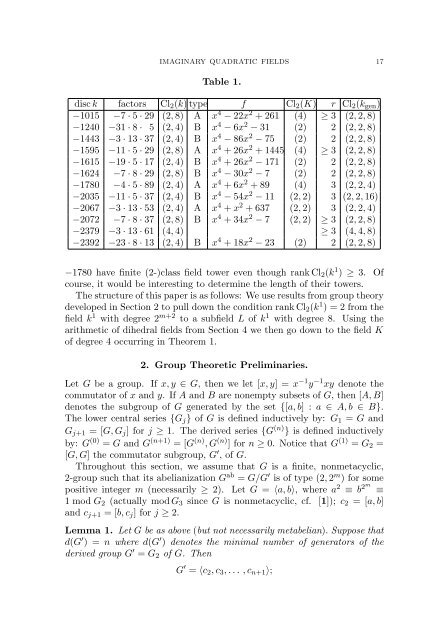
Table 1.<br />
disc k factors Cl2(k) type f Cl2(K) r Cl2(kgen)<br />
−1015 −7 · 5 · 29 (2, 8) A x 4 − 22x 2 + 261 (4) ≥ 3 (2, 2, 8)<br />
−1240 −31 · 8 · 5 (2, 4) B x 4 − 6x 2 − 31 (2) 2 (2, 2, 8)<br />
−1443 −3 · 13 · 37 (2, 4) B x 4 − 86x 2 − 75 (2) 2 (2, 2, 8)<br />
−1595 −11 · 5 · 29 (2, 8) A x 4 + 26x 2 + 1445 (4) ≥ 3 (2, 2, 8)<br />
−1615 −19 · 5 · 17 (2, 4) B x 4 + 26x 2 − 171 (2) 2 (2, 2, 8)<br />
−1624 −7 · 8 · 29 (2, 8) B x 4 − 30x 2 − 7 (2) 2 (2, 2, 8)<br />
−1780 −4 · 5 · 89 (2, 4) A x 4 + 6x 2 + 89 (4) 3 (2, 2, 4)<br />
−2035 −11 · 5 · 37 (2, 4) B x 4 − 54x 2 − 11 (2, 2) 3 (2, 2, 16)<br />
−2067 −3 · 13 · 53 (2, 4) A x 4 + x 2 + 637 (2, 2) 3 (2, 2, 4)<br />
−2072 −7 · 8 · 37 (2, 8) B x 4 + 34x 2 − 7 (2, 2) ≥ 3 (2, 2, 8)<br />
−2379 −3 · 13 · 61 (4, 4) ≥ 3 (4, 4, 8)<br />
−2392 −23 · 8 · 13 (2, 4) B x 4 + 18x 2 − 23 (2) 2 (2, 2, 8)<br />
−1780 have finite (2-)class field tower even though rank Cl2(k 1 ) ≥ 3. Of<br />
course, it would be interesting to determine the length of their towers.<br />
The structure of this paper is as follows: We use results from group theory<br />
developed in Section 2 to pull down the condition rank Cl2(k 1 ) = 2 from the<br />
field k 1 with degree 2 m+2 to a subfield L of k 1 with degree 8. Using the<br />
arithmetic of dihedral fields from Section 4 we then go down to the field K<br />
of degree 4 occurring in Theorem 1.<br />
2. Group Theoretic Preliminaries.<br />
Let G be a group. If x, y ∈ G, then we let [x, y] = x−1y−1xy denote the<br />
commutator of x and y. If A and B are nonempty subsets of G, then [A, B]<br />
denotes the subgroup of G generated by the set {[a, b] : a ∈ A, b ∈ B}.<br />
The lower central series {Gj} of G is defined inductively by: G1 = G and<br />
Gj+1 = [G, Gj] for j ≥ 1. The derived series {G (n) } is defined inductively<br />
by: G (0) = G and G (n+1) = [G (n) , G (n) ] for n ≥ 0. Notice that G (1) = G2 =<br />
[G, G] the commutator subgroup, G ′ , of G.<br />
Throughout this section, we assume that G is a finite, nonmetacyclic,<br />
2-group such that its abelianization Gab = G/G ′ is of type (2, 2m ) for some<br />
positive integer m (necessarily ≥ 2). Let G = 〈a, b〉, where a 2 ≡ b 2m<br />
1 mod G2 (actually mod G3 since G is nonmetacyclic, cf. [1]); c2 = [a, b]<br />
and cj+1 = [b, cj] for j ≥ 2.<br />
Lemma 1. Let G be as above (but not necessarily metabelian). Suppose that<br />
d(G ′ ) = n where d(G ′ ) denotes the minimal number of generators of the<br />
derived group G ′ = G2 of G. Then<br />
G ′ = 〈c2, c3, . . . , cn+1〉;<br />
≡