Download - Coordinates

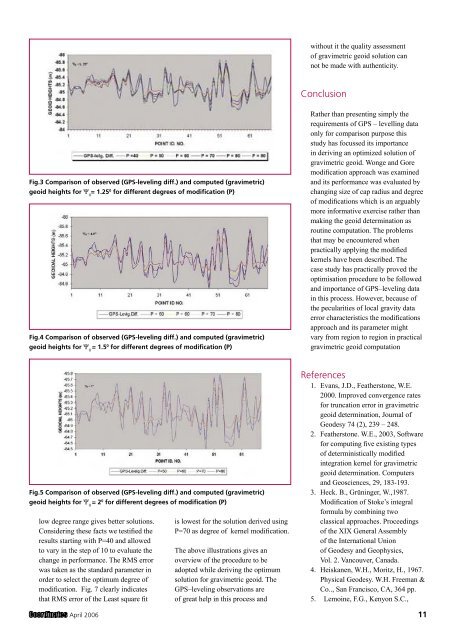
Fig.3 Comparison of observed (GPS-leveling diff.) and computed (gravimetric)
geoid heights for Ψ 0 = 1.25 0 for different degrees of modification (P)
Fig.4 Comparison of observed (GPS-leveling diff.) and computed (gravimetric)
geoid heights for Ψ 0 = 1.5 0 for different degrees of modification (P)
Fig.5 Comparison of observed (GPS-leveling diff.) and computed (gravimetric)
geoid heights for Ψ 0 = 2 0 for different degrees of modification (P)
low degree range gives better solutions.
Considering these facts we testified the
results starting with P=40 and allowed
to vary in the step of 10 to evaluate the
change in performance. The RMS error
was taken as the standard parameter in
order to select the optimum degree of
modification. Fig. 7 clearly indicates
that RMS error of the Least square fit
is lowest for the solution derived using
P=70 as degree of kernel modification.
The above illustrations gives an
overview of the procedure to be
adopted while deriving the optimum
solution for gravimetric geoid. The
GPS–leveling observations are
of great help in this process and
without it the quality assessment
of gravimetric geoid solution can
not be made with authenticity.
Conclusion
Rather than presenting simply the
requirements of GPS – levelling data
only for comparison purpose this
study has focussed its importance
in deriving an optimized solution of
gravimetric geoid. Wonge and Gore
modification approach was examined
and its performance was evaluated by
changing size of cap radius and degree
of modifications which is an arguably
more informative exercise rather than
making the geoid determination as
routine computation. The problems
that may be encountered when
practically applying the modified
kernels have been described. The
case study has practically proved the
optimisation procedure to be followed
and importance of GPS–leveling data
in this process. However, because of
the pecularities of local gravity data
error characteristics the modifications
approach and its parameter might
vary from region to region in practical
gravimetric geoid computation
References
1. Evans, J.D., Featherstone, W.E.
2000. Improved convergence rates
for truncation error in gravimetric
geoid determination, Journal of
Geodesy 74 (2), 239 – 248.
2. Featherstone. W.E., 2003, Software
for computing five existing types
of deterministically modified
integration kernel for gravimetric
geoid determination. Computers
and Geosciences, 29, 183-193.
3. Heck. B., Grüninger, W.,1987.
Modification of Stoke’s integral
formula by combining two
classical approaches. Proceedings
of the XIX General Assembly
of the International Union
of Geodesy and Geophysics,
Vol. 2. Vancouver, Canada.
4. Heiskanen, W.H., Moritz, H., 1967.
Physical Geodesy. W.H. Freeman &
Co.., San Francisco, CA, 364 pp.
5. Lemoine, F.G., Kenyon S.C.,
April 2006 11