Chapter 9 - XYZ Custom Plus

More documents

Recommendations

Info

Chapter Pretest The pretest below contains problems that are representative of the problems you will find in the chapter. Simplify. 1. 4a 2 1 2 5a 1 8 2. 2(5y 2 6) 1 4y Solve each equation. 3. a 1 4 5 22 4. 5y 1 9 2 4y 5 27 1 11 5. 1 } 5 x 5 3 6. 22x 1 9 5 11 7. 2a 1 1 5 5(a 2 2) 2 1 8. x } 3 2 x } 4 5 5 9. Find the value of 3x 2 4 when x 5 22. 10. Is x 5 5 a solution to the equation 6x 2 28 5 1? 11. The sum of a number and 6 is 217. Find the number. 12. If four times a number is decreased by 7, the result is 25. Find the number. 13. Plot the following points: (3, 1), (23, 0), (2, 21), (22, 22). −5−4−3−2−1 −1 −2 −3 −4 −5 y 5 4 3 2 1 1 2 3 4 5 x 14. Graph y 5 3x 2 1. −5−4−3−2−1 −1 −2 −3 −4 −5 y 5 4 3 2 1 1 2 3 4 5 x Getting Ready for Chapter 9 The problems below review material covered previously that you need to know in order to be successful in Chapter 9. If you have any difficulty with the problems here, you need to go back and review before going on to Chapter 9. Simplify. 1. 22 1 7 2. 180 2 45 3. 22 1 (24) 4. 5 } 8 1 3 } 4 5. (24)(5) 6. 6 } 23 7. 3 } 2 (12) 8. 1 2 5 } 4 21 2 4 } 5 2 9. 1 2 5 } 4 21 8 } 15 2 10. 24(21) 1 9 11. 1 } 3 (15) 1 2 12. 5 } 9 (95 2 32) 13. 3x 1 7x 14. 24(3x ) 15. 4(x 2 5) 16. 2 1 1 }2 x 2 17. Write in symbols: the sum of x and 2. 18. Find the perimeter. 3x x 510 Chapter 9 Solving Equations and Inequalities
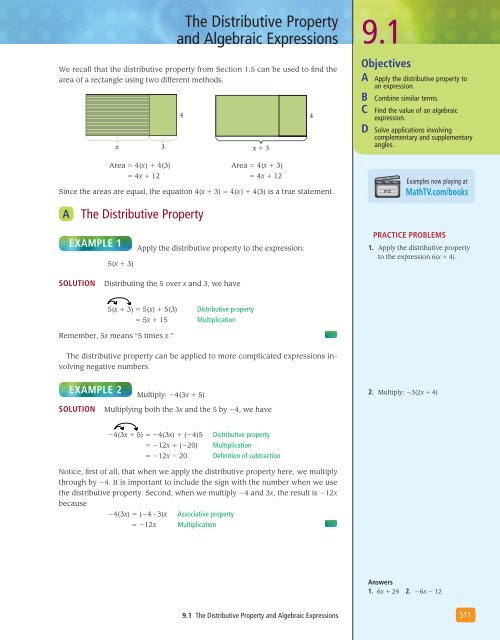
The Distributive Property and Algebraic Expressions We recall that the distributive property from Section 1.5 can be used to find the area of a rectangle using two different methods. x 3 4 x 3 Area 5 4(x ) 1 4(3) Area 5 4(x 1 3) 5 4x 1 12 5 4x 1 12 Since the areas are equal, the equation 4(x 1 3) 5 4(x ) 1 4(3) is a true statement. 4 9.1 Objectives A Apply the distributive property to an expression. B Combine similar terms. C Find the value of an algebraic expression. D Solve applications involving complementary and supplementary angles. Examples now playing at MathTV.com/books A The Distributive Property Example 1 Apply the distributive property to the expression: 5(x 1 3) Practice Problems 1. Apply the distributive property to the expression 6(x 1 4). Solution Distributing the 5 over x and 3, we have 5(x 1 3) 5 5(x) 1 5(3) Distributive property 5 5x 1 15 Multiplication Remember, 5x means “5 times x.” The distributive property can be applied to more complicated expressions involving negative numbers. Example 2 Multiply: 24(3x 1 5) 2. Multiply: 23(2x 1 4) Solution Multiplying both the 3x and the 5 by 24, we have 24(3x 1 5) 5 24(3x) 1 (24)5 Distributive property 5 212x 1 (220) Multiplication 5 212x 2 20 Definition of subtraction Notice, first of all, that when we apply the distributive property here, we multiply through by 24. It is important to include the sign with the number when we use the distributive property. Second, when we multiply 24 and 3x, the result is 212x because 24(3x) 5 (24 ? 3)x Associative property 5 212x Multiplication Answers 1. 6x 1 24 2. 26x 2 12 9.1 The Distributive Property and Algebraic Expressions 511
Page 1: Solving Equations and Inequalities
Page 5 and 6: 9.1 The Distributive Property and A
Page 7 and 8: 9.1 The Distributive Property and A
Page 9 and 10: 9.1 Problem Set 517 Problem Set 9.1
Page 11 and 12: 9.1 Problem Set 519 Find the value
Page 13 and 14: 9.1 Problem Set 521 91. Temperature
Page 15 and 16: Introduction . . . The Addition Pro
Page 17 and 18: 9.2 The Addition Property of Equali
Page 21 and 22: 9.2 Problem Set 529 Applying the Co
Page 23 and 24: The Multiplication Property of Equa
Page 25 and 26: 9.3 The Multiplication Property of
Page 29 and 30: 9.3 Problem Set 537 Find the value
Page 31 and 32: Introduction . . . Linear Equations
Page 33 and 34: 9.4 Linear Equations in One Variabl
Page 37 and 38: 9.4 Problem Set 545 C Applying the
Page 39 and 40: Introduction . . . Applications As
Page 41 and 42: 9.5 Applications 549 Step 2 Assign
Page 43 and 44: 9.5 Applications 551 Example 4 The
Page 45 and 46: 9.5 Applications 553 Step 2 Assign
Page 49 and 50: 9.5 Problem Set 557 Coin Problems 3
Page 51 and 52: Introduction . . . Evaluating Formu
Page 53 and 54:
9.6 Evaluating Formulas 561 The rat
Page 55 and 56:
9.6 Problem Set 563 Problem Set 9.6
Page 57 and 58:
9.6 Problem Set 565 B Maximum Heart
Page 59 and 60:
9.6 Problem Set 567 Applying the Co
Page 61 and 62:
Chapter 9 Summary Combining Similar
Page 63 and 64:
Chapter 9 Review Simplify the expre
Page 65 and 66:
Chapter 9 Cumulative Review 573 28.
Page 67 and 68:
Chapter 9 Projects Solving Equation
show all

Chapter 9 - XYZ Custom Plus

You also want an ePaper? Increase the reach of your titles

Delete template?

Save as template?