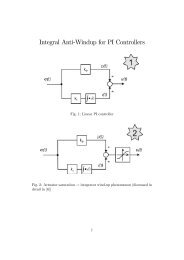
Space Vector Modulated – Direct Torque Controlled (DTC – SVM ...

2. Voltage Source Inverter Fed Induction Motor Drive
range between this point and six-step mode is called overmodulation. This part of the
modulation techniques is not so important in vector controlled drives methods for the
sake of big distortion current and torque. For example, the overmodulation can be
applied in drives working in open loop control mode to increase the value of inverter
output voltage.
The overmodulation has been widely discussed in the literature [16, 33, 55, 75, 89].
Some of methods are proposed as extensions of the carrier based modulation and others
as extensions of space vector modulation. In the carrier based methods overmodulation
algorithm is realized by increasing reference voltage beyond the amplitude of the
triangular carrier signal. In this case some switching cycles are omitted and each phase
is clamped to one of the dc busses.
The overmodulation region for space vector modulation is shown in Fig. 2.20. The
maximum length of vector U c possible to realization in whole range of α angle is equal
3
3
U dc
. It is a radius of the circle inscribed of the hexagon. This value corresponds to
the modulation index equal to 0.907 (see equation 2.26). To realize higher values a
voltage overmodulation algorithm has to be applied. At the end of the overmodulation
region is a six-step mode (at M = 1).
U 3
(010)
U 2
(110)
Six-step mode
M = 1
U 4
(011)
U 0
(000) U 1
(100)
U 7
(111)
(t 2
/T s
)U 2
α
(t 1
/T s
)U 1
U c
Overmodulation range
0.907 < M < 1
Linear range
M ≤ 0.907
U 5
(001) U 6
(101)
Fig. 2.20. Definition of the overmodulation range
32