2003-01-18 - Division of Solid Mechanics

Avd Hållfasthetslära, IKP, Linköpings Universitet
Tentamen TMHL61
Tentamen i Skademekanik och livslängdsanalys TMHL61
lördagen den 18/1 2003, kl 14-18
Solid Mechanics, IKP, Linköping University
Examination in Damage Mechanics and Life Analysis TMHL61
Saturday, January 18, 2003, time: 14-18
Teacher: Tore Dahlberg, 013-28 1116, or 070-66 511 03.
Examination
Part I
Part II
Part I (yellow papers): No books or other external facilities are allowed.
The questions should be answered directly on the yellow papers.
After having handed in Part I (the four yellow papers), Part II (white
papers) is received. The following literature may then be used:
Literature 1. T Dahlberg and A Ekberg: Failure, Fracture, Fatigue - An
Part II Introduction, or T Dahlberg and A Ekberg: Fatigue and Fracture
Design, LiTH-IKP-S-493
2. Sundström B: Handbok och formelsamling i hållfasthetslära, KTH,
1998 (or G Hedner (ed): KTH Formelsamling i Hållfasthetslära) and/or
extractions from these handbooks (for English-speaking students).
3. Handbooks and mathematical tables, dictionaries, glossary.
4. Any small, handhold calculator in one single unit and without any
external communication (as printer, tape-recorder or others).
In the literature minor notations "in the margin" are allowed, but no
problems, solutions, or answers to problems are allowed.
Language
Solutions
Results
Student’s
inspection
Marks/grades
Solutions can be given in Swedish or English.
Solutions will be posted on the notice-board of Solid Mechanics
(Hållfasthetsläras), entrance 15 or 17, corridor B, at 18.00. Solutions
will be available also on the web at http://www.solid.ikp.liu.se, under
the heading "Examinations".
Examination results will be posted on the same notice-board not later
that January 30, 2003.
The correction of the examination papers is open for inspection until
February 28, 2003. After this date the exams are distributed to the
students.
To obtain a mark (grade), the examination and the laboratory work
should be passed
Points 0 to 5 6 to 8 9 to 11 12 to 16
Mark failed 3 4 5
NOTE! This page need not be handed in. Keep it to remember the dates and information given.
Tore Dahlberg, Hållfasthetslära, tel 013-28 1116 2003-01-23

Examination in Damage Mechanics and Life Analysis (TMHL61)
LiTH 2003-01-18
Part 1
1. (1 point)
When working with tensor notations, the Kronecker delta, δ ij , is often very useful.
Explain the use and meaning of this symbol.
Solution and answer here:
The symbol δ ij is defined as a tensor with the following property:
δ ij = ⎧ 0 if i ≠ j
⎨
1 if i = j
Indexes i and j stand for the three coordinate directions (x, y, z) or (r, Θ, z) or (1, 2, 3)
and so on.
2. (1 point)
Explain the phenomenon plastic instability.
Solution and answer here:
When a bar is loaded so that yielding occurs, it will be more narrow (cross-sectional
area will decrease), and, due to the plastic deformation, there will be plastic hardening
(deformation hardening) of the material. When loading the bar, plastic instability occurs
when the deformation hardening ("increase of yield limit") can not compensate for the
area reduction of the cross section.
6 2003-01-23/TD

Examination in Damage Mechanics and Life Analysis (TMHL61)
LiTH 2003-01-18
Part 1
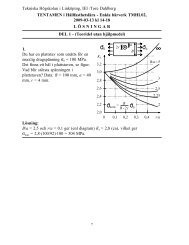
3. (1 point) Constant-amplitude fatigue strengths for materials
subjected to different cyclic loading conditions are
often expressed in Haigh diagrams. Consider the five
a
loading cases where the loading varies sinusoidally
A
and
1. the mean value σ m is constant,
200
100
B 2. the amplitude σ a is constant,
3. the maximum value σ max (= σ m + σ a ) is constant,
0
0
m
100 200 300 400 MPa
4. the minimum value σ min (= σ m − σ a ) is constant,
and
5. the stress ratio R = σ min /σ max is constant.
In the Haigh diagram given, two straight lines (A
and B) are shown. For each line one of the five
loading conditions applies.
(a) Determine which one of the five loading variables is constant for line A shown in
the figure (i.e., match line A to one of the five loading conditions). Explain your choice.
(b) Determine which one of the five loading variables is constant for line B shown in
the figure (i.e., match line B to one of the five loading conditions). Explain your choice.
Solution and answer here:
For line A one notices that σ m + σ a is a constant (= 300 MPa). Thus, line A gives that
stress σ max is constant.
For line B one notices that σ m − σ a = σ min is constant (= 200 MPa). Thus, stress σ min is
constant.
Answer:
(a) Line A: stress σ max is constant, (b) line B: stress σ min is constant.
4. (1 point)
To determine the fatigue limit of a material, the so-called stair-case method is
sometimes used. Explain the principles, requirements and assumptions of this method
(no formulas are needed).
Solution and answer here:
The fatigue testing is performed so that if a test specimen fails (due to fatigue), the next
specimen will be tested at a lower stress level. If it does not fail (becomes a run-out),
the next specimen will be tested at a higher stress lever. Then, assuming that the yield
limit has a normal distribution, and knowing the number of failures and run-outs at each
stress level, the mean value and the standard deviation of the fatigue limit can be
estimated. This requires that tests performed at a stress level too far away from the
mean value should be rejected.
7 2003-01-23/TD

5. (3 points)
( ) 0
Examination in Damage Mechanics and Life Analysis (TMHL61)
LiTH 2003-01-18
y
2 a
2 W
P
x
Part 2
A large thin plate contains a through-thickness crack
with initial crack length 2a 0 = 15 mm. The plate is
loaded by a force P. Upon loading the plate,
symmetric stable crack growth was observed. At load
P = 300 kN the plate fractured. During the loading
the crack opening δ(0) was recorded, and just prior to
the fracture, the crack opening displacement was
found to be δ(0) = 0.1 mm.
Use the Dugdale model to determine the crack length
just before the plate fractured.
P
Numerical data: Modulus of elasticity E = 210 GPa, yield strength σ Y = 480 MPa, plate
width 2W = 0.4 m and plate thickness t = 0.002 m (i.e. the plate is so thin that the
conditions at the crack tip may be regarded as plane stress).
Solution:
The load P = 300 kN gives stress σ ∞ = P/2Wt = 375 MPa in the plate.
Since plane stress is at hand, the Dugdale model may be used. It gives
δ(0) = 8 σ Y a 1 + sin(πσ
E π
ln⎧ ∞ /2σ Y ) ⎫
⎨
cos(πσ ∞ /2σ Y )
Enter the given numerical values and solve for the unknown crack (half-)length a = a crit .
One then obtains
a crit
= δ(0) E π ⎛ ⎜⎝ ln 1 + sin(πσ ∞/2σ Y ) ⎞
⎟
8 σ Y cos(πσ ∞ /2σ Y ) ⎠
− 1
210 000 ⋅ π ⎛ 1 + sin(π ⋅ 375/2 ⋅ 480) ⎞
= 0, 0001 ⎜ln ⎟ = 0, 0098 m
8 ⋅ 480 ⎝ cos(π ⋅ 375/2 ⋅ 480) ⎠
Thus, the total crack length at failure is 2a crit = 19.6 mm (= 1.31⋅2a 0 ).
− 1
⎬
⎭
8 2003-01-23/TD

6.
2 h
Examination in Damage Mechanics and Life Analysis (TMHL61)
LiTH 2003-01-18
a
a
a
Q
P
P
Q
M
b
2h
2h
b
Part 2
Determine, by use of superposition of stress intensity
factors, the stress intensity factor K I for the split
beam with a long crack, see figure. The crack length
is a, beam thickness is b and beam height is 2h,
where a >> b and a >> h. The material is linear
elastic with modulus of elasticity E. The beam is
loaded symmetrically with two opposite forces P at
the beam ends. The sliding boundary condition to
the right is such that the slope of the beam end is
always zero. Assume plane stress conditions.
The following results, taken from Problems 5/2 and
5/3 in the textbook can be used:
Double cantilever beam with stress intensity factor
K I = 2 Qa / bh
Double cantilever beam with energy release rate G =
12M 2 / Eb 2 h 3
Solution:
First, remove the boundary condition to the right and add a bending moment M at the
beam end. The bending moment M should be such that the slope at the free end of the
cantilever beam is zero. One obtains, for slope Θ,
a
Q
M
M
√⎺3
which gives M = Qa / 2, and here Q = P
Problem 5/3 gives, for plane stress, that K M I = = 2 M / bh
Now superposition can be used to calculate the stress intensity factor in the case asked
for. One obtains, using M = Qa / 2 and Q = P,
K I = K I Q − K I M = 2 √⎺3 Qa
bh√⎺h
√⎺h
Θ = Q a 2
2EI − M a = 0
EI
√⎺⎺⎺EG √⎺3 √⎺h
− 2 √⎺3 M
bh√⎺h = 2 √⎺3 Qa
bh√⎺h
− 2 √⎺3 Qa
2bh√⎺h = √⎺ 3 Qa
bh√⎺h = √⎺ 3 Pa
bh√⎺h
9 2003-01-23/TD

Examination in Damage Mechanics and Life Analysis (TMHL61)
LiTH 2003-01-18
7. (3 points) One type of test specimen to determine the
p
fracture toughness of a material is the double
cantilever beam, see figure. The height is 2h
= 30 mm (the width t is large).
At plane strain, the stress intensity factor can
2 h be written
p
a
where ν is the Poisson ratio, ν = 0.3, and p is
the loading per unit of the width of the test
specimen.
Paris’ law for the material reads da
dN = 5.1 × 10 − 12 (∆ K I ) 3
m per cycle
where ∆K I has the unit MPa m 1/2 .
The fracture toughness of the material is (in this example) determined in the following
way: First a crack of length a 0 = 20 mm is created by machining. Then, to obtain a
sharp crack tip, the test specimen is subjected to a loading p such that the load p is
cycled between 0 och 0.9 MN/m. This is done for N = 15 000 cycles. When this is done
the cyclic loading is stopped.
(a) Calculate the crack length a final obtained by the cyclic loading.
After this, the test specimen is loaded by a static, monotonically increasing load p until
fracture occurs. One obtains the final fracture of the specimen at load p = 1.8 MN/m.
(b) Determine the fracture toughness of the material.
The yield limit of the material is σ s = σ Y = 1000 MPa.
Solution: (a) First determine the crack length after the cyclic loading. Paris’ law gives
Which gives
da
dN = 5.1 × 10 ⎛ 3
− 12 2√⎺3 0.9 a ⎞
⎜ ⎟⎠ ⎝ 0.91 0.015 3 / 2
1 ⎧
− 2
from which is solved a final = 25.754 mm.
(b) At the final, monotonically increasing loading the critical crack length is a final =
25.754 mm. The fracture toughness is obtained from
K I = K Ic = 2 √⎺3 p failure a final
= 96.06 MPa√⎺m
1 − ν 2 h 3/2
Thus K Ic = 96 MPa m 1/2 .
Here linear elastic fracture mechanics (LEFM) was used. Was it allowed?
One has
2.5 ⎛ 2
K Ic ⎞
⎜ ⎟⎠ = 2.5 ⎛ 2
96 ⎞
⎜ ⎟ = 0.023 m < a ⎝ σ Y ⎝ 1000⎠
final = 0.02575 m
Thus, it was OK to use LEFM for the final failure.
⎨
a final
m per cycle
K I = 2 √⎺3
1 − ν 2 p a
h 3/2
1
− 1 ⎫
⎬
2 2
a = 0.033078 ⋅ N = 496.16 0 ⎭ (1/m2 )
10 2003-01-23/TD

Examination in Damage Mechanics and Life Analysis (TMHL61)
LiTH 2002-10-2
Part 2
8. (3 points)
To determine the fatigue limit of a material a number of experiments were performed
according to the "staircase" method. Calculate an estimation of the mean value and the
standard deviation of the fatigue limit of the material if the following test series were
obtained (stresses in MPa)
σ a = 90, 99, 108, 117, 126, 117, 108, 117, 126, 117, 126, 135, 126, 117, 108, 117, 126,
117, 126, 117, 108, 117 MPa,
where the last test (117 MPa) became a run-out. The fatigue limit is supposed to have a
normal distribution.
Solution:
From the load levels used in the test it is concluded that the test specimens failed
(indicated by an F) or did not fail (became run-outs, indicated by RO) as follows:
σ a = 90(RO), 99(RO), 108(RO), 117(RO), 126(F), 117(F), 108(RO), 117(RO), 126(F),
117(RO), 126(RO), 135(F), 126(F), 117(F), 108(RO), 117(RO), 126(F), 117(RO),
126(F), 117(F), 108(RO), 117(RO) MPa.
The test series seems to have started on a too low stress level. Therefore, from the 22
tests the first three tests are discarded (the first change from run-out to failure came at
stress level 117 MPa). From the remaining 19 tests 10 are run-outs and 9 are failures.
The less frequent event should be analysed. Thus, analyse the failures. The failures
occurred at
σ a = 126(F), 117(F), 126(F), 135(F), 126(F), 117(F), 126(F), 126(F), 117(F) MPa.
These events give the following table (see compendium)
I II III IV V
117 0 3 0 0
126 1 5 5 5
135 2 1 2 4
N = 9 A = 7 B = 9
The mean value of the fatigue limit is estimated to (step d = 9 MPa)
S’ m = S 0 + d ⎧ A
⎨
N − 1 ⎫
⎬
2
= 117 + 9 ⎧ 7
⎨
⎭ 9 − 1 ⎫
⎬ = 120 MPa
2⎭ Further, one obtains
NB − A 2
= 9 ⋅ 9 − 72
= 0.395
N 2 9 2
The standard deviation of the fatigue limit is estimated to
s’ = 1.62d ⎧ NB − A 2
⎨ + 0.029 ⎫ ⎬ = 6.2 MPa
⎭
N 2
11 2003-01-23/TD