2003-01-18 - Division of Solid Mechanics

Examination in Damage Mechanics and Life Analysis (TMHL61)
LiTH 2003-01-18
Part 1
3. (1 point) Constant-amplitude fatigue strengths for materials
subjected to different cyclic loading conditions are
often expressed in Haigh diagrams. Consider the five
a
loading cases where the loading varies sinusoidally
A
and
1. the mean value σ m is constant,
200
100
B 2. the amplitude σ a is constant,
3. the maximum value σ max (= σ m + σ a ) is constant,
0
0
m
100 200 300 400 MPa
4. the minimum value σ min (= σ m − σ a ) is constant,
and
5. the stress ratio R = σ min /σ max is constant.
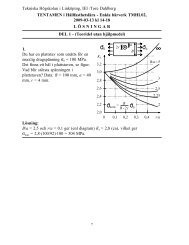
In the Haigh diagram given, two straight lines (A
and B) are shown. For each line one of the five
loading conditions applies.
(a) Determine which one of the five loading variables is constant for line A shown in
the figure (i.e., match line A to one of the five loading conditions). Explain your choice.
(b) Determine which one of the five loading variables is constant for line B shown in
the figure (i.e., match line B to one of the five loading conditions). Explain your choice.
Solution and answer here:
For line A one notices that σ m + σ a is a constant (= 300 MPa). Thus, line A gives that
stress σ max is constant.
For line B one notices that σ m − σ a = σ min is constant (= 200 MPa). Thus, stress σ min is
constant.
Answer:
(a) Line A: stress σ max is constant, (b) line B: stress σ min is constant.
4. (1 point)
To determine the fatigue limit of a material, the so-called stair-case method is
sometimes used. Explain the principles, requirements and assumptions of this method
(no formulas are needed).
Solution and answer here:
The fatigue testing is performed so that if a test specimen fails (due to fatigue), the next
specimen will be tested at a lower stress level. If it does not fail (becomes a run-out),
the next specimen will be tested at a higher stress lever. Then, assuming that the yield
limit has a normal distribution, and knowing the number of failures and run-outs at each
stress level, the mean value and the standard deviation of the fatigue limit can be
estimated. This requires that tests performed at a stress level too far away from the
mean value should be rejected.
7 2003-01-23/TD