Asymptotic Methods in Statistical Inference - Statistics Centre

More documents

Recommendations

Info

80 • An example of a strong CI: 1 ∼ ( 2 ). The CI derived from the 2-sided t-test is ¯ ± 2 √ ,with ¯ − ( ∈ ) = Ã¯¯¯¯¯ √ ¯ ≤ 2 = ³ | −1 | ≤ 2´ → 1 − ; since the probability does not depend on the parameters the convergence is uniform. — The above is typical when the CI is based on a ‘pivot’ — a function of the data and of the parameter whose distribution does not depend on the parameters. ¯ !
81 • Example. 1 ∼ () ( 0); test = 0 . The large-sample test has acceptance ¯ region ¯√ ³ ¯ − 0´ √ 0¯¯¯ ≤ 2 ,equivalently ³ ¯ − 0´2 ≤ 2 2 0 , resulting in the CI with endpoints ¯ + 2 2 2 ± 2 √ v uut ¯ + 2 2 4 (9.1) Replacing √ 0 by √ ¯ in the test statistic leads instead to the CI ¯ ± 2 s ¯ which agrees with the previous one up to terms which are ( −1 ) (i.e. if such terms are dropped). This interval is not strong. Toseethis,notethat ¯ − 2 r ¯ ≤ ≤ ¯ + 2 r ¯ implies that ¯ 0, hence ⎛ s s ⎞ ⎝ ¯ ¯ ¯ − 2 ≤ ≤ ¯ + ⎠ 2 ≤ 1 − ³ ¯ =0´ =1− − → 0as → 0
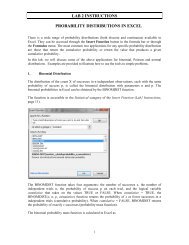
Page 1 and 2:
STATISTICS 665 ASYMPTOTIC METHODS I
Page 3 and 4:
II LARGE-SAMPLE INFERENCE 42 5 Intr
Page 5 and 6:
V LIKELIHOOD METHODS 169 19 Maximum
Page 7 and 8:
Part I PROBABILISTIC PRELIMINARIES
Page 9 and 10:
The ‘rate’ of convergence refer
Page 11 and 12:
11 imagine ‘large’ but remain
Page 13 and 14:
13 • For the ( ) distribution,
Page 15 and 16:
15 —Corollary1: → If h (
Page 17 and 18:
17 2. Slutsky’s Theorem; conseque
Page 19 and 20:
— By the CLT, − q (1 − ) 1
Page 21 and 22:
21 • Corollary 1: If → the
Page 23 and 24:
23 • First an application. Let 2
Page 25 and 26:
25 with d.f. (), then there is a
Page 27 and 28:
27 next lecture), = 1− " ( )+
Page 29 and 30: 29 • CLT via the Edgeworth expans
Page 31 and 32: 31 (why?) with ‘cumulant generati
Page 33 and 34: Thus in (3.2), () () isthec.f.of
Page 35 and 36: 35 • Delta method. Suppose that
Page 37 and 38: 37 • Uniformity—read§2.6 • C
Page 39 and 40: 39 suppose that → 0. Then X =1
Page 41 and 42: 41 • Under this condition ˆ is (
Page 43 and 44: 43 5. Introduction to asymptotic te
Page 45 and 46: 45 • We often work instead with t
Page 47 and 48: 47 • Two-sample problems. Suppose
Page 49 and 50: 49 • Example 2: 1 ∼ P(),
Page 51 and 52: 51 term is Ã √ ˆ ( ( 0 )
Page 53 and 54: 53 • More useful is to study the
Page 55 and 56: 55 • Example: t-test of a mean.
Page 57 and 58: 57 • Efficacy. Test : = 0 vs.
Page 59 and 60: 59 Put = − and test for tre
Page 61 and 62: 61 7. Relative efficiency • Relat
Page 63 and 64: • The constraint (1) ∼ (2)
Page 65 and 66: 65 =1. Theefficacy is = 0 q (0)
Page 67 and 68: 67 • Example 3. In this example
Page 69 and 70: 69 Proof of ‘ 1’: From 1 − (
Page 71 and 72: 71 • We will consider only ‘lev
Page 73 and 74: 73 • Example 1. Suppose we (mista
Page 75 and 76: 75 To see this take 0 = 0 for simp
Page 77 and 78: 77 The numerator of is normally d
Page 79: 79 9. Confidence intervals • X =(
Page 83 and 84: 83 • A strong CI on a population
Page 85 and 86: 85 • A more involved example of a
Page 87 and 88: 87 We exhibit 1 () 2 () → 1−
Page 89 and 90: 10. Point estimation; Asymptotic re
Page 91 and 92: 91 Recall that if 0 () 6= 0 (assum
Page 93 and 94: 93 where (with being a bound on |
Page 95 and 96: • Asymptotic Relative Efficiency.
Page 97 and 98: 97 0.0 0.1 0.2 0.3 0.4 0.5 0.6 -3 -
Page 99 and 100: 99 that then √ ³ ¯ − ´
Page 101 and 102: 101 — This is also the ARE of the
Page 103 and 104: 103 We minimize Z h 2 ()+2 2 ()
Page 105 and 106: 105 In a broad class of cases, comp
Page 107 and 108: 107 The ARE of the estimates consid
Page 109 and 110: 109 We have lim →∞ { ∗ () −
Page 111 and 112: 111 13. Random vectors; multivariat
Page 113 and 114: 113 • X () () → c (constant)
Page 115 and 116: 115 • Multivariate normality. We
Page 117 and 118: 117 • If X ∼ (μ Σ) then an
Page 119 and 120: 119 14. Multivariate applications
Page 121 and 122: 121 One can eliminate the last elem
Page 123 and 124: 123 have = (|)+ ¯ (| ¯) =
Page 125 and 126: 125 at = 1. In this latter case Ã
Page 127 and 128: 127 Proof: Write Then +1 = − X
Page 129 and 130: 129 15. Expectation functionals; U-
Page 131 and 132:
131 • A closely related estimate,
Page 133 and 134:
1≤≤ 133 — e.g. = 2; let =
Page 135 and 136:
135 • Rao-Blackwell Theorem: We c
Page 137 and 138:
137 • Here we get the variance of
Page 139 and 140:
139 16. Asymptotic normality of U-s
Page 141 and 142:
141 Under , ( + ) = () ∼ (0 1)
Page 143 and 144:
143 • Proofofclaim1: [( − ) |
Page 145 and 146:
145 • V-statistics. Recall that i
Page 147 and 148:
147 17. Influence function analysis
Page 149 and 150:
149 By using the fact that | 2 −
Page 151 and 152:
151 — e.g. If ( )= [], then ³
Page 153 and 154:
153 By the CLT and Slutsky’s theo
Page 155 and 156:
But −1 X =1 155 ( ≥ ) =
Page 157 and 158:
157 18. Bootstrapping • Suppose t
Page 159 and 160:
159 • In each of the examples abo
Page 161 and 162:
161 • Example 2. ( )=bias. Writ
Page 163 and 164:
163 • For the measure (18.1) we t
Page 165 and 166:
165 (True for functionals (·) con
Page 167 and 168:
167 • Indeed, since ( ) has plu
Page 169 and 170:
169 Part V LIKELIHOOD METHODS
Page 171 and 172:
171 By this, for large samples and
Page 173 and 174:
173 • Assume: (C1) Identifiabilit
Page 175 and 176:
175 • Under stronger conditions o
Page 177 and 178:
177 Then (here we use only twice; t
Page 179 and 180:
179 • Information Inequality. (Cr
Page 181 and 182:
181 • Example: 1 the indicator
Page 183 and 184:
183 Theorem: Under (C1)-(C7) and th
Page 185 and 186:
185 has a limit distribution, so th
Page 187 and 188:
187 Claim: (i) (ii) (iii) 0 ( 0 )
Page 189 and 190:
189 Define the ‘scores’ ( −
Page 191 and 192:
191 • The MLE is not the only eff
Page 193 and 194:
193 The variance-minimizing choice
Page 195 and 196:
195 • Multiparameter likelihood e
Page 197 and 198:
197 • Efficiency. Under appropria
Page 199 and 200:
199 asymptotic normality of the sam
Page 201 and 202:
201 • Likelihood ratio test. Put
Page 203 and 204:
203 and 000 ( ∗∗ ) is (1)
Page 205 and 206:
205 • Example. 1 ∼ Logistic,
Page 207 and 208:
207 • Multiparameter inferences.
Page 209 and 210:
209 For testing, I( 0 ) is replaced
Page 211 and 212:
211 24. Examples Example: 1 ∼
Page 213 and 214:
213 with and I (θ 0 )= 1 I 11 (θ
Page 215 and 216:
215 • The likelihood ratio statis
Page 217 and 218:
217 • If instead of testing =
Page 219 and 220:
219 The parameter vector is θ = ³
Page 221 and 222:
221 25. Higher order asymptotics
Page 223 and 224:
223 As in Lecture 10, cov h i 2 h
Page 225 and 226:
225 • The normal approximation, a
Page 227 and 228:
227 By uniqueness of m.g.f.s, (;
Page 229 and 230:
229 • Example 2. Let = P 1 w
Page 231:
231 • The error of Saddlepoint
show all

Asymptotic Methods in Statistical Inference - Statistics Centre

You also want an ePaper? Increase the reach of your titles

Delete template?

Save as template?