DoD MS Human Capital Strategy 20101202 - Modeling & Simulation ...

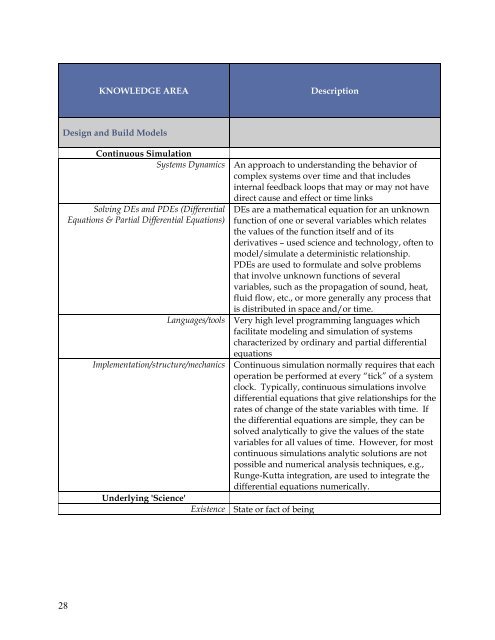
KNOWLEDGE AREA
Description
Design and Build Models
Continuous Simulation
Systems Dynamics An approach to understanding the behavior of
complex systems over time and that includes
internal feedback loops that may or may not have
direct cause and effect or time links
Solving DEs and PDEs (Differential DEs are a mathematical equation for an unknown
Equations & Partial Differential Equations) function of one or several variables which relates
the values of the function itself and of its
derivatives – used science and technology, often to
model/simulate a deterministic relationship.
PDEs are used to formulate and solve problems
that involve unknown functions of several
variables, such as the propagation of sound, heat,
fluid flow, etc., or more generally any process that
is distributed in space and/or time.
Languages/tools Very high level programming languages which
facilitate modeling and simulation of systems
characterized by ordinary and partial differential
equations
Implementation/structure/mechanics Continuous simulation normally requires that each
operation be performed at every “tick” of a system
clock. Typically, continuous simulations involve
differential equations that give relationships for the
rates of change of the state variables with time. If
the differential equations are simple, they can be
solved analytically to give the values of the state
variables for all values of time. However, for most
continuous simulations analytic solutions are not
possible and numerical analysis techniques, e.g.,
Runge-Kutta integration, are used to integrate the
differential equations numerically.
Underlying 'Science'
Existence State or fact of being
28