Pit Pattern Classification in Colonoscopy using Wavelets - WaveLab

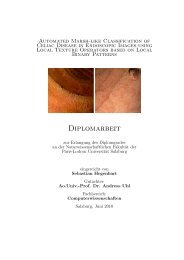
4 Automated pit pattern classification
(a) Perfect
(b) Noisy
Figure 4.5: Distance matrices for the two-class case
calculated. The class which is assigned to the image to classify is the one which has the centroid
with the smallest distance to the input image according to the respective decomposition
trees.
4.3.5 Centroid classification based on BB and LDB (CCLDB)
Like the previous method, this method does not use any wavelet based features too, although,
in contrast to the previous method, it is based on the best-basis algorithm and the
LDB algorithm. This approach uses the BB and the LDB just for the creation of wavelet
decomposition trees.
First of all the LDB is calculated for the training images which results in a LDB tree T LDB .
Then, using the best-basis algorithm, the decomposition trees T i for all training images
based on some cost function are calculated. Based on these decomposition information, for
each training image I i a distance vector D i is calculated:
D i = dv(T i , T LDB ) (4.61)
where dv is a function, which returns a vector containing all subband ids which are not equal
among the two trees passed as arguments. In other words the distance vector contains all
subband ids which are present either in T i or T LDB but not in both trees. Thus the distance
vectors represent the differences between the LDB tree and the trees for the images in terms
of the tree structure.
Then, based on the distance vectors of the images, a distance matrix D can be calculated.
The matrix D is similar to the one described in section 4.3.4, but the matrix now contains
the euclidean distances between the difference vectors instead of the distances between the
56