Computer (matrix) version of the stiffness method 1. The computer ...
Computer (matrix) version of the stiffness method 1. The computer ...
Computer (matrix) version of the stiffness method 1. The computer ...
Create successful ePaper yourself
Turn your PDF publications into a flip-book with our unique Google optimized e-Paper software.
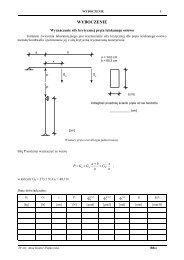
<strong>The</strong> frame consists <strong>of</strong> four beam elements which are interconnected in five nodes. <strong>The</strong> element<br />
<strong>stiffness</strong> matrices and vectors <strong>of</strong> nodal reactions due to <strong>the</strong> span loading are found in <strong>the</strong> local coordinates<br />
for each element<br />
1 2 1 1<br />
1<br />
1<br />
1<br />
x ~<br />
2<br />
y ~ x ~<br />
3<br />
y ~<br />
4<br />
y ~ x ~<br />
y ~ x ~<br />
2<br />
2<br />
are transformed to <strong>the</strong> global co-ordinates<br />
1 2 2 3<br />
1 x<br />
2<br />
y<br />
y<br />
and <strong>the</strong>y can be represented as<br />
x<br />
⎡K11,1<br />
K12,1<br />
⎤ ⎡K11,2<br />
K12,2<br />
⎤ ⎡K11,3<br />
K12,3<br />
⎤ ⎡K11,3<br />
K12,3<br />
⎤<br />
K 1 = ⎢ ⎥ K 2 = ⎢<br />
⎥ K 3 = ⎢<br />
⎥ K 1 = ⎢<br />
⎥<br />
⎣K<br />
21,1 K22,1⎦<br />
⎣K<br />
21,2 K22,2<br />
⎦ ⎣K<br />
21,3 K22,3<br />
⎦ ⎣K<br />
21,3 K22,3<br />
⎦<br />
Note, that <strong>the</strong> local element numbers <strong>of</strong> element nodes can be replaced with <strong>the</strong> global numbers:<br />
Element 1: 1 – 1, 2 – 2, element 2: 1 – 2, 2 – 3, element 3: 1 – 2, 2 – 4, element 4: 1 – 3, 2 – 5.<br />
<strong>The</strong>se relations enable a proper “addressing” <strong>of</strong> <strong>the</strong> subsequent submatrices <strong>of</strong> <strong>the</strong> element<br />
<strong>stiffness</strong> matrices K e in <strong>the</strong> global <strong>stiffness</strong> <strong>matrix</strong> <strong>of</strong> <strong>the</strong> frame K. <strong>The</strong> assembly scheme is<br />
2<br />
4<br />
3<br />
y<br />
x<br />
3<br />
y<br />
4<br />
5<br />
x<br />
K =<br />
K 11,1 K 12,1<br />
K 21,1<br />
K 22,1+K 11,2+<br />
+K 11,3<br />
K 12,2<br />
K 12,3<br />
K 21,2 K 22,2 +K 11,4 K 12,4<br />
K 22,3<br />
K 21,3<br />
K 21,4 K 22,4<br />
Note, that in this scheme each box corresponds to a node and it represents 3×3 elements <strong>of</strong> <strong>the</strong><br />
global <strong>stiffness</strong> <strong>matrix</strong> corresponding to three displacements at <strong>the</strong> given node.<br />
Let us also consider <strong>the</strong> assembly <strong>of</strong> <strong>the</strong> global force vector P.<br />
Out <strong>of</strong> four beams constituting <strong>the</strong> frame only one – No. 4 has a span loading and consequently<br />
<strong>the</strong> non-zero vector <strong>of</strong> reactions due to <strong>the</strong> loading. <strong>The</strong>se vectors for <strong>the</strong> o<strong>the</strong>r beams are zero:<br />
~ ~ ~<br />
R R = R = R = R = R = 0<br />
01 = 02 03 01 02 03<br />
To calculate <strong>the</strong> vector for <strong>the</strong> fourth element <strong>the</strong> loading can be split into uniformly distributed load<br />
acting along <strong>the</strong> beam and transverse to <strong>the</strong> beam<br />
q<br />
q 1 l<br />
q 2<br />
2 l<br />
2<br />
12<br />
q q 2 l<br />
1 = qsinϕcosϕ<br />
q 2 qcos 2 ϕ<br />
l<br />
=<br />
+ 2<br />
l<br />
ϕ<br />
l 2 l<br />
q 1 l<br />
2 2<br />
2 l<br />
2<br />
12