Computer (matrix) version of the stiffness method 1. The computer ...

Computer (matrix) version of the stiffness method
1. The computer version of the stiffness matrix is a generalization of the classical version leading
towards the computer applications and the finite element method. The basic ideas remain the
same, though some assumptions are released.
The computer version is based on the following assumptions
– displacements and strains remain small compared to the dimensions of the structure – the
equilibrium is related to the undeformed configuration (1 st order theory)
– material is linearly elastic with classical Hooke’s law
– plane cross-sections remain plane during bending
– from these three conditions it follows that the superposition rule is valid
Compared to the classical approach the assumption of no deformability in the axial direction of the
bars is released. Hence, the influence of the axial forces on the displacements is taken into
account.
The main concept of the method remains, i.e. the bar structure is subdivided (discretised) into a
finite number of bars (elements). The ends of the elements are called nodes.
Truss
i
e
k
Frame
e – element number
i, k – node numbers
The deformed state of the structure is described by the generalized nodal displacements, i.e. linear
displacements and angles of cross-section rotations. Type and number of generalized
displacements in the node depends on the type of structure. The nodal displacements are also
called the nodal degrees of freedom. They can be assembled into a vector of nodal displacements
q n , those for the element – into the vector of element displacements q e and, finally, those for the
entire structure – into the global vector of displacements q.
Plane truss
y
x
i
u i
q
n
⎡ui
⎤
= ⎢ ⎥
⎣v
i ⎦
v i
z
3D truss
y
u i
i
w i
v i
x
q
n
⎡ui
⎢
=
⎢
v i
⎢⎣
wi
⎤
⎥
⎥
⎥⎦

Plane frame
x
i
v i
u i
q
n
⎡ui
⎤
⎢ ⎥
=
⎢
v i ⎥
⎢⎣
ϕ ⎥
i ⎦
y
x
z
3D frame
y
u i
ϕ x
ϕ z
ϕ i
i
w i
v i
ϕ x
ϕ y
Plane yz
q
n
⎡ui
⎤
⎢ ⎥
⎢
v i ⎥
⎢w
⎥
i
= ⎢ ⎥
⎢ϕ
x ⎥
⎢ϕ
⎥
y
⎢ ⎥
⎢⎣
ϕz
⎥⎦
Interpretation
of the rotation angle
The displacements presented in the above figures are referred to the global sets of co-ordinates xy
or xyz. In practice it is much easier to form the basic equations on the level of elements, hence, the
local systems of co-ordinates are introduced. The values corresponding to the local co-ordinates
are additionally denoted with tildes.
The slope-defection formulae from the classical stiffness method are replaced by the element
stiffness matrix, which relates the element displacements in local co-ordinates to the reactions at
the element supports in local co-ordinates:
~ K
~ ~
Re
= Keq
~
e e
[ k eij
]
n×
n
where n is the number of element degrees of freedom. The elements of the stiffness matrix
represent reactions at the element supports created by unit displacements. For instance, the
element k ~ eij represents the reaction number i created by the action of the displacement q
~ = j 1
First, let us consider the plane truss element. In this case the vectors of element displacements
and reactions have four components
= ~
~ q
~
i
R 1,
1
2
~ R 3,
q
~
3
x ~
k
e
~ ~
l
R 4,
q 4
~ R
~
2,
q
y ~
q
~
e
⎡u
~ ⎤ ⎡ ~
i q1
⎤
⎢ ⎥ ⎢ ⎥
⎢v
~ ~
i ⎥ = ⎢q2
= ⎥
⎢u
~ ⎥ ⎢~
⎥
k q3
⎢ ⎥ ⎢~
⎥
~
⎣v
k
⎦ ⎢⎣
q4
⎥⎦
~
R
e
⎡ ~
R
⎢ ~
⎢R
=
⎢ ~
R
⎢ ~
⎢⎣
R
1
2
3
4
⎤ ⎡−
Ni
⎤
⎥ ⎢ ⎥
⎥ ⎢
−Ti
= ⎥
⎥ ⎢ N ⎥
k
⎥ ⎢ ⎥
⎥⎦
⎣ Tk
⎦

N
State q ~
1
1 =
e
i
q ~
y ~
1 =
1
k
N
x ~
From the Hooke’s law
EA ~ EA ~
N = − ⋅1
⇒ R1
= , R3
l
l
EA
= −
l
State q ~
1
i
N
3 =
e
k
N
q ~
3 = 1
x ~
From the Hooke’s law
EA ~ EA ~ EA
N = ⋅1
⇒ R1
= − , R3
=
l
l l
y ~
State
~
1
i
q y ~ x ~
2 =
e
k
x ~
No internal forces are created. The same
situation occurs in the state q ~
1 .
4 =
q ~
2 =
1
y ~
Summarising of these results yields the following element stiffness matrix
~
K
e
⎡ 1
⎢
EA ⎢
0
=
l ⎢−1
⎢
⎣ 0
From the physical interpretation of the element stiffness matrix it follows, that for instance the first
column of this matrix represents the vector of reactions in the element created by the action of the
displacement q ~
1 .
1 =
Now, let us consider the stiffness matrix for the plane bar element under bending (i.e. the plane
beam element).
~ R 4,
q
~
4
k
⎡u
~ ⎤ ⎡q
~ ⎤ ⎡ ~
i 1 R ⎤ ⎡−
N ⎤
1
ik
e
~ ⎢ ~ ⎥ ⎢~
⎥ ⎢ ~ ⎥ ⎢ ⎥
R
⎢v
i ⎥ ⎢q2
⎥ ⎢R
⎥ ⎢
−T
6,
q
~
6
2 ik ⎥
~ ⎢ ~ ⎥ ⎢~
~ ϕ q ⎥ ⎢ ~
R
i
⎥ ⎢
i 3
M ⎥
1,
q
~
l
1
~ ~ R3
ik
R q e = ⎢~
⎥ = ⎢~
⎥ R e = ⎢ ⎥ = ⎢ ⎥
5,
q
~
5
~
⎢uk
⎥ ⎢q4
⎥ ⎢R
⎥ ⎢ N
4 ki ⎥
~ ⎢v
~ ⎥ ⎢q
~ ⎥ ⎢ ~
~
⎥ ⎢ ⎥
k 5
Tki
⎢ ⎥ ⎢
~
⎥ ⎢
R5
~ R 2,
q 2
⎥
⎢
~
~ ⎢ ⎥
R 3,
q
~
3
⎣ϕ
k ⎥⎦
⎢⎣
q6
⎥⎦
⎢⎣
R ⎥⎦
⎢⎣
M
6 ki ⎥⎦
0
0
0
0
−1
0
1
0
0⎤
⎥
0
⎥
0⎥
⎥
0⎦

Reactions number 1 and 4 created by the action of displacements number 1 and 4 are obtained in
the same way as in the case of the plane truss element. Note, that these displacements do not
yield any other reactions. Also, these reactions are zero under the action of all the other
displacements. Hence, in the classical plane beam element the action of axial forces and
displacements is fully decoupled from the combined action of shear and bending. The reactions
due to the transverse displacements and cross-section rotations can be found using the slopedeflection
formulae from the classical stiffness method. This yields:
~
R
3
~
R
6
~
R
2
~
R
5
2EI
= M =
ψ
l
2EI
⎛
l ⎝
6EI
4EI
l
6EI
5 2
( 2ϕ
)
~ ~
~ ~ ~ ~
i + ϕk
− 3 ik = ⎜2q3
+ q6
− 3 ⎟ = q2
+ q3
− q5
q6
ik +
2
2
2EI
= M =
ψ
l
2EI
⎛
l ⎝
q
~
− q
~
⎞
l ⎠
l
6EI
2EI
l
l
6EI
2EI
l
5 2
( 2ϕ
)
~ ~
~ ~ ~ ~
k + ϕi
− 3 ik = ⎜2q6
+ q3
− 3 ⎟ = q2
+ q3
− q5
q6
ki +
2
2
6EI
= −T
=
ψ
l
6EI
⎛
q
~
− q
~
⎞
l ⎠
l
12EI
6EI
l
12EI
4EI
l
5 2
( ϕ
)
~ ~
~ ~ ~ ~
i + ϕk
− 2 ik = ⎜q3
+ q6
− 2 ⎟ = q2
+ q3
− q5
q6
ik +
2
2
3
2
3
6EI
6EI
⎛
= T ( )
~
ki = − ϕ
2 i + ϕk
− 2ψ
ik = − ⎜q
2
l
l ⎝
12EI
~ 6EI
~ 12EI
~ 6EI
= − q
~
3 2 − q
2 3 + q
3 5 − q
2
l l l l
l
⎝
3
6
+ q
~
6
q
~
q
~
− 2
− q
~
⎞
l ⎠
Summarising these calculations yield the following stiffness matrix for the plane beam element
~
K
e
⎡
⎢
⎢
⎢ 0
⎢
⎢
⎢ 0
= ⎢
⎢−
⎢
⎢
⎢
⎢
⎢
⎣
EA
l
EA
l
0
0
12EI
l
6EI
l
12EI
−
3
l
6EI
l
0
3
2
0
2
0
6EI
2
l
4EI
l
0
6EI
−
2
l
2EI
l
5
− q
~
l
−
2
EA
l
0
0
EA
l
0
0
⎞
⎟
⎠
=
l
0
12EI
−
3
l
6EI
−
2
l
0
12EI
3
l
6EI
−
2
l
l
⎤
0 ⎥
6EI
⎥
⎥
2
l ⎥
2EI
⎥
l ⎥
⎥
0 ⎥
⎥
6EI
⎥
−
2
l
⎥
4EI
⎥
⎥
l ⎦
It is worth to note, that the element stiffness matrices are symmetric. This is the consequence of
the reactions reciprocity theorem (Rayleigh’s theorem) stating that
k ij = k ji
The physical interpretation of the entries in this matrix is unchanged, i.e. for instance the second
column collects the values of reactions created by the action of the displacement q ~
1 .
After the derivation of these two examples of the element stiffness matrices let us now deal with
the loading. Generally, the loading is split into actions directly at the nodes and the actions along
the elements. The former one will be considered at the later stages. The latter one must be
transferred to the nodes in the form of appropriate reactions. They are assembled into a vector of
reactions due to the span loading
~
R
~
[ R0
i
] 1,2,..., 6
0 e =
6× 1
i =
This vector enters the equation of element equilibrium as an additional term
l
2 =
6EI
l
2

~ ~ ~ ~
R = K q + R
e e e 0e
For instance, in the case of the uniformly distributed load on the beam we have
~
R01
~
R03
i
~
R04
x ~
k ~
R06
e
l ~
R05
~
R02
y ~
~
R
0e
⎡ ~
R
⎢ ~
⎢R
⎢ ~
R
= ⎢ ~
⎢R
⎢ ~
⎢
R
~
⎢⎣
R
01
02
03
04
05
06
⎡ 0 ⎤
⎤ ⎢ ql ⎥
⎢ −
⎥ 2
⎥
⎥ ⎢ 2 ⎥
⎢ ql
⎥ − ⎥
⎥ = ⎢ ⎥
⎥ ⎢ 0 12 ⎥
⎥ ⎢ ql ⎥
⎢ −
⎥ ⎥
⎥ ⎢
2
2 ⎥
⎦ ⎢ ql ⎥
⎢⎣
12 ⎥⎦
and in the case of the non-uniform heating ∆t with warmer upper side and the uniform heating t 0
~
R01
~
R03
i
~
R04
x ~
∆t
+
t
k
0
~
–
R06
e l ~
R05
~
R02
y ~
~
R
0e
⎡ ~
R
⎢ ~
⎢R
⎢ ~
R
= ⎢ ~
⎢R
⎢ ~
⎢
R
~
⎢⎣
R
01
02
03
04
05
06
⎤ ⎡ EAαtt0
⎤
⎥ ⎢ ⎥
⎢
0
⎥
⎥
⎢
∆t
⎥ EIα
⎥
t
⎥ = ⎢ ⎥
⎥ ⎢ − EAα
h tt0
⎥
⎥ ⎢ ⎥
⎥ ⎢
0
⎥
⎢
∆t
⎥ − ⎥
⎦
EIαt
⎢⎣
h ⎥⎦
In the latter case note that the distribution of the bending moment is constant with the fibres under
tension on the colder side. Hence, the shear force is zero leading to zero reactions number 2 and
5. On the other hand, the uniform heating leads to the constant compressive axial force.
To obtain the stiffness matrices for another types of beams with degenerate supports, e.g. the
clamped-hinged beam, the clamped-slider beam, etc. the process of static condensation can be
used.
In general, the process uses the fact, that some reactions in the degenerate supports are zero. In
the case of the hinge the moment is zero. From this condition the corresponding displacements
can be eliminated and the dimension of the matrix is reduced from 6 by a number of zero reaction.
The equilibrium conditions can be rearranged as:
⎡~
R
⎢~
⎢⎣
R
e1
ec
⎤ ⎡~
K
⎥ = ⎢~
⎥⎦
⎢⎣
K
and the reactions in degenerate supports
~ ~ ~ ~
R = K q + R
e e e 0e
e11
ec1
~
K
~
K
e1c
ecc
~
R ec = 0
⎤⎡q
~
⎥⎢~
⎥⎦
⎣q
e1
ec
⎤ ⎡~
R
⎥ + ⎢~
⎦ ⎢⎣
R
0e1
0ec
⎤
⎥
⎥⎦

⎪⎧
~ ~ ~
Re1
= Ke11q
~
e1
+ Ke1c
q
~
⎨ ~ ~
⎪⎩ 0 = K
~
ec1qe1
+ K
~
eccqec
From the second equation vector of displacements
can be substituted into the first equation
to get
~
R
e1
ec
~
+ R
~
+ R
0e1
0ec
~
( Kec1q
~
e1
R ec )
~ −1 ~
ec = −Kecc
0
q
~
+
e11
e1
e1c
−1
ecc
~ ~ ~
( K
~
ec1qe1
+ R0ec
) R0e1
~ ~ ~ ~ ~
R = K q − K K
+
=
~ ~ ~ −1~
( )
~ ~ ~ ~ −1~
Ke11
− Ke1cK
ecc Kec1
qe1
+ ( R0e1
− Ke1cK
ecc R ec )
e1
0
where the expressions in the parentheses are the modified stiffness matrix and the modified vector
of reactions due to loading, respectively.
~ ~ ~ ~ −1~
Ke'
= Ke11
− Ke1cK
ecc Kec1
~ ~ ~ ~ −1~
R ' = R − K K R
So we have
0e
0e1
e1c
ecc
~ ~ ~ ~
R = K ' q + R
e1 e e1
0e
The static condensation is very simple if just one displacement at a time is eliminated using the
single condition of the zero reaction. For instance if the displacement q ~ r is eliminated, then
'
0ec
⎧~
~ ⎪k
K e':
⎨
⎪~
⎩k
ln
ln
' = k
~
' = 0
ln
− k
~
for
lr
~
~ 1 krn
for l ≠ r
krr
l = r or n = r
and
n ≠ r
~
R
0e
⎧ ~
⎪R
': ⎨
⎪ ~
⎩R
0l
0l
' = R
~
' = 0
0l
− k
~ ~
lr ~ 1 R
krr
for l = r
0r
for
l
≠ r
So schematically we have
n
r
n
r
l
k ~
ln
k ~
lr
~
R 0l
l
~
k ln
'
0
0
~
R 0l
'
0
r
k ~
rn
k ~
rr
~
R 0r
r
0 0 0 0 0
0
0
In the case of static reduction of several displacements this can be carried out step by step, one
displacement after another.
For the clamped-hinged elements we have:

~ q
~
~
K ' =
e
⎡
⎢
⎢
⎢
⎢
⎢
⎢
⎢
⎢−
⎢
⎢
⎢
⎢
⎣
EA
l
0
0
EA
l
0
0
i
R 1,
1
2
~ R , q
~
3
3
~ R 4,
q
~
x ~
~
4
R 4,
q
~
4
x
k
~
k
~
~
R
e
R 6 = 0
6,
q
~
6
e
~ ~ i
~ R
~
R
5,
q
1,
q 1
~
5
R 5,
q
~
5
~ R
~
2,
q
~ R
~
2,
q
R ~
2
3 = 0
y ~ y ~
0
3EI
3
l
3EI
2
l
0
3EI
−
3
l
0
0
3EI
2
l
3EI
l
0
6EI
−
2
l
0
−
EA
l
0
0
EA
l
0
0
0
3EI
−
3
l
3EI
−
2
l
0
3EI
3
l
0
⎤
0⎥
⎥
0⎥
⎥
⎥
0
⎥
⎥
0⎥
⎥
⎥
0
⎥
0⎥
⎦
~
K
⎡ EA
⎢ l
⎢
⎢ 0
⎢
⎢ 0
' = ⎢ EA
⎢
−
l
⎢
⎢ 0
⎢
⎢
⎢
0
⎣
Example
Elimination of q
~
3 in the case of the hinged-clamped beam.
Let us check the value k 52 ' (l = 5, n = 2, r = 3)
~
k
52
' = k
~
52
− k
~
53
~
~ 1 k
k
33
32
e
12EI
− 6EI
1
= − − ⋅
3 2
l l 4EI
l
0
3EI
3
l
0
0
3EI
−
3
l
3EI
2
l
6EI
⋅
2
l
0
0
0
0
0
0
−
3EI
= −
3
l
~
Let us also calculate R ' for the case of point load at the beam centre (l = 6, r = 3)
06
EA
l
0
0
EA
l
0
0
0
3EI
−
3
l
0
0
3EI
3
l
3EI
−
2
l
⎤
0 ⎥
3EI
⎥
⎥
2
l ⎥
0 ⎥
⎥
0
⎥
3EI
⎥
− ⎥
2
l ⎥
3EI
⎥
l ⎥⎦
~
R
03
Pl
= −
8
~ Pl
R 06 =
8
R ~
03 ' = 0
~
R
06
'
~ ~ ~ ~ 2 1 3
~ 1 Pl EI ⎛ Pl ⎞ Pl
R 06'
= R06
− k36
R03
= − ⋅ ⋅ ⎜ − ⎟ =
k 8 l 4EI
8 16
33
⎝ ⎠
l
The 2D beam can be generalised to the 3D case. To this end we must include bending and shear
in two planes as well as torsion.
~ R 9,
q
~
9
z ~
~
x ~
R 8,
q
~
~
k
~
8 R
R
~
12,
q
~
12
7,
q 7
~
~ ~
R R 3,
q
11,
q
~
11
3
~ e
y ~ ~
~ i
R 10,
q
~
10
2,
q ~
2 R
~
6,
q 6
~ ~
~ R
~ R
1,
q
5,
q 5
1 ~ R , q
~
R
4 4

The complete stiffness matrix for the 3D beam has the following form
⎡ EA
EA
⎢ 0 0 0 0 0 − 0 0
l
l
⎢
12EI
⎢
z
6EIz
−12EIz
0 0 0
0
0
3
2
3
⎢ l
l
l
⎢
12EI
y 6EIy
−12EIy
⎢
0
0 0 0
3
2
3
⎢
l
l
l
⎢
GIs
0 0 0 0 0
⎢
l
⎢
4EIy
− 6EI
y
⎢
0 0 0
⎢
l
2
l
⎢
4EIz
− 6EIz
⎢
0
0
~
=
l
2
K ⎢
l
e'
0
⎢
EA
0 0
⎢
l
⎢
12EIz
⎢
0
3
⎢
l
⎢
12EIy
⎢
3
l
⎢
⎢ s y m m e t r y
⎢
⎢
⎢
⎢
⎢
⎣
0
0
0
− GI
l
0
0
0
0
0
GI
l
s
s
6EI
l
2EI
− 6EI
l
0
0
y
2
0
l
0
0
0
2
0
4EI
l
y
y
y
6EI
l
2EI
l
− 6EI
The unmodified stiffness matrix of any element is singular. This matrix is obtained for a structure
without any supports for which the rigid body movements are not eliminated. For instance the
plane beam element has three rigid body movements (degrees of freedom)
l
0
z
2
0
0
0
0
2
0
0
0
4EI
l
z
z
z
⎤
⎥
⎥
⎥
⎥
⎥
⎥
⎥
⎥
⎥
⎥
⎥
⎥
⎥
⎥
⎥
⎥
⎥
⎥
⎥
⎥
⎥
⎥
⎥
⎥
⎥
⎥
⎥
⎥
⎥
⎦
u
v
ϕ
The structures are usually assembled of many elements for which the local co-ordinate systems
are oriented in various ways. To analyse efficiently the entire structure all the variables must be
expressed in one selected global system of co-ordinates. Hence, the local variables for each
element must be transformed to the global co-ordinates.
Let us consider a 3D element with its own local co-ordinates
z
k
x ~
x
z ~
u i
i
y ~
w i
v i
u ~
i
y
e
The nodal displacements for the node i can be related to the local co-ordinates
or to the global co-ordinates xyz:
q
n,
e
⎡ui
⎢
=
⎢
v i
⎢⎣
wi
⎤
⎥
⎥
⎥⎦
x ~ y
~ z
~ : q
~
n,
e
⎡u
~
i
⎤
⎢ ⎥
= ⎢v
~
i ⎥
⎢ ⎥
⎣w
~
i ⎦

For instance the local displacement u ~ i can be expressed in terms of global displacements
where the notation
( x
~
, x) + v cos( x
~
, y ) + w cos( x
~
z)
u
~
i = ui
cos
i
i ,
cos
( a , b) = cos[ ∠( a,
b)
]
was used to denote the cosine of the angle between two axes. These cosines are called the
direction cosines and can be assembled into one matrix C
⎡cos
⎢
C = ⎢cos
⎢
⎣cos
( x
~ , x) cos( x
~ , y ) cos( x
~ , z)
⎤
( y
~
, x) cos( y
~
, y ) cos( y
~
, z)
( ) ( ) ( )⎥ ⎥⎥ z
~
, x cos z
~
, x cos z
~
, z ⎦
which relates the vectors of displacements in the local and global co-ordinates
q
~
= Cq
n , e n,
e
The analogue relation can be found for the vectors of nodal rotations
⎡~
ϕxi
⎤ ⎡ϕ
xi ⎤
⎢~
⎥ ⎢ ⎥
⎢
ϕyi
⎥
= C
⎢
ϕyi
⎥
⎢~
⎣ϕ
⎥⎦
⎢⎣
⎥
zi ϕzi
⎦
For the entire vector of element displacements for the 3D beam we get
q
~
= T q
where the transformation matrix is
T e
e
⎡C
⎢
⎢
0
=
⎢0
⎢
⎣0
The transformation matrix T e is quasi-diagonal and orthogonal (i.e. T e T = T e –1 ), hence the inverse
relation involves just the transpose of T e
q
e
0
C
0
0
= T
The same matrix is used to transform the vectors of forces
~
Re
= TeR
e
T ~
R = T R
e
The transformation of the element stiffness matrix requires a more complicated procedure. Let us
start with the element equilibrium in local co-ordinates
e
T
e
e
e
0
0
C
0
q
~
e
e
~ ~ ~ ~
R = K q + R
0⎤
⎥
0
⎥
0⎥
⎥
C⎦
e e e 0e
and let us substitute the expressions for the local vectors of forces and displacements to get
~
T R = K T q + T R
e e e e e e 0e
This equation can be multiplied from the left-hand side by T e
T
~
T +
T
T
T
e TeR
e = Te
KeTeqe
Te
TeR
0e

Since
we get
or
T
e
T T = I
~
R +
e
T
T
e = Te
KeTeqe
Te
R0e
R = K q + R
e e e 0e
with the element stiffness matrix in the global co-ordinates
and the vector of nodal reactions due to the span loading in the global co-ordinates
T ~
R = T R
K
e
= T
T
e
~
K
e
T
e
0e e 0e
R e is the corresponding vector of reactions expressed in the global co-ordinates.
In the case of the plane beam element the transformation matrix has the form
T e
⎡C
0⎤
= ⎢ ⎥
⎣0
C⎦
where the component matrix C is related to the transformation of the nodal displacement vector
q
n,
e
⎡ui
⎤
⎢ ⎥
=
⎢
v i ⎥
⎢⎣
ϕ ⎥
i ⎦
In this situation the axis z and z ~ coincide and the matrix C has the form
⎡cos
⎢
C = ⎢cos
⎢
⎣cos
( x
~ , x) cos( x
~ , y ) cos( x
~ , z)
( y
~ , x) cos( y
~ , y ) cos( y
~ , z)
( z
~ , x) cos( z
~ , x) cos( z
~ , z)
⎤ ⎡ cosα
⎥ ⎢
⎥ =
⎢
cos
⎥
⎦
⎢⎣
0
( π 2 + α )
cos
( π 2 − α )
cosα
0
0⎤
⎡ cosα
⎥ ⎢
0
⎥
=
⎢
− sinα
1⎥⎦
⎢⎣
0
sinα
cosα
0
0⎤
⎥
0
⎥
1⎥⎦
α
y ~
z ~ =
z
y
α
x ~
x
The transformation of the element stiffness matrix can be given in terms of submatrices. If we
represent the stiffness matrix in the local co-ordinates for an element e with nodes i and j as
then the transformation follows as
K
e
⎡C
= ⎢
⎣0
0⎤
⎥
C⎦
T
⎡~
K
⎢~
⎢⎣
K
ii,
e
ji,
e
~
K
e
~
K
~
K
⎡~
K
= ⎢~
⎢⎣
K
ij,
e
jj,
e
ii,
e
ji,
e
⎤⎡C
⎥⎢
⎥⎦
⎣0
Similarly for the vector of reactions we can write down
~
K
~
K
ij,
e
jj,
e
⎤
⎥
⎥⎦
⎡ T ~
0⎤
C K
⎥ = ⎢
T ~
C⎦
⎢⎣
C K
ii,
e
ji,
e
C
C
T ~
C Kij
T ~
C K
, e
jj,
e
C⎤
⎥
C⎥⎦

and the transformation takes the form
R
~
R
⎡~
R
= ⎢
⎢⎣
R
0i,
e
0 e ~
0 j,
e
⎡~
R
⎢~
⎢⎣
R
⎤
⎥
⎥⎦
⎤ ⎡ ~
C
⎥ = ⎢
⎥⎦
⎢⎣
C
T
T
⎡C
0⎤
0i,
e R0i,
e
0 e = ⎢ ⎥
T ~
⎣0
C⎦
0 j,
e R0
j,
e
⎤
⎥
⎥⎦
In the case of the plane truss element the difference with respect to the plane beam element is,
that the former one does not involve nodal rotations. Hence, the transformation matrix is
T e
⎡ cosα
⎢
⎢
− sinα
=
⎢ 0
⎢
⎣ 0
sinα
cosα
0
0
0
0
cosα
− sinα
0 ⎤
⎥
0
⎥
sinα
⎥
⎥
cosα
⎦
The element stiffness matrices after transformation to the uniform global set of co-ordinates can be
assembled to yield the stiffness matrix for the entire structure. We describe this assemble process
for an exemplary case of plane beam elements.
Let us represent the equilibrium conditions for an element e in global co-ordinates using the split of
matrices and vectors into part corresponding to the nodes of the element (i and j)
⎡R
⎢
⎣R
i,
e
j,
e
⎤ ⎡K
⎥ = ⎢
⎦ ⎣K
ii,
e
ji,
e
K
K
ij,
e
jj,
e
⎤⎡qi
⎥⎢
⎦⎣q
j
, e
, e
⎤ ⎡R
⎥ + ⎢
⎦ ⎣R
Now let us consider a node i in a structure, where n-elements meet. The node is loaded by the
external generalised forces P xi , P yi and P ϕi . Let the directions of displacements at this node be
denoted by m, (m + 1) and (m + 2). So the nodal forces can also be denoted as
⎡P
⎢
P i = ⎢P
⎢
⎣P
xi
yi
ϕi
⎤ ⎡ P
⎥ ⎢
⎥ ≡
⎢
Pm
⎥
⎦
⎢⎣
Pm
The reactions in the elements meeting at the node i are already transformed to the global set of coordinates
xy and can be expressed as
m
+ 1
+ 2
⎤
⎥
⎥
⎥⎦
R +
0i,
e
0 j,
e
i , e = Kii,
eqi,
e + Kij,
eq
j,
e R0i,
e
⎤
⎥
⎦
e
R i3,e
R i2,e
R i1,e
2
n
i
P m
y
P m+2
P m+1
1
x
The reactions from all the elements meeting at the node i acting on the node (taken with opposite
magnitude) and the external forces must be in equilibrium

or
n
− ∑R
e = 1
P
i, e + i =
0
n
∑ ( K ii, eqi,
e + Kij,
eq
j,
e + R0i,
e
) − Pi
= 0
e = 1
The displacements in the vector q i,e are common for all the elements at the node i, while those in
the vectors q j,e correspond to the opposite ends of the elements and thus are not common. Hence,
we can rewrite the equilibrium as
⎛
⎜
⎝
n
∑
e = 1
n
n
⎛
( ) ⎟ ⎞
∑ Kij,
eq
j,
e = Pi
−
⎜∑
0i,
e
e = 1
⎝ e = 1 ⎠
⎞
K ii, e
⎟qi,
e +
R
⎠
This set of equations written for the node i comprises three equations which can be represented as
m m+1 m+2
m
q m
m+1
· q m+1 =
m+2
n
∑
e=
1
K
ii,
e
Fragment of global stiffness matrix K
K ij,e
q m+2
Fragment of
global vector of
displacements q
P
− ∑
n
i R i , e
e=
1
Fragment of
global vector of
forces P
On the other hand we can also consider a contribution of one element e with the nodes i and j in
the form of the element matrix
K
e
⎡K
= ⎢
⎣K
and the element vector of reaction due to the span loading
R
0e
ii,
e
ji,
e
⎡R
= ⎢
⎣R
to the global stiffness matrix K and the global vector of forces P, respectively. The global set of
equilibrium equations can therefore be written down as
K
K
0i,
e
0 j,
e
Kq = P
The square matrix K has the dimension k×k and the vector P – k, where k is the number of all
nodal displacements in the entire structure.
Let us assume that the node i of the element coincides with the structure node with the
displacements numbered as m, (m + 1) and (m + 2) and the element node j – with the structure
node with the displacements numbered as n, (n + 1) and (n + 2).
We have
ij,
e
jj,
e
⎤
⎥
⎦
⎤
⎥
⎦

m+1
m m+2
n
n+1
n+2
m
m+1
m+2
n
n+1
n+2
K ii,e
K ij,e
K ji,e K jj,e
–R 0i,e
–R 0j,e
In the case of elastic support in the direction of the displacement (m + 1) at a node i
F m+1
e
i
n
P m
2
P m+2
P m+1
1
an additional force F m+1 due to the displacement in the support must be considered. This force has
always the orientation opposite to the displacement because the spring counteracts it. Hence, the
this force is with the positive sign on the left hand side of the global set of equations. This force is
obtained from the formula
F
kq
m+ 1 = m+1
where k is the spring stiffness. So the small modification of the global stiffness matrix is enough.
Namely, in the (m + 1)-equation a term kq m+1 must be added, what leads to a simple addition of the
spring stiffness k to the element (m + 1)-(m + 1) of the global stiffness matrix K.
Let us now consider an example of the assembly process of the matrix K and the vector P for a
given plane frame.
M
1 2
1 2
3
q
P
3 4
4 5 y
x

The frame consists of four beam elements which are interconnected in five nodes. The element
stiffness matrices and vectors of nodal reactions due to the span loading are found in the local coordinates
for each element
1 2 1 1
1
1
1
x ~
2
y ~ x ~
3
y ~
4
y ~ x ~
y ~ x ~
2
2
are transformed to the global co-ordinates
1 2 2 3
1 x
2
y
y
and they can be represented as
x
⎡K11,1
K12,1
⎤ ⎡K11,2
K12,2
⎤ ⎡K11,3
K12,3
⎤ ⎡K11,3
K12,3
⎤
K 1 = ⎢ ⎥ K 2 = ⎢
⎥ K 3 = ⎢
⎥ K 1 = ⎢
⎥
⎣K
21,1 K22,1⎦
⎣K
21,2 K22,2
⎦ ⎣K
21,3 K22,3
⎦ ⎣K
21,3 K22,3
⎦
Note, that the local element numbers of element nodes can be replaced with the global numbers:
Element 1: 1 – 1, 2 – 2, element 2: 1 – 2, 2 – 3, element 3: 1 – 2, 2 – 4, element 4: 1 – 3, 2 – 5.
These relations enable a proper “addressing” of the subsequent submatrices of the element
stiffness matrices K e in the global stiffness matrix of the frame K. The assembly scheme is
2
4
3
y
x
3
y
4
5
x
K =
K 11,1 K 12,1
K 21,1
K 22,1+K 11,2+
+K 11,3
K 12,2
K 12,3
K 21,2 K 22,2 +K 11,4 K 12,4
K 22,3
K 21,3
K 21,4 K 22,4
Note, that in this scheme each box corresponds to a node and it represents 3×3 elements of the
global stiffness matrix corresponding to three displacements at the given node.
Let us also consider the assembly of the global force vector P.
Out of four beams constituting the frame only one – No. 4 has a span loading and consequently
the non-zero vector of reactions due to the loading. These vectors for the other beams are zero:
~ ~ ~
R R = R = R = R = R = 0
01 = 02 03 01 02 03
To calculate the vector for the fourth element the loading can be split into uniformly distributed load
acting along the beam and transverse to the beam
q
q 1 l
q 2
2 l
2
12
q q 2 l
1 = qsinϕcosϕ
q 2 qcos 2 ϕ
l
=
+ 2
l
ϕ
l 2 l
q 1 l
2 2
2 l
2
12

Now the vector of reactions can be set up
~
R
04
⎡ ~
R
⎢ ~
⎢R
⎢ ~
R
= ⎢ ~
⎢R
⎢ ~
⎢R
⎢ ~
⎣R
01,4
02,4
03,4
04,4
05,4
06,4
and transformed to the global set of co-ordinates
with the transformation matrix
⎡C
T = ⎢
⎣0
0⎤
⎥
C⎦
R
04
= T
⎡ ql sinϕ
cosϕ
⎤
⎢−
2
⎥
⎢
2 ⎥
⎤ ⎢ ql cos ϕ
−
⎥
⎥ ⎢ 2 ⎥
⎥ ⎢ 2 2
ql cos ϕ ⎥
⎥ ⎢ −
⎥
⎥ = ⎢
⎥
⎥ ⎢ ql sin 12 ϕ cosϕ
−
⎥
⎥ ⎢ 2 ⎥
⎥ ⎢
2
ql cos ϕ ⎥
⎥ ⎢ −
⎥
⎦
⎢ 2 ⎥
2 2
⎢ ql cos ϕ ⎥
⎢
⎣ 12
⎥
⎦
T
4
~
R
04
⎡R
= ⎢
⎣R
01,4
02,4
⎤
⎥
⎦
⎡ cosϕ
⎢
C =
⎢
− sinϕ
⎢⎣
0
sinϕ
cosϕ
The nodal external forces P and M are directly substituted into the vector of loading P, the force P
opposite to the x axis with the negative sign in the first of three places in the box corresponding to
the node 3 and the clock-wise moment M with the positive sign to the third place in the box
corresponding to the node 2.
0
0⎤
⎥
0
⎥
1⎥⎦
P =
–P
0
0
0
0
M
–R 01,4
–R 02,4
The global stiffness matrix K for the entire frame has a characteristic band structure. If this band is
narrow a computer storage saving is possible. Hence, it is advisable to keep the band width as
small as possible. The width depends on the order of node numbering. The difference between the
node numbers for a single element should be kept as small as possible. Let us consider two cases
of the numbering
1 2 3 4 5
6 7 8 9 10
11 12 13 14 15
1 4 7 10 13
2 5 8 11 14
3 6 9 12 15
In the first case the maximum difference of node numbers for a single element equals to 5 and in
the second case – to 3. The latter one is therefore more efficient because the band width in the
global stiffness matrix will be smaller.
The band width b can be computed as

[ max i − + 1]
b = s ⋅ j
where s is the number of degrees of freedom per node and i and j are the node numbers for a
single element. The band-structured matrix can be stored in the computer memory as a single
column consisting of the elements in the band read row-wise or as a rectangular matrix with the
dimensions b×n, where n is the global number of unknown displacements for the structure.
The assembled global stiffness matrix K is singular, because it is representing a structure without
any supports, still possessing freedom of rigid body rotations. To remove the singularity the
support conditions must be introduced to the system of equilibrium equations
Kq = P
The k-th equation in this set corresponds to the condition, that the reaction in an additional fictitious
k-th support is zero, as was the case in the classical stiffness method. On the other hand, if the k-
th support does exist, then the corresponding reaction is not zero. Thus, the k-th equation is
spurious. Consequently, the corresponding displacement q k is zero, hence all the elements from
the k-th column in the matrix K multiply the zero value and are spurious, too. So, the direct method
of inclusion of support conditions in the equilibrium equations would be to remove the rows and
columns from the matrix K corresponding to the real support as well as removing the
corresponding element from the vector P. This method, though correct, is not effective numerically,
because it would require a complex process of renumbering of unknowns.
Instead one of several indirect methods are used in computer practice. The first one introduces a
elastic support with an “almost” infinite spring stiffness. This leads to a simple addition to the
element (k,k) in the matrix K of a large number, several orders of magnitude larger then the
maximal element of the entire matrix K.
The second method modifies the k-th equation to a form
1 ⋅ q = 0
k
which automatically yields the zero displacement q k in the support. This is done by zeroing the k-th
element of the vector P and all the elements of the k-th row of the matrix K except for the element
(k,k), which is set to 1. Additionally, also all the elements of the k-th column of the matrix K are set
to zero to eliminate those that are unnecessary due to their multiplication by the zero displacement
q k .
Existence of hinge connections in the plane frame requires special care in the analysis. For
instance in the following example
1 2
1 2
elements 3 and 4 meeting at the node 3 have two different angles of cross-section rotation there.
So the real number of unknowns in the node 3 is four. If the computer program allows for such a
situation no problem exists. But if on the other hand the number of unknowns per node is fixed
than special precautions must be made. If both the elements are taken as the clamped-hinged
ones with the stiffness matrices after the static condensation, than the global stiffness matrix K will
be singular because there are no non-zero entries to the row and column k corresponding the
rotation(s) in the node 3, including 0 on the main diagonal. This yields the singular equation
0 ⋅ q = 0
One way to overcome this problem is to treat one of the elements adjacent to the hinge, for
instance the element 3, as the clamped-clamped one with the element matrix without static
k
3
3 4
4 5

condensation. Then, the matrix K will not be singular and the angle of rotation at the hinge in the
element 3 will be automatically calculated as one of the unknowns. The element 4 is therefore
considered as the hinged-clamped one and its stiffness matrix is obtained from the static
condensation.
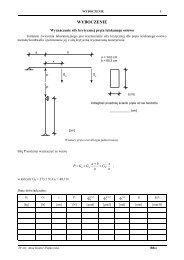
Influence of support displacements can also be included in the analysis.
These displacements for an element can be assembled into a vector q ~
∆e
. Like all the nodal
displacements, they lead to the nodal reactions in elements according to the equilibrium equation
for the element
~
( q
~
e + q
~
e ) R e
~ ~
R +
e = Ke
∆ 0
The influence of these displacements can be included in the vector of reactions due to the span
loading
~ ~
( Keq
~
e R e )
~ ~
R
~
+
e = Keqe
+ ∆ 0
Thus, if there is no other loading the support displacements are the only factor influencing the
reactions vector
~ ~
R = K q
~
Let us consider an example
1
0 e
e
∆e
2
2
y ~ x ~
ϕ
γ
∆ x
∆
∆ y
Here only the element 2 has “adjacent” support displacements and only its vector of reactions will
be non-zero. The applied support displacements must be expressed in the local co-ordinates of the
element
∆
∆
x
y
= ∆ sinϕ
= ∆ cosϕ
and the local vector of support displacements for the element 2 is
q
~
∆2
⎡ 0 ⎤
⎢ ⎥
⎢
0
⎥
⎢ 0 ⎥
= ⎢ ⎥
⎢∆
x ⎥
⎢∆
⎥
y
⎢ ⎥
⎢⎣
− γ ⎥⎦
Note, that the displacements must be substituted with appropriate sign according to their
orientation with respect to the local axes. Therefore, the anti-clockwise rotation is taken as
negative.
Having this vector of displacements the corresponding vector of reactions can be calculated,
transformed to the global co-ordinates and used in the assembly process of the vector of nodal
forces P.

Let us now set the entire algorithm of the matrix version of the stiffness method for the plane
frames.
1. Assume the global co-ordinate system. Number the nodes and element. Select the local
systems of co-ordinates. Attach the internal hinged connections to the elements leaving one
element at a hinge as clamped-clamped.
2. Calculate local stiffness matrices K ~ e for the elements with the static condensation for the
hinged-clamped ones. Transform the local matrices to the global co-ordinates to get K e
T ~
K = T K T
e
3. Assemble the global stiffness matrix K for the entire system from all the element matrices K e
expressed in global so-ordinates.
~
4. Calculate the vectors of reactions R 0e
due to the span loading: forces on the beams, uniform
and non-uniform heating, support displacements. Transform these vectors to the global coordinates
to get R 0e .
e
e
~
e
T
0e Te
R0e
R =
5. Assemble the vector of nodal forces P for the entire system from all the element vectors R 0e
taken with the negative sign and all the external nodal loading.
6. Include the supports in K and P. For the rigid supports set to zero all the corresponding
elements in P and all the elements in the corresponding rows and columns of K except for the
main diagonal term to be set to 1. For the flexible supports add the spring stiffness to the
corresponding main diagonal term in K.
7. Solve the global set of equilibrium equations
Kq = P
to get the nodal displacements in global co-ordinates.
8. Select the displacements for the separate elements and form the appropriate vectors q e .
Transform these vectors to the local co-ordinates to get q ~
e
q
~
= T q
e
9. Compute the reactions at the element ends from the equilibrium conditions for the separate
elements
e
e
~ ~ ~ ~
R = K q + R
e e e 0e
These reactions correspond to the values of internal forces at the element ends
~
R
e
⎡ ~
R
⎢ ~
⎢R
⎢ ~
R
= ⎢ ~
⎢R
⎢ ~
⎢
R
~
⎢⎣
R
1
2
3
4
5
6
⎤ ⎡−
N
⎥ ⎢
⎥ ⎢
−T
⎥ ⎢ Mik
⎥ = ⎢
⎥ ⎢ Nki
⎥ ⎢ Tki
⎥ ⎢
⎥⎦
⎢⎣
Mki
ik
ik
⎤
⎥
⎥
⎥
⎥
⎥
⎥
⎥
⎥⎦
At the end let us summarise some “tricks” related to the matrix version of the stiffness method.
1. Flexible support as an additional element
k EA
= k , EI = 0
l

2. A truss can be solved using the beam elements if one element of those meeting at a node is
treated as clamped.
For the hinged-hinged elements the static condensation of the matrix for clamped-hinged element
can be carried out to eliminate the second rotation.
3. Curved beams can be analysed in an approximate way by modelling the curve as an assembly
of a sufficiently large number of straight-line beams
4. Similarly, tapered elements can be modelled as assemblies of piece-wise constant cross-section
elements.
5. Calculation of displacement at an arbitrary point of an element
A
v A
q
q
~
3
q
~
q
~
1
2
v A0
A
q
~
5
q
~
6
q
~
4
The arbitrary displacement can be calculated using the superposition rule applied to the influences
of the support (nodal) displacements and the span loading. Hence, we have
v
A
= v
A0
The displacements along the element due to the nodal displacements are calculated using so
called shape functions. In the case of the beam element axial nodal displacements do not cause
transverse displacements in the beam. So the non-zero shape functions are due to the
displacements 2, 3, 5 and 6. They have the form
q
~
v A6
q
~
6
3
A
A
A
q
~
2
v A2
v A3
+
6
∑
i = 1
v
~
Ai q i
v A5 q
~
5
A
and the exact mathematical expressions will be derived in the following section on matrix analysis
of stability of frames.

6. Calculation of envelopes of static and kinematic quantities under a set of moving loads.
For instance let us consider the envelope of bending moments in the beam presented in the figure
q P 1 P 2
The classical approach involves calculation of influence lines. They are found for the moments at
several number of points along the beam. Each influence line is loaded by the load set in the way
leading to the extreme output moments (positive and negative) calculated from the superposition
rule.
0 1 2 etc.
M 0 (x)
q P 1 P 2
M 1 (x)
M 2 (x)
etc.
S
η 1
η 2
M
M
2max
2min
= max
= min
( qS + P1
η1
+ P2η
2 )
( qS + Pη
+ P η )
These maximum values are then put together to yield the envelope.
1
1
2
2
0 1 2 etc.
M 2min
M 2max
etc.
7. Solving a set of algebraic equations
AX = B
For a simple calculation of unknowns X the main matrix of coefficients A can be decomposed into
a product of two triangular matrices
A = A 1 A 2
=
0
·
0
to get
The product
A A X = B
1
2
A 2 X =
Z

gives an auxiliary vector and the original set of equations is represented as a combination of two
sets of equations
A Z = B
1
A X = Z
2
Each of these sets is characterised be a triangular coefficient matrix and can be easily solved
equation after equation by a method of back substitution.
The decomposition into two triangular matrices can be done be several methods, e.g. the classical
Gauss elimination method or the Choleski method. In the latter one
so we have
T
2
A = A = S
1
T
S SX = B
and the process of back substitution is even simpler because just one triangular matrix S must be
stored in the computer memory.
Example
Let us find the distribution of internal forces in the following frame using the matrix version of the
stiffness method.
10
20kN/m
Data:
8
E = 205 GPa
7
9 2
x
20kN 2 β k
k = 57195 kN/m
4
y
β = arctan2/5 = 21.801°
6 5
Element 1:
A = 27.9cm 2
1
4
I = 1450cm 4
3
l = 4m
Element 2:
1
5
[m]
A = 46.1 cm 2
2
I = 4250 cm 4
l = 5.3852 m
In the solution we will use the method without constant number of unknowns in the node. The
hinge connecting both elements is therefore the node with four unknown displacements including
two separate angles of rotation, one for each element.
Both elements will be considered as clamped-hinged ones and the corresponding stiffness
matrices and vectors of reactions will be found for such elements. In the following figures
displacement directions for both elements are shown in local and global co-ordinates and the angle
α for the transformation is found.
4 x ~ 1
6
5
5
6
4
x ~
α = 270°
3
3
y
2
α x
1
1
2
1
Local co-ordinates Global co-ordinates Transformation

1
6
α = 360°–β = 338.199°
4 x ~ 6
4
3
2 5
3
x ~ 2 5
β
2
1
α x
y ~ 2
Local co-ordinates Global co-ordinates Transformation
Now we can associate the numbers of nodal displacements in the elements expressed in global
co-ordinates (from 1 to 6 for each element) with the numbers of nodal displacements in the global
numbering (from 1 to 10 in the considered example). Thus the allocation table is created
Element
Element directions
number 1 2 3 4 5 6
1 1 2 3 4 5 6
2 4 5 7 8 9 10
These allocations indicate, where the subsequent values from the element matrices and vectors in
global co-ordinates enter the global matrices and vectors for the entire structure. For instance: the
value k 52,2 from the stiffness matrix K 2 is added to the element k 59 in the global matrix K, the value
R 06,2 from the vector of reactions R 02 is subtracted from the element P 10 in the global vector P.
Now let us find the reactions vectors due to span loading. In this case only element 2 is loaded and
the loading is split into two components:
q
q
x
y
= 6sin β cos β = 2.0689 kN/m
2
= 6cos β = 5.1725 kN/m
6
6
3
q x
5
4
3
q y
5
4
1
2
1
2
For the clamped-hinged element the vector of reactions is
~
R
02
⎡ ~
R
⎢ ~
⎢R
⎢ ~
= ⎢
R
~
⎢R
⎢ ~
⎢R
⎢ ~
⎣R
01,2
02,2
03,2
04,2
05,2
06,2
⎡ qxl
⎤
⎢ ⎥
⎤ ⎢
3 2
q
⎥
⎢
yl
⎡ 5.5708 ⎤
⎥ − ⎥
⎢ ⎥
⎥ ⎢ ⎥
⎢
−10.446
⎥
⎥
⎥ ⎢ 0 8
⎥
⎢ ⎥
⎥ = ⎢ q
0
xl
=
⎢ ⎥
⎢ ⎥
⎥
⎢ ⎥
⎢ 5.5708 ⎥
⎥
⎢
5 2 q
⎥
⎢−
⎥
⎥
yl
17.409
−
⎢ ⎥
⎢ ⎥
⎥ 8
⎦
⎢⎣
18.750 ⎥
⎢ 2 ⎥
⎦
q l
⎢
y
⎥
⎢⎣
8 ⎥⎦
The element stiffness matrices in the local co-ordinates are

⎥
⎥
⎥
⎥
⎥
⎥
⎥
⎥
⎦
⎤
⎢
⎢
⎢
⎢
⎢
⎢
⎢
⎢
⎣
⎡
−
−
−
−
−
−
=
⎥
⎥
⎥
⎥
⎥
⎥
⎥
⎥
⎥
⎥
⎥
⎥
⎦
⎤
⎢
⎢
⎢
⎢
⎢
⎢
⎢
⎢
⎢
⎢
⎢
⎢
⎣
⎡
−
−
−
−
−
−
=
0
0
0
0
0
0
0
139.3
0
557.3
139.3
0
0
0
143000
0
0
14300
0
557.3
0
2229
557.3
0
0
139.3
0
557.3
139.3
0
0
0
143000
0
0
143000
0
0
0
0
0
0
0
3
0
6
3
0
0
0
0
0
0
3
0
3
3
0
0
3
0
3
3
0
0
0
0
0
~
3
2
3
2
2
3
2
3
1
l
EI
l
EI
l
EI
l
EA
l
EA
l
EI
l
EI
l
EI
l
EI
l
EI
l
EI
l
EA
l
EA
K
⎥
⎥
⎥
⎥
⎥
⎥
⎥
⎥
⎦
⎤
⎢
⎢
⎢
⎢
⎢
⎢
⎢
⎢
⎣
⎡
−
−
−
−
−
−
=
⎥
⎥
⎥
⎥
⎥
⎥
⎥
⎥
⎥
⎥
⎥
⎥
⎦
⎤
⎢
⎢
⎢
⎢
⎢
⎢
⎢
⎢
⎢
⎢
⎢
⎢
⎣
⎡
−
−
−
−
−
−
=
4854
901.3
0
0
901.3
0
901.3
167.4
0
0
167.4
0
0
0
175500
0
0
175500
0
0
0
0
0
0
901.3
167.4
0
0
167.4
0
0
0
175500
0
0
175500
3
3
0
0
3
0
3
3
0
0
3
0
0
0
0
0
0
0
0
0
0
0
3
3
0
0
3
0
0
0
0
0
~
2
2
2
3
3
2
3
3
2
l
EI
l
EI
l
EI
l
EI
l
EI
l
EI
l
EA
l
EA
l
EI
l
EI
l
EI
l
EA
l
EA
K
The transformation matrices are
⎥
⎦
⎤
⎢
⎣
⎡
=
C
0
0
C
T e
⎥
⎥
⎥
⎦
⎤
⎢
⎢
⎢
⎣
⎡
−
=
1
0
0
0
cos
sin
0
sin
cos
α
α
α
α
C
⎥
⎥
⎥
⎥
⎥
⎥
⎥
⎥
⎦
⎤
⎢
⎢
⎢
⎢
⎢
⎢
⎢
⎢
⎣
⎡
−
−
=
1
0
0
0
0
0
0
0
1
0
0
0
0
1
0
0
0
0
0
0
0
1
0
0
0
0
0
0
0
1
0
0
0
0
1
0
1
T
⎥
⎥
⎥
⎥
⎥
⎥
⎥
⎥
⎦
⎤
⎢
⎢
⎢
⎢
⎢
⎢
⎢
⎢
⎣
⎡
−
−
=
1
0
0
0
0
0
0
0.9285
0.3714
0
0
0
0
0.3714
0.9285
0
0
0
0
0
0
1
0
0
0
0
0
0
0.9285
0.3714
0
0
0
0
0.3714
0.9285
2
T
Now the transformation of local matrices and vectors to the global co-ordinates can be done.
⎥
⎥
⎥
⎥
⎥
⎥
⎥
⎥
⎦
⎤
⎢
⎢
⎢
⎢
⎢
⎢
⎢
⎢
⎣
⎡
−
−
−
=
=
18.750
18.233
1.2929
0
11.768
1.2929
~
02
2
02 R
T
R
T
⎥
⎥
⎥
⎥
⎥
⎥
⎥
⎥
⎦
⎤
⎢
⎢
⎢
⎢
⎢
⎢
⎢
⎢
⎣
⎡
−
−
−
−
−
−
−
−
=
=
0
0
0
0
0
0
0
24350
60460
0
24350
60460
0
60460
151300
0
60460
151300
0
0
0
2229
0
557.3
0
24350
60460
0
143000
0
0
60460
151300
557.3
0
139.3
~
~
1
1
1
1 T
K
T
K
T

~ T ~
K2 = T2
K2T
2
⎡ 151300
⎢
⎢
− 60460
⎢ 0
= ⎢
⎢−151300
⎢ − 60460
⎢
⎢⎣
334.7
− 60460
24350
0
60460
− 24350
901.3
0
0
0
0
0
0
−151300
60460
0
151300
− 60460
− 334.7
− 60460
− 24350
0
− 60460
24350
− 836.8
334.7 ⎤
⎥
901.3
⎥
0 ⎥
⎥
− 334.7⎥
− 836.8⎥
⎥
4854 ⎥⎦
Following the relations in the allocation table the following scheme of assembly of the global
stiffness matrix and the global force vector is created.
k 11,1 k 12,1 k 13,1 k 14,1 k 15,1 k 16,1 –R 01,1
k 22,1 k 23,1 k 24,1 k 25,1 k 26,1 –R 02,1
k 33,1 k 34,1 k 35,1 k 36,1 –R 03,1
k 44,1 k 45,1 k 46,1 –R 04,1
k 55,1 k 56,1 –R 05,1
k 66,1 –R 06,1
s y m m e t r y
k 11,2 k 12,2 k 13,2 k 14,2 k 15,2 k 16,2 –R 01,2
k 22,2 k 23,2 k 24,2 k 25,2 k 26,2 –R 02,2
k 33,2 k 34,2 k 35,2 k 36,2 –R 03,2
k 44,2 k 45,2 k 46,2 –R 04,2
s y m m e t r y k 55,2 k 56,2 –R 05,2
k 66,2 –R 06,2
Both the elements contribute simultaneously to the values k 44 , k 45 , k 54 and k 55 in the stiffness matrix
K. The appropriate values from the element stiffness matrices are added in these windows. Due to
the elastic support in the direction of the displacement 9 requires an addition of the spring stiffness
k in the value k 99 of the global stiffness matrix K. The nodal force 20kN acting along the direction 4
in its positive orientation must be added to the element P 4 of the vector P.
Thus the global matrix K and the vector P are formed.
139.3 0 557.3 –139.3 0 0 0 0 0 0 0
143000 0 0 –143000 0 0 0 0 0 0
2229 –557.3 0 0 0 0 0 0 0
151439 –60460 0 0 –151300 60460 334.7 18.707
167350 0 0 60460 –24350 836.8 11.768
0 0 0 0 0 0
0 0 0 0 0
81545 –60460 –334.7 1.2931
s y m m e t r y 24350 –836.8 18.233
4854 –18.750

Now the support conditions must be included. In the analyzed frame the following support
displacements are zero:
q
= q q q q
1 2 = 3 = 8 = 10 =
Thus, the 1 st , 2 nd , 3 rd , 8 th and 10 th elements in the vector P and the elements in the 1 st , 2 nd , 3 rd , 8 th
and 10 th rows and columns of K must be set to zero except for the elements at the diagonal of K,
which are set to 1.
The rotations at the hinge q 6 and q 7 are not zero but were eliminated on the element level by the
static condensation. Thus, they also must be eliminated from the global set of equations. This can
be done by setting the elements k 66 and k 77 at the diagonal of K to 1. Thus the rotations will be kept
in the vector of unknowns and their values will be calculated as 0. Despite the fact, that these
values are not true, they will not be used in further calculations, because they were indeed
eliminated. They will be denoted with asterisks.
Thus we get the final form of the global set of equilibrium equations
0
1 0 0 0 0 0 0 0 0 0 0
1 0 0 0 0 0 0 0 0 0
1 0 0 0 0 0 0 0 0
151439 –60460 0 0 0 60460 0 18.707
167350 0 0 0 –24350 0 11.768
1 0 0 0 0 0
1 0 0 0 0
1 0 0 0
s y m m e t r y 24350 0 18.233
1 0
Solving of the equations
Kq = P
Yields the following vector of global displacements
⎡ 0 ⎤
⎢ ⎥
⎢
0
⎥
⎢ 0 ⎥
⎢ ⎥
⎢0.0001022⎥
⎢0.0001346⎥
q = ⎢ ⎥
⎢ 0 * ⎥
⎢ 0 * ⎥
⎢ ⎥
⎢ 0 ⎥
⎢ ⎥
⎢
0.0001880
⎥
⎢⎣
0 ⎥⎦
Following the relations in the allocation table the appropriate displacements can be attributed to the
elements and the element vectors of displacements in global co-ordinates can be formed.

q
1
⎡q
⎢
⎢
q
⎢q
= ⎢
⎢q
⎢q
⎢
⎢⎣
q
1
2
3
4
5
6
⎤ ⎡ 0 ⎤
⎥ ⎢ ⎥
⎥ ⎢
0
⎥
⎥ ⎢ 0 ⎥
⎥ = ⎢ ⎥
⎥ ⎢0.0001022⎥
⎥ ⎢0.0001346⎥
⎥ ⎢ ⎥
⎥⎦
⎢⎣
0 * ⎥⎦
q
2
⎡q
⎢
⎢
q
⎢q
= ⎢
⎢q
⎢q
⎢
⎢⎣
q
These vectors can be transformed to local co-ordinates
q
~
1 = T1q
1
q
~
2 = T1q
2
to get
⎡ 0 ⎤
⎢
⎥
⎢
0
⎥
⎢ 0 ⎥
q
~
1 = ⎢
⎥
⎢−
0.0001346⎥
⎢ 0.0001022 ⎥
⎢
⎥
⎢⎣
0 * ⎥⎦
1
2
3
4
5
6
⎤ ⎡0.0001022⎤
⎥ ⎢ ⎥
⎥ ⎢
0.0001346
⎥
⎥ ⎢ 0 * ⎥
⎥ = ⎢ ⎥
⎥ ⎢ 0 ⎥
⎥ ⎢0.0001880⎥
⎥ ⎢ ⎥
⎥⎦
⎢⎣
0 * ⎥⎦
⎡ 0.0000449 ⎤
⎢
⎥
⎢
0.0001629
⎥
⎢ 0 * ⎥
q
~
2 = ⎢
⎥
⎢−
0.0000698⎥
⎢ 0.0001746 ⎥
⎢
⎥
⎢⎣
0 ⎥⎦
With these vectors the final values of nodal reactions can be found
~ ~ ~ ~
R +
1 = K1q1
R01
R 2 = K2q2
+ R02
⎡ 19.248 ⎤
⎢ ⎥
⎢
− 0.014
⎥
~ ⎢ − 0.057 ⎥
R 1 = ⎢ ⎥
⎢−19.248⎥
⎢ 0.014 ⎥
⎢ ⎥
⎢⎣
0 ⎥⎦
~
~
~
~
⎡ 25.701 ⎤
⎢ ⎥
⎢
−10.448
⎥
~ ⎢ 0 ⎥
R 2 = ⎢ ⎥
⎢−14.559⎥
⎢−17.407⎥
⎢ ⎥
⎢⎣
18.740 ⎥⎦
Note, that the values of rotations at the hinge denoted by 0* are indeed not necessary, because
they are multiplied by zeros in 6 th or 3 rd column in the stiffness matrices for the element 1 and 2,
respectively.
These reactions can be finally used to find the distributions of the internal forces
–25.7
–
–14.6
10.4
+ –
18.74
N [kN]
– –19.2
+ 0.014
–17.4
T [kN]
M [kNm]
0.057
The correctness of these calculations can be checked by the usual kinematic and static check, as it
was done in the case of classical flexibility and force methods. The only thing, that differs is the
fact, that the present calculations in the matrix version of the stiffness method were carried out with

the released assumption of axial non-deformability of the beams. Hence, the displacement in the
kinematic check must be calculated from the enhanced version of the principle of virtual work (also
including the term due to the elastic support)
(0)
(0)
MM NN R9R
1 ⋅δ
= ∑ ∫ dx + ∑ ∫ dx +
EI EA k
x
x
(0)
9