Fractional reaction-diffusion equation for species ... - ResearchGate

More documents

Recommendations

Info

14 Baeumer, Kovács, Meerschaert Remark 3 Theorem 1 extends immediately to any abstract reaction-diffusion equation of the form (27) as long as u ↦→ [ ˜S(t)](u) is concave down on some interval u ∈ [0, M] for each t > 0, and solutions to the differential equation ˙u = f(u) remain in this interval for all time whenever u(0) ∈ [0, M]. It also extends to the case where f(u, x) depends on the point x in space, and/or the multidimensional case x ∈ R d , since all the proofs are point-wise. Hence the results of this paper can also be adapted to model patchy populations in d-dimensional space, where the growth rate and carrying capacity vary with spatial location. The most familiar choice for the infinitely divisible semigroup T (t) in Theorem 1 is the Gaussian semigroup, where k t is the normal density with mean zero and variance 2Dt for some D > 0. This is the semigroup introduced in Example 1, and since the Lévy representation of k is [0, 2D, 0] (i.e., we have a = 0, φ ≡ 0, and b 2 = 2D in (24)), equation (26) shows that its generator is Au = D ∂ 2 u/∂x 2 . In applications to biology, the probability density k t is the dispersal kernel that describes the dispersion of population over a time interval of length t. The choice of a Gaussian dispersal kernel is justified by the central limit theorem [21,36] which states that the accumulation of a series of independent random movements will converge to a Gaussian form as the number of movements increases to infinity. This is the same argument that justifies the Brownian motion model in cell and molecular biology. There are several reasons why the Gaussian dispersal kernel might not apply as a model for the spread of a population density. First of all, the time interval may be too short for the limit theorem to apply. Second, correlation in movements can invalidate the Gaussian limit. Finally, and most important for the purposes of this paper, heavy tailed movements can also invalidate the Gaussian limit. Recent empirical research [13,16,17,26,28,43,58–60] has produced a body of evidence indicating a power law distributions of movements, so that if R is the magnitude (radius) of the movement of a randomly selected member of the population, then we have P (R > r) ≈ Cr −α for r large. A log-log plot of such movements will exhibit as a straight line with slope −α (power law tail), see for example Figure 2 in [60] or Figure 3 in [58] or Figure 2 in [13]. This leads to a density function k(r) ≈ Cαr −α−1 for r large, and so if 0 < α < 2, then an easy calculation shows that the second moment ∫ r 2 k(r)dr = ∞. The non-existence of the second moment invalidates the Gaussian central limit theorem, and in this case an alternative limit theorem applies [21,36] in which the Gaussian limit distribution is replaced by the more general Lévy stable distribution. The stable probability density function cannot be written in closed form, except in a few special cases, so it is common to describe these distributions in terms of their Fourier transforms ˆk(λ) = e ψ(λ) where ⎧ ⎨ −iaλ − σ α |λ| α (1 − iβ(signλ) tan πα 2 ) for α ≠ 1 ψ(λ) = ⎩ −iaλ − σ|λ|(1 + iβ 2 π (signλ) ln λ) for α = 1 where the stable index 0 < α ≤ 2, the skewness −1 ≤ β ≤ 1, the center a ∈ R, and the scale σ ≥ 0 [49]. The Gaussian distribution is the special
Fractional reaction-diffusion equation 15 case α = 2, and in that case the skewness is superfluous. Stable distributions represent the only possible limits of normalised sums of independent random variables, so they are in some sense universal models for diffusion processes. Stable densities generalise the more familiar Gaussian densities to include the possibility of skewness and heavy power law tails, since for α < 2 the stable density k(y) ≈ Cqα|y| −α−1 as y → −∞ and k(y) ≈ Cpαy −α−1 as y → ∞ where β = p − q. The weights p, q represent the relative chance of large negative versus positive movements, respectively. 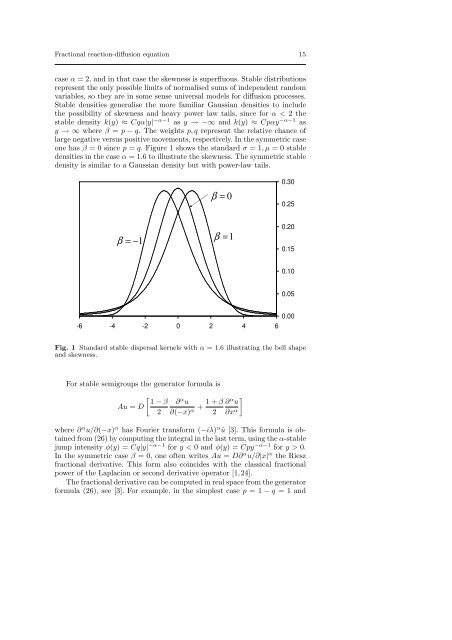In the symmetric case one has β = 0 since p = q. Figure 1 shows the standard σ = 1, µ = 0 stable densities in the case α = 1.6 to illustrate the skewness. The symmetric stable density is similar to a Gaussian density but with power-law tails. β = 0 0.30 0.25 β = −1 β =1 0.20 0.15 0.10 0.05 -6 -4 -2 0 2 4 6 0.00 Fig. 1 Standard stable dispersal kernels with α = 1.6 illustrating the bell shape and skewness. For stable semigroups the generator formula is [ 1 − β ∂ α u Au = D 2 ∂(−x) α + 1 + β ∂ α ] u 2 ∂x α where ∂ α u/∂(−x) α has Fourier transform (−iλ) α û [3]. This formula is obtained from (26) by computing the integral in the last term, using the α-stable jump intensity φ(y) = Cq|y| −α−1 for y < 0 and φ(y) = Cpy −α−1 for y > 0. In the symmetric case β = 0, one often writes Au = D∂ α u/∂|x| α the Riesz fractional derivative. This form also coincides with the classical fractional power of the Laplacian or second derivative operator [1,24]. The fractional derivative can be computed in real space from the generator formula (26), see [3]. For example, in the simplest case p = 1 − q = 1 and
Page 1 and 2: Noname manuscript No. (will be inse
Page 3 and 4: Fractional reaction-diffusion equat
Page 13: Fractional reaction-diffusion equat
Page 21: Fractional reaction-diffusion equat

Fractional reaction-diffusion equation for species ... - ResearchGate

You also want an ePaper? Increase the reach of your titles

Delete template?

Save as template?