3 slides/page - Center for Functional MRI

Bioengineering 280A
Principles of Biomedical Imaging
Fall Quarter 2004
Lecture 5
Sampling
T.T. Liu, BE280A, UCSD Fall 2004
1. Overview of Sampling
2. 1D Sampling
3. 2D Sampling
4. Aliasing
Topics
T.T. Liu, BE280A, UCSD Fall 2004
Analog vs. Digital
The Analog World:
Continuous time/space, continuous valued signals or
images, e.g. vinyl records, photographs, x-ray films.
The Digital World:
Discrete time/space, discrete-valued signals or
images, e.g. CD-Roms, DVDs, digital photos, digital
x-rays, CT, MRI, ultrasound.
T.T. Liu, BE280A, UCSD Fall 2004
1

The Process of Sampling
g(x)
Δx
sample
g[n]=g(n Δx)
T.T. Liu, BE280A, UCSD Fall 2004
Questions
How finely do we need to sample
What happens if we don’t sample finely
enough
Can we reconstruct the original signal or
image from its samples
T.T. Liu, BE280A, UCSD Fall 2004
Sampling in the Time Domain
T.T. Liu, BE280A, UCSD Fall 2004
2

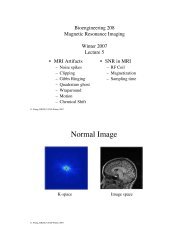
Sampling in Image Space
T.T. Liu, BE280A, UCSD Fall 2004
Sampling in k-space
T.T. Liu, BE280A, UCSD Fall 2004
Sampling in k-space
T.T. Liu, BE280A, UCSD Fall 2004
3

Comb Function
comb(x) = δ(x − n)
∞
∑
n=−∞
€
-5 -4 -3 -2 -1 0 1 2 3 4 5
x
Other names: Impulse train, bed of nails,
shah function.
T.T. Liu, BE280A, UCSD Fall 2004
Scaled Comb Function
⎛
comb
x ⎞
⎜ ⎟ =
⎝ Δx ⎠
∞
∑
n=−∞
δ( x
Δx − n)
∞
= ∑ δ( x − nΔx )
Δx
n=−∞
∞
∑
= Δx δ(x − nΔx)
n=−∞
x
€
Δx
T.T. Liu, BE280A, UCSD Fall 2004
€
T.T. Liu, BE280A, UCSD Fall 2004
1D spatial sampling
g S
(x) = g(x) 1 Δx comb ⎛ x ⎞
⎜ ⎟
⎝ Δx ⎠
Recall the sifting property
∞
∑
= g(x) δ(x − nΔx)
∞
∑
n=−∞
= g(nΔx)δ(x − nΔx)
∞
n=−∞
∞
∫
−∞
g(x)δ(x − a) = g(a)
But we can also write ∫ g(a)δ(x − a) = g(a) ∫ δ(x − a) = g(a)
So, g(x)δ(x − a) = g(a)δ(x − a)
−∞
−∞
∞
€
4

1D spatial sampling
g(x)
comb(x/Δx)/ Δx
x
Δx
g S (x)
x
T.T. Liu, BE280A, UCSD Fall 2004
Fourier Transform of comb(x)
F[ comb(x) ] = comb(k x
)
∞
∑
= δ(k x
− n)
n=−∞
€
⎡
F
1 Δx comb( x
⎣
⎢
Δx ) ⎤
⎦
⎥ = 1
Δx Δxcomb(k xΔx)
∞
∑
= δ(k x
Δx − n)
n=−∞
= 1
Δx
∞
∑
n=−∞
δ(k x
− n Δx )
T.T. Liu, BE280A, UCSD Fall 2004
€
Fourier Transform of comb(x/ Δx)
comb(x/ Δx)/ Δx
Δx
F
x
1/Δx
comb(k x Δx)
1/Δx
k x
T.T. Liu, BE280A, UCSD Fall 2004
5

Fourier Transform of g S (x)
⎡
F[ g S
(x)] = F g(x) 1 Δx comb ⎛ x ⎞ ⎤
⎢
⎜ ⎟ ⎥
⎣
⎝ Δx ⎠ ⎦
⎡
= G(k x
) ∗ F 1 Δx comb ⎛ x ⎞ ⎤
⎢ ⎜ ⎟ ⎥
⎣ ⎝ Δx ⎠ ⎦
= G(k x
) ∗ 1 Δx
= 1 Δx
= 1 Δx
∞
∑
n=−∞
∞
∑
n=−∞
∞
∑
n=−∞
⎛
δ k x
− n ⎞
⎜ ⎟
⎝ Δx ⎠
⎛
G(k x
) ∗δ k x
− n ⎞
⎜ ⎟
⎝ Δx ⎠
⎛
G k x
− n ⎞
⎜ ⎟
⎝ Δx ⎠
T.T. Liu, BE280A, UCSD Fall 2004
€
Fourier Transform of g S (x)
G(k x )
k x
1/Δx
G S (k x )
k x
1/Δx
T.T. Liu, BE280A, UCSD Fall 2004
Nyquist Condition
G(k x )
K S
-B
B
k x
G S (k x )
k x
K S =1/Δx
To avoid overlap, we require that 1/Δx>2B or
K S > 2B where K S =1/ Δx is the sampling frequency
T.T. Liu, BE280A, UCSD Fall 2004
6

Reconstruction from Samples
K S
G S (k x )
K S =1/Δx
Multiply by
(1/K S )rect(k x /K S )
(1/K S ) G S (k x )rect(k x /K S )
=G(k x )
T.T. Liu, BE280A, UCSD Fall 2004
Reconstruction from Samples
If the Nyquist condition is met, then
G ˆ
S
(k x
) = 1 G S
(k x
)rect(k x
/K S
) = G(k x
)
K S
And the signal can be reconstructed by convolving the sample
with a sinc function
€
g ˆ S
(x) = g S
(x) ∗ sinc(K s
x)
∞
= ∑g(nΔX)δ(x −nΔX) ∗sinc(K s
x)
n=−∞
∞
∑
= g(nΔX) sinc(K s
(x − nΔx))
n=−∞
T.T. Liu, BE280A, UCSD Fall 2004
€
Example Cosine Reconstruction
cos(2πk 0 x)
-k 0 k 0
K S >2k 0
-k 0 k 0
K S
K S =2k 0
-k 0
K S
k 0
T.T. Liu, BE280A, UCSD Fall 2004
7

Cosine Example with K S =2k 0
T.T. Liu, BE280A, UCSD Fall 2004
Example with K s =4k 0
T.T. Liu, BE280A, UCSD Fall 2004
Example with K s =8k 0
T.T. Liu, BE280A, UCSD Fall 2004
8

Sine Example with K s =2k 0
T.T. Liu, BE280A, UCSD Fall 2004
Example Sine Reconstruction
-k 0
-k 0
-k 0
K S
2jsin(2πk 0 x)
k 0
K S >2k 0
k 0
K S
K S =2k 0
Aliased!
k 0
T.T. Liu, BE280A, UCSD Fall 2004
Aliasing
-B
G(k x )
k x
B
K S
Aliasing occurs when the Nyquist condition is not satisfied.
This occurs for K S ≤ 2B
T.T. Liu, BE280A, UCSD Fall 2004
9

Aliasing Example
T.T. Liu, BE280A, UCSD Fall 2004
Aliasing Example
cos(2πk 0 x)
-k 0 k 0
K S =k 0
-k 0 k 0
K S
T.T. Liu, BE280A, UCSD Fall 2004
Aliasing Example
cos(2πk 0 x)
-k 0 k 0
2k 0 >K S >k 0
-k 0 k 0
K S
T.T. Liu, BE280A, UCSD Fall 2004
10

Practical Considerations
Why sample higher than the Nyquist frequency
-- true sinc interpolation is not practical since the sinc
function goes from -infinity to infinity
-- the requirements on the low-pass filter are reduced.
Hard
-k 0 k 0
Easier
-k 0 k 0
T.T. Liu, BE280A, UCSD Fall 2004
K S
Fourier Sampling
F
Instead of sampling the
signal, we sample its Fourier
Transform
F -1
Sample
T.T. Liu, BE280A, UCSD Fall 2004
Fourier Sampling
(1 /Δk x ) comb(k x /Δk x )
k x
Δk x
G S
(k x
) = G(k x
) 1 ⎛
comb
k ⎞
x
⎜ ⎟
Δk x ⎝ Δk x ⎠
∞
= G(k x
) ∑δ(
k x
− nΔk x
)
∞
n=−∞
= ∑G(nΔk x
)δ( k x
− nΔk x
)
n=−∞
T.T. Liu, BE280A, UCSD Fall 2004
€
11

Fourier Sampling -- Inverse Transform
Χ =
*
1/Δk x
Δk x
=
T.T. Liu, BE280A, UCSD Fall 2004
Fourier Sampling -- Inverse Transform
g S
(x) = F −1 [ G S
(k x
)]
⎡
= F −1 G(k x
) 1 ⎛
comb
k ⎞ ⎤
x
⎢
⎜ ⎟ ⎥
⎣ Δk x ⎝ Δk x ⎠ ⎦
⎡
= F −1 [ G(k x
)] ∗ F 1 ⎛
−1 comb
k ⎞ ⎤
x
⎢ ⎜ ⎟ ⎥
⎣ Δk x ⎝ Δk x ⎠ ⎦
= g(x) ∗comb( xΔk x )
∞
= g(x) ∗ ∑δ(xΔk x
− n)
n=−∞
= g(x) ∗ 1
Δk x
= 1
Δk x
∞
∑
n=−∞
g(x
∞
∑
n=−∞
δ(x
− n
Δk x
)
− n
Δk x
)
T.T. Liu, BE280A, UCSD Fall 2004
€
Nyquist Condition
FOV (Field of View)
1/Δk x
To avoid overlap, 1/Δk x > FOV, or equivalently, Δk x

Aliasing
FOV (Field of View)
1/Δk x
Aliasing occurs when 1/Δk x < FOV
T.T. Liu, BE280A, UCSD Fall 2004
Aliasing Example
Δk x =1
1/Δk x =1
T.T. Liu, BE280A, UCSD Fall 2004
2D Comb Function
∞
comb(x,y) = δ(x − m,y − n)
∞
∑ ∑
m=−∞ n=−∞
∞ ∞
∑ ∑
= δ(x − m)δ(y − n)
m=−∞ n=−∞
= comb(x)comb(y)
€
T.T. Liu, BE280A, UCSD Fall 2004
13

Scaled 2D Comb Function
comb(x /Δx, y /Δy) = comb(x /Δx)comb(y /Δy)
∞
∞
∑ ∑
= ΔxΔy δ(x − mΔx)δ(y − nΔy)
m=−∞ n=−∞
€
Δy
T.T. Liu, BE280A, UCSD Fall 2004
Δx
* =
1/∆k
X =
T.T. Liu, BE280A, UCSD Fall 2004
2D k-space sampling
1 ⎛
G S
(k x
,k y
) = G(k x
,k y
) comb
k x
, k ⎞
y
Δk x
Δk
⎜
y ⎝ Δk x
Δk
⎟
y ⎠
∞
∞
= G(k x
,k y
) ∑ ∑δ(
k x
− mΔk x
,k y
− nΔk y
)
∞
∞
m=−∞ n=−∞
= ∑ ∑G(mΔk x
,nΔk y
)δ( k x
− mΔk x
,k y
− nΔk y
)
m=−∞ n=−∞
€
T.T. Liu, BE280A, UCSD Fall 2004
14

2D k-space sampling
[ ]
g S
(x, y) = F −1 G S
(k x
,k y
)
⎡
1 ⎛
= F −1 G(k x
,k y
) comb
k x
, k ⎞ ⎤
y
⎢
Δk x
Δk
⎜
y ⎝ Δk x
Δk
⎟ ⎥
⎣ ⎢
y ⎠ ⎦ ⎥
⎡
1 ⎛
= F −1 [ G(k x
,k y
)] ∗ F −1 comb
k x
, k ⎞ ⎤
y
⎢
Δk x
Δk
⎜
y ⎝ Δk x
Δk
⎟ ⎥
⎣ ⎢
y ⎠ ⎦ ⎥
= g(x, y) ∗∗comb( xΔk x )comb( yΔk y )
∞ ∞
= g(x) ∗∗ ∑ ∑δ(xΔk x
− m) δ(yΔk y
− n)
m=−∞
n=−∞
∞
1
= g(x) ∗∗ ∑
Δk x
Δk y m=−∞
∞ ∞
1
= ∑ ∑g(x
Δk x
Δk y
m=−∞
n=−∞
∞
∑
n=−∞
δ(x
− m
Δk x
)δ(y − n
Δk y
)
− m
Δk x
, y − n
Δk y
)
T.T. Liu, BE280A, UCSD Fall 2004
€
Nyquist Conditions
FOV X
1/∆k Y > FOV Y
1/∆k X > FOV X
1/∆k Y
FOV Y
1/∆k X
T.T. Liu, BE280A, UCSD Fall 2004
Aliasing
T.T. Liu, BE280A, UCSD Fall 2004
15