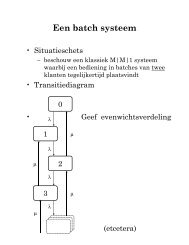
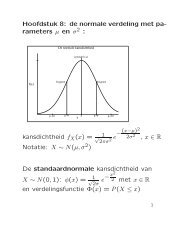
Advanced Queueing Theory

Advanced Queueing Theory 

1 

• Networks of queues 

(reversibility, output theorem, tandem networks, partial 

balance, product-form distribution, blocking, insensitivity, 

BCMP networks, mean-value analysis, Norton's theorem, 

sojourn times) 

• Analytical-numerical techniques 

(matrix-analytical methods, compensation method, error 

bound method, approximate decomposition method) 

• Polling systems 

(cycle times, queue lengths, waiting times, conservation 

laws, service policies, visit orders) 

Richard J. Boucherie 

department of Applied Mathematics 

University of Twente 

http://wwwhome.math.utwente.nl/~boucherierj/onderwijs/Advanced Queueing Theory/AQT.html

Last time on AQT … 

2 

• Output reversible queue 

• Tandem network of queues 

• Jackson network 

• Kelly Whittle network 

• Partial balance 

• Blocking


Today (lecture 3): queue length based on Kelly’s 

lemma 

Nelson, sec 10.4—10.7, Kelly, chapter 3 

3 


• Alternative proof 

• Quasi reversibility 

• Network of quasi reversible queues 

• Queue disciplines, symmetric queues, BCMP networks 

• PASTA 

• Mean Value Analysis

Kelly Whittle network 

4 

Theorem: The equilibrium distribution for the Kelly Whittle 

network is 

where 

and π satisfies partial balance

Insert equilibrium distribution and rates in partial balance 

5 

This is the beauty of partial balance! 

rate in = rate out



lemma 


6 






• PASTA 


Time reversed process 

7 

• Theorem: If X(t) is a stationary Markov process with transition 

rates q(j,k), and equilibrium distribution π(j), j ∈ S, then the 

reversed process X( τ - t) is a stationary Markov process with 

transition rates 

and the same equilibrium distribution. 

€ 

• Theorem: Kelly’s lemma 

Let X(t) be a stationary Markov process with transition rates 

q(j,k). If we can find a collection of numbers q’(j,k) such that 

q’(j)=q(j), j ∈S, and a collection of positive numbers π(j), 

j ∈ S, 

summing to unity, such that 

€ 

€ 

then q’(j,k) are the transition rates of the time-reversed process, 

and (j), j S, is the equilibrium distribution of both processes. 

π ∈ € €

Alternative proof: use Kelly’s lemma 

8 

Forward rates 

Guess 

backward rates 

Check conditions

Alternative proof: use Kelly’s lemma 

9 

Guess for equilibrium distribution 

insert



lemma 


10 






• PASTA 


Quasi-reversibility 

• Multi class queueing network, class c 

• A queue is quasi-reversible if its state x(t) is a stationary 

Markov process with the property that the state of the queue 

at time t 0 , x(t 0 ), is independent € of 

(i) arrival times of class c customers subsequent to time t 0 

(ii) departure times of class c customers prior to time t 0 . 

∈ 

C 

• Theorem 

If a queue is QR then 

(i) arrival times of class c customers form independent 

Poisson processes 

(ii) departure times of class c customers form independent 

Poisson processes.


• S(c,x) set of states queue contains one more class c 

customer than in state x 

• Arrival rate class c customer 

independent of state x 

• Thus arrival rate independent of prior events, and has 

constant rate Poisson proces


• Multi class queueing network, class c 

• S(c,x) set of states in which queue contains one more 

class c than in state x 

• Arrival rate class c customer 


€ 

• Departure rate class c customer 


∈ 

C 

• Characterise QR, combine 

• Partial balance



lemma 


14 






• PASTA 


Network of quasi reversible queues 

• Multiclass queueing network, type i=1,..,I 

• J queues 

• Customer type identifies route 

• Poisson arrival rate per type (i), i=1,…,I 

• Route r(i,1),r(i,2),…,r(i,S(i)) 

• Type i at stage s in queue r(i,s) 

• S(c,x) set of states in which queue contains one more class c 

than in state x 

15 

• State X(t)=(x 1 (t),…,x J (t)) 

• Fixed number of visits; cannot use Markov routing 

• 1, 2, or 3 visits to queue: use 3 types

Network of quasi reversible queues 

16 

• Construct network by multiplying rates for individual queues 

• Transition rates 

• Arrival of type i causes queue k=r(i,1) to change at 

• Departure type i from queue j = r(i,S(i)) 

• Routing 

• Internal

• Rates 

Network of Quasi-reversible queues 

• Theorem : For an open network of QR queues 

(i) the states of individual queues are independent at fixed time 

(ii) an arriving customer sees the equilibrium distribution 

(ii’) the equibrium distribution for a queue is as it would be in 

isolation with arrivals forming a Poisson process. 

(iii) time-reversal: another open network of QR queues 

(iv) system is QR, so departures form Poisson process


• Proof of part (i): Kelly’s lemma 

• Rates 

• Transition rates reversed process (guess)


• Proof of part (i): Kelly’s lemma 

• For 

• We have 

• Satisfied due to



lemma 


20 






• PASTA 


Queue disciplines 

• Operation of the queue j: 

(i) Each job requires exponential(1) amount of service. 

(ii) Total service effort supplied at rate ϕ j (n j ) 

(iii) Proportion γ j (k,n j ) of this effort directed to job in 

position k, k=1,…, n j ; when this job leaves, his service is 

completed, jobs in positions k+1,…, n j move to positions k,…, 

n j -1. 

(iv) When a job arrives at queue j he moves into position k 

with probability j (k,n j + 1), 

k=1,…, n j +1; jobs previously in positions k,…, n j move to 

positions k+1,…, n j +1.

Queue disciplines 




(iii) Proportion j (k,n j ) of this effort directed to job in position 

k, 

(iv) job arriving at queue j moves into position k with prob. 

j (k,n j + 1) 

• In the form of network of quasi reversible queues 

• Examples: BCMP network 

FCFS 

LCFS 

PS 

infinite server queue,

Symmetric queues 




(iii) Proportion j (k,n j ) of this effort directed to job in position 

k, 

(iv) job arriving at queue j moves into position k with prob. 

j (k,n j + 1) 

• Examples: IS, LCFS, PS 

• Symmetric queue QR for general service requirement 

• Instantaneous attention 

• Symmetric queue is insensitive

Quasi-reversibility and partial balance 

• QR: fairly general queues, service disciplines, Markov 

routing, product form equilibrium distribution 

factorizes over queues. 

• PB: fairly general relation between service rate at 

queues, state-dependent routing (blocking), product 

form equilibrium distribution factorizes over service 

and routing parts. 

• Identical for single type queueing network with 

Markov routing 

• QR partial balance 

• NOT partial balance QR (exercise) 

• NOT QR Reversibility (see Nelson, ex 10.14) 

• NOT Reversibility QR (see Nelson, ex 10.12)



lemma 


25 






• PASTA 


Arrival theorem 

• PASTA: 

The distribution of the number of customers in the system seen by a 

a customer arriving to a system according to a Poisson process (i.e., 

at an arrival epoch) equals the distribution of the number of 

customers at an arbitrary epoch. 

• Arrival theorem (open Jackson network): 

In an open network in equilibrium, a customer arriving to queue j 

observes the equilibrium distribution. 

• Arrival theorem (closed Jackson network): 

In a closed networkin equilibrium, a customer arriving to queue j 

observes the equilibrium distribution of the network containing one 

customer less.

PASTA: Poisson Arrivals See Time Averages   

27 

• fraction of time system in state n 

• probability outside observer sees n customers at time t 

• probability that arriving customer sees n customers at time t 

(just before arrival at time t there are n customers in the system) 

• in general

28 


• Let C(t,t+h) event customer arrives in (t,t+h) 

• For Poisson arrivals q(n,n+1)= so that 

• Alternative explanation; PASTA holds in general!

29 


• Transient 

• In equilibrium

30 

MUSTA: Moving Units See Time Averages   

• Palm probabilities:   

Each type of transition nnʼ for Markov chain associated with subset H of SxS \diag(SxS) 

• Example:transition in which customer queue i queue j 

H ij 

= 

• Transition in which customer leaves queue i 

H 

i 

out 

{(m + e i 

,m + e j 

),m + e i 

,m + e j 

∈ S} 

m 

= 

H ij 

j 

• Transition in which customer enters queue j 

H in j 

= 

H ij 

i

31 

MUSTA: Moving Units See Time Averages   

• N H process counting the H-transitions 

• Palm probability P H (C) of event C given that H occurs:   

P H 

(C) = 

∑(n,n')∈C 

π(n)q(n,n') 

∑ π(n)q(n,n') , C ⊆ H 

(n,n')∈ H 

• Probability customer queue i queue j sees state m 

P ij 

(m) = P H ij 

((m + e i 

,m + e j 

)) = π(m + e )q(m + e ,m + e ) 

i i j 

, 

π(n)q(n,n') 

∑(n,n')∈ H ij 

• Probability customer arriving to queue j sees state m 

P j 

(m) = P H j 

in ( 

(m + e i 

,m + e j 

)) = 

i 

∑ π(m + e 

i 

i 

)q(m + e i 

,m + e j 

) 

∑ 

i 

∑ π(n)q(n,n') , 

(n,n')∈ H ij

Kelly Whittle network 

32 

Theorem: The equilibrium distribution for the Kelly Whittle 

network is 

where 

and π satisfies partial balance

MUSTA :Kelly Whittle network 

33 

Theorem: The distribution seen by a customer 

moving from queue i tot queue j is 

Entering queue j is 

where

MUSTA   

34



lemma 


35 






• PASTA 


Gesloten netwerken: MVA 

Average queue length, average sojourn times 

λ m (i) arrival intensity queue i, 

F m (i) expeceted sojourn time i, 

L m (i) expected queue length queue i, when m cust in system 

Arrival theorem, FCFS 

Little’s formula

Gesloten netwerken: MVA 

λ m (i) arrival intensity queue i, 

F m (i) expeceted sojourn time i, 

L m (i) expected queue length queue i, when m cust in system 

€ 

€ 

• Little 

• thus 

λ m 

(i) = 

N 

∑ 

j=1 

λ m 

( j) ⋅ r ji 

€ 

π i 

= 

λ m 

(i) = λ m 

⋅ π i 

, λ m 

= λ m 

(i) 

N 

∑ 

i=1 

⎧ 

λ m 

= m ⋅ ⎨ 

⎩ 

N 

∑ 

i=1 

N 

∑ π j 

⋅ r ji 

, ∑ π i 

=1 

j=1 

⎫ 

π i 

⋅ F m 

(i) ⎬ 

⎭ 

−1 

N 

i=1

• Mean Value Analysis 

evaluates λ m (i), F m (i) en L m (i) for all m,i recursively 

– Find solution π of traffic equations 

– for m=1 : F 1 (i)=1/µ i for all i 

recursion 

– let F m (i) known for all i 

– Determine number of cust served per time unit at queue i : 

λ m 

(i) = λ m 

⋅ π i 

= m ⋅ 

{ ∑ 

N 

π 

j=1 j 

⋅ F m 

( j) } −1 ⋅ π i 

– Determine average number of customers at queue i 

using Little 

– Determine average sojourn time at queue i for system 

€ containing m+1 customers using arrival theorem 

F m +1 

(i) = 1+ L m(i) 

µ i 

€ 

L m 

(i) = λ m 

(i) ⋅ F m 

(i)

Exercises 

Exercises from Kelly, Reversibility and stochastic networks: 1.5.2, 1.6.4, 2.2.4, 2.3.5, 2.4.1, 3.1.3, 3.1.4, 3.2.3 

Exercise on blocking: Consider a Jackson network of J queues with transition rates 

1. Give the equilibrium distribution, and show that this distribution satisfies partial balance 

2. Show that a customer arriving to queue i observes the equilibrium distribution 

3. Now assume that the total number of customer in the network is restricted not to exceed N. Give the 

equilibrium distribution, and the distribution of the state observed by a customer arriving to queue 1 

4. Now assume that each queue has a capacity restriction, say the number in queue i is restricted not to exceed Ni. 

Consider the stop protocol, where the arrival process, and each non-blocked queue is stopped until a service 

completion has occurred at the blocked queue. Give the state space, and show that the equilibrium distribution 

has a product form and satisfies partial balance. Give the distribution of the state observed by a customer 

arriving to (and entering) queue 1. 

5. Again assume the capacity restrictions of 4). Assume that a customer arriving to a queue that has reached its 

capacity restriction, say queue j, jumps over the queue, and selects a new destination according to the routing 

probilities from queue j. Give the equilibrium distribution. 

6. Can the product form result of 4) be obtained via Quasi reversibility If so, provide the proof of the product form 

result via quasi reversibility. 

Exercise on insensitivity: Consider a BCMP network consisting of infinite server queues, and single server queues, 

where the single server queues may be FCFS, LCFS or PS. Assume Markov routing. 

1. Formule the BCMP network as a network of quasi reversible queues. 

2. Give the equilibrium distribution. 

3. Show that this distribution satisfies partial balance. 

4. Restrict the network to contain IS, LCFS, and PS queues only (symmetric queues). Prove that the equilibrium 

is insensitive to the distibution of the service time at each of these queues using first the phase type 

distribution approach, and then the formulation of Whittle. 

5. Indicate why the distribution cannot be insensitive to the service time distribution in an FCFS queue.

Advanced Queueing Theory

Create successful ePaper yourself

Delete template?

Save as template?