Advanced Queueing Theory - Department of Computer Science ...

Advanced Queueing Theory
1
• Networks of queues
(reversibility, output theorem, tandem networks, partial
balance, product-form distribution, blocking, insensitivity,
BCMP networks, mean-value analysis, Norton's theorem,
sojourn times)
• Analytical-numerical techniques
(matrix-analytical methods, compensation method, error
bound method, approximate decomposition method)
• Polling systems
(cycle times, queue lengths, waiting times, conservation
laws, service policies, visit orders)
Richard J. Boucherie
department of Applied Mathematics
University of Twente
http://wwwhome.math.utwente.nl/~boucherierj/onderwijs/Advanced Queueing Theory/AQT.html

2
• Doe na de m/m/1 eerst even de M/E_r/1 expliciet uit
notes
• Laat dan expliciet zien dat generator een blok structuur
heeft
• Ga dan pas naar QBD

Advanced Queueing Theory
Today (lecture 7): Matrix analytical techniques
3
• G. Latouche, V Ramaswami. Introduction to Matrix Analytic
Methods in Stochastic Modeling, SIAM, Philadelphia, 1999
• Tutorial on Matrix analytic methods:
http://www-net.cs.umass.edu/pe2002/papers/nelson.pdf
• M/M/1 queue
• Quasi birth death process
• Generalisations

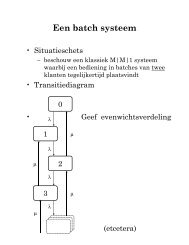
M/M/1 queue
4
• Poisson arrival process rate ,
single server, exponential service times, mean 1/
• State space S={0,1,2,…}
• transition rates :
• Global balance
• Detailed balance
• Equilibrium distribution

0 =
5

Advanced Queueing Theory
Today (lecture 7): Matrix analytical techniques
7
• G. Latouche, V Ramaswami. Introduction to Matrix Analytic
Methods in Stochastic Modeling, SIAM, Philadelphia, 1999
• Tutorial on Matrix analytic methods:
http://www-net.cs.umass.edu/pe2002/papers/nelson.pdf
• M/M/1 queue
• Quasi birth death process
• Generalisations

8
Vector state process: example M/E_k/1
• Let service requirement in single server queue be Erlang (k,apple)
• Augment state description with phase of Erlang distribution
• State (n,j): n= # customers, j = #remaining phases
• Transitions
(n,j)(n+1,j) arrival (rate apple)
(n,j)(n,j-1) completion of phase (j>1) (rate apple)
(n,j)(n-1,k) completion in last phase, dept (n>1,j=1) (rate apple)
(n,j)(0) completion for n=1, (j=1) (rate apple)
(0)(1,k) arrival to empty system (rate apple)
• Picture
• Generator in block structure
• M/Ph/1

Phase and level
9

10
Quasi-birth-death process (QBD)
Q i blocks of size M x M

π i blocks of size M
12

Theorem: equilibrium distribution
13

14
Stability
Behaviour in phase direction
x stat distrib
over phases
downward drift

15
QBD: Proof of equilibrium distribution
For the discrete time case, R(i,j) is the expected number of
visits to phase j in level 1 before absorption in level 0
for the process that starts at level 0 in phase i

Proof, ctd
18

19
Computing R
• For computation of R, rearrange
• Note that Q 1 is indeed invertible, since it is a
transient generator
• Fixed point equation solved by successive
substitution
• It can be shown that

20
Example: E k /M/1 queue
• Let service requirement in single server queue be Exp(apple)
• Let interarrival time be Erlang (k, apple)
• Augment state description with phase of Erlang distribution
• State (n,j): n=# customers, j =#remaining phases
• Transitions
(n,1)(n+1,k) arrival (rate apple)
(n,j)(n,j-1) completion of phase (j>1) (rate apple)
(n,j)(n-1,j) service completion (n>1) (rate apple)
• Picture
• Generator in block structure

Advanced Queueing Theory
Today (lecture 7): Matrix analytical techniques
21
• G. Latouche, V Ramaswami. Introduction to Matrix Analytic
Methods in Stochastic Modeling, SIAM, Philadelphia, 1999
• Tutorial on Matrix analytic methods:
http://www-net.cs.umass.edu/pe2002/papers/nelson.pdf
• M/M/1 queue
• Quasi birth death process
• Generalisations

Generalisations: different first row
22

24
Generalisations: GI/M/1-type Markov chains
• Consider GI/M/1 at arrival epochs
• Interarrival time has general distribution F A with mean 1/
apple
Service time exponential with rate apple
• Probability exactly n customers served during intarr time
• Probability more than n served during intarr time

Generalisations: GI/M/1-type Markov chains
25
• Prob n cust served during intarr time
• Prob more than n served during intarr time
• Transition probability matrix
• Equilibrium probabilities
• Where is unique root in (0,1) of
where A has distribution F A

26
Generalisations: GI/M/1-type Markov chains
• Markov chain with transition matrix (suitably ordered
states) of the form
is called Markov chain of the GI/M/1 type

27
Generalisations: GI/M/1-type Markov chains
• Equilibrium distribution
• Where R is minimal non-negative solution of
• Computation: truncate
• And use successive approximation

28
Generalisations: M/G/1 type Markov chains
• Embedding of M/Q/1 at departure epochs gives upper
triangular structure for transition matrix

29
Generalisations: Level dependent rates
• For Markov chain of the GI/M/1 type, we may generalise
to allow for level dependent matrices, i.e.
A i (n) at level n, i=0,1,2,…, n=0,1,2,…

30
References and Exercise
• http://www.ms.unimelb.edu.au/~pgt/Stochworkshop2004.pdf
• http://www.ms.unimelb.edu.au/~pgt/Stochworkshop2004-2.pdf
• Exercise: Consider the Ph/Ph/1 queue. Formulate as
Matrix Analytic queue (i.e. specify the transition matrix, and
the blocks in that matrix). For the E 2 /E 2 /1 queue, obtain
explicit expression for R, and give the equilibrium distribution