Linear Differential Game With Two Pursuers and One Evader

*
( μ
1H
11
− ε
1H
21
) + ε
1H
21( v2
1
1)
*
( μ H − ε H ) + ε H ( v 1)
z1 f
= z1
+
x
+
2 f
= z
2
−
2 12 2 22 2 22 2x1
−
z
From which, using the initial equality, we can isolated
the evader bounds) :
v
*
2×
1
( z)
=
*
v
2x1
(subject to saturation if
2
( − μ H − z ) τ + ( μ H − z )
1
ε
11
2
H
1
22
τ
P1
2
P2
+ ε
2 12 2
2
1
H
21
τ
P1
τ
2
P2
*
v
2x1
is higher than
*
v
2x1
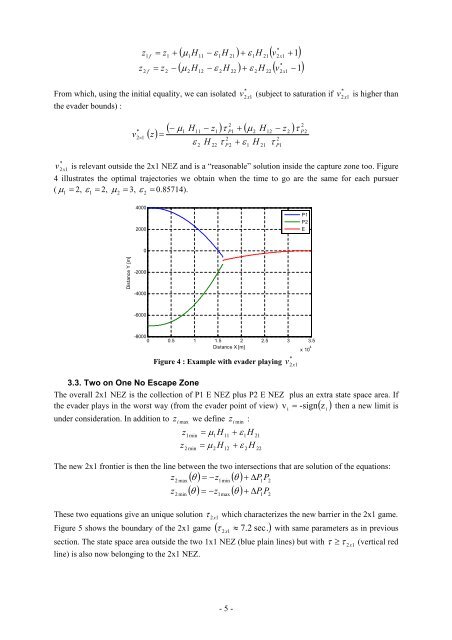
is relevant outside the 2x1 NEZ and is a “reasonable” solution inside the capture zone too. Figure
4 illustrates the optimal trajectories we obtain when the time to go are the same for each pursuer
( μ1
= 2, ε1
= 2, μ2
= 3, ε
2
= 0.85714).
4000
2000
P1
P2
E
0
Distance Y [m]
-2000
-4000
-6000
-8000
0 0.5 1 1.5 2 2.5 3 3.5
Distance X [m]
x 10 4
Figure 4 : Example with evader playing
*
v
2x1
3.3. Two on One No Escape Zone
The overall 2x1 NEZ is the collection of P1 E NEZ plus P2 E NEZ plus an extra state space area. If
the evader plays in the worst way (from the evader point of view) vi = -sign( z
i
) then a new limit is
under consideration. In addition to z
i max
we define z
i min
:
z1min
= μ
1H11
+ ε
1H
21
z = μ H + ε
2 min 2 12 2H
22
The new 2x1 frontier is then the line between the two intersections that are solution of the equations:
z θ = −z
θ + ΔP
z
( )
1min
( )
1 2
( θ ) = −z1max
( θ ) + ΔP1
2
2 max
P
2 min
P
These two equations give an unique solution τ
2x1
which characterizes the new barrier in the 2x1 game.
Figure 5 shows the boundary of the 2x1 game ( τ
2x1
≈ 7.2 sec. ) with same parameters as in previous
section. The state space area outside the two 1x1 NEZ (blue plain lines) but with τ ≥ τ 2x 1
(vertical red
line) is also now belonging to the 2x1 NEZ.
- 5 -