Method of images (note2)

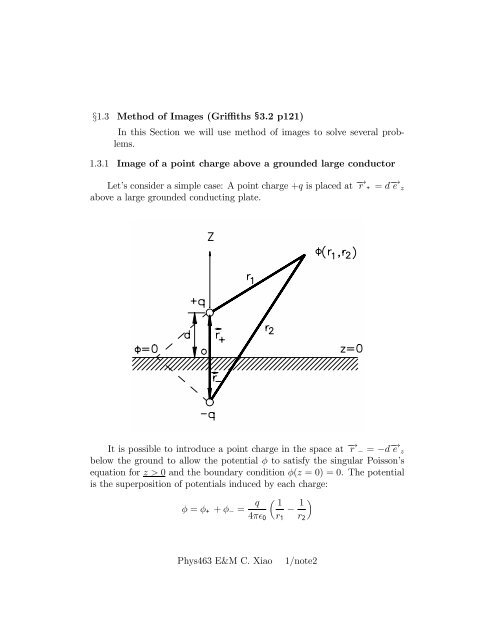
§1.3 Method of Images (Griffiths §3.2 p121)In this Section we will use method of images to solve several problems.1.3.1 Image of a point charge above a grounded large conductorLet’s consider a simple case: A point charge +q is placed at −→ r + = d −→ e zabove a large grounded conducting plate.It is possible to introduce a point charge in the space at −→ r − = −d −→ e zbelow the ground to allow the potential φ to satisfy the singular Poisson’sequation for z>0 and the boundary condition φ(z = 0) = 0. The potentialis the superposition of potentials induced by each charge:φ = φ + + φ − =q µ 1− 1 4π² 0 r 1 r 2Phys463 E&M C. Xiao1/note2

The Poisson’s equation has singularity at −→ r + and −→ r − .Inthetophalfspace:∇ 2 φ = − q ² 0δ( −→ r − −→ r + ) − q ² 0δ( −→ r − −→ r − )= − q ² 0δ( −→ r − −→ r + ) z>0Note: : The effect of the image charge is equivalent to that of the surfacecharge induced on the conducting plate. The image charge must be OUTSIDEthe region under consideration.Apparently, the induced negative charge on the surface is now replacedby an image charge to allow φ = 0 at the boundary z =0.The solution is unique according to the uniqueness theorem.Note: the solution is valid only in the space z>0.The charge density induced on the surface:D 1n − D 2n = ε 0 (E 1n − E|{z} 2n )=σ,=0σ = ε 0 E 1n = −ε 0∂φ∂zthe explicit expression for φ is⎛⎞φ =q1⎝q 4πε 0 x2 + y 2 +(z − d) − 1q ⎠2 x2 + y 2 +(z + d) 2Ãqz − dσ = ε 04πε 0 (x 2 + y 2 +(z − d) 2 ) 3/2= − 12πz + d−(x 2 + y 2 +(z + d) 2 )!¯¯¯¯¯z=03/2qd(x 2 + y 2 + d 2 ) 3/2The total charge on the surface is q surface = −qThe force on the +q charge isF = 14πε 0q 2(2d) 2Phys463 E&M C. Xiao2/note2

same as the force between the +q charge and the image charge −q with aseparation of 2d.The Energy of the system isW = − 14πε 0q 24drather than W = − 14πε 0q 22das (G2.36) suggested (read the text on page 123 to see why).1.3.2 Potential due to a Charge Placed Above a Dielectric BodyAssume the permittivity of the dielectric body is ² and the boundary isthe x-y plane at z =0• ImagesFor z>0 (in the air), image charge −q 0 at −→ r − = −d −→ e z :φ + = 1 Ã ! q− q04π² 0 r 1 r 2Phys463 E&M C. Xiao3/note2

∇ 2 φ + = − q δ( −→ r − −→ r + )+ q0δ( −→ r − −→ r − )² 0 ² 0= − q δ( −→ r − −→ r + ) z>0² 0For z

Now,D z+ = −² 0∂φ +∂z¯¯z=0,D z− = −² ∂φ −∂z¯¯z=0D z+ = D z− leads tod4π(x 2 + y 2 + d 2 ) (−q − d3/2 q0 )=−4π(x 2 + y 2 + d 2 q00)3/2This gives the second equationq 00 = q + q 0(B)Solve the equation system (A) and (B) for q 0 and q 00q 0 = ² − ² 0² + ² 0q, q 00 = 2²² + ² 0q• Electric FieldsIn the half space above z = 0, the electric field is bent due to thenegative image charge. In the half space below z = 0 the electricfield lines are straight and radially outward from the centre at the +qlocation.Phys463 E&M C. Xiao5/note2

1.3.3 Image for a Sphere (See Griffiths §3.2.4, p124)Consider a charge +q at a distance D from a grounded (solid) conductingsphere of radius a. The potential is symmetric about the line connecting thecentre and the charge. The image charge −q 0shouldbeonthesamelineatadistancex from the centre.Phys463 E&M C. Xiao6/note2

• PotentialPotential at point A and B on the sphere should vanishOrφ A =φ B =Ratioofthetwoequations14π² 0Ã qD − a −Ã1 q4π² 0 D + a −qD − a =qD + a =q0a − xq0a + xD − aD + a = a − xa + xq0!=0a − x!q0a + x=0Phys463 E&M C. Xiao7/note2

Solve for x from the above equation and then solve for q 0 :x = a2D ,q0 = a D qSoφ(r, θ) =q à 1−a !4π² 0 r + Dr −Using the laws of cosine:r>ar + = √ D 2 + r 2 − 2rD cos θr − = √ x 2 + r 2 − 2xr cos θvuà t a =2 ! 2+ rD2 − 2 a2D r cos θAt r = ar − | r=a =vuà t a 2 ! 2+ aD2 − 2 a2D a cos θ= a D√a2 + D 2 − 2aD cos θ = a D r +| r=aThis verifies that the potential vanishes on the spherical surfaceφ(a, θ) =q à !1 a− =04π² 0 r + | r=a Dr − | r=a• Surface charge densityInside the sphere −→ D =0. Soσ = D r = ² 0 E r∂φσ(θ) = −² 0 ¯∂r ¯r=a⎡= − q² 0⎣− r − D cos θ + r − a2 cos θ⎤Da⎦4π² 0 r+3 r−3 ¯D¯r=aPhys463 E&M C. Xiao8/note2

⎡= − q ⎢⎣− a − D cos θ + a − a2D cos θ4π (r + | r=a ) 3= q4π=Ã1a − D2(r + | r=a ) 3 a³(r + | r=a ) 3 aD!(a 2 − D 2 )q4πa(D 2 + a 2 − 2aD cos θ) 3/2´3⎤a ⎥⎦DThe total charge residing on the surface of the sphere isas expected.q S =Z π0σ(θ) · 2πa 2 sin θdθ= 1 2 (a2 − D 2 )aq= − a D q = −q0Z 1dµ−1 (a 2 + D 2 − 2aDµ) 3/2| {z }=2D(D 2 −a 2 )Phys463 E&M C. Xiao9/note2