Light-Front Holography and Novel Collider Physics

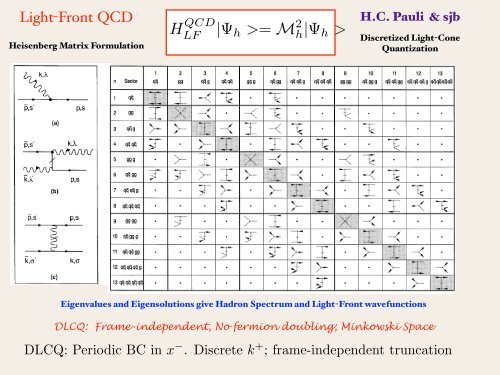
More generally, consider a meson in SU(N). The kernel of the integral equation (3.14) isLight-Front illustrated QCDin Fig. 2 in terms of the block matrix nS.J. Brodsky et LC al. / Physics h =Reports 2 : x , k , λ Hn : x, h 301 H.C. k , λ . Pauli The structure & sjbof thismatrix depends of course H QCD on the way one has arranged the Fock space, see Eq. (3.7). Note that most(1998) h h>of the block matrix elements LF |Ψ h >= M 2vanish due to the natureh|Ψof the h >light-cone 299—486 Discretized interaction Light-Cone as defined inHeisenberg Matrix FormulationQuantizationEigenvalues and Eigensolutions give Hadron Spectrum and Light-Front wavefunctionsFig. 2. The Hamiltonian matrix for a SU(N)-meson. The matrix elements are represented by energy diagrams. Withineach block they are all of the same type: either vertex, fork or seagull diagrams. Zero matrices are denoted by a dot ( ) ).The single gluon is absent since it cannot be color neutral.Fig. 6. A few selected matrix elements of the QCD front form Hamiltonian H"P in LB-convention.DLCQ: Frame-independent, No fermion doubling; Minkowski Spaceor the DLCQ: instantaneous Periodic BC fermion in xlines − . Discrete use the factor k + ; frame-independent ¼ Fig. 5 or Fig. truncation 6, or the correspoables in Section 4. For the instantaneous boson lines use the factor ¼ .