Shopping Externalities and Self Fulfilling Unemployment Fluctuations*

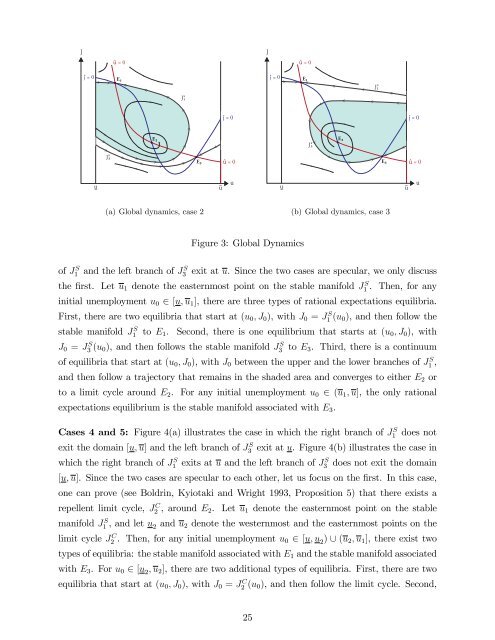
JJů = 0ů = 0E1E1J1sJ1sE2J3sE2J3sE3ů = 0E3ů = 0uu(a) Global dynamics, case 2(b) Global dynamics, case 3Figure 3: Global Dynamicsof J1 S and the left branch of J3 S exit at u. Since the two cases are specular, we only discussthe …rst. Let u 1 denote the easternmost point on the stable manifold J1 S . Then, for anyinitial unemployment u 0 2 [u; u 1 ], there are three types of rational expectations equilibria.First, there are two equilibria that start at (u 0 ; J 0 ), with J 0 = J1 S (u 0 ), and then follow thestable manifold J1 S to E 1 . Second, there is one equilibrium that starts at (u 0 ; J 0 ), withJ 0 = J3 S (u 0 ), and then follows the stable manifold J3S to E 3 . Third, there is a continuumof equilibria that start at (u 0 ; J 0 ), with J 0 between the upper and the lower branches of J1 S ,and then follow a trajectory that remains in the shaded area and converges to either E 2 orto a limit cycle around E 2 . For any initial unemployment u 0 2 (u 1 ; u], the only rationalexpectations equilibrium is the stable manifold associated with E 3 .Cases 4 and 5: Figure 4(a) illustrates the case in which the right branch of J1S does notexit the domain [u; u] and the left branch of J3S exit at u. Figure 4(b) illustrates the case inwhich the right branch of J1 S exits at u and the left branch of J3 S does not exit the domain[u; u]. Since the two cases are specular to each other, let us focus on the …rst. In this case,one can prove (see Boldrin, Kyiotaki and Wright 1993, Proposition 5) that there exists arepellent limit cycle, J2 C , around E 2 . Let u 1 denote the easternmost point on the stablemanifold J1 S , and let u 2 and u 2 denote the westernmost and the easternmost points on thelimit cycle J2 C . Then, for any initial unemployment u 0 2 [u; u 2 ) [ (u 2 ; u 1 ], there exist twotypes of equilibria: the stable manifold associated with E 1 and the stable manifold associatedwith E 3 . For u 0 2 [u 2 ; u 2 ], there are two additional types of equilibria. First, there are twoequilibria that start at (u 0 ; J 0 ), with J 0 = J2 C (u 0 ), and then follow the limit cycle. Second,25